基于改进EOQ模型的进料批量控制的研究

聂景峰，李立红

（1.山西太钢不锈钢股份有限公司炼钢二厂，山西 太原 030001；2.北京科技大学，北京 100083）

0 引言

利润最大化是每个企业的最终目标。要想获得更大的利润，企业应该对生产的各个环节追求精益求精，从而尽可能地降低成本或增加收入。进料作为金属冶炼企业生产的必要环节，其进料批量的大小直接关系着企业的经济效益，然而大多数企业往往对该环节不够重视，仅仅是以满足生产需要为目的并根据人为经验来进行进料。因此通过建立数学模型并科学的求解最优进料批量对于提高企业生产效益有重要意义。经济订货批量模型是在一定的理想化条件下通过定量的分析总费用从而确定最优订货批量，受限于一定的理想化条件该模型的应用范围得到限制。本文将在传统经济订货批量模型的基础上，结合进料的实际情况进行改进建立进料批量数学模型，这对于金属冶炼企业的进料环节具有借鉴与指导意义。

1 现状及存在问题

某金属公司冶炼某种钢材需要不同数量的多种金属原料，为保证生产的连续性与均衡性，该公司需要提前进来一定数量的原料进行储备，在进料量一定时，进料批量过多不仅会增加存储成本，而且存储量过多时可能会导致原料受损，从而造成浪费。而进料批量过少又可能导致厂家短期内无法满足生产的需要，影响生产的连续性，造成停产损失，甚至厂家因无法按期交货需支付购方赔偿。因此，在进料时间已知的情况下，确定一个合理的进料量，对于提高公司的经济收益有重要意义[1]。

目前，该公司采用的进料批量确定方法为根据往常进料经验进行人为进料批量的确定。具体方法为：在已知进料时间的前提下，根据月订单量确定每周不同原料的需求量，以每周为单位进行进料。该种方法下的进料周期（该种原料的一个进料周期为两次进料间隔的时期）及进料批量没有经过科学的计算，也未考虑在进料过程中的一些限制因素，给进料过程带来了麻烦并造成了一部分不必要的成本损耗。为提高进料的效率与经济收益，本文从进料总成本最小的角度出发，综合考虑运输、存储与生产过程的限制因素，建立进料批量数学模型，通过求解函数从而可以得到最优的进料批量。

2 进料批量数学模型的建立与求解

以该公司生产一种钢材所需要的一种原料进行进料批量模型建立并求解。

2.1 假设条件

（1）该公司一个进料周期内对该种钢材的需求量服从正态分布。（2）订料的费用与订料的多少无关。（3）运料的费用与运输量成正比例。（4）该种原料的最大库存为无限大。（5）该种原料只作为该种钢材的成分使用，不作其他用途。（6）进料的提前期为已知常量。

2.2 变量表示[2]

2.3 模型建立

已知该公司每月份该种钢材的生产量为D0，该种钢材所含该种原料的有效成分比例为α，该种原料的收得率为β，则该种原料的月需求量为：

该种原料在进料周期内的使用量服从均值为Q（可根据下文所建数学模型求解得到）、尺度参数为σ（大小取决于实际生产）的概率分布，其概率密度函数为正态分布为

图1 原料使用量的概率密度函数

为满足一定的服务水平，需使原料库存满足生产需求的概率η大于一定值，一般取0.95，因此可以得出在原料库存满足生产需求的概率为0.95时的安全库存[3]为

该种原料一个月内的持有费用为

其中安全库存的持有费用

该种原料一个月内的运输费用为

该种原料一个月内的订料费用为

所以一个月内的总费用为

H、σ、α、β、S、T0、D0均为已知量。

2.4 模型求解

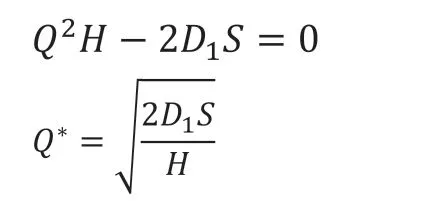
此时的Q为最优解，此时总费用最小

在总进料量一定的情况下，随着进料批量的不同，各个费用的变化图2所示，从图中可以看出，随着Q的增大，订料费用单向递减，持有费用单向递增，运输费用为总运输量的函数始终为定值，通过计算可得当订料费用与持有费用相等时，此时总费用最小，此时得到的进料批量为最优进料批量[4]。

图2 不同进料批量下的费用

3 模型可行性分析

本文假设进料批量模型前提条件为该原料的使用速率为一定值，但在实际生产过程中，由于受天气、工人生产积极性、意外因素等的影响，该原料的使用率为变量，因此需要讨论在这种情况下该模型是否仍然适用。

同时，本文假设了该原料的最大库存量为无限大，但在实际生产过程中，这种现象并不存在，因此，需要讨论在最大库存量为定值的情况下进料批量的确定策略。

（1）原料的实际消耗量为变值。因为实际情况中原料的使用速率并非恒定，因此实际情况与建立的数学模型有一定误差，如下图。

图3 实际进货与理想进货的对比

从上图可以看到，实际的用料量可能比预期的少或多，而理想预期为原料使用率为一定值，实际情况比理想情况更加复杂，因此模型建立并非准确，但是由于该模型合理设计了安全库存，通过调整η可保证所需要的生产原料需求率，且该模型建立简单，易于求解，所以模型可以在满足实际生产的需求求得最优的进料量[5]。

（2）最大库存的限制。前文假设该种原料的库存量没有限制，但实际情况中，库房的大小是有限制的，因此进料量受限于库存量，此时的调整策略为如下：根据最大库存量以及现有库存计算出最大进料批量Q1（Q1'），根据上述模型计算出最优进料量Q2，从图中可以看出，若Q2小于Q1（Q1'），取进货批量为Q2，若Q2大于Q1（Q1'），取进货量为Q1（Q1'），此时进料次数大于最优进料批量下的进料次数，具体进料量如图4所示。有最大库存量限制的不同进料批量下的费用图5所示。

图4 有库存限制时的进料批量

图5 不同进料批量下的费用

4 模型评价与改进

本文借鉴经济批量订货模型EOQ的最优订货量的确定方法，建立了某种原料的进料批量模型，通过使得运输费用、持有费用以及订料费用之和最小，求解出最优进料批量。对比传统的根据人为经验确定进料量的方法，本文建立的进料批量模型不仅减小了总的费用，提高了该企业的经济效益，同时减少了库存量的堆放，一定程度上减少了产品的浪费。相比于传统的EOQ模型，本文不仅增加了安全库存量的设置及确定方法，可避免因库存不足造成停产等现象的发生，而且考虑了实际生产过程中可能遇到的原料使用速率的不确定及最大库存的限制等现实因素，并给出了相应的解决方法。

5 结语

总之，该模型也有一定的不足之处，比如该模型简化了生产的过程，没有考虑实际生产中的钢材需求量、交货期的改变，从而引起的原料需求量的改变。同时，本文也没有考虑停产成本，因此模型计算出的最优进料量与实际最优进料量间存在误差。因此，若想将获得更精准的进料批量还需要结合实际生产情况进一步增加变量从而优化模型。