直接液力式智能完井超长距离液压传递特性研究*
张 亮 刘景超 杨建义 盛磊祥 李瑞丰
(1. 中海油能源发展股份有限公司工程技术分公司 天津 300452; 2. 中海油研究总院有限责任公司 北京 100028)
智能完井技术可以采集井下温度、压力等参数,通过地面控制系统对目标层位流量控制阀开度闭环控制,实现监测油层生产动态及油藏优化智能开采的目的。智能完井技术涉及地面控制、井下测量、可调开度的井下流量控制阀等技术,由于系统能够对多层和多分支井进行分层地面遥测遥控,因此对油层生产数据的测量更精确,油井管理也更为科学[1]。
目前,智能完井主要采用液压驱动的井下流量控制系统[2],而直接液力式智能完井因其系统简单、可靠性高和成本较低的优点,成为智能完井液压驱动井下流量的主要控制方式[3]。直接液力驱动智能完井是通过液控管线将液力直接作用在流量控制阀上,从而直接推动液压缸活塞。由于井下流量控制阀位置较深且未安装位置传感器,需要通过对进油、回油管线中的流量和流速监测实现井下流量控制阀的定位,所以直接液力式智能完井系统需要解决超长距离液压传递沿程压力损失、温度对液压油运动黏度的影响及井下流量控制阀精准定位等问题。
本文以达西公式和液阻、液感和液容等效理论为基础,研究长距离液压传递的特性,探讨等效平均流量及控制阀动作响应时间,为智能完井井下流量控制阀精准定位提供支持。
1 直接液力式智能完井液压传递的主要技术难题
流体在传输过程中是层流和紊流2种混合状态,其传输特性受环境温度、系统压力及管道形状、类型的影响较大。流体本身具有黏性,流体和管壁之间的碰撞或摩擦会对流体自身的流动产生阻力,克服这种阻力主要表现为压力损失。因而,直接液力式智能完井液压传递需要解决以下3个技术难题。
1) 井下流量控制阀的定位通过流量和流速进行判定,流量控制阀执行器的容积较小,管线受到压力作用也会发生容积变化,因次,容积变化如何对系统产生影响是第1个技术难题。
2) 流量控制阀入井位置一般大于1 000 m,如何解决长距离液压传输沿程压力损失和作业时效是第2个难题。
3) 随着井深的增加,液压油的运动黏度受温度影响很大,井温变化如何对液压传递产生影响是第3个难题。
2 液压传递特性理论分析
2.1 长距离传递沿程压力损失
通常情况下液控管线的内径较小,在进油过程中由于其流量较小,因而可认为液压油在液控管线中的流动近似层流。对于非等温不锈钢液控管线层流,其液压油的管路沿程阻力系数λ可表示为
(1)
式(1)中:λ为管路沿程阻力系数,无量纲;ρ为液压油的密度,kg/m3;v为液体的平均流速,m/s;d为液控管线内径,m;μ为液压油动力黏度,Pa·s;ν为运动黏度,mm2/s。
液压油在管线中流动的压力损失Δp可由达西公式表达为[4]
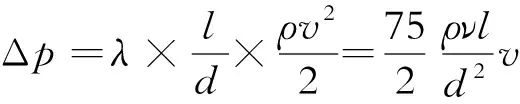
(2)
式(2)中:l为液控管线长度,m。
由式(2)可以看出,沿程压力损失和液压油运动黏度、密度及液控管线类型及流体运动速度有关。当压力损失Δp为定值时,如果液控管线所处的环境温度相同,则液压油的运动黏度相同,液压油的流速可表达为
(3)
2.2 井温对液压传递的影响
直井的井温t与垂深h的近似线性关系可表达为
(4)
式(4)中:t为井温,℃;h为垂深,m;C0为地温梯度,℃/100 m;t0为地表气温,℃。
液压油运动黏度与温度之间的关系复杂,当液压油温度为30~150 ℃、40 ℃运动黏度小于135 mm2/s时,不同温度液压油的运动黏度可表达为[5]
(5)
式(5)中:ν40为液压油40 ℃的运动黏度,mm2/s;n为指数,其大小随液压油40 ℃运动黏度而改变。
2.3 液压传递的特性函数
综合式(1)~(5),以井的垂深为自变量,可以得到瞬时流量的连续函数为
(6)
式(6)中:Q为瞬时流量,L/min;k为定向井计算校正系数。
根据等效理论,式(6)对于确定的管线压力、液压油型号、管线类型和长度,瞬时流量只与井深相关。由于瞬时流量与井深的函数是连续的,利用定积分中值定理可计算等效平均流量为
(7)
式(7)中:Q′为等效平均流量,L/min;H为井深,m。
2.4 液容等效理论分析
流体在管道中的流动情况与电流在电路中的流动情况极为相似,因此流体管道系统可以用等效电路来代替,并按电路的计算法则求解其动态特性[6]。液控管线液容的产生原理是流体的可压缩性及管道产生了变形,对于某一种流体或管道材料而言,表现为固有的弹性模量。在液压系统中,液压油受压时被压缩的体积越大,则液容值也越大[7]。圆形液控管线的液容C为[8]
(8)
式(8)中:C为圆形液控管线的液容,m4·s2/kg;Ep和Ef分别为液控管线和流体的弹性模量,MPa。
根据式(8)可得到液控管线的液容,井下流量控制阀每级开度总体积即为流量控制阀液压缸体积与液控管线液容之和。
2.5 液压传递时间特性
对于确定的液控管线类型、长度及驱动压力,通过井下流量控制阀每级开度总体积和等效平均流量,就可计算得到每级开度的动作时间:
(9)
式(9)中:V为液控管线液容与流量控制阀液压缸的总体积,L;T为流量控制阀动作时间,min。
3 智能完井系统液压传递特性的试验井分析和验证
3.1 试验井智能完井生产管柱
陆地试验井(简称陆试井)为钻采试验基地JJSY-1的直井,流量控制阀下入井深850 m处。试验时用泥浆泵建立水循环模拟系统,液控管线所处的环境温度相同。海上试验井(简称海试井)为恩平18-1油田的定向井,完井井深2 120 m,流量控制阀液控管线长度1 300 m,温度梯度4.18 ℃/100 m。陆试井和海试井智能完井生产管柱图如图1所示。
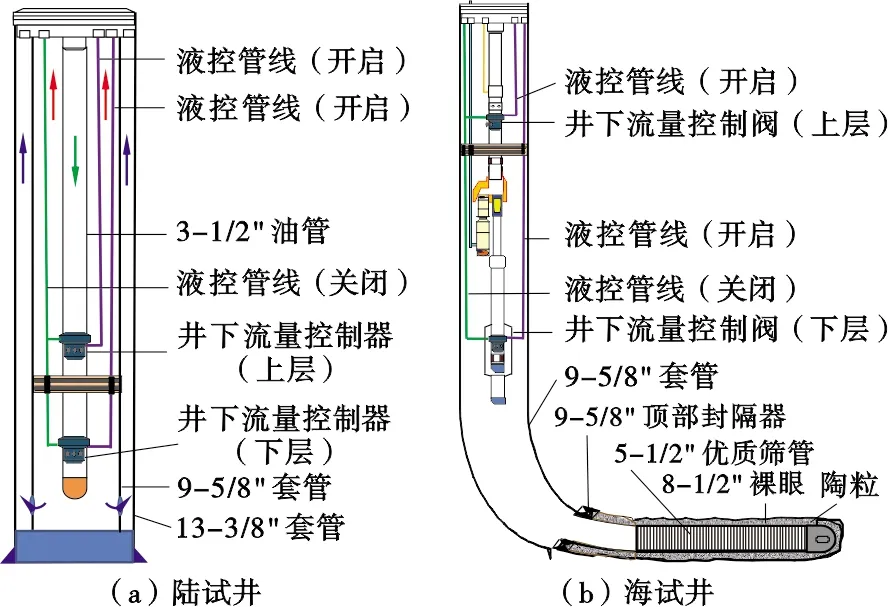
图1 陆试井和海试井智能完井生产管柱图Fig .1 Well completion string diagram for onshore test well and offshore test well
3.2 瞬时流量与井深关系曲线
在试验时,陆试井和海试井的地面控制器输出压力均为35 MPa。陆试井流量控制阀的液控管线温度与水温一致,为11 ℃,通过液压油黏温曲线可得其运动黏度为155 mm2/s。通过式(3)得到其等效平均流量为0.030 7 L/min。海试井由于井温上升较快,其液压油运动黏度的变化导致流体传输瞬时速度的改变。通过式(7)得到其等效平均流量为0.107 2 L/min。陆试井和海试井瞬时流量与井深曲线如图2所示。
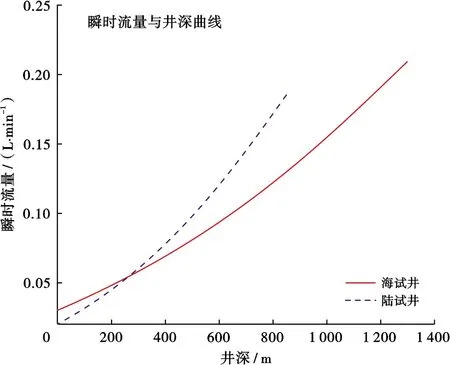
图2 陆试井和海试井瞬时流量与井深曲线Fig .2 Relationship between instantaneous flow and well depth for onshore test well and offshore test well
图2表明,在同一井深条件下,海试井的液控管线瞬时流量较大。这一现象是由于海试井所在海域的地表气温和地温梯度比陆上试验井高而产生的。
对于定向海试井,影响液压传递的主要因素在于井斜阶段,因而在计算整段管线流动时,应对井斜段进行修正。在地面控制器中,高压流量计和低压流量计分别监测液控管线中的进油和回油流速。由于回油流速是基本不变,所以井下流量控制阀的运动可看作匀速运动,其动作时间可采用等效平均流量计算。
3.3 流量控制阀动作时间分析
对于海试井和试验井,其井下流量控制阀的控制响应时间、流量控制阀定位与理论计算基本一致(表1),证明了井下流量控制阀的定位可以通过监测油量和流量实现,同时也证明了通过等效平均流量理论计算井下流量控制阀动作时间,可以作为井下流量控制阀精准定位的辅助判定条件。

表1 流量控制阀动作理论计算时间和试验时间对比Table 1 Interval control valve action time comparison between calculation and test
3.4 智能完井系统的智能控制验证
3.4.1陆试井现场测试
2019年3月,智能完井系统在东沽陆试井进行了现场测试,通过试验井13-3/8″套管、9-5/8″套管及液控智能完井管柱形成的2层环空模拟2个储层段,开泵循环排量为0.8 m3/min,泥浆泵效率为0.8。通过循环系统压耗计算,发现开泵循环压力的理论值与实测值基本一致(图3),验证了陆试井地面控制器对流量控制阀的定位和精准控制。

图3 陆试井开泵循环压力理论计算与实测对比Fig .3 pump operation cycle pressure comparison between theoretical calculation and well test of onshore test well
3.4.2海试井现场测试
2019年6月,智能完井系统在恩平18-1油田某井开展海试。测试时关闭井口采油通道,对智能流量控制阀进行全关、一级、二级、三级等不同开度的调节测试,电潜泵出口与进口的压力差即可反映井下流量控制阀的执行动作,测试结果见图4。可以看出,随着流量控制阀开度的增大,电潜泵出口与进口的压力差逐渐减少,再次关闭后恢复初始压差值。也就是说对于海试井,地面控制器能够驱动中下流量控制阀执行相应的动作指令,完成对流量控制阀的定位和精准控制。

图4 海试井实测流量控制阀开度状态与电潜泵压力差对应关系Fig .4 Relationship between ICV opening conditions and submersible pump pressure difference
4 结论
1) 直接液力式智能完井通过超长液控管线对较小容积活塞缸的驱动,以油量和流量作为判定条件实现了对井下流量控制阀精准判定。
2) 以达西公式和液阻、液感和液容等效理论为基础,通过计算等效平均流量,进而计算出井下流量控制阀液压缸动作时间的方法可以作为流量控制阀精准定位的辅助条件。
3) 等效平均流量方法进一步提高了对井下流量控制阀精准判定水平,为实现井下流量控制阀实时监测、动态调节全自动化控制奠定基础。

