耦合非线性薛定谔方程在凝聚体中的应用
杨晓红,连高社
(太原工业学院理学系,山西太原 030008)
玻色-爱因斯坦凝聚是近些年来物理学领域中的一个研究热点[1-4],具有非常重要的研究意义和应用价值。当原子被冷却到一个临界温度以下时,理想Bose 子气体将会发生相变,导致一种新的物质状态,这种变相称为玻色-爱因斯坦凝聚(Bose-Einstein condensate,简写BEC)。而处于这种新状态的物质被称为玻色-爱因斯坦凝聚体(Bose-Einstein condensates,缩写为BECs)。
用平均场理论处理非均匀玻色-爱因斯坦凝聚系统的基本方程为[5]:

这就是著名的GP方程。其中φ()表示宏观波函数,是m玻色原子质量,g为耦合常数,与s波散射长度as相关。as可正可负,正代表两体相互作用为排斥,负表示两体相互作用为吸引。在实验中s波散射长度的大小和正负都可以利用费施巴赫共振(Feshbach)技术来调节。
对于两个相互作用的凝聚体使用零温的平均场理论,因此可忽略凝聚态原子间的碰撞和热云,则这个凝聚态系统的宏观动力学由两个耦合的GP方程来描述。考虑(1+1)维的情况,对方程进行无量纲处理,耦合方程可以写为[5]:

此时外部简谐势为:
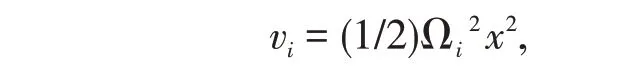
gij为非线性相互作用系数。
已经有很多方法被提出来求解(2),比如F展开法、函数展开法、相似变换法以及Hirota方法等等。
当允许散射长度和外部势阱为随时间变化的函数,不忽略原子间的热云时,则必然导致凝聚体中原子的增益或损耗。因此当处理双组分的玻色-爱因斯坦凝聚体时,应在二耦合的GP方程中包含两个不同的增益或损耗项。则上述方程(2)写成如下形式[6]:

G1(t)、G2(t)分别代表波函数ψ1、ψ2的增益或损耗。当Gi(t)>0,表示凝聚体波函数中热云的损耗;反之当Gi(t)<0,则表示为增益。gij(t)表示相互作用强度,vi(t) 表示外部简势。当g11(t)=g21(t),g12(t)=g22(t),g11(t)=-g12(t),时,用Lax 对和规范变换可求出方程的孤子解。
当自旋自由度被释放,这种带有自旋自由度的玻色气体,被称为旋量玻色气体。首先,通过双线性方法求得二耦合变系数薛定谔方程的孤子解,并利用Maple[7]对孤子解作图。最后,发现调节凝聚体稳定性的各种方法。
1 模型
考虑87Rb原子由两种超精细态组成的旋量玻色-爱因斯坦凝聚,这种凝聚体通过抛物势阱被限制,同时被随时间变化的耦合场耦合。假设凝聚体是一维的,在平均场近似理论下,这个系统可以被变系数二耦合非线性薛定谔方程描述[8]

在方程(4)中ψ1,ψ2分别是旋量凝聚体的波函数,a(t)表示短暂的散射长度,λ(t)和v(t)分别表示两个凝聚体之间的阱频率和耦合,G(t)表示凝聚体热云的增益或(损耗)。
2 分析
根据可积条件[8]:

根据Hirota双线性变换[9-12]构造变换:

式中,g(x,t),h(x,t) 都是复函数,而是f(x,t)实函数。对构造变换的(5)式分别求出ψ1t,ψ1xx,ψ2t,ψ2xx,代入方程(4)式并根据可积条件进行整理,分析得出如下双线性形式:

其中Dt,Dx是双线性算子,有如下形式的微分算子:

其中,p(x,t)是变量x与t的可微函数,是b(x′,t′)变量x′与t′的可微函数,m和n是非负整数;式(7)称为函数p与b对施行m次Dx,又对t施行n次的双线性导数。基于表达式(6),方程组(4)的孤子解可由以下展开式得到:

ε是参量,gi和hi(i=1,3,5,…)是x和t的复函数,fj(j=2,4,6,…)是x和t的实函数。把(8)式代入双线性形式(6)式中,令ε的同幂次项系数为零,得到如下双线性形式:

其中,θ(x,t)=k(t)x+w(t),A,B为复数,k(t)为实函数,w(t)为复函数。
当ε=1 时,(10a),(10b),(10c)代入(9a),(9b),(9c)中可知:

则耦合非线性薛定谔方程的孤子解为:

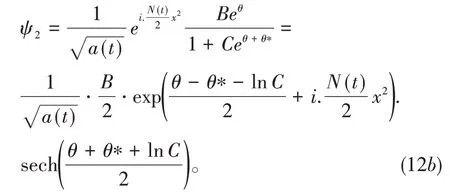
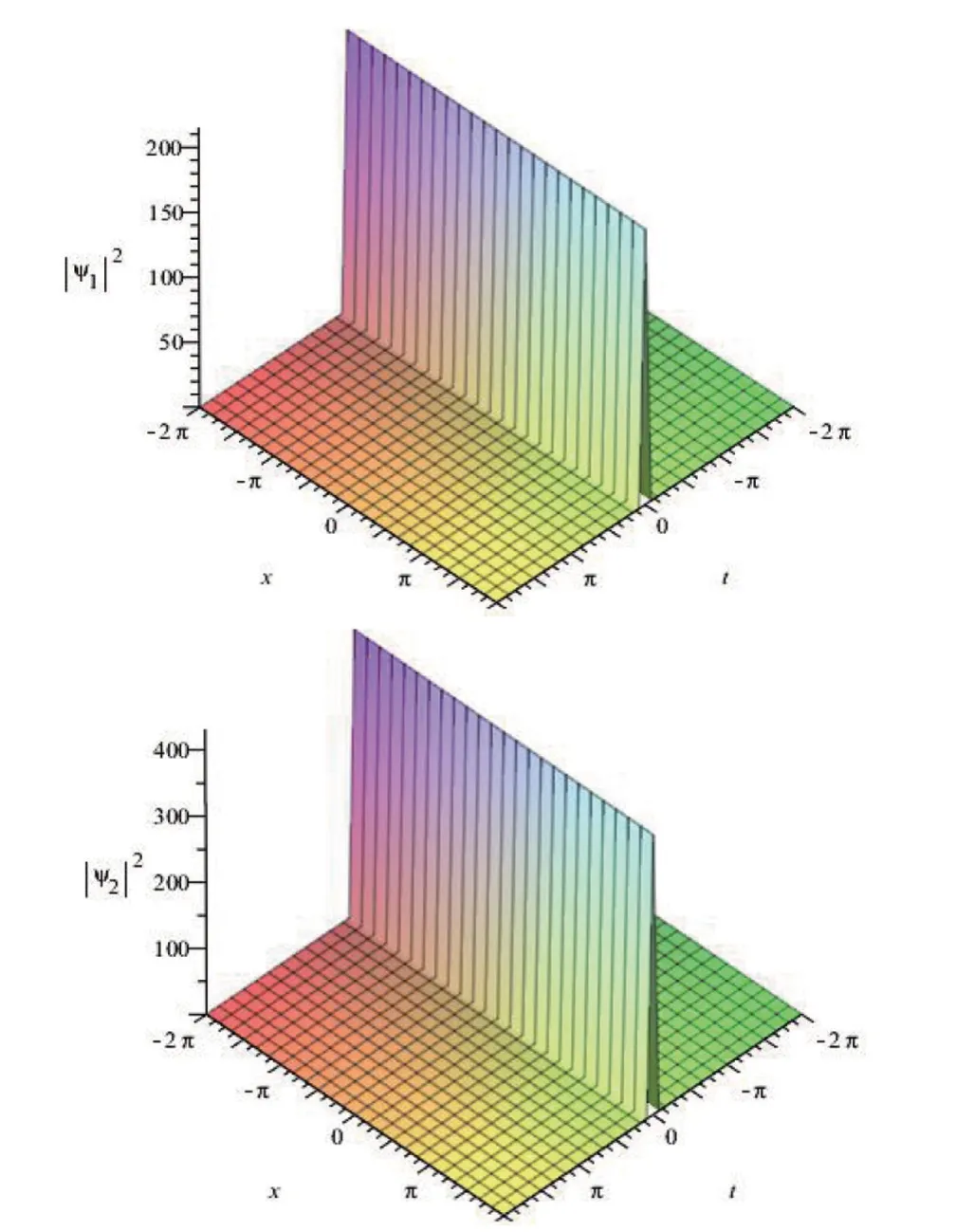
图1 孤子解ψ1,2的演化图像

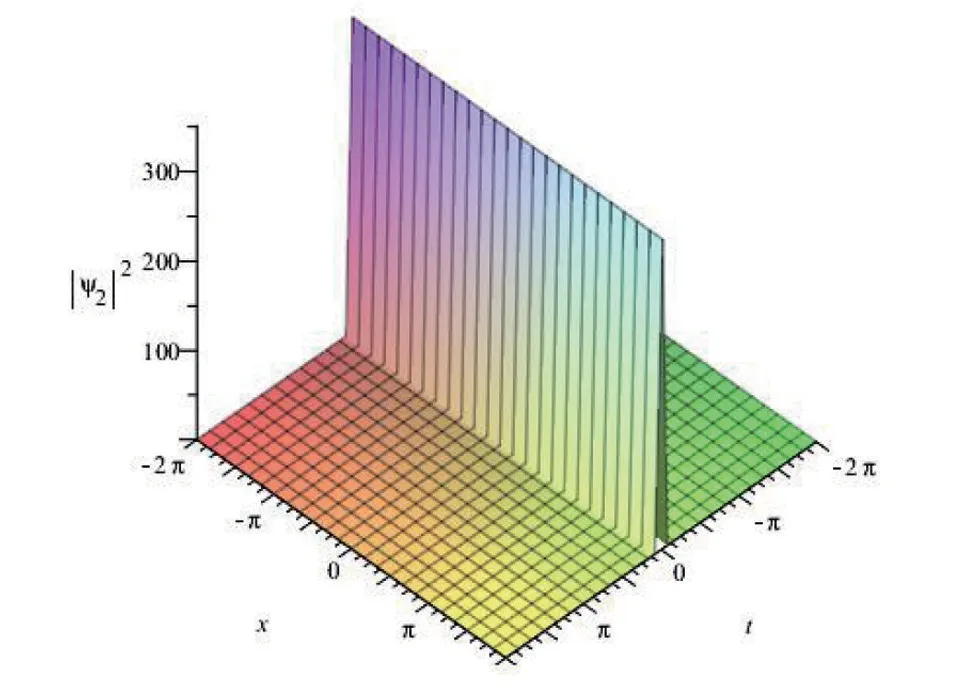
图2 孤子解ψ1,2的演化图像

图3 孤子解ψ1,2的演化图像
凝聚体的稳定特性跟凝聚体中的原子间相互作用以及外部囚禁势阱对原子的作用直接相关。所以,可以通过控制特征参量的值来控制孤子的传输特性与稳定性。经作图发现克服不稳定性既可以通过改变任意函数F(t)(与图1相比较)如图2;也可以通过改变耦合系数v(t)(与图1 相比较)如图3;或者可以调节散射长度a(t)(与图1 相比较)如图4;研究克服凝聚体不稳定性的各种方法为实现量子信息传输提供一定的理论依据同时增大了其作为量子信息载体的可能性。

图4 孤子解ψ1,2的演化图像
3 结语
还可进一步研究得出耦合方程的二孤子解、三孤子解等并分析二、三孤子的传输特性和稳定性。

