基于模糊ANP-熵权法和灰色关联的航海类高校实验室评价

王志平， 王慧闯， 王沛文

（大连海事大学a.理学院；b.航运经济与管理学院，辽宁大连116026）

0 引 言

党的十九大报告提出“坚持陆海统筹，加快建设海洋强国”的发展战略。为了适应国家经济发展的需要，航运人才培养的重任就交到了航海类高校的肩上。为了更好地提高学生的专业知识，满足行业的要求，高校必须提供高质量、高水平、高层次的实验室供学生开展实验教学，科学研究等工作。无论从航海类高校教学需要还是从社会所需人才的角度，实践和创新能力的培养在人才培养中都十分重要。为了提高学校教学质量和办学水平，促进实验室建设与发展，提升实验室建设水平显得极其重要。实验室评价是高校实验室建设与管理的一项重要工作，对于优化高校的资源配置、提升高校实验室建设水平具有重要促进作用，因此实验室评价工作引起广大实验室工作者的重视［1-2］。

在高校实验室评价实施的过程中，建立科学有效的评价指标体系来评估实验室的质量显得尤为重要。越来越多的学者针对实验室评价方法展开了研究。王世浩等［3］采用网络层次分析法建立了实验室过程安全的评价指标体系。李丽［4］提出将三角模糊数和层次分析法相结合建立三角模糊层次分析法的实验室评估模型。阳富强等［5］提出利用网络层次分析法（ANP）和解释结构模型（ISM）相结合建立高校实验室消防安全管理模型。李浩等［6］针对目前现存问题，提出了基于熵权模糊物元模型的财经类高校实验室综合评估方法。田夏［7］提出了通过层次分析法和熵权法相结合，进而建立教学实验室评价体系。吴立荣等［8］提出采用模糊综合评价法对高校实验室进行安全评价。刘晶晶等［9］针对目前实验室的管理所存在的问题，提出利用改进的最有最劣法（BWM）和隶属度理论来构建高校化学实验室安全管理评价模型。

综上所述，学者们进行了多方面的研究，但目前实验室评价中还存在很多问题：①大多数学者在确定指标权重时采用层次分析法或熵权法。层次分析法受主观因素较大，没能考虑到指标之间的相互影响关系。熵权法则是客观性较强，没有体现出决策者的经验及主观意见；②由于决策者间的意见模糊且无法定量分析，难以确定判断矩阵，还缺乏考虑指标之间的相互关系。基于此，本文从多个方面构建航海类高校实验室评价的指标体系，并利用网络分析法和三角模糊数相结合的基于比较判断矩阵的模糊网络层次分析法确定主观权重，利用熵权法确定客观权重，并将二者组合加权得到指标的综合权重，避免了单独选用某种赋权方法可能存在的偏差，使权重的计算更加合理，并采用灰色加权关联分析法对方案进行综合评价，最后通过实例证明综合两种权重方法的评价结果更科学合理。

1 航海类高校实验室评价指标体系构建

指标体系的构建是对实验室评价的最基本的步骤，合理的指标体系将决定评价结果的真实性与准确性。因此在构建指标体系时要遵循科学性、导向性、针对性、易操作性等原则。通过多方查阅文献、实地调研、专家访谈等多种形式，并结合航海类高校人才培养模式的特点以及教学实验室的现状和新特性，总结高院多年来在实验室评估工作中的经验［10-13］，建立以环境安全、仪器设备、师资保障、实验教学作为1级评价指标，各项2级指标具体见表1。

表1 实验室评价指标体系

航海类高校是具有航运背景的高校，除了具有一般高校的共性以外，还有自己的独特性。一般类高校实验室都是分开运营与管理，很难实现资源共享，导致仪器设备重复购置，使用率不高等缺陷，因此在评价指标体系中加入仪器设备共享指标，从而实现信息共享，资源统筹等，即本文构建的评价指标体系中结合航海类高校的独特性，具体分为12个2级指标。

2 模糊语言术语及相关知识

定义1［14］假设~c=（c1，c2，c3）是R中任意的一个三角模糊数，三角模糊数的模糊集对应的隶属度函数定义为：

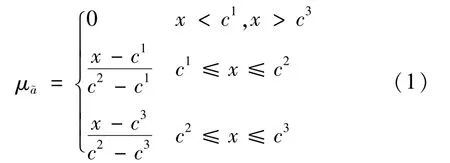
式中：c1、c2、c3满足c1≤c2≤c3；c1，c2，c3∈R且c1、c2分别表示上届和下届，并且它们能表示模糊度，c3-c1的值越大，模糊度越大。

定义2［14］算术运算

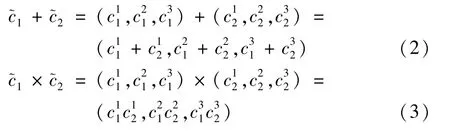
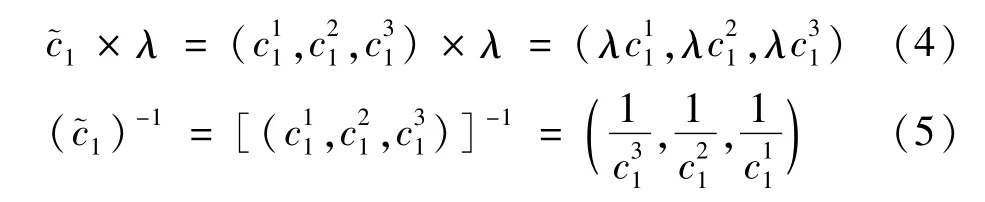
定义3［14］假设是比较n个元素相对优先级的判断，判断矩阵中的（i，j）元素代表元素i相对于j的相对重要性。满足以下条件：

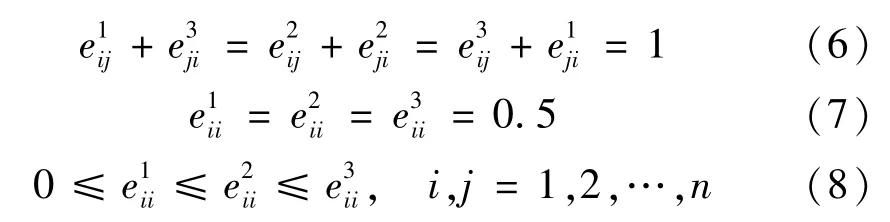
定义4［14］

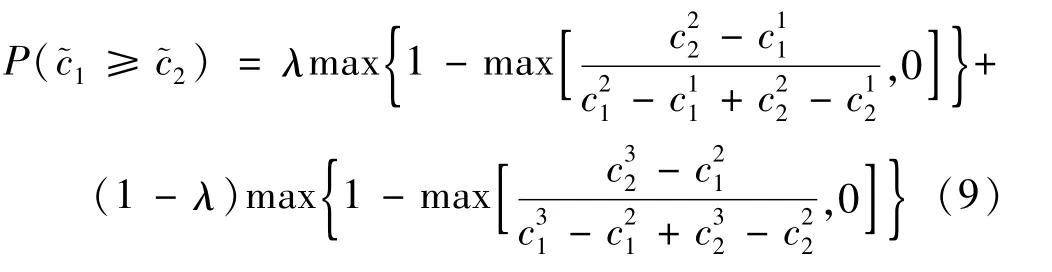
式中，λ是一个常数，代表决策者对风险的态度。当λ＞0.5时，意味着决策追求风险；当λ＜0.5时，意味着决策者不喜欢风险；而当λ=0.5，这意味着决策者对风险保持中立。相类似地有

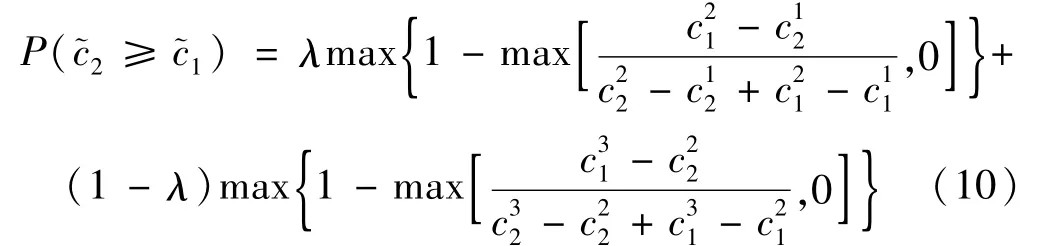
定义5［15］设~c=（c1，c2，c3）为模糊数，使用中心区域法进行模糊实数化，则最佳非模糊表现值（BNP）计算公式：

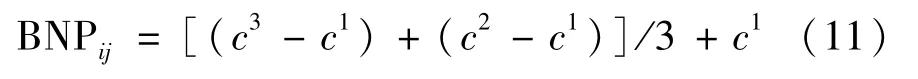
3 基于主客观赋权法的灰色关联综合评价模型

3.1 基于主客观赋权法的权重计算

3.1.1 基于模糊网络分析法确定指标的主观权重

模糊网络分析法是指由于客观环境等诸多因素的影响，决策者往往无法给出精确的偏好信息，因此将经典的ANP法中的构造判断矩阵的标度转换成三角模糊数，利用三角模糊数来表达决策者的偏好值。为此，将三角模糊数引入到ANP中，充分发挥三角模糊数在处理模糊性方面的优势，提升处理信息的准确性。

本文采用基于比较判断矩阵的模糊网络分析法来确定属性的权重。此方法的第一步是将问题修改为层次结构，即先利用模糊层次分析法来求出属性的独立权重，再利用模糊网络分析法求出全局权重。

假设该网络模型中，一级属性用K表示和2级指标用KL表示；则属性指标的全局权重计算步骤如下：

（1）采用模糊层次分析法［14］确定独立权重。

步骤1构造一级属性的聚合判断矩阵1根据三组不同决策者的意见及语言术语，可将决策者的意见根据表2转化为三角模糊数，并将三组意见整合为平均比较判断矩阵。

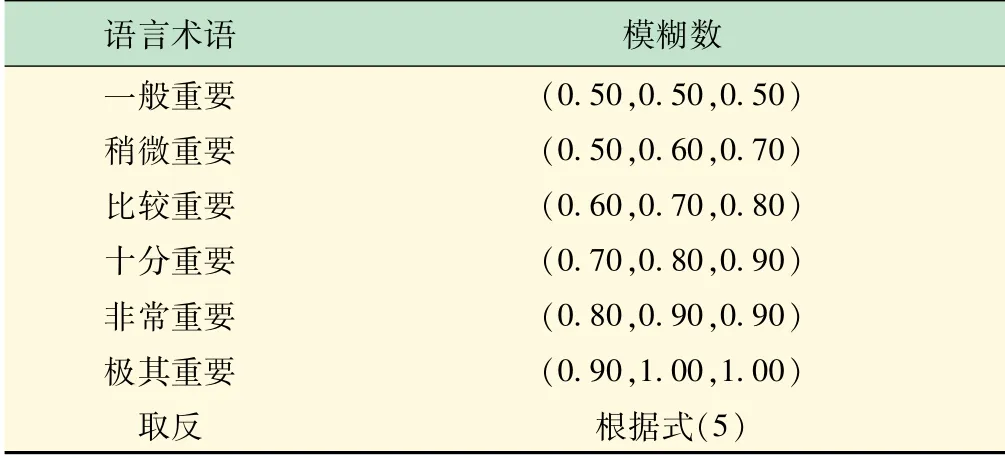
表2 语言变量及其对应模糊数

步骤2确定模糊权重

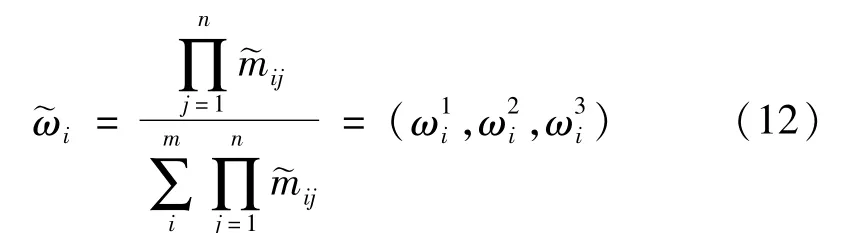
步骤3确定独立权重

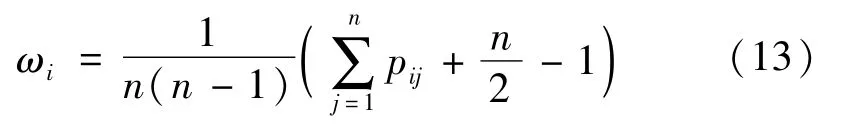
式中，pij为可能性矩阵，则

Pij（i=1，2，…，m；j=1，2，…，n）（表示i属性好于j的属性的可能度）。并且组成独立权重向量为W=｛W1，W2，…，WK｝。

步骤4根据决策者的2级指标的平均比较判断矩阵M～2，重复上述步骤2～3，计算得出2级属性指标的独立权重，组成权重向量~ωL=｛~ω1，~ω2，…，~ωKL｝。

（2）采用模糊网络分析法［16］确定全局权重。

步骤5根据决策者考虑指标相互作用的1级指标的平均判断矩阵，重复上述步骤2～3，计算得出内部交互矩阵IIM=｛iimL1L2｝K×K，其中iimL1L2（L1=1，2，…，K；L2=1，2，…，K）表示L1，L2之间的相互影响的权重。

步骤6确定相互依赖权重

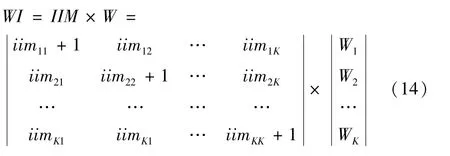
式中，WI=｛ωi1，ωi2，…，ωiK｝是相互依赖权重向量，ωiL（L=1，2，…，K）表示第L项指标下的相互依赖权重。

步骤7标准化相互依赖权重

步骤8确定主观权重

3.1.2 基于熵权法确定指标的客观权重

熵权法的基本思想是根据指标之间的差异来确定各项指标的权重，当某个指标的信息熵越小，表示该指标的变异程度越大，在评价过程中包含的信息越多，起到的作用越大，其相应的权重也就越大；反之越小：

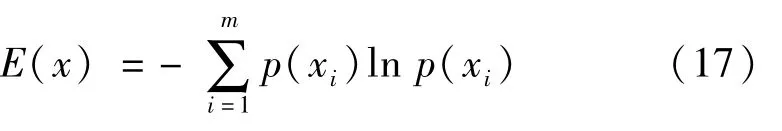
式（17）为信息熵的表达式。

熵值法［17］的计算步骤为：

步骤1根据式（11）将多个专家对属性值的偏好矩阵M～去模糊化得到M，对其各项指标根据公式进行标准化处理，数值越大越优型和数值越小越优型。即：

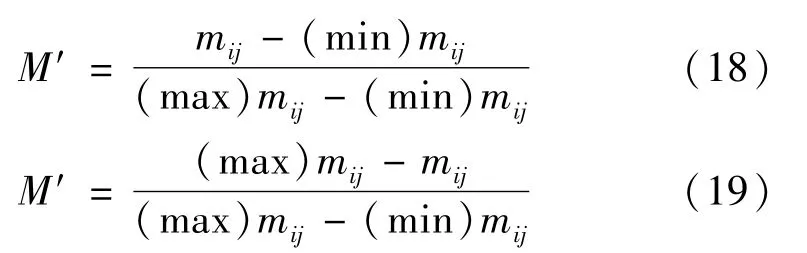
步骤2计算出第j项指标的信息熵

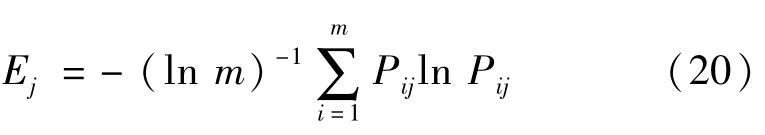
式中，i代表专家的个数，i=1，2，…，m。

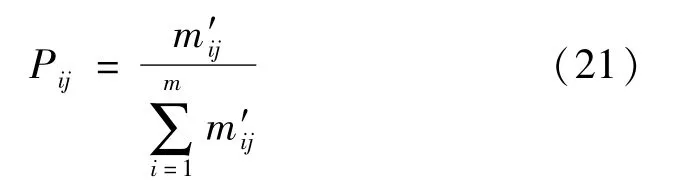
步骤3根据各个指标的信息熵计算出客观权重

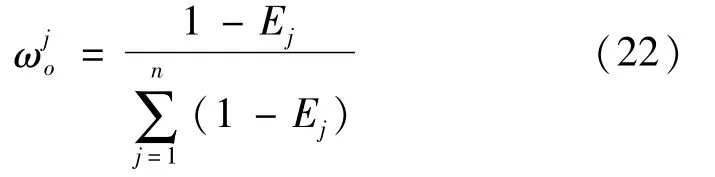
式中，j代表专家的个数，j=1，2，…，n。

3.1.3 确定指标的综合权重

在对高校实验室进行评价时，为了保证评价的客观性与合理性，本文采用了主观赋权和客观赋权法相结合的方法来确定指标的最终权重。

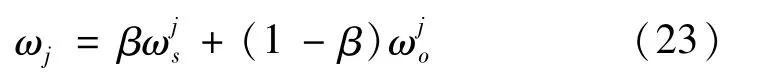
式中：ωj表示第j项指标的综合权重；β为权重协调系数；1-β代表主观权重所占比例。本文假设主观赋权和客观赋权所占的比例相同，即β=1-β=0.5，可以得到最终权重W=｛ω1，ω2，…，ωn｝。

3.2 灰色加权关联综合模型

假设有个m备选方案，每个备选方案包括n个评价指标。因此决策矩阵为j≤n）（其中为第i个备选方案第j项指标下的三角模糊数）；灰色关联分析法的步骤如下［14］：

步骤1对于定性指标，根据表3中7级因素等级对评价指标进行量化赋值为三角模糊数，得到决策矩阵X=（xij）m×n。

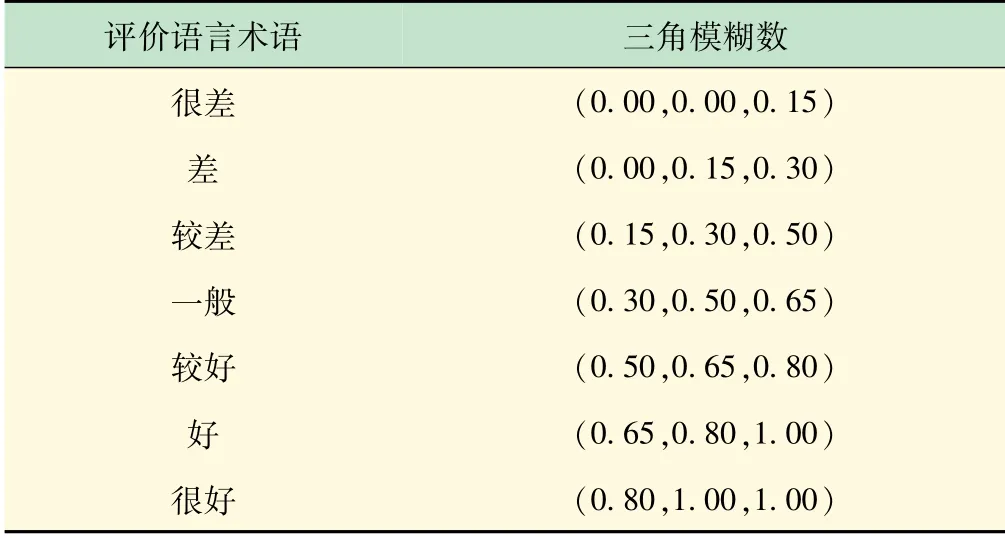
表3 语言变量及其对应模糊数

步骤2由于方案优选指标体系中各指标的计量单位和量纲不同，为弱化指标之间因量纲不同对综合评价结果造成的影响，需对指标进行规范化处理。根据式（24）和（25）进行规范化处理得到标准化决策矩阵Y=（~yij）m×n。经规范化后的指标值均变为越大越好型。

（1）效益性指标，即属性值越大越好的指标。

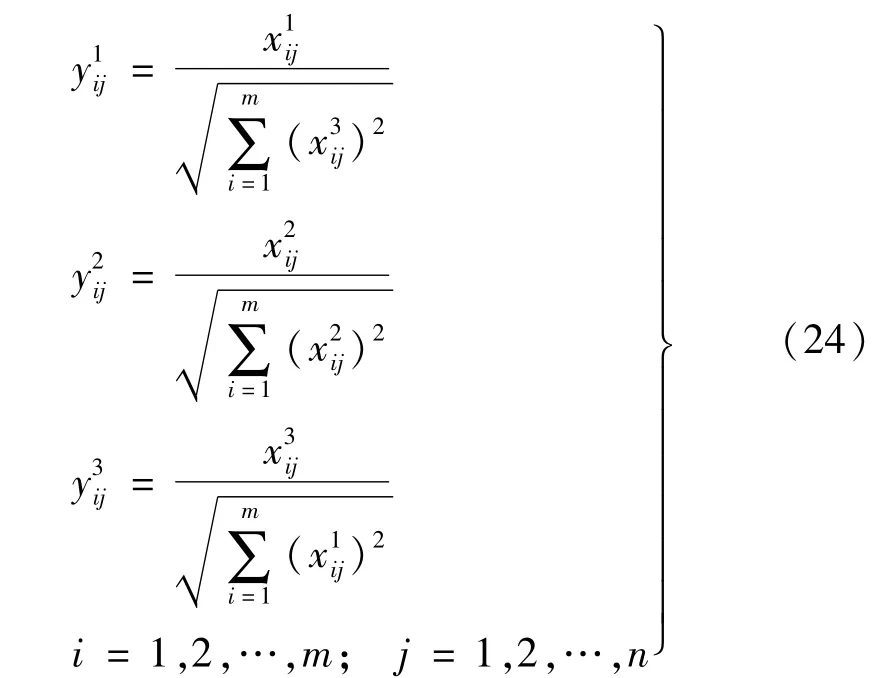
（2）成本型指标，即属性值越小越好的指标。

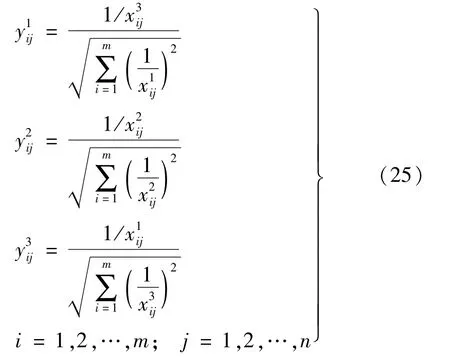
步骤3生成参考序列。由标准化后的决策矩阵构造关于所有指标的理想解决方案组成的参考序列n）表示j属性的最大值）

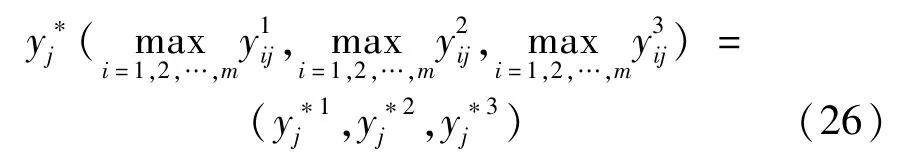
步骤4计算灰色关联系数

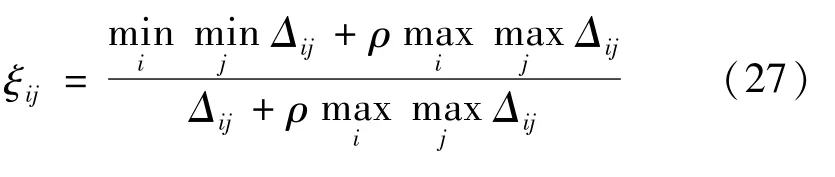
式中

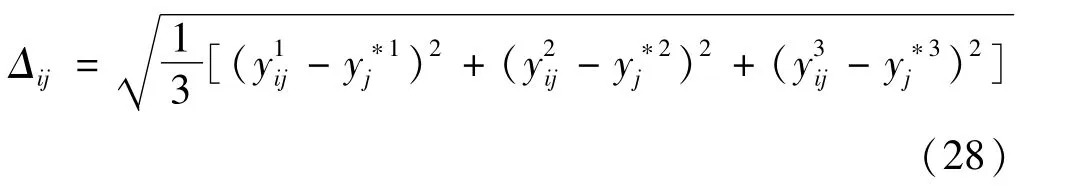
ρ为区分系数，ρ∈［0，1］，通常取ρ=0.5。

步骤5计算关联度。传统的关联度计算公式是求关联系数的算数平均值，并没有考虑各指标在整个评价体方案的综合优势度，该方法克服了传统灰色关联模型中均权的缺陷，提高了结果的精准度。系结构中所占的权重，即每个指标都是等权重值，而本文采用加权的方法，将指标的综合权重与关联系数相乘并求和作为最终每个备选

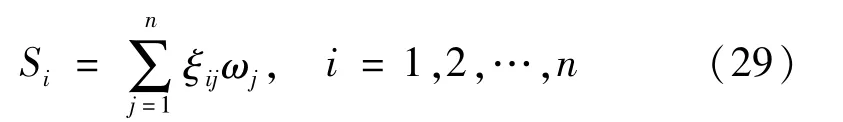
在确定每种备选方案的综合优势度，可以获得备选方案的优先顺序，而且Si的值越高，备选方案就越好。

4 实例分析

为了更好地提升实验室的建设水平，某航海类高校组织了实验室管理处、科技处、保卫处的3组专家对该校6个实验室（船机修造工程实验室A1、航海训练与工程实验室A2、航海动态仿真实验室A3、交通运输与物流教学实验室A4、轮机模拟实验室A5和救助与打捞实验室A6）进行评估。根据上文的评价指标体系进行评价打分。

步骤1确定聚合平均比较判断矩阵

根据专家的意见及语言术语，可将专家对1级指标，2级指标的比较意见偏好根据表2转化为三角模糊数，并将三组意见整合为平均比较判断矩阵如表4、表5、表6所示。

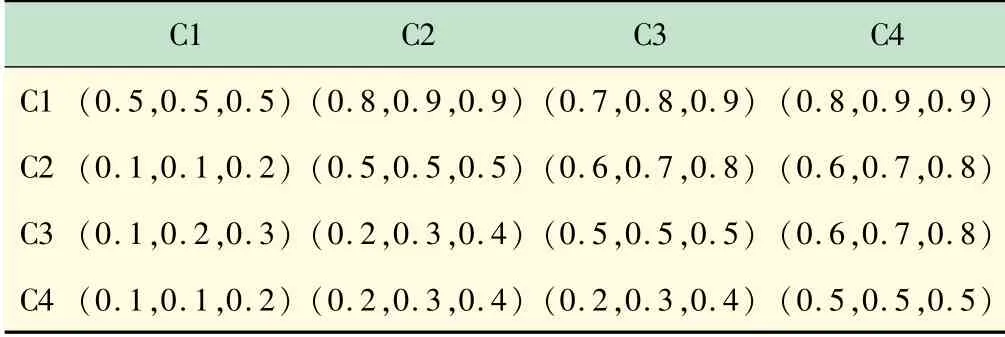
表4 具有模糊数的平均比较判断矩阵M～1

表5 具有模糊数的平均比较判断矩阵

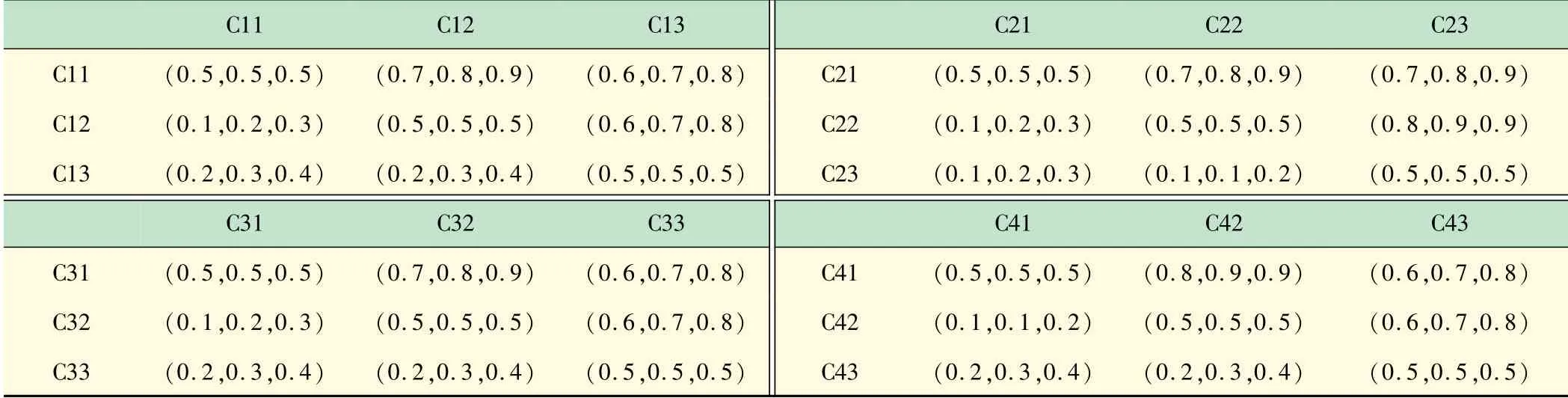
表5 具有模糊数的平均比较判断矩阵

C11 C12 C13 C21 C22 C23 C11（0.5，0.5，0.5）（0.7，0.8，0.9）（0.6，0.7，0.8）C21（0.5，0.5，0.5）（0.7，0.8，0.9）（0.7，0.8，0.9）C12（0.1，0.2，0.3）（0.5，0.5，0.5）（0.6，0.7，0.8）C22（0.1，0.2，0.3）（0.5，0.5，0.5）（0.8，0.9，0.9）C13（0.2，0.3，0.4）（0.2，0.3，0.4）（0.5，0.5，0.5）C23（0.1，0.2，0.3）（0.1，0.1，0.2）（0.5，0.5，0.5）C31 C32 C33 C41 C42 C43 C31（0.5，0.5，0.5）（0.7，0.8，0.9）（0.6，0.7，0.8）C41（0.5，0.5，0.5）（0.8，0.9，0.9）（0.6，0.7，0.8）C32（0.1，0.2，0.3）（0.5，0.5，0.5）（0.6，0.7，0.8）C42（0.1，0.1，0.2）（0.5，0.5，0.5）（0.6，0.7，0.8）C33（0.2，0.3，0.4）（0.2，0.3，0.4）（0.5，0.5，0.5）C43（0.2，0.3，0.4）（0.2，0.3，0.4）（0.5，0.5，0.5）

表6 具有模糊数的平均比较判断矩

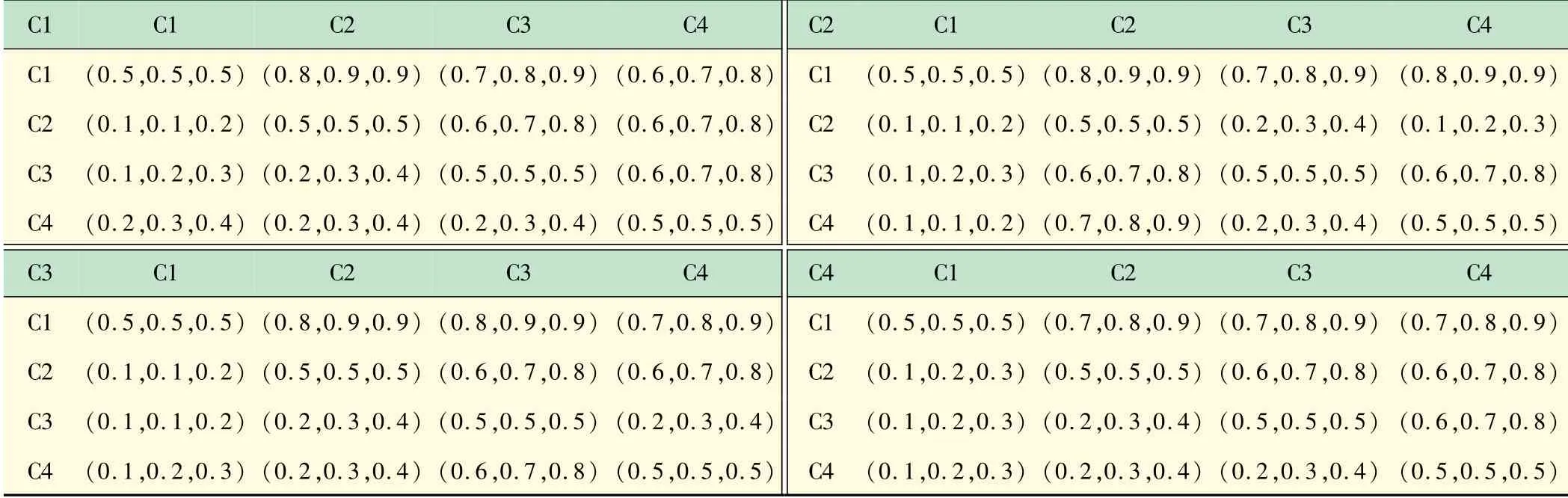
表6 具有模糊数的平均比较判断矩

C1 C1 C2 C3 C4 C2 C1 C2 C3 C4 C1（0.5，0.5，0.5）（0.8，0.9，0.9）（0.7，0.8，0.9）（0.6，0.7，0.8）C1（0.5，0.5，0.5）（0.8，0.9，0.9）（0.7，0.8，0.9）（0.8，0.9，0.9）C2（0.1，0.1，0.2）（0.5，0.5，0.5）（0.6，0.7，0.8）（0.6，0.7，0.8）C2（0.1，0.1，0.2）（0.5，0.5，0.5）（0.2，0.3，0.4）（0.1，0.2，0.3）C3（0.1，0.2，0.3）（0.2，0.3，0.4）（0.5，0.5，0.5）（0.6，0.7，0.8）C3（0.1，0.2，0.3）（0.6，0.7，0.8）（0.5，0.5，0.5）（0.6，0.7，0.8）C4（0.2，0.3，0.4）（0.2，0.3，0.4）（0.2，0.3，0.4）（0.5，0.5，0.5）C4（0.1，0.1，0.2）（0.7，0.8，0.9）（0.2，0.3，0.4）（0.5，0.5，0.5）C3 C1 C2 C3 C4 C4 C1 C2 C3 C4 C1（0.5，0.5，0.5）（0.8，0.9，0.9）（0.8，0.9，0.9）（0.7，0.8，0.9）C1（0.5，0.5，0.5）（0.7，0.8，0.9）（0.7，0.8，0.9）（0.7，0.8，0.9）C2（0.1，0.1，0.2）（0.5，0.5，0.5）（0.6，0.7，0.8）（0.6，0.7，0.8）C2（0.1，0.2，0.3）（0.5，0.5，0.5）（0.6，0.7，0.8）（0.6，0.7，0.8）C3（0.1，0.1，0.2）（0.2，0.3，0.4）（0.5，0.5，0.5）（0.2，0.3，0.4）C3（0.1，0.2，0.3）（0.2，0.3，0.4）（0.5，0.5，0.5）（0.6，0.7，0.8）C4（0.1，0.2，0.3）（0.2，0.3，0.4）（0.6，0.7，0.8）（0.5，0.5，0.5）C4（0.1，0.2，0.3）（0.2，0.3，0.4）（0.2，0.3，0.4）（0.5，0.5，0.5）

步骤2利用模糊ANP方法计算指标权重。

根据3.1.1节中式（12）～（16）计算并求得指标的主观权重如表7所示。

表7 指标主观权重

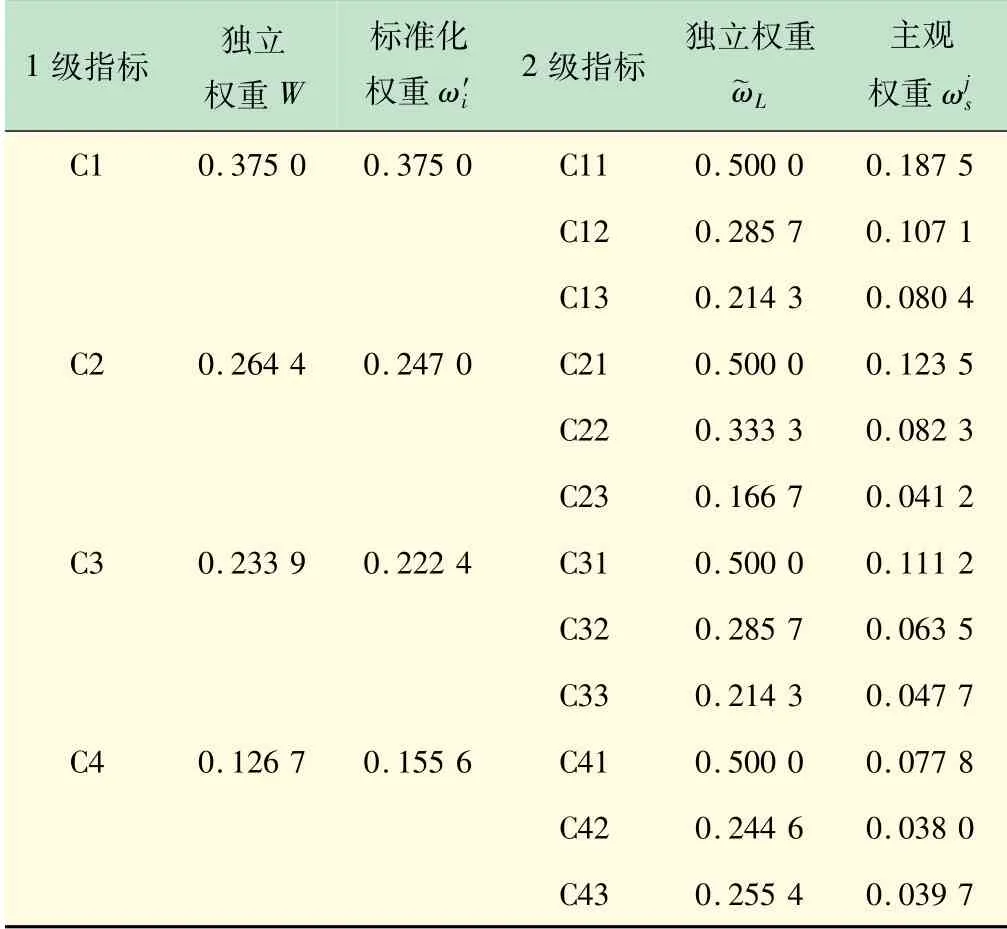
表7 指标主观权重

1级指标独立权重W标准化权重ω′i 2级指标独立权重~ωL主观权重ωj s C1 0.375 0 0.375 0 C11 0.500 0 0.187 5 C12 0.285 7 0.107 1 C13 0.214 3 0.080 4 C2 0.264 4 0.247 0 C21 0.500 0 0.123 5 C22 0.333 3 0.082 3 C23 0.166 7 0.041 2 C3 0.233 9 0.222 4 C31 0.500 0 0.111 2 C32 0.285 7 0.063 5 C33 0.214 3 0.047 7 C4 0.126 7 0.155 6 C41 0.500 0 0.077 8 C42 0.244 6 0.038 0 C43 0.255 4 0.039 7

步骤3利用熵值法计算指标的客观权重。

根据3名专家对各个指标进行评价，并根据表3将其语言术语转换为三角模糊数，如表8所示，根据3.1.2节中式（18）～（22）得到的指标的客观权重如下：

表8 3名专家对属性值的偏好矩阵

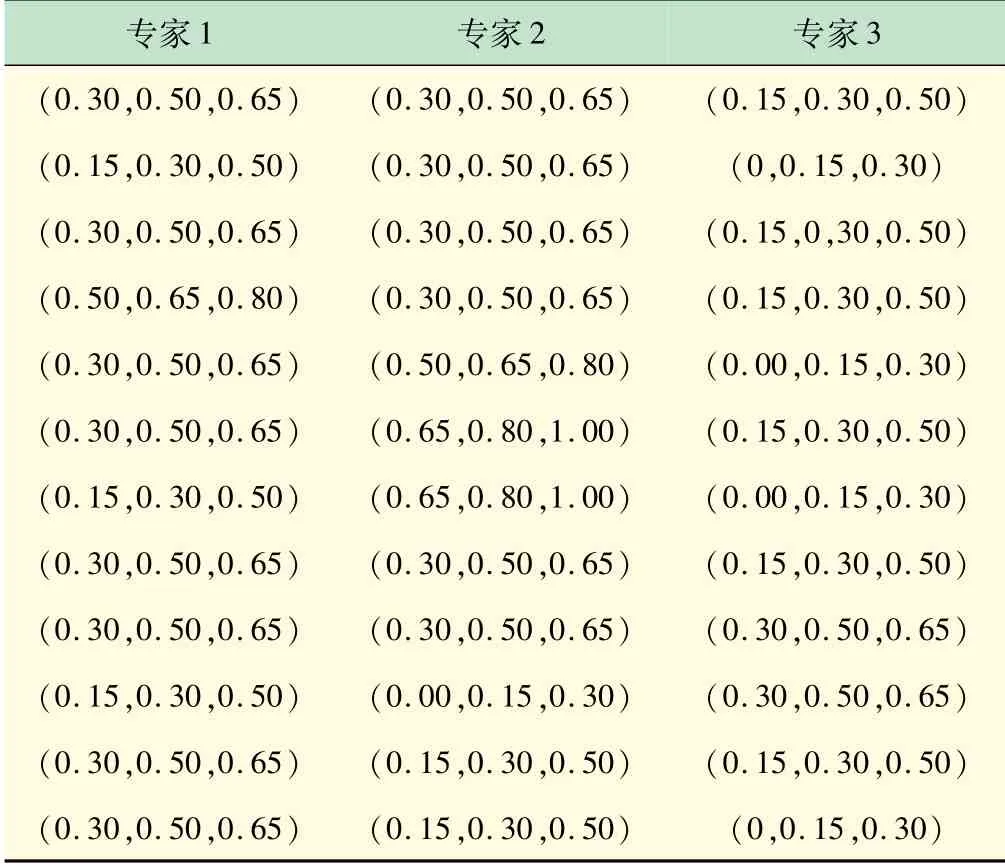
表8 3名专家对属性值的偏好矩阵

专家1专家2专家3（0.30，0.50，0.65）（0.30，0.50，0.65）（0.15，0.30，0.50）（0.15，0.30，0.50）（0.30，0.50，0.65）（0，0.15，0.30）（0.30，0.50，0.65）（0.30，0.50，0.65）（0.15，0，30，0.50）（0.50，0.65，0.80）（0.30，0.50，0.65）（0.15，0.30，0.50）（0.30，0.50，0.65）（0.50，0.65，0.80）（0.00，0.15，0.30）（0.30，0.50，0.65）（0.65，0.80，1.00）（0.15，0.30，0.50）（0.15，0.30，0.50）（0.65，0.80，1.00）（0.00，0.15，0.30）（0.30，0.50，0.65）（0.30，0.50，0.65）（0.15，0.30，0.50）（0.30，0.50，0.65）（0.30，0.50，0.65）（0.30，0.50，0.65）（0.15，0.30，0.50）（0.00，0.15，0.30）（0.30，0.50，0.65）（0.30，0.50，0.65）（0.15，0.30，0.50）（0.15，0.30，0.50）（0.30，0.50，0.65）（0.15，0.30，0.50）（0，0.15，0.30）

步骤4确定指标的综合权重

根据式（23）可得指标综合权重如下：

根据图1可以看出，主观赋权得到的指标权重数值较大，说明决策者的主观偏好和经验较强；而客观赋权法得到的指标权重数值较小，说明它仅依赖于数据本身的离散性，而没有考虑到决策者的经验等，客观性太强；综合来看，将主客观权重相结合得到的综合权重，反而更让指标的权重趋于适中，既考虑了决策者的经验及偏好，又考虑到了数据本身的特点，因此，在对实验室进行评估时，为了使决策结果的更加合理性和真实性，尽量选取综合赋权法来确定指标的权重。

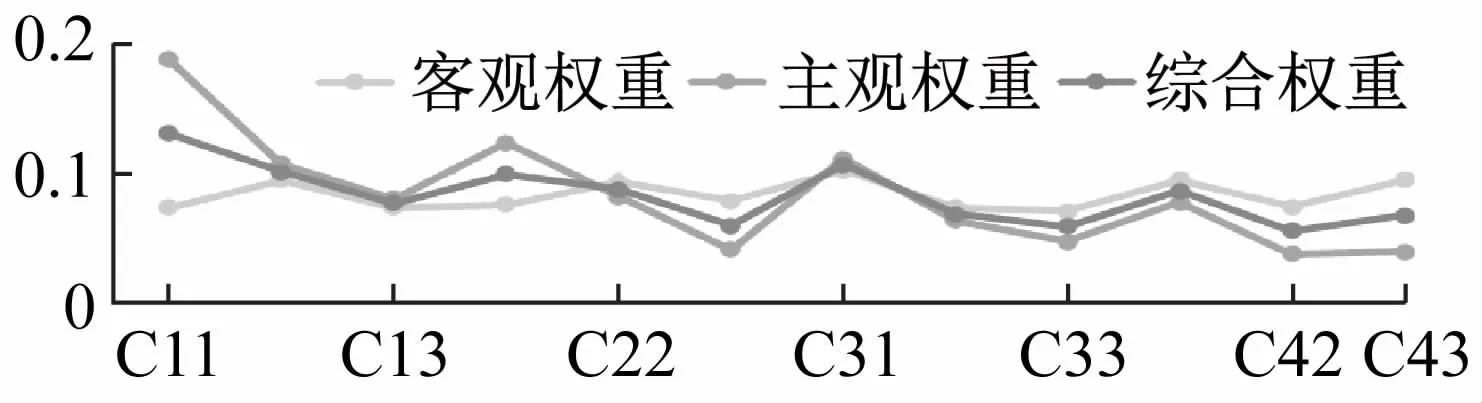
图1 主客观权重赋权法对比

步骤5确定三组专家的平均决策矩阵X=（xij）m×n。

三组专家需要根据表3对这6个实验室进行综合评分。由于每个决策者有不同的观点和意见，因此，可采用平均决策矩阵X=（xij）m×n用于对6个实验室进行评价，如表9所示。

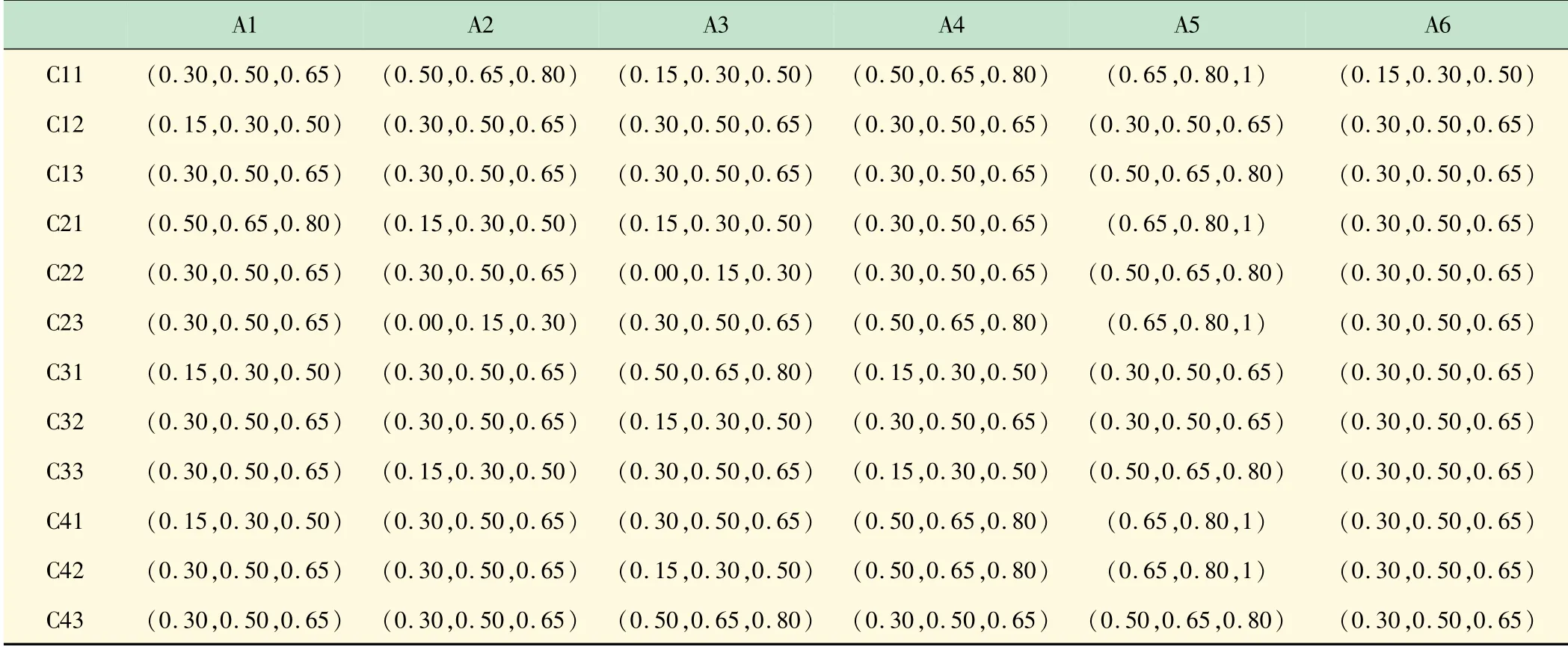
表9 平均决策矩阵

步骤6计算备选方案的综合优势度Si。

在确定实验室评价指标体系及权重的基础上，利用灰色关联分析对表9中的平均决策矩阵根据式（24）～（29）进行分析计算，得出6个实验室的评价结果如表10所示。

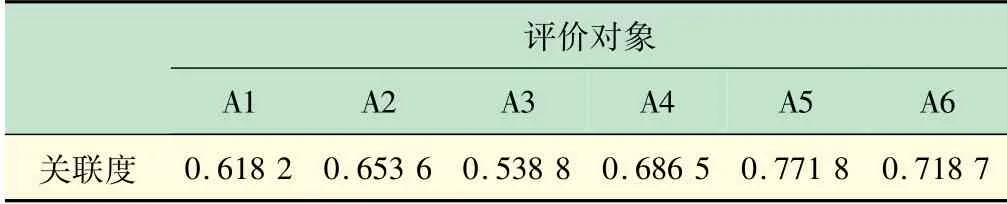
表10 实验室评价结果

由表9中的评价结果可知，6个实验室的评价排名为M5≻M6≻M4≻M2≻M1≻M3。可以发现，评价结果得分最高的是A5实验室，其次是A6，而A3实验室的得分最低。为了进一步探究各实验室得分水平的深层次的原因，继续结合各项指标分析实验室的得分水平，得出到表11中的结果。

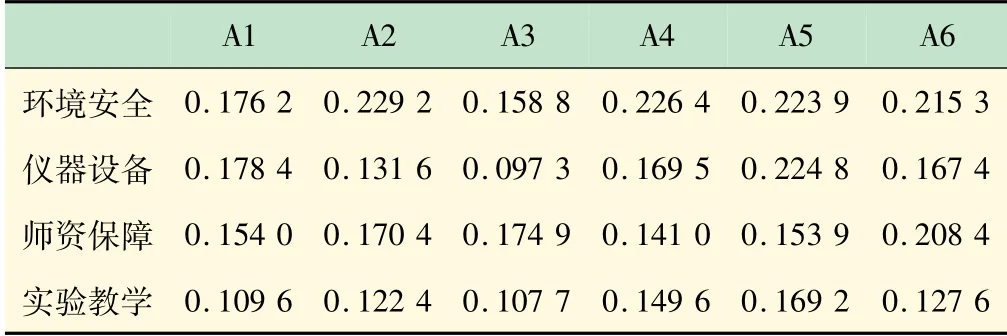
表11 各实验室在1级指标下的评价得分

从表11中可以看出，环境安全方面的权重设置相对较大，但是A1和A3实验室的得分较低，而其他实验室的得分情况差别不大，因此可以看出高等院校在实验室评估时，非常看重实验室的环境安全，这也就是A1和A3的综合排名较低的原因；在仪器设备方面，A5实验室评分更高一些，A3实验室最差，可能是由于A3实验室的仪器设备管理较差，资源共享不充分等，不能很好的完成实验项目；在师资保障方面，A6实验室评分较高一些，说明该实验室注重选取科研能力和实践能力很强的实验教师，为实验室项目的发展做好保障；在实验教学方面，A5和A4实验室都较为优秀，说明该实验室更加注重实验项目，而实验室如果不注重实验教学，进而会影响实验室排名的整体水平。这也是A5实验室与其他实验室相比，综合评价得分最高的原因。

5 结 语

本文针对航海类高校的特点，建立了高校实验室评价指标体系，并基于三角模糊数的概念，充分和网络分析法相结合来求解属性的主观权重，为了解决各指标层内各元素的相互作用以及指标评价的模糊性所造成权重严重偏差问题，即构建基于比较判断矩阵的模糊网络分析法；采用熵权法确定指标的客观权重，并将主客观权重相结合的组合赋权法对各类指标的权重进行求解，最后通过灰色关联分析法对某航海类高校6个实验室进行评价。本文将决策者的权重视为相同，将求得平均决策矩阵来进行计算，日后还可以考虑到决策者在评价时的重要性程度不同，因而权重不同，可进行改进。此外排序方法还可以与TOPSIS、VIKOR等其他方法相结合，对备选方案进行排名。