双层定型相变墙体的优化组合

党 昕，孟 多，高 慧

(辽宁工业大学土木建筑工程学院，锦州 121001)

据国际能源机构的数据统计，预计到2050年，建筑供暖与制冷的能耗将分别达到世界能源总消耗量的12%与37%[1]，降低建筑能耗已是当前世界上大多数国家亟待解决的能源问题之一。建筑围护结构在调节室内外环境之间的冷热负荷中起着举足轻重的作用，通过改善围护结构的保温隔热性能可达到显著的建筑节能效果，是降低建筑能耗的有效方式之一。

新型高效的保温建筑材料是有效提升建筑围护结构保温隔热性能的关键技术，其中相变材料(phase change material，PCM)由于能够依靠自身的固-液相转变实现潜热的吸收和释放，从而改变室外热量向室内传递的数量及时长，因此已经被广泛研究及应用于围护结构中发挥建筑调温、蓄热等建筑节能效能，且在近期的研究与应用中取得了可观的成效。Müslüm等[2]对含相变材料的建筑外墙的热工性能进行了数值研究，以土耳其的三个城市(迪亚巴克尔、科尼亚和埃尔祖鲁姆)为研究对象进行计算，验证了相变材料的使用位置、熔化温度和相变层厚度对节能、减量系数和时滞的影响；Kishore等[3]在对含相变材料的墙体进行数值研究时，确定了位于不同国际节能准则气候区的5个美国城市中的最佳相转变温度、墙体中的最佳相变材料位置以及集成相变材料的建筑墙体的节能潜力；Yun等[4]在研究中将每个相变材料应用于建筑体积的0.1%～0.9%，结果表明节能量最高为每年3.19 kWh/m2；金国辉等[5]基于ANSYS软件计算分析了内蒙古草原民居相变墙体的传热特性，结果表明相变材料层厚度、对流换热系数和相变潜热对内壁面温度响应具有显著的节能性影响；张维维等[6]则采取实验研究的方法，以填有相变材料的空心砌块所砌成的相变南外墙为研究对象，利用控温热箱装置研究其传热性能，验证了相变墙体的热惰性强于普通墙体，且外界温度波幅越大、外界平均温度与相变材料平均温度越接近，相变墙体对温度和热流的衰减和延迟效果越明显。

随着研究的深入，研究者发现受相变材料的应用形式限制，相变蓄热围护结构的蓄热密度较纯相变材料有大幅降低，因此单层相变材料的节能效果不能满足节能标准，进而提出了双层组合式相变蓄热围护结构，以期增强相变围护结构的节能效果，拓展相变蓄热温度范围。张源等[7]提出将两种不同相变温度的相变材料同时填入到多层平壁墙体中，低相变温度的PCM在冬季的利用率和高相变温度 PCM 在夏季的利用率均为 0～100%；罗振宇等[8]将制备的相变材料板以“三明治”形式贴于轻质实验房南墙内外侧，结果表明夏季外侧相变墙发挥作用，能够很好地吸收太阳辐射的热量，降低并延缓室内温度峰值。综上所述，研究双层定型相变墙体对典型气候地区的室内温度调控十分有必要。近年来，本课题组对建筑节能用定形相变材料的开发、性能及建筑节能应用效果进行了系统研究。为进一步深入研究和验证该类定形相变材料在不同气候分区的建筑节能应用形式和效果，推动其建筑节能应用发展，现拟构建不同相变温度和厚度组合的双层定型相变墙体，采用显热容法建立双层定型相变墙体的传热过程模型，并利用有限元软件求解得到外墙内表面温度变化曲线，分析其控温规律及节能潜力，探究双层定型相变墙体在不同热功能分区的最佳相变温度、厚度组合结构形式，以期为相变节能建筑的推广应用提供理论支持，为使用双层定型相变墙体的建筑节能设计提供数据参考。

1 双层定型相变墙体的物理模型

实际建筑墙体结构的长、宽尺寸较大，为简化计算，将双层定型相变墙体的传热过程是视作内外表面之间的一维传热，即如图1所示的沿厚度x方向的一维传热过程。双层定型相变墙体的结构主要包括4个部分，最外侧为200 mm厚的钢筋混凝土结构层，中间两层分别为两种不同相变温度和潜热的定形相变材料保温层，最内层为水泥砂浆面层，厚度为20 mm。相变保温层材料分别采用白乳胶和膨胀珍珠岩(EP)封装后的32#、25#石蜡(PCM-A，PCM-B)、相变石蜡/聚甲基丙烯酸甲酯(PMMA)相变蓄热板(PCM-C)以及癸酸-月桂酸(CA-LA)/硅藻土定形相变材料(PCM-D)。以上材料均为本课题组近两年新制的定形相变材料，其热物性、热稳定性、形状保持能力及力学性能等均已得到优化，可应用于建筑围护结构。双层定型相变墙体的保温层由两种不同定形相变材料组成，构成具有不同相变温度和相变潜热组合式双层相变蓄热保温结构。目前已有研究表明相变蓄热层的厚度为30～50 mm可使传热与节能效果较好[11]，因此为考查确定相变保温层的厚度，4种定形相变材料蓄热层的厚度均选取30、40、50 mm 3种规格，两两组合共构建54种双层定型相变墙体。双层定型相变墙体的各层材料热物性参数如表1所示。

图1 双层定型相变墙体热传导物理模型Fig.1 Physical model diagram of heat conduction of double-layer shaped phase change wall

表1 双层定型相变墙体组成材料热物性参数Table 1 Thermophysical parameters of the double-layer shaped phase change wall components

2 双层定型相变墙体的数学模型

2.1 数学方程及假设

相变墙体传热过程计算采用显热容法。显热容法将相变材料的相变潜热视为在一个很小温度范围内的大显热容，从而将分区描述的相变问题转化成单一区域上的非线性导热问题，进而对整体进行求解。在求解时，显热容法以温度为唯一待求参数在整个区域中建立能量方程，因此求解更容易，计算更直接[9]。基于显热容法的传热方程为

(1)

ρ=θ1ρ1+θ2ρ2

(2)

(3)

(4)

K=θ1K1+θ2K2

(5)

θ1+θ2=1

(6)

式中：ρ为相变材料的密度；ρ1为相变材料固态时密度；ρ2为相变材料液态时密度；c为材料的比热容；c1为相变材料固态时比热容；c2为相变材料液态时比热容；θ为质量分数；θ1为固态相变材料占整个相变材料的质量分数；θ2为液态相变材料占整个相变材料的质量分数；αm为质量分数，取值在-0.5～0.5；l1→2为由固态转向热态相变材料的熔化潜热；T为温度；t为时间；K为导热系数；K1为相变材料固态时的导热系数；K2为相变材料液态时的导热系数；∇为温度在空间中的变化梯度。

在进行以上计算时，对整个双层相变墙板做出以下假设：①忽略在发生相变时，相变材料固、液相之间的热对流；②在相变过程中，显热容法即将材料的相变潜热并到热容中，因此除材料的比热容之外，其密度与导热系数都为相变材料固态时所对应参数；③对各个墙板之间的材料层之间忽略其接触热阻；④相变过程发生在一个温度区间，且在此区间内相变潜热以热容的形式存在；⑤墙体内部的各层材料均为各向同向性。

2.2 边界条件

当t=0时：x上所对应的各个厚度方向上的温度为初始温度，其中x=0处为室外温度t1；x=L1+L2+L3+L4处为室内温度t2。

2.3 室内计算温度

根据《民用建筑供暖通风与空气调节规范》(GB 50736—2012)[10]，民用建筑舒适性空调的室内计算温度取值分别为：夏季25 ℃，冬季18 ℃。

2.4 室外计算温度

对任一时刻，建筑围护结构夏季空调室外计算温度为

TW,τ=TW,a+βτΔTW

(7)

式(7)中：TW，τ为室外计算逐时温度，℃；TW,a为室外计算日平均温度，℃；βτ为室外空气温度逐时变化系数；ΔTW为室外计算平均日较差，计算公式为ΔTW=(TW,τ-TW,a)/0.52，℃；TW为夏季室外计算干球温度，℃。其中TW、TW,a可由所在城市室外气象参数查得。

室外空气综合温度，即所采取的室外计算温度计算公式[12]为

(8)

式(8)中：P为围护结构材料吸收太阳辐射的吸收系数，取0.69；J为太阳吸收强度，W/m2，根据地区逐日逐时的气象资料获得；σ为空气对流换热系数，W/(m2·K)，夏季取15 W/(m2·K)，冬季取25 W/(m2·K)；ε为墙体外表面长波辐射系数；ΔR为有效辐射，W/m2，由于ΔR的确定较复杂，取近似值ΔR=3.5σ/ε,根据计算与整合取εΔR/σ=3.6。

选取中国夏热冬冷和严寒地区两个典型气候区进行研究，其中，夏热冬冷地区的代表城市为成都，严寒地区为西宁，经计算得出这两个城市冬、夏两季典型日的室外计算温度曲线(图2)。根据所建立的双层相变墙体传热过程模型，应用COMSOL Multiphysics有限元软件，计算出各不同组合形式的双层定型相变外墙的内表面48 h逐时温度变化曲线。

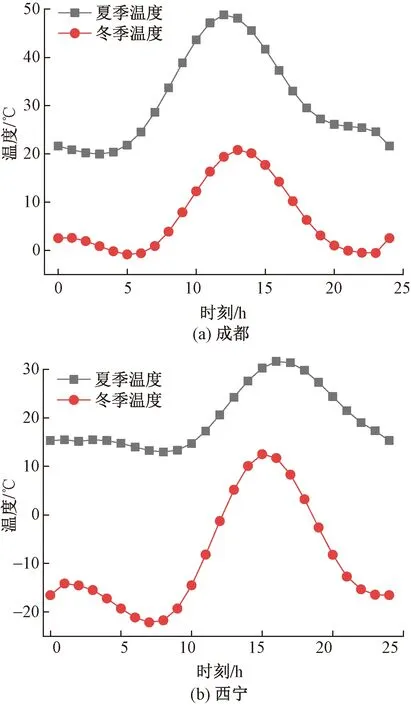
图2 成都与西宁冬、夏典型日室外计算温度曲线图Fig.2 Outdoor calculated temperature curve of winter and summer typical days in Chengdu and Xining

3 模拟结果及讨论

根据对54种不同相变温度与厚度组合的双层定型相变墙体的传热过程的模拟结果，筛选出具有外墙内表面温度波动小、接近人体舒适温度的墙体结构温度变化曲线及相反效果的墙体结构温度变化曲线，所涉及的双层定型相变墙体编号和墙体结构如表2所示。依据温度变化曲线讨论双层定型相变墙体对室外温度的响应过程及控温效能，分析相变墙体所在热工分区及不同季节的优化组合形式。

表2 双层定型相变墙体结构Table 2 Structure of the double-layer shaped phase change walls

3.1 夏热冬冷地区夏季传热模拟结果

为对比双层及单层定型相变墙体的隔热效果，取100 mm厚的PCM-A单层定型相变墙体为参照，同时进行传热过程模拟，经对比分析，成都市夏季代表性墙体结构形式的外墙内表面温度变化曲线如图3所示。由图3可见，墙体结构5的隔热效果最为显著，PCM-A单层相变墙体结构的隔热效果次之，墙体49的隔热效果最差。结构5的双层相变保温层和PCM-A单层相变保温层的厚度均为100 mm，结构49的双层相变保温层厚度为60 mm，尽管结构49的平均蓄热密度较前两者大，但相变潜热总容量却减小很多，可见相变蓄热层的厚度对建筑墙体隔热效果的影响较大。同时，双层相变墙体的隔热效果比同等厚度相变层的单层相变墙体的隔热效果好，在墙体结构5中，PCM-B和PCM-C的相变潜热之和小于单层的PCM-A，且PCM-A的相变温度更高，但实际的温控效果则弱于双层相变墙体，可见两种不同热物性的相变材料经过协同作用，能够有效削弱室外热量向室内传递的能力，并延缓室内高温出现时间，隔热效果显著。经相变材料的相变蓄热厚，建筑室内相对高温的时段延后至夜晚，可有效改善白天空调用电量过于集中的问题，节省空调制冷能源消耗。另外，研究得出相变材料的选择受室外温度影响较大，外侧的相变材料层应选取略低于室外高温的相变材料，内侧的相变材料层应选取略低于室内温度的相变材料，两者之间需要控制一定的温度梯度，温度梯度则由外层相变材料对室外高温的削弱程度来决定，导热系数越小，其热削弱效果越好，温度梯度也较大；相变潜热越大，温度梯度也相应较大。

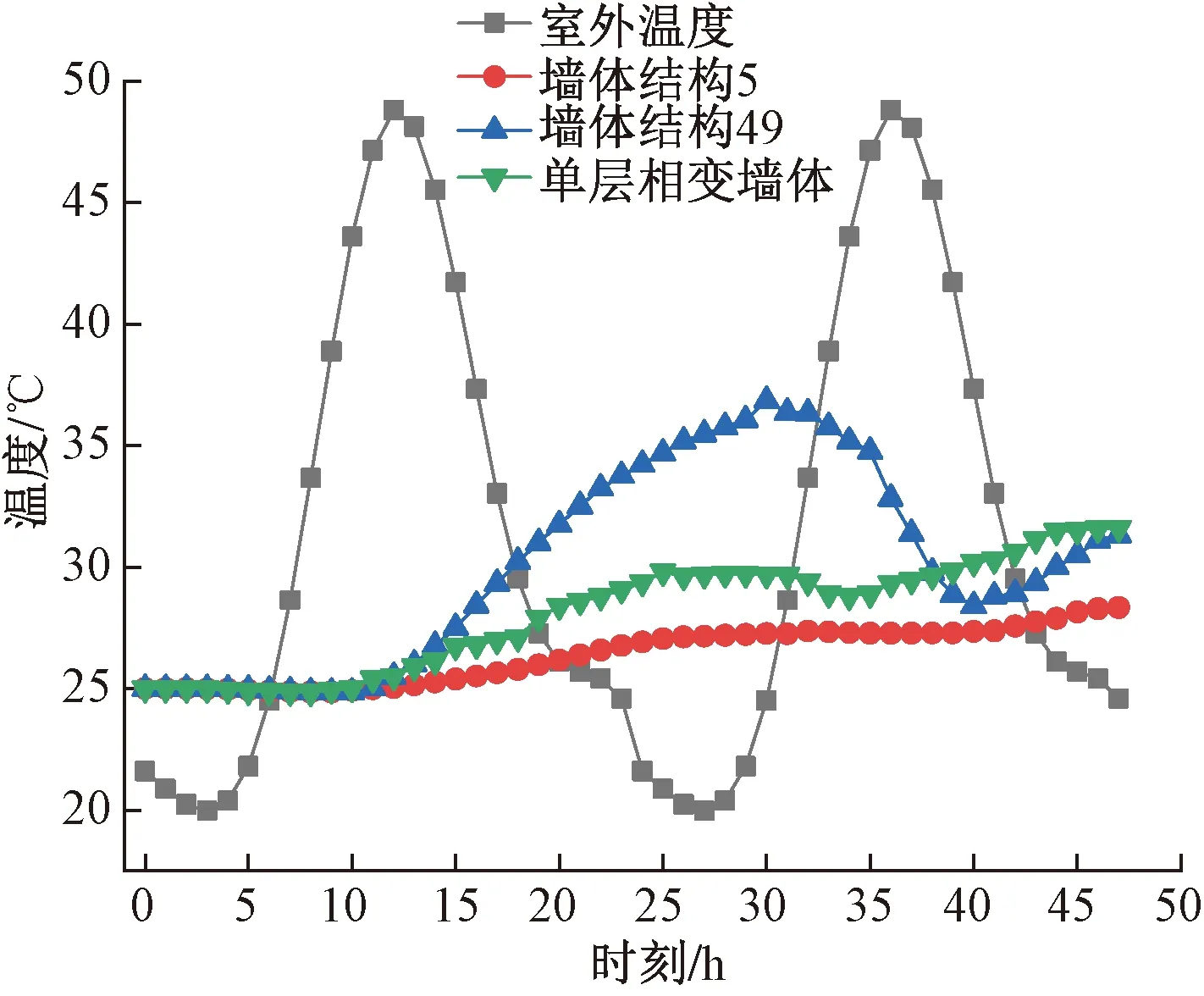
图3 成都夏季双层定型相变墙体模拟结果Fig.3 Simulation results of the double-layer shaped phase change walls in Chengdu in summer

3.2 夏热冬冷地区冬季传热模拟结果

在研究成都地区冬季的保温效果时，对照组选取相变层为100 mm厚的PCM-D(单层相变墙体1)与为100 mm厚的PCM-A(单层相变墙体2)，计算得到的典型墙体内表面温度变化曲线如图4所示。由图4可知，冬季时墙体结构6的保温效果最佳，墙体结构49的保温效果最差，单层相变墙体1和2介于二者之间，且1好于2。该结果再次证明，相变蓄热层的厚度对建筑墙体的保温隔热效果影响显著，100 mm厚单层相变墙体1的保温效果比60 mm厚双层相变墙体49的保温效果更好。墙体结构6采用的相变保温层为50 mm PCM-C+50 mm PCM-D，两种定形相变材料的相变温度分别为22 ℃和17.68 ℃，在中午高温时段能够实现吸收一定的相变潜热，在低温时段通过凝固过程释放潜热以维持外墙表面较高的温度。而双层定型相变墙体结构49中定形相变材料的相变温度都高于冬季室外温度，无法实现相变过程，加之厚度小，保温效果不尽理想。单层相变墙体2的PCM-D墙体的初始保温效果较好，这是由于PCM-D的相变温度与环境温度非常接近，中午室外温度超过18 ℃时，太阳辐射热经过钢筋混凝土层的削弱之后传入相变材料层，发生相变蓄热并在低温时释放热量，维持墙体较窄的温变范围。但是随着相变蓄放热过程的终止，室内温度则发生较大的波动。同样的，以100 mm厚PCM-A作相变层的单层相变墙体2的温度变化曲线可见，因室内与室外热量进行传递时皆达不到熔点31.5 ℃，使相变材料的相变潜热无法得到应用，因此不仅延缓高温出现的时间较短，对室外温度变化也较敏感，导致室内温度波动较大。由此可见，虽然双层相变材料可以起到二次保温的效果，但因环境温度低于材料的相变温度且波动较大，受相变反应时间的限制导致相变层的相变过程没有发生或发生不完全，相变材料的潜热蓄热能力不能充分发挥，因此由相变层厚度造成的显热热容的变化对冬季保温效果将起到决定性作用，且相变蓄热材料的温度应满足低温相变的条件，能够保证在冬季发挥相变蓄放热功能。

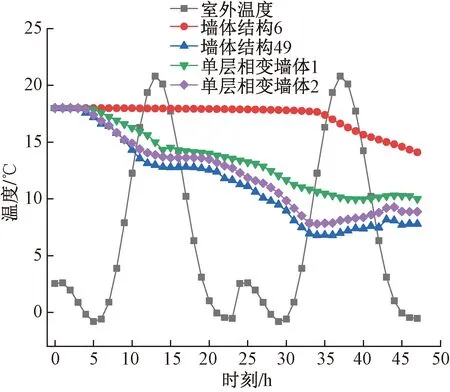
图4 成都冬季双层定型相变墙体模拟结果Fig.4 Simulation results of the double-layer shaped phase change walls in Chengdu in winter

3.3 寒冷地区夏季传热模拟结果

经计算，西宁夏季14：00—15：00的太阳辐射量较大，最高温度虽达31 ℃，日落后室外温度会迅速降至人体舒适温度附近，即高温状态并不持久，因此对相变墙体隔热效能要求并不严格。以100 mm厚的PCM-C作为单层相变墙体对照组，筛选出的典型墙体结构温度变化曲线如图5所示。由图5可见，墙体结构41可最大限度保持室内温度在夏季人体舒适温度范围内，温度范围为22.4～25 ℃，温度变幅2.6 ℃；墙体结构10的隔热效果也较好，温度变化介于20.5～25 ℃，但温度变幅较大，为4.5 ℃；墙体结构35和单层相变墙体的隔热效果较差，特别是结构35，温度范围及波动幅度均较大，对舒适度和节能不利。经分析可知，由于西宁夏季温度整体较低且高温与低温持续时间较短，PCM-A的相变作用得不到发挥，因此不在节能考虑范围内。单层PCM-C的相变温度为22 ℃，能保持较长时间的相变蓄热功能，作为单层保温墙体表现出了一定的隔热能力，温度波动小，但绝大部分时间温度高于25 ℃，节能潜力不大。双层定型相变墙体41和10的外层相变材料均为PCM-B，其相变温度低于白天室外温度，可以发生相变吸热反应，且其相变潜热值较大，所以使用PCM-B作为外层相变保温层的墙体结构均表现出了类似的隔热控温能力。结构10的控制温度较低是因为其PCM-B的厚度为50 mm，且内侧墙体采用的40 mm厚的PCM-C，相比结构41的30 mm PCM-B+50 mm PCM-D的双层相变结构，厚度和平均潜热值都较大。结构41中两种相变材料的相变温度相差较大，低温相变材料的厚度较大，能够在较高和较低的温度范围分别启动相变蓄/放热功能，营造白天温度低、夜晚温度高的控温效果，温度波动较小，而且控温范围也符合夏季舒适温度区间。同时相变层厚度的降低有利于减轻结构自重和建筑成本，因此更加适宜西宁地区。经数据分析，所构建的54种墙体结构中，很多类似结构41的双层定型相变墙体都表现出相似的温度变化趋势，鉴于此，结合夏季西宁室外温度变化特点，可以认为相变层厚度不是该地区夏季双层定型相变墙体选型的决定性因素，不同相变温度的组合对控制温度及温度波动具有更积极的作用。

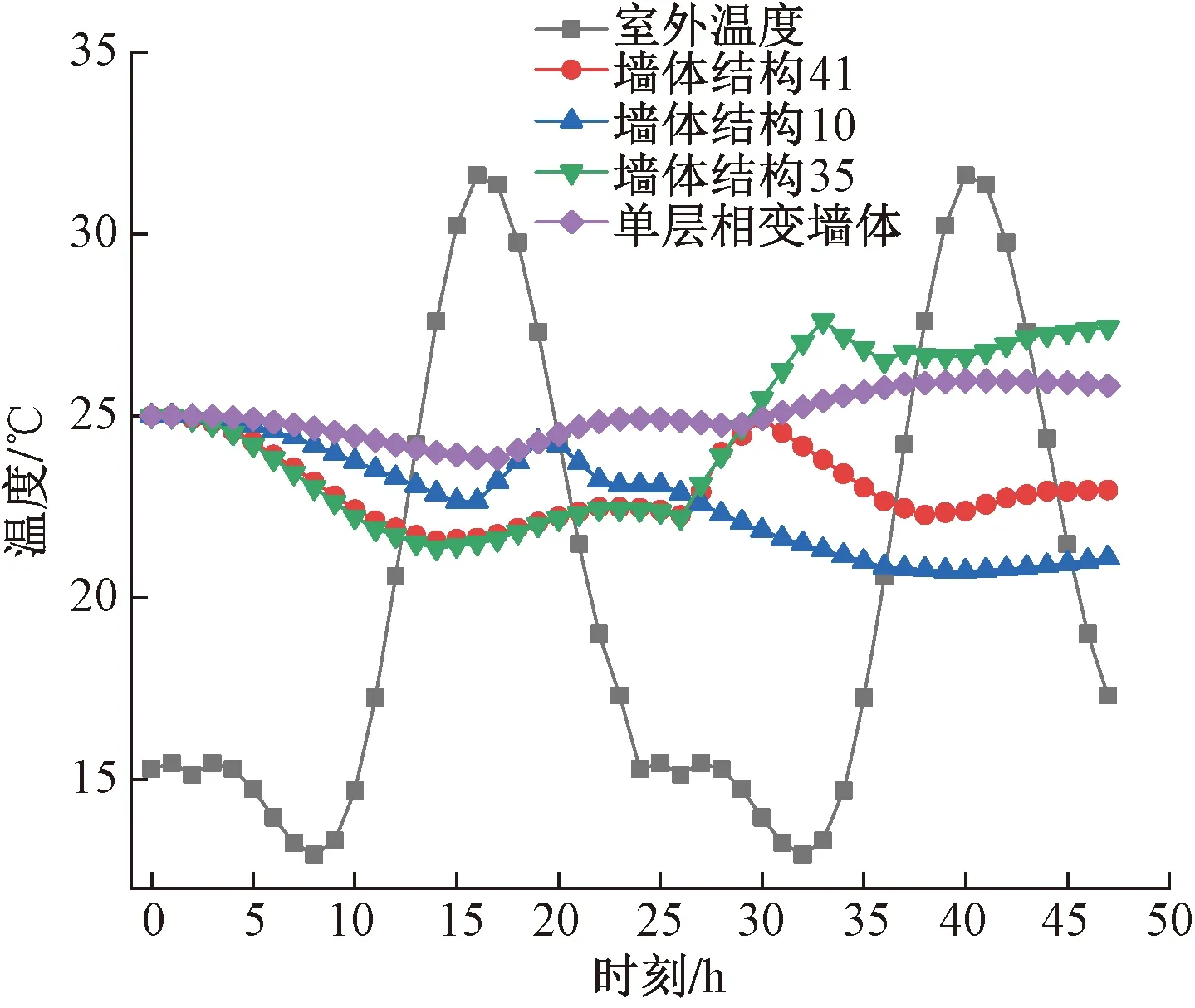
图5 西宁夏季双层定型相变墙体模拟结果Fig.5 Simulation results of the double-layer shaped phase change walls in Xining in summer

3.4 寒冷地区冬季传热模拟结果

西宁冬季的平均气温为-8 ℃，供暖期为10月中旬到次年4月中旬，冬季的供暖能耗较夏季空调能耗大得多，对于墙体保温性能要求较高，因此相变蓄热墙体应发挥显著的冬季隔冷、保温效果。在研究时，以100 mm厚PCM-C的单层相变墙体为对比样，经计算、分析得到西宁冬季典型墙体结构的内表面温度变化曲线如图6所示。由图6可见，墙体结构6的保温效果相对较好，结构49的保温效果较差，PCM-C单层相变墙体介于二者之间。该结果与夏热冬冷地区冬季的模拟结果相似，可见相变保温层的厚度对围护结构保温效果影响最大。组合相变温度的双层相变墙体6较单层效果显著，是因为内侧的PCM-D相变层能够在接近室温的17 ℃左右发生相变释热，对保持温度起到了一定的作用，但恒温阶段持续时间不长，之后温度迅速降低。而结构49中使用的PCM-A和PCM-B由于相变温度高出环境温度太多，没有发生相变过程且厚度薄，不能发挥保温效能。由计算可见，冬季时相变材料保温层的相变温度应靠近环境温度，其中外侧保温层的相变温度应略低于内侧保温层，如果室内有采暖设备，内侧墙体可蓄存高温时段的热量在低温时段释放，有利于节能。同时，为提高热容，相变层厚度在考虑经济性的同时应适当增大。

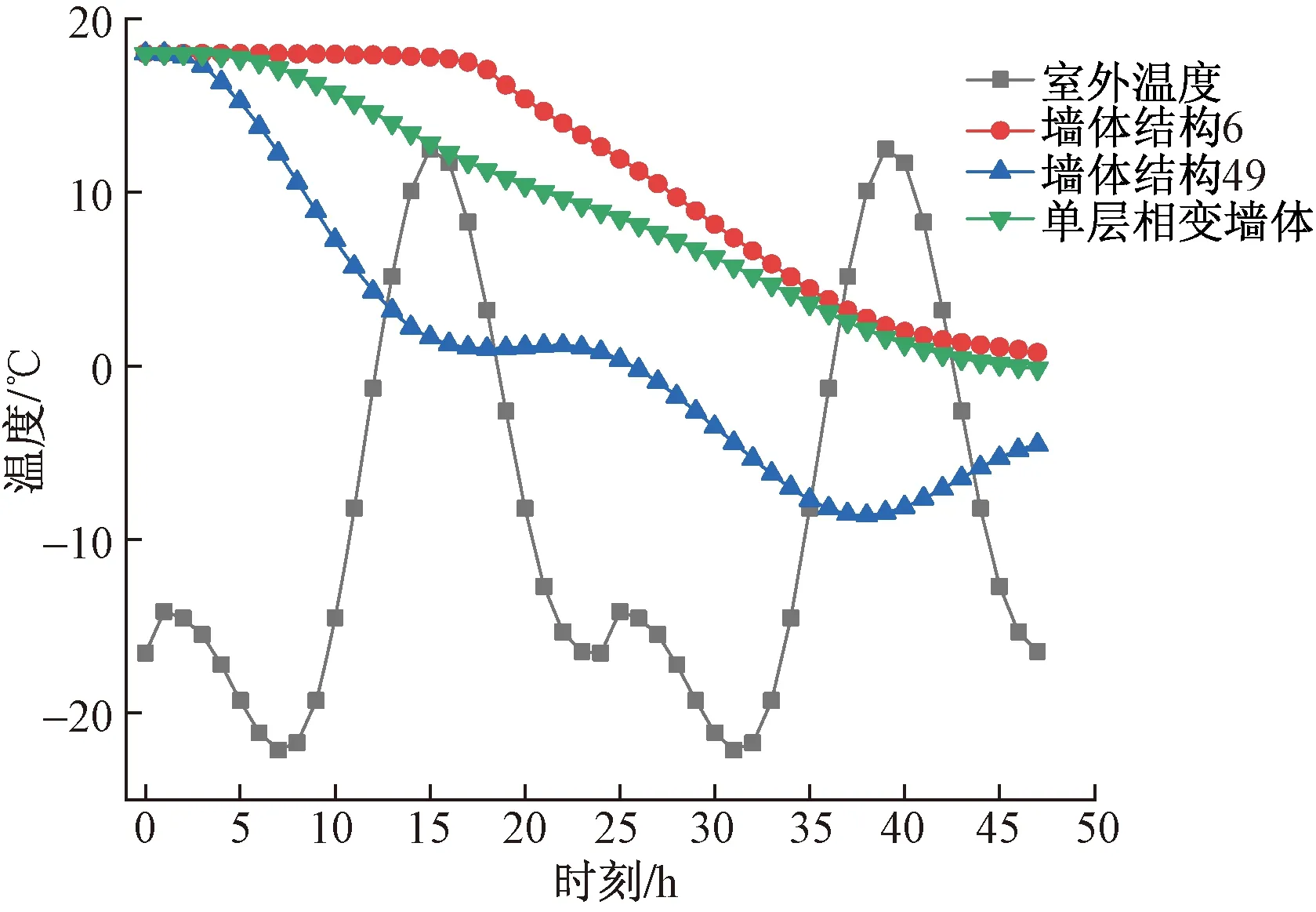
图6 西宁冬季双层定型相变墙体模拟结果Fig.6 Simulation results of the double-layer shaped phase change walls in Xining in winter

综上所述，西宁地区的双层定型相变墙体的优化组合可采取以促进冬季保温效果为主、夏季控制人体舒适性温度为辅的结构形式，并可主要通过冬季的保温效果来确定相变材料类型以及相变层厚度。

4 结论

以4种定形相变材料为相变保温层，构建了多种不同相变温度和厚度组合的双层定型相变墙体，通过建模及计算，模拟了双层定型相变墙体在夏热冬冷和寒冷地区的保温隔热效果，分析确定了不同气候分区的优化组合形式。主要结论如下。

(1)夏热冬冷和寒冷地区冬季的最佳相变保温层组合形式完全相同，夏季时夏热冬冷地区的保温隔热需求较高，相变层厚度较大，内侧相变材料的相变温度较高。

(2)相变材料层的厚度是影响墙体隔热保温效果的重要因素，双层相变材料形成的相变温度梯度在夏季表现出良好的隔热作用，对室内温度波动的控制效果较好。受所选用定形相变材料的相变温度和未考虑室内采暖措施的影响，相变墙体冬季的保温效果并不显著。

(3)双层定型相变墙体外侧相变材料的相变温度应接近并稍低于室外高温时段的环境温度平均值；内侧相变材料的相变温度以接近室内舒适温度为最佳。对于寒冷地区，外层可选取导热系数较低的相变材料增强冬季保温效果。