基于塔线体系的中冰区分裂导线断线响应分析
张 瑚,汪 峰,吕健双,柏晓路,李 萌
(1.中南电力设计院有限公司,武汉 430071;2.三峡大学土木与建筑学院,宜昌 443002)
架空输电线路长期暴露于野外,在风雨、冰雪等恶劣气象条件下线路容易覆冰断线[1]。断线产生的纵向不平衡张力是输电塔的重要设计荷载,线路发生断线后,会造成输电线路的振荡及相关电力设备的损坏,严重时会导致杆塔发生多米诺骨牌式地连续性倒塌以及其他次生灾害,进而引起整条线路瘫痪[2]。
目前,针对架空输电线覆冰断线问题,中外学者开展了广泛的研究。Campbell[3]推导了线路发生断线后的静力方程,得到了线路断线后的平衡位置和残余应力。Mozer等[4-5]根据简化线路模型推导出了线路发生断线时的峰值应力半解析公式,并通过3跨连续档输电线路缩尺模型,获得了不同断线工况下导(地)线发生断线时线路的峰值张力及残余静态应力的大小、杆塔各关键部位的应变等。Peyrot等[6]对试验线路进行了断线和绝缘子断串的试验研究,探讨了发生断线和断串后线路纵向荷载大小的变化情况。Thomas[7]开发了用于计算线路发生断线情况下绝缘子串和输电线路的应力时程程序。刘春城等[8]利用能量法建立了覆冰断线的冲击力学模型,发现断线冲击的动力响应大于未覆冰断线的情况。梁政平等[9]建立了以等效弹簧代替杆塔的“塔-弹簧”线路模型,以断线状态下悬挂点的支座反力反向施加于该模型上,分析了杆塔的动态响应。熊铁华等[10]对输电线路在遭受顺、横风向风荷载而发生断线时杆塔的失效模式进行了研究,提出了通过控制基本风压来寻找风荷载作用下输电塔失效模式的方法。
上述研究成果为输电导线覆冰断线效应研究奠定了坚实的基础。目前大多数学者集中于重冰区输电线覆冰断线研究,而基于塔线耦合体系的中冰区覆冰断线问题的研究相对较少[11-12]。另外,中国在特高压输电线路的设计和运行中,对整条输电线路的正常运营都会考虑输电线覆冰、断线效应[13],但现行的输电线路设计规范中,常是将输电塔与输电线分开来设计,未考虑塔线体系的耦合作用,且断线张力取值是依据拟静力法进行计算的,其计算结果偏向保守[14]。因此,现建立三档多分裂耐张段塔线体系有限元模型,对比分析不同断线工况时导线断线张力差静态稳定值和张力差动态峰值的变化规律,研究覆冰厚度、断线根数、绝缘子串长度、档数、断线位置等因素对于导线断线张力的影响规律,探索导线断线张力差动态峰值与静态稳定值的关系。以期为中冰区输电线路抗冰灾设计提供理论依据。
1 中冰区塔线体系覆冰断线模型
1.1 塔线体系断线理论
覆冰是输电线路面临的最严重的自然灾害之一,会导致导线重力荷载增大。与此同时,覆冰断线会造成导线的弹性势能迅速转化成动能,引起输电线路发生强烈振动。因此输电导线的断线运动过程可近似等效为初始能量为激励的振动问题[15],其动力学方程可采用振动微分方程:
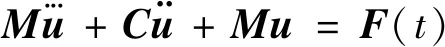
(1)

采用非线性瞬态动力学分析方法计算输电线覆冰断线,并确定输电导线覆冰断线作用下的断线张力变化。
1.2 塔线体系覆冰断线模型建立
研究对象为500 kV特高压交流三档四分裂耐张段线路,线路档距500 m,导线为JL/G1A-400/50型钢芯铝绞线,地线为JLB20A-100型铝包钢绞线,输电线机械参数如表1所示。导线张力取22 kN;地线张力取14.4 kN。直线塔高87.5 m,呼称高度81.0 m,横担长度42.67 m,底部根开17.07 m×17.07 m;其主材、横材、斜材以及输电塔顶部的横担均使用角钢,角钢材料型号有Q235和Q345两种型钢。绝缘子串为V型,间隔棒型号为JZFD4-45400,其质量为7.5 kg,悬垂联板型号为Lx-4245,线夹板结构是顶部宽0.5 m、底部宽0.45 m、高0.45 m的等腰梯形。中冰区覆冰厚度为15~20 mm、档距500 m、绝缘子串长6~12 m。
基于上述参数,首先利用ANSYS有限元软件建立三档多分裂耐张段塔线体系有限元空间模型,考虑荷载和阻尼的作用;然后进行输电线找形分析,并与理论分析进行对比。三档四分裂耐张段有限元模型如图1所示。
采用Beam188空间梁单元模拟输电塔塔杆,Beam188属于3D线性有限应变梁单元,适合分析较为细长的梁结构。为了提高解算的精度和速度,每个杆件划分3个单元,共计934个单元。杆件间的连接采用刚性连接。模型共使用29种角钢截面类型,角钢弹性模量E=2.1×1011Pa,密度ρ=7 850 kg/m3,泊松比ν=0.3,采用截面命令来定义不同角钢截面参数。采用Link10索单元模拟导线,该单元特点是只能承受轴向仅受拉或者仅受压,以此来模拟缆索或间隙等,每个节点上有3个自由度,它们具有应力刚化和大变形功能[16]。每根导线分别划分100个单元。

表1 导线的机械参数Table 1 Mechanical parameters of wire and ground

图1 三档四分裂耐张段塔线体系有限元模型Fig.1 Finite element model ofthree span tower-line system with four bundle conductor
为了反映工程实际,模型还考虑了绝缘子串和悬垂联板等金具的影响。绝缘子串有限元模型如图2所示。采用Beam4单元模拟绝缘子串,串长6~12 m,截面积为0.025 m2,弹性模量为2.0×1011Pa,泊松比为0.3。悬垂联板型号为Lx-4245,重量约37.86 kg,将其简化边长为0.45 m正方形,采用beam4模拟悬垂联板,截面积为0.025 m2,弹性模量为2.0×1011Pa,泊松比为0.3。
塔线体系模型构建完成后,采用张力迭代方法进行导线找形分析,并与悬链线理论值进行对比分析[17],如表2所示。
由表2可知,ANSYS计算值与悬链线计算值基本吻合,导线的弧垂最大误差仅为0.5%。

图2 V字型绝缘子串有限元模型Fig.2 Finite element model of V-shaped insulator string

表2 找形计算结果对比Table 2 Results of finite element and catenary
1.3 导线覆冰模拟及阻尼设置
目前输电线覆冰模拟有附加集中力法、附加单元法以及改变密度法。采用附加单元法模拟覆冰荷载,假设每档导线表面均匀覆冰,覆冰导(地)线分别划分100个单元。覆冰单元荷载计算公式为
W=ρgπb(D+b)×10-6
(2)
F=WL/n
(3)
式中:W为单位长度导线覆冰质量,kg/m;F为单元覆冰荷载,N;ρ为覆冰密度,单位为900 kg/m3;g为重力加速度,N/kg;D为导线外径,mm;b为覆冰厚度,mm;L为导线档距,m;n为单元个数。
覆冰模拟完成后,采用EKILL命令配合DELTIM命令设置荷载子步后杀死覆冰单元,实现导线脱冰模拟。由于输电线脱冰属于非线性问题,可以利用ANSYS的瞬态分析来解决。通过TIMINT命令打开瞬态效应,然后在利用TRNOPT命令定义method=full为完全瞬态分析法,采用KBC命令设置KEY=1为阶跃荷载,OUTRES命令输出求解选项。导线的临界阻尼系数取10%,不考虑β1刚度阻尼影响。
1.4 塔线体系模态对比分析
1.4.1 输电塔模态
采用子空间法来提取模态分析的前六阶振型,该方法的特点是适合于中型到大型的模型且振型相对较少,一般小于40阶。研究输电塔的固有频率和振型等动力特性,检验模型建立是否正确。其频率值如表3所示,部分振型如图3所示。
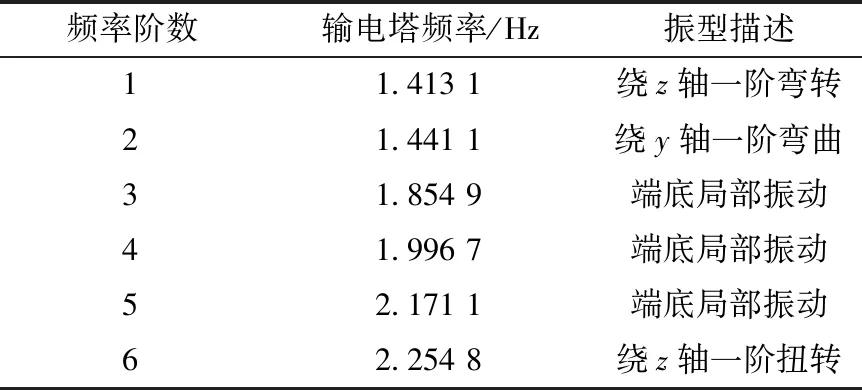
表3 输电塔的前6阶频率Table 3 The first 6 frequencies of the transmission tower

图3 单塔前两阶振型Fig.3 The first two modes of transmission tower
1.4.2 塔线体系模态
采用子空间法来提取模态分析的前六阶振型。研究塔线体系的固有频率和振型等动力特性,检验模型建立是否正确。对该三档四分裂耐张段分裂导线模型模态进行计算,其频率值如表4所示,部分振型如图4所示。

表4 塔线体系前6阶频率Table 4 The first 6 frequency of tower line system
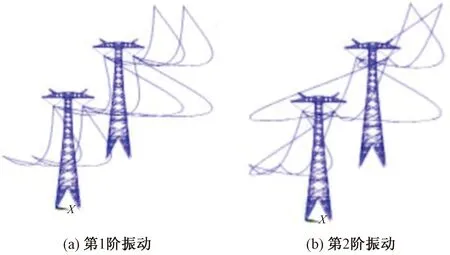
图4 塔线体系前两阶振型Fig.4 The first two modes of the tower line system
由表3和表4可知,塔线体系结构前6阶频率比单塔模型小。由图3和图4可知,塔线体系模型的低阶振型主要表现为导线振型。这是由于输电线刚度远小于输电塔,塔线模型的低阶振型仅能观察到导线的位移,输电塔变化微弱。
1.5 模型验证
利用文献[18]的算例数据,采用本文断线建模方法,构建试验塔线有限元模型,分析中不考虑导线与地面接触影响。通过断线瞬态分析,得到不同断线工况第3档导线张力差静态值及动态峰值,并与试验值进行比较,结果如表5所示。
由表5可知,本文建模方法的计算结果与试验结果基本吻合。导线断线张力差静态稳定值最大误差1.5%,导线断线张力差动态峰值最大误差8.5%,验证本文断线模拟方法的正确性。
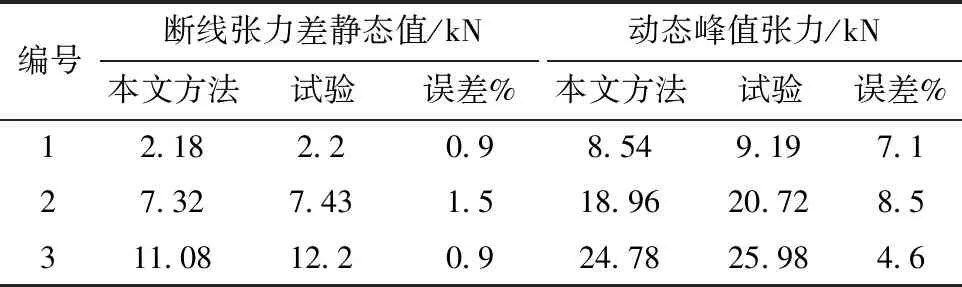
表5 断线张力差对比Table 5 Breaking tension comparison
2 中冰区导线断线张力因素分析
为了掌握中冰区输电线路覆冰断线效应的变化规律,开展分裂导线断线后张力差静态稳定值和张力差动态峰值对比分析,明确现行设计规范中的断线张力取值的合理性。
2.1 覆冰厚度与断线根数
三档四分裂耐张段每档的档距为500 m,V型绝缘子串长6 m,断线位置为导线和绝缘子串连接处,分别计算覆冰15~20 mm,导线断1~4根工况下的断线后张力差静态稳定值。不同覆冰厚度和断线根数条件下,导线的断线张力差静态稳定值变化图,如图5(a)所示。塔线体系一旦发生断线,输电塔会受到冲击作用,导致输电塔承受的纵向不平衡张力放大,即断线动力响应放大。该动力响应峰值通常大于规范规定的静力计算值,可能造成输电塔杆件破坏。覆冰15~20 mm,导线断1根和断4根产生的断线动张力值变化如图5(b)和图5(c)所示。
由图5(a)可知,当输电线覆冰厚度一定时,随着断线根数的增加,导线对应的断线张力呈非线性增大趋势,覆冰15 mm时,断1根导线的断线张力为8.745 kN,断4根导线的断线张力为102.905 kN,当导线断线根数一定时,断线张力随覆冰厚度的增大而不断增大。当断线根数为4,覆冰15 mm和覆冰20 mm的断线张力分别是102.905 kN和128.57 kN。
由图5(b)可知,四分裂导线断1根子导线时,导线张力差呈现振荡衰减趋势,且随着覆冰厚度的增加,断线张力振荡幅值逐渐增大,在13.55 s时刻断线张力差达到峰值。覆冰15 mm和覆冰20 mm的断线张力差动态峰值分别是13.89 kN和17.59 kN。由图5(c)可知,四分裂导线全断时,随着覆冰厚度的增加,断线张力幅值逐渐增大,在1.57 s,不同覆冰厚度工况下的断线张力时程曲线达到峰值,覆冰15 mm和覆冰20 mm的断线张力差动态峰值分别是309.3 kN和332.29 kN。由此可见,覆冰厚度越大,断线根数越多,导线断线时断线张力差越大。

图5 不同覆冰时四分裂导线断线张力差变化Fig.5 Breaking tension of four bundle conductor under different icing conditions
2.2 绝缘子串长度
以档距为500 m三档四分裂耐张段为例,V型绝缘子串长设置为6、8、10、12 m,导线覆冰20 mm,断线位置为导线和绝缘子串连接处,分别计算在不同绝缘子串长度下导线断1~4根工况下的断线静张力。导线断线张力差静态稳定值变化如图6(a)所示,张力差动态峰值变化时程如图6(b)所示。
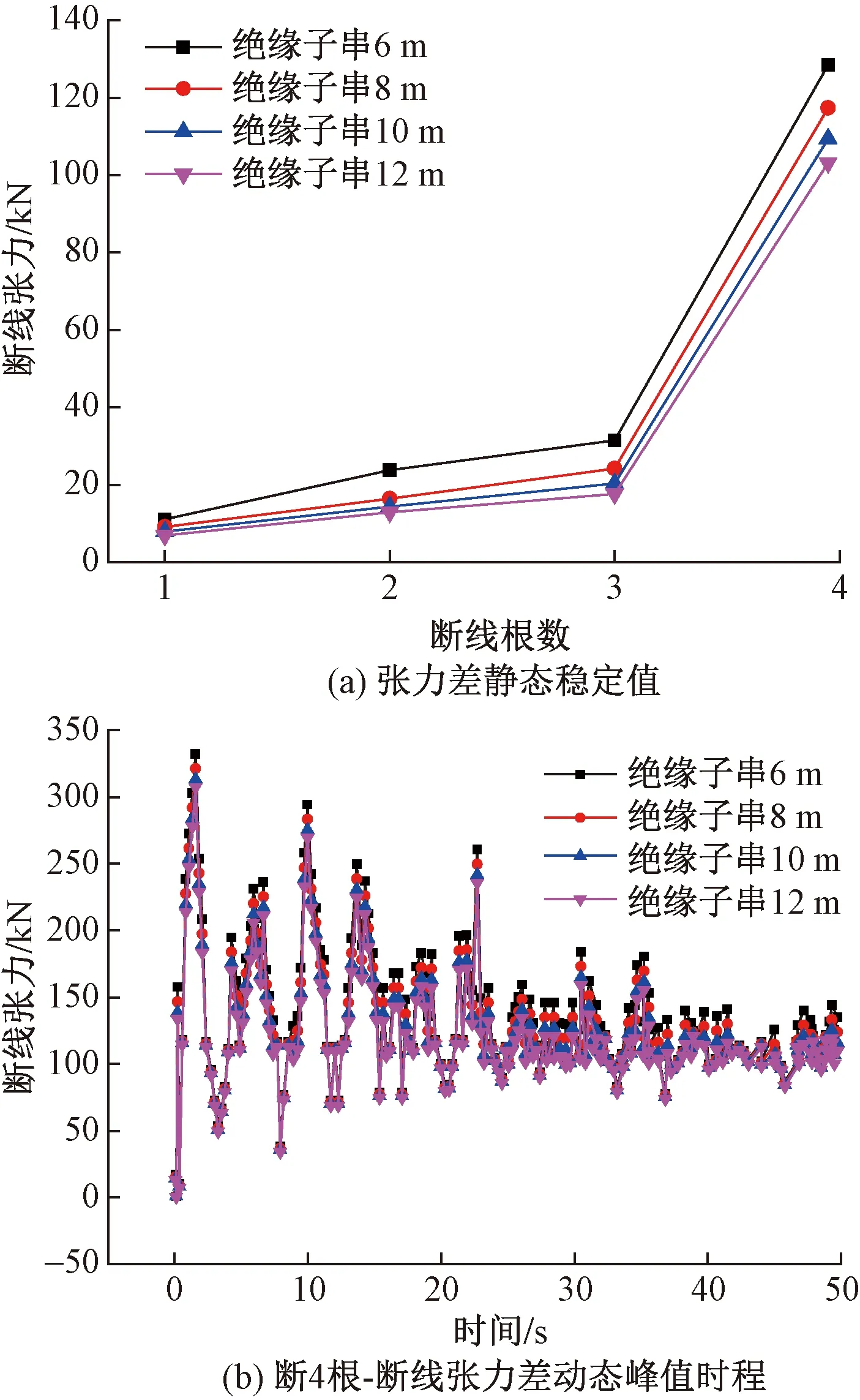
图6 不同串长时四分裂导线断线张力差变化Fig.6 Breaking tension of four bundle conductor withdifferent string length
由图6(a)可知,绝缘子串长度一定时,随着断线根数的增加,导线对应的断线张力差静态稳定值呈非线性增大趋势。绝缘子串长度为6 m时,断1根导线的断线静张力为11.096 kN,断4根导线的断线静张力为128.57 kN。导线断线根数一定时,断线静张力随绝缘子串长度的增大而不断减小。
由图6(b)可知,随着绝缘子串长度的增加,断线张力差动态峰值逐渐减小。在1.57 s时刻,断线动张力达到峰值,绝缘子串长6 m和绝缘子串长12 m的断线动张力峰值分别是332.3 kN和307.28 kN。由此可见,相同条件下,绝缘子串长度越长,导线断线静态张力差和动态张力差峰值越小。
2.3 档数
该工况为档数分别为3、5、7档耐张段,中档断线后一侧的剩余档数分别为1、2、3档,档距为500 m,V型绝缘子串长6 m,导线覆冰20 mm,断线位置为导线和绝缘子串连接处,分别计算不同档数下中档导线断1~4根工况下的断线静张力。不同档数条件下导线断线张力差静态稳定值变化如图7(a)所示。张力差动态峰值变化如图7(b)所示。
由图7(a)可知,20 mm覆冰情况下,当档数一定,随着断线根数的增加,导线对应的断线静张力不断增大,三档时,断1根导线的断线张力为10.971 kN,断4根导线的断线静张力为128.57 kN,当导线断线根数一定时,断线静张力随剩余档数的增大变化很小,断线根数为4时,3档和7档的断线静张力分别是128.57 kN和137.42 kN。

图7 不同档数条件下导线断线张力差变化Fig.7 Breaking tension of four bundle conductor with different span
图7(b)可知,随着档数的增加,断线动张力逐渐增大,但涨幅很小。在1.57 s时,不同档数工况下的断线动张力达到峰值,3档和7档的断线动张力峰值分别是332.295 kN和349.515 kN。由此可见,塔线体系的档数越大,导线断线张力呈现增大趋势,但增幅较小。
2.4 断线位置
以档距为500 m三档四分裂耐张段为例,V型绝缘子串长设置为6 m,导线覆冰20 mm,断线位置为中档导线距端部0 m(断点1)、125 m(断点2)和250 m(断点3)处,断线位置示意图如图8(a)所示。计算在不同断线位置下导线断1~4根产生的断线静张力。不同断线位置条件下导线的断线静张力变化如图8(b)所示,导线断4根的断线动张力变化如图8(c)所示。

图8 不同断线位置条件下导线断线张力差变化Fig.8 Breaking tension of four bundle conductor with different position
由图8(b)可知,20 mm覆冰情况下,当断线位置一定时,随着断线根数的增加,导线对应的断线静张力呈非线性增大趋势,断线位置为断点1时,断1根导线的断线静张力为10.971 kN,断4根导线的断线静张力为127.711 kN,当导线断线根数一定时,断线静张力随断线位置由断点1到断点3的变化而不断减小。当断线根数为4,断线位置为断点1和断点3的断线静张力分别是127.711 kN和93.884 kN。图8(c)可知,随着断线位置由断点1~断点3的改变,断线动张力逐渐减小,在1.57 s,不同断线位置工况下的断线动张力达到峰值,断点1和断点3的断线动张力峰值分别是332.3 kN和299 kN。
由此可见,断线位置由端部向跨中变化,导线断线张力越小。
3 不同方法计算断线张力对比
为了对比规范、曲线法、静力法和动力法对断线张力计算的差异性,不同方法计算的断线张力对比结果如图9所示。计算工况为三档四分裂耐张段档距500 m,绝缘子串长度6 m,无覆冰,断线位置为中档端部。

图9 不同方法计算断线张力对比Fig.9 Comparison of different methods
由图9可知,断线导线动张力计算,需要考虑动力放大效应。按照规范的静力方法,计算的导线断线张力大于曲线法和本文研究的有限元静力计算结果。但是,规范计算值、曲线法和有限元静力计算结果均小于考虑动力放大效应时的导线断线动张力峰值。
选取不同电压等级12种不同类型分裂导线,包括四分裂500/45、400/50、630/45、720/50、900/75型导线、六分裂400/50、500/45、1000/80、1250/100型导线、八分裂630/45、900/75、1250/100型导线,分别计算了不同覆冰厚度、档距、绝缘子串长时导线张力差,计算结果如图10所示。
由图10可知,分裂导线断一半的张力差动态峰值和静态稳定值之间呈现一定的线性关系,两者的比例系数约为1.69,分裂导线全断时的张力差动态峰值和静态稳定值之间也呈现一定的线性关系,两者的比例系数约为2.26,但是全断时的张力差动态峰值和静态稳定值的比例并不相同。分裂导线全断时,张力差的动态峰值比例大于断线一半时的张力差动态峰值。

图10 分裂导线全断时静态稳定值和动态峰值关系Fig.10 Relationship between static stable value and dynamic peak value of bundled conductor under full break
4 结论
建立了中冰区输电塔线体系断线数值模型,研究了覆冰厚度、断线根数、绝缘子串长度、档数、断线位置等因素对于导线断线张力的影响规律,结论如下。
(1)给出的塔线体系覆冰断线建模方法是正确的,可用于中冰区输电线路覆冰断线动力效应研究。塔线体系前10阶频率比单塔模型小,塔线模型的低阶振型主要表现为导线的振型。
(2)分裂导线断线时,导线不平衡张力差呈现振荡衰减趋势。塔线体系覆冰时,覆冰厚度越大,分裂导线断线根数越多,导线断线不平衡张力差越大;塔线体系的档数越大,导线断线张力呈现增大趋势,但增幅较小;绝缘子串长度越长,断线张力越小;断线位置由跨中向端部变化,断线张力越大。
(3)中冰区塔线体系覆冰断线导线动张力计算,需要考虑动力放大效应。多分裂导线全断时的张力差动态峰值和静态稳定值之间呈现一定线性关系,两者的比例系数约为2.26。

