政府干预下的本国与外国科技合作演化博弈研究

龙利娟， 王源昌， 吕 蕾

(云南师范大学 数学学院， 昆明 650500)

“坚持开放创新，加强国际科技交流合作”[1]是中国推动科技创新的重要举措。自古以来，人类社会的每一项进步,都伴随着科学技术的进步。随着信息化与科技全球化时代的到来，新一轮科技革命和产业变革蓬勃兴起，国际科技合作也将面临全新的机遇和挑战。

对于不同国家之间的科技合作，张公一等[2]分析了完全信息与参与者完全理性情形下不同国家间的静态博弈，但由于在研究不同国家之间的科技合作时，每个国家选择合作的概率属于一个动态变化过程，且在现实世界中，不同国家之间的合作处于不完全信息与有限理性状态中，则可以运用演化博弈的方法来刻画不同国家之间的动态科技合作关系。

就演化博弈而言，1973年Smith[3]首次提出的演化稳定策略标志着演化博弈理论的诞生，在此基础上，研究人员将其应用于多个领域。在应用研究领域，国内学者运用其基本原理对环境保护、电子商务、监管机制及机会主义行为研究等领域进行了积极的探索[4-5]。其中，就国际合作而言，郑军等[6]分析了中国与海上丝绸之路沿途国家合作的演化方向及其实现条件。除此之外，杨文珂等[7]研究了跨国绿色创新国家合作中机会主义行为治理机制以及如何抑制机会主义相关问题。

对于加入政府控制因素下的演化博弈研究，台德艺、潘海兰[8]研究了政府影响力与执行力对电商平台与经营者演化博弈中的影响；李林等[9]将政府作为一个市场主体，研究有无政府干预情况下的国家及高校和科研机构协同创新合作的演化博弈规律；李柏洲等[10]构建了“政府-国家-用户”三方演化博弈模型用以研究政府的政策激励对国家与用户创新知识交互中的作用；李玮等[11]基于外部性理论分别研究了有无政府激励政策下的私人参与基础设施融资行为选择问题；杨文珂等[7]在研究跨国绿色创新国际合作时，引入政府监管系数，对合作中的机会主义进行相应的惩罚。

本文在现有的研究基础上，选取了内生能力系数、科技合作成本系数、科技合作收益系数、“搭便车”收益系数、外部影响系数、合作风险系数、信任水平及政府干预力度系数共8个影响合作因素系数，全面分析了影响本国与外国科技合作的因素，并基于现实可能性，考察政府干预力度时，无法调控外国对其本国的干预力度，即本文只考虑政府干预力度对跨国科技合作的影响。同时，为研究方便，假定各国科技合作成本或收益为科技创新投入成本的线性函数。在此基础上，构建非对称演化博弈支付矩阵，建立动态方程，寻求不同条件下的演化稳定策略，并研究如何控制影响中国与其他国家科技合作的因素来促进两国之间的合作。最后，基于上述研究，利用2019年中国与越南各类别数据，进行博弈策略分析，对如何提高两国合作概率提供建议。

1 科技合作演化博弈模型的构建

1.1 博弈情形分析

对于政府干预下的本国与外国科技合作演化博弈研究而言，为了研究便利，对本国与外国科技合作策略问题做离散化假设，即{合作，不合作}二分法策略。将本国记为国家M，外国记为国家N，基于有限理性理论，在科技合作博弈问题中，本国与外国存在以下几种博弈情形：

1)双方均采取合作策略。国家M与国家N基于相互信任，在科技合作过程中双方收益均大于科技合作所需成本，则博弈双方在各自独立科研、自主创新的基础上，采取科技合作策略，在合作中将获得超额收益。

2)一方采取合作策略，另一方采取不合作策略。对于国家M而言，当其发现采取合作策略收益大于成本或在政府干预下不得不采取合作策略时，外国国家N发现其采取合作策略其收益小于所需成本或采取不合作策略将会具有“搭便车”收益，即在跨国科技合作中，国家之间存在信息不对称现象，当某一国选择合作时，将会产生一定的技术溢出，此时博弈中另一个国家有可能产生机会主义心理，从而出现“搭便车”现象，产生“搭便车”收益。此时国家M将采取合作策略，国家N将采取不合作策略；当国家M发现在政府控制下其采取合作策略收益小于成本或发现有机会获得“搭便车”收益，国家N发现采取合作策略其收益大于成本时，国家M将采取不合作策略，国家N将采取合作策略。

3)双方均采取不合作策略。由于在科技合作中，博弈双方均认为没有利益可得或均想采取“搭便车”行为，以及双方缺乏相互信任等原因而放弃合作，则国家M与国家N均采取不合作策略。

1.2 博弈收益矩阵的建立

假设博弈双方参与者之间存在足够多的合作机会，每一阶段博弈收益无差别，且在本文中，为研究方便，将以国家独立研究发生的成本为基石，利用某个参数与研究成本乘积来表示其他收益或成本，基于此建立国家M与国家N二分法策略下的不对称博弈收益矩阵，见表1。

表1 博弈双方收益矩阵

2 科技合作演化稳定点

2.1 复制动态方程及均衡点

基于上文分析，假设国家M选择合作的概率为x，选择不合作的概率为1-x，国家N选择合作的概率为y，选择不合作的概率为1-y。

由演化博弈理论，国家M选择“合作”策略与“不合作”策略的期望函数分别为

EM合作=y[αMCM+γMCM+μNMCM-βMCM-(1-ηMN)δMγMCM+mMCM]+(1-y)(αMCM+μNMCM-βMCM+mMCM)

(1)

EM不合作=y(αMCM+μNMCM+ρMCN-mMCM)+(1-y)(αMCM+μNMCM-mMCM)

(2)

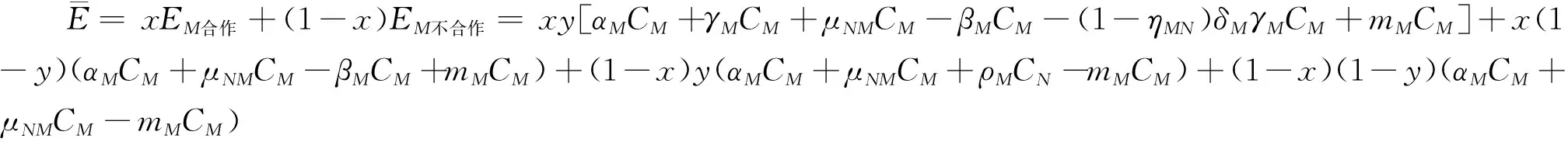
(3)

同理可得国家N选择“合作”策略与“不合作”策略的期望函数分别为

UN合作=x[αNCN+γNCN+μMNCN-βNCN-(1-ηNM)δNγNCN]+(1-x)(αNCN+μMNCN-βNCN)

(4)

UN不合作=x[αNCN+μMNCN+ρNCM]+(1-x)(αNCN+μMNCN)

(5)

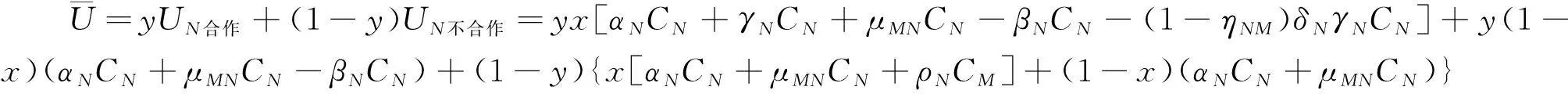
(6)

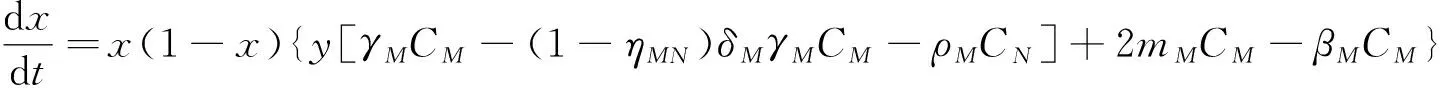
(7)

同理，国家N采取合作策略的复制动态方程为

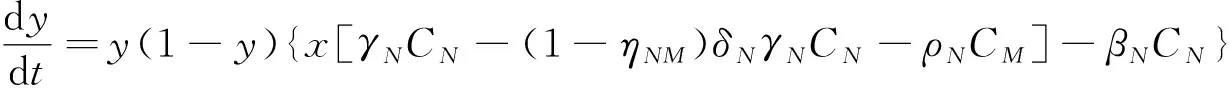
(8)

令

可以得到博弈的局部均衡点分别为O(0,0)、A(0,1)、B(1,0)、C(1,1)、D(x*,y*)。其中

为进一步对5个局部均衡点的稳定性进行分析，并对其合作演化路径进行分析，将根据博弈复制动态方程的雅克比矩阵进行下一步的分析。令

则雅克比矩阵为

其中，

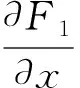
2.2 模型稳定性分析

情形1：2mM<βM。

条件1：

在此情形下，对于O(0,0)而言，其雅克比行列式

雅克比矩阵的迹为

trJ=-βNCN+(2mMCM-βMCM)<0。

对于A(0,1)而言，其雅克比行列式为

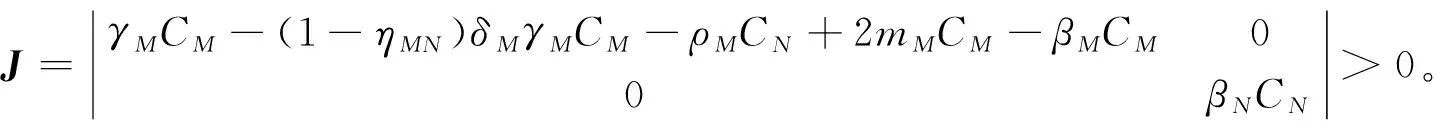
雅克比矩阵的迹为

trJ=βNCN+[γMCM-(1-ηMN)δMγMCM-ρMCN+2mMCM-βMCM]>0。

对于B(1,0)而言，其雅克比行列式为

雅克比矩阵的迹为

trJ=(-2mMCM+βMCM)+[γNCN-(1-ηNM)δNγNCN-ρNCM-βNCN]>0。

对于C(1,1)而言，其雅克比行列式

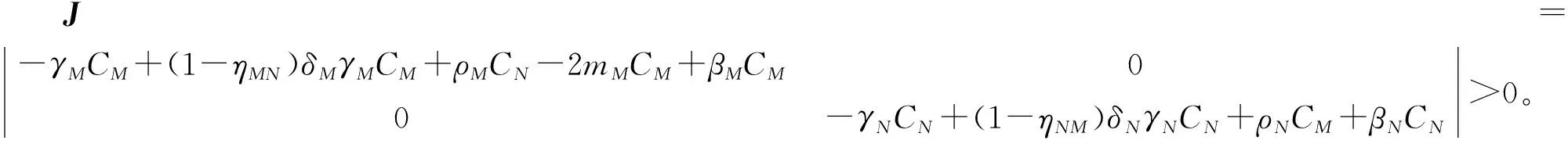
雅克比矩阵的迹为

trJ=[-γMCM+(1-ηMN)δMγMCM+ρMCN-2mMCM+βMCM]+[-γNCN+(1-ηNM)δNγNCN+ρNCM+βNCN]<0。

对于D(x*,y*)而言，其雅克比行列式为

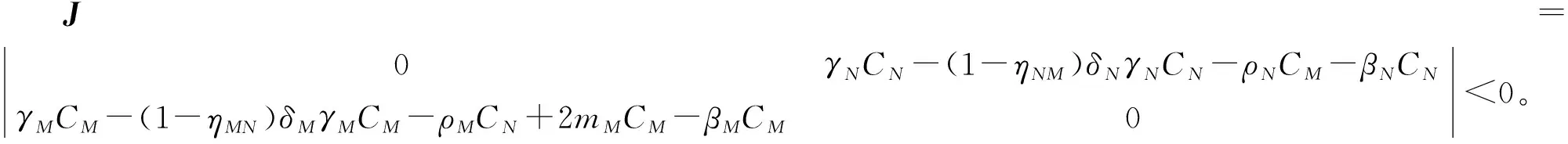
雅克比矩阵的迹为

trJ=0。

由Friedman[12]所提出的雅克比矩阵判别均衡点稳定性分析可得系统的稳定策略见表2，在此条件下演化博弈系统存在5个均衡点，分别为O(0,0)、A(0,1)、B(1,0)、C(1,1)、D(x*,y*)，其中O(0,0)、C(1,1)具有局部稳定性，称为局部稳定点，演化稳定策略为(不合作，不合作)与(合作，合作)。A(0,1)、B(1,0)为不稳定点，D(x*,y*)为鞍点。在此条件下，对国家M而言，当国家N以固定概率y*选择合作，则当其选择合作概率xx*时，国家M选择合作策略所得收益将大于其选择不合作策略所得收益,此时国家M将会选择合作策略。同理而言，对于国家N，当国家M以固定概率x*选择合作，则当其选择合作概率yy*时，国家N选择合作策略所得收益将大于其选择不合作策略所得收益，此时国家N将会选择合作策略。

表2 情形1下条件1中均衡点稳定性分析

条件2：

在此条件下，系统稳定策略见表3，演化博弈系统存在5个均衡点，分别为O(0,0)、A(0,1)、B(1,0)、C(1,1)、D(x*,y*)，其中O(0,0)具有局部稳定性，称为局部稳定点，演化稳定策略为(不合作，不合作)，A(0,1)为不稳定点，B(1,0)、C(1,1)、D(x*,y*)为鞍点。在此条件下，由于国家N选择合作的收益会小于其选择合作的风险与成本及其采取“搭便车”所带来的收益之和，则国家N一定会选择不合作策略，在此情形下，国家M由于一开始选择合作的收益大于其所需付出的代价，则在开始时选择合作策略，但当其发现收益越来越低，直至其超过成本时，国家M会改变其策略，选择不合作策略，即就其长时间博弈而言，最终国家M与国家N都会选择不合作策略。

表3 情形1下条件2中均衡点稳定性分析

条件3：

在此条件下，系统稳定策略见表4，演化博弈系统存在5个均衡点，分别为O(0,0)、A(0,1)、B(1,0)、C(1,1)、D(x*,y*)，其中O(0,0)具有局部稳定性，称为局部稳定点，演化稳定策略为(不合作，不合作)，B(1,0)为不稳定点，A(0,1)、C(1,1)、D(x*,y*)为鞍点。在此条件下，由于国家M选择合作的收益会小于其选择合作的所需付出的代价，则国家M一定会选择不合作策略，在此情形下，国家N即使选择合作的收益大于合作的风险与成本及其采取搭便车所带来的收益之和，在开始时选择合作策略，但就其长时间博弈而言，最终国家M与国家N都会选择不合作策略。

表4 情形1下条件3中均衡点稳定性分析

条件4：

在此条件下，系统稳定策略见表5，演化博弈系统存在5个均衡点，分别为O(0,0)、A(0,1)、B(1,0)、C(1,1)、D(x*,y*)，其中O(0,0)具有局部稳定性，称为局部稳定点，演化稳定策略为(不合作，不合作)，C(1,1)为不稳定点，A(0,1)、B(1,0)、D(x*,y*)为鞍点。在此条件下，由于国家M选择合作的收益会小于其选择合作的所需付出的代价，当国家M采取合作策略时，其必定希望通过此策略从合作过程中获得额外收益，而对于国家N而言，其选择合作的收益同样小于合作的风险与成本及其采取“搭便车”所带来的收益之和，同理而言，其同样希望通过合作来获得额外收益，则博弈双方在开始时都会选择合作策略，以期在其中获得收益，但其均衡状态属于劣势均衡状态，双方虽实现短期利润增加，就其长时间博弈而言，最终国家M与国家N都会趋向于不合作策略。

表5 情形1下条件4中均衡点稳定性分析

情形2：2mM>βM。

条件1：

在此条件下，系统稳定策略见表6，演化博弈系统存在5个均衡点，分别为O(0,0)、A(0,1)、B(1,0)、C(1,1)、D(x*,y*)，其中C(1,1)具有局部稳定性，称为局部稳定点，演化稳定策略为(合作，合作)，A(0,1)为不稳定点，O(0,0)、B(1,0)、D(x*,y*)为鞍点。在此条件下，对于国家N而言，其选择合作的收益大于合作的风险与成本及其采取搭便车所带来的收益之和，则其趋向于选择合作策略，而对于国家M而言，与情形1下条件1相比(此时mM>0，即政府采取奖励政策)，政府奖励力度加大，且其收益大于成本，则其选择合作策略速度加快，国家M更倾向于选择合作策略。即在博弈最后，国家M与国家N都会选择合作策略。

表6 情形2下条件1中均衡点稳定性分析

条件2：

在此条件下，系统稳定策略见表7，演化博弈系统存在5个均衡点，分别为O(0,0)、A(0,1)、B(1,0)、C(1,1)、D(x*,y*)，其中B(1,0)具有局部稳定性，称为局部稳定点，演化稳定策略为(合作，不合作)，A(0,1)，D(x*,y*)为不稳定点，O(0,0)、C(1,1)为鞍点。在此条件下，对于国家N而言，其选择合作的收益小于合作的风险与成本及其采取搭便车所带来的收益之和，则其趋向于选择不合作策略，其不合作策略为稳定策略，但对于国家M而言，由于其选择合作策略收益大于其选择合作所需成本，则其合作策略为稳定策略。在长时间的博弈中，国家M将会选择合作策略，国家N会选择不合作策略。

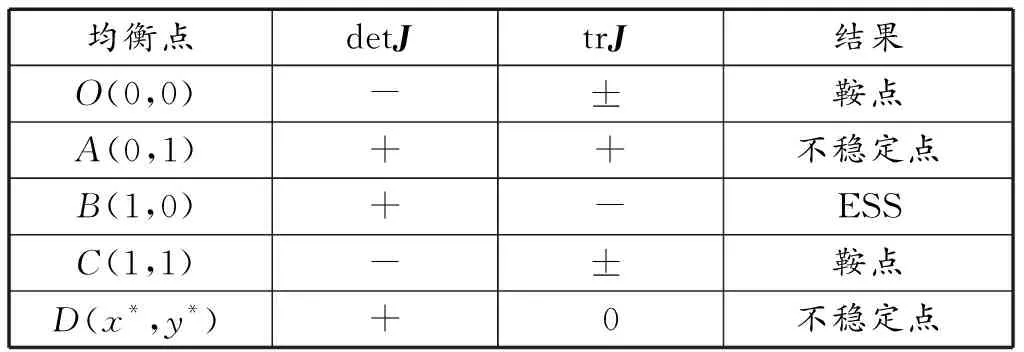
表7 情形2下条件2中均衡点稳定性分析

条件3：

在此条件下，系统稳定策略见表8，演化博弈系统存在5个均衡点，分别为O(0,0)、A(0,1)、B(1,0)、C(1,1)、D(x*,y*)，且均为鞍点。在此条件下，对于国家N而言，其选择合作的收益大于合作的风险与成本及其采取“搭便车”所带来的收益之和，则其趋向于选择合作策略，但对于国家M而言，虽然政府采取了一定的奖励政策，由于力度较小，导致国家M选择合作所得收益仍然低于其所需成本，即国家M更倾向于不合作，但此时，由于国家N选择合作策略，国家M获得“搭便车”收益，则国家N选择合作策略的概率将会降低， 同时，由于国家M知晓国家N的策略选择，国家M同样希望获得合作收益，即其选择合作的概率将会上升，即在此时，两国家之间的博弈不存在稳定均衡现象，两国家之间的策略选择将一直处于动态变化过程。

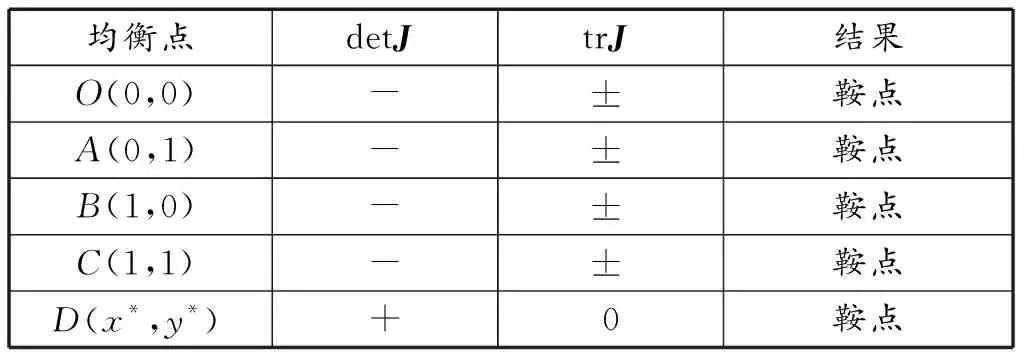
表8 情形2下条件3中均衡点稳定性分析

条件4：

在此条件下，系统稳定策略见表9，演化博弈系统存在5个均衡点，分别为O(0,0)、A(0,1)、B(1,0)、C(1,1)、D(x*,y*)，其中B(1,0)具有局部稳定性，称为局部稳定点，演化稳定策略为(合作，不合作)，O(0,0)、D(x*,y*)、A(0,1)为鞍点，C(1,1)为不稳定点。在此条件下，对于国家N而言，其选择合作的收益小于合作的风险与成本及其采取“搭便车”所带来的收益之和，则其趋向于选择不合作策略，对于国家M而言，即使其选择合作的收益小于其选择合作的所需付出的代价，但由于政府对其采取的奖励大于其所需的成本，则其将会选择合作策略。即最终在长时间的博弈中，国家M将会选择合作策略，国家N会选择不合作策略。

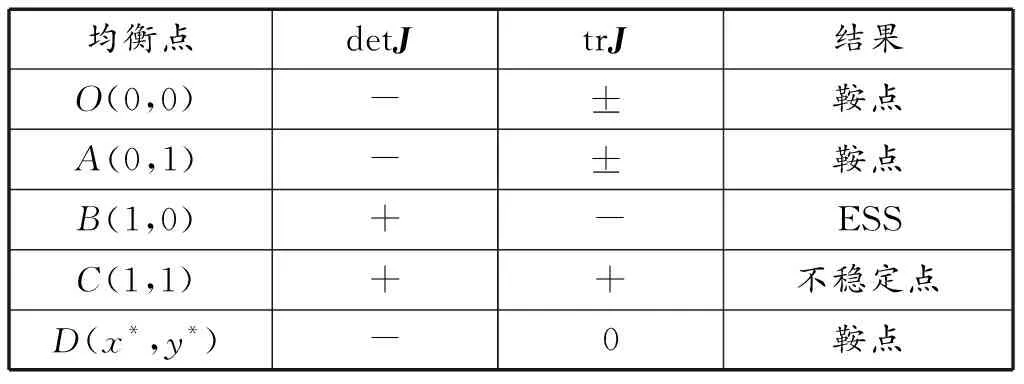
表9 情形2下条件4中均衡点稳定性分析

3 科技合作演化稳定性仿真

在以上分析中，在情形1下的条件2至条件4中，无论国家M与国家N选择合作的概率为多少，最终都会趋向于(不合作，不合作)策略，且在情形2中的4种条件下，皆为双方都选择合作或其中一方选择不合作，而对于情形1中的条件1而言，其均衡点为O(0,0)，C(1,1)，其更具有研究价值。考察在此情形下科技合作博弈模型中参与者的演化行为，各参数的取值为βM=1.2，βN=0.7，γM=3，γN=2，ηMN=0.6，ηNM=0.5，δM=0.3，δN=0.4，ρM=0.1，ρN=0.2，CM=10，CN=7，mM=0.2。仿真结果如图1所示。

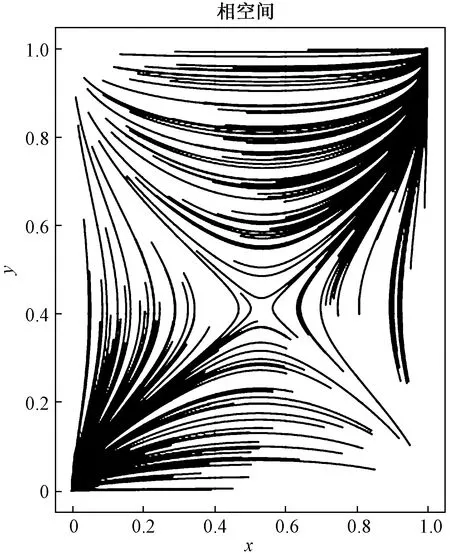
图1 情形1下条件1中的系统动态演化图

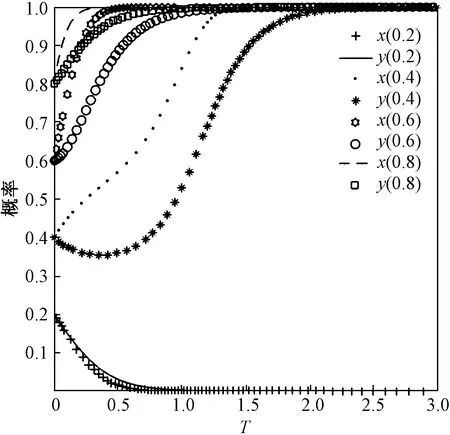
图2 不同初始概率下的系统演化轨迹

显而易见，参数的不同取值将会影响演化博弈系统的稳定性。在实际情况中，基于政府控制下，可控参数为βM与mM，则下文将研究在控制其余参数不变的情形下，分别改变βM与mM对系统稳定性的影响。

3.1 国家M合作成本系数βM对科技合作的影响

为考察不同程度的合作成本系数对国家M与国家N演化路径的影响，因此βM分别取值0.5、1.5、2.5，分析在国家M合作成本系数βM不同状况下的国家M与国家N演化行为的变化。观察图3可知，对于国家M而言，当βM=0.5与βM=1.5时，国家M向x=1的方向演化，且随着科技合作所需成本的增加，国家M越不可能采取合作策略；当βM=2.5时，国家M向x=0的方向演化，即当科技合作成本增长到一定程度时，国家M会将合作策略改变为不合作策略，对于国家N而言也同样如此，且在βM相同的情况下，国家M的策略选择将会影响国家N的策略选择，当国家M选择合作策略时，由于其能为国家N带来“搭便车”收益，则国家N也会随之选择合作策略，当国家M选择不合作策略时，即使对于国家N而言，其收益大于风险、成本与“搭便车”收益之和，但由于国家N无法从中获益，则其也会在国家M的策略影响下选择不合作策略。

图3 不同科技合作成本下的系统演化轨迹

3.2 政府对国家M是否进行合作采取的干预力度mM对科技合作的影响

为进一步讨论政府对国家M与国家N科技合作博弈中策略选择作用机理，考察政府采取怎样的干预力度来有效地推动中国与其他国家科技合作发展。在博弈过程中，固定其余参数不变，对于mM分别取值-0.5、-0.05、-0.015、0、0.5，观察图4可知，当mM=0时，代表政府不采取任何干预措施，即无政府干预情形下的跨国科技合作演化博弈，此时国家M与国家N将趋向于科技合作策略，但在mM>0时，即政府采取奖励政策时，相较于政府不采取任何措施而言，国家M收敛于x=1的速度加快，即其更乐于采取合作策略，并且在国家M的影响下，国家N也会采取合作策略，演化博弈系统收敛于(1,1)策略速度将加快，即政府采取奖励政策有利于推动国家M与国家N的科技合作；当mM<0时，即政府对国家M采取惩罚政策；当mM=-0.015时，国家M与国家N收敛于(1,1)策略，此时与政府不采取任何措施而言，国家M收敛于x=1的速度降低，并在此情况下，国家N在国家M的影响下，收敛于x=1的速度也降低；当mM=-0.5与mM=-0.05时，由图4显而易见，此时两国均倾向于不合作，且mM=-0.05时国家M与国家N收敛于(0,0)的速度明显低于mM=-0.5时的国家M与国家N收敛于(0,0)策略的速度，即当施加惩罚时，若惩罚力度越大，国家M选择不合作的时间越短，越倾向于不合作，同时，国家M的演化策略也会影响国家N策略的选择，使其同样将合作策略改变为不合作策略。

图4 政府不同干预力度下的系统演化轨迹

4 实证分析

2021年是中国与东盟建立对话关系30周年。在过去30年里，中国与东盟交流日益加深，2020年成为中国第一大贸易伙伴。据驻东盟使团经济商务处统计显示，2020年，中国与东盟贸易额同比增长6.7%。并且，随着RCEP在2020年11月15日的成功签订，中国与东盟之间的交流与联系将会日益扩大，因此研究中国与东盟各国之间的交流也越发重要。数据显示，越南为2020年中国在东盟的第一大贸易伙伴，分析中国与越南两国间的合作具有代表性意义。因此，本文着重研究中国与越南之间的科技合作。

在此情况下，为促使两国顺应全球化趋势，选择参与科技合作，由本文的模拟分析可在此基础上对科技合作成本进行控制，由于本文利用保护主义程度量化科技合作成本，则可通过降低两国保护主义程度进而降低科技合作成本。基于本文参数选择，可通过降低关税从而降低科技合作成本，这与2020年11月所提出的RCEP不谋而合。基于此，中国与越南应积极参与到RCEP中，积极遵守RCEP准则，从而提高两国科技合作概率。并且，由上文分析可知，也可通过政府控制促使两国家间进行科技合作。

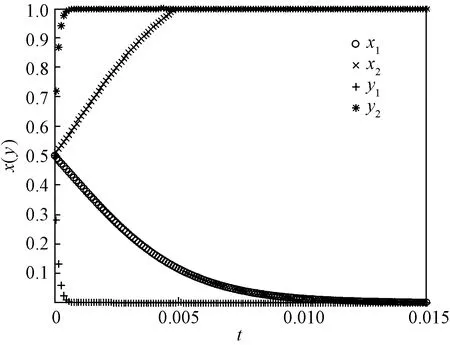
图5 中国与越南2019年科技合作演化博弈图

5 结论

基于演化博弈的思想构建了中国与其他国家科技合作策略选择的演化博弈模型，引入政府控制力度参数，对本国与其他国家的行为选择进行分析，并运用MATLAB软件进行模拟仿真，得出以下结论：

1)从长期来看，科技合作博弈策略选择处于动态变化中，是合作成本、政府干预力度、合作收益系数、合作风险、“搭便车”收益系数等因素共同作用的结果，且策略稳定均衡点受博弈双方参与者初始状态影响。

2)在本文模拟仿真的情形下，国家M的科技合作成本系数将影响国家M与国家N演化路径，科技合作成本越低，双方合作欲望越强烈，若科技合作成本超过某一阈值，将驱使博弈双方采取不合作策略；同时，政府对科技合作的干预力度也将影响国家M与国家N的演化路径，当政府采取奖励政策时，奖励力度越大，博弈双方参与者合作欲望越强烈；当政府采取惩罚政策时，当惩罚力度较小时，国家M发现相较于不合作，其选择合作所获收益更多，此时它将选择合作策略，但随着惩罚力度的加大，国家M发现利益减少，将会选择不合作策略，并影响国家N策略选择，此时博弈双方参与者均倾向于选择不合作策略，且惩罚力度越大，两国更不愿意选择合作。

基于当今复杂的世界环境，在复杂的国际关系中取得收益最大化是众多研究者长期以来所追寻的目标。本文基于近年来中国与东盟贸易、文化等方面合作交流日益加深，以中国与越南为例，实证分析跨国间科技合作情况，发现中国与越南2019年科技合作中两国均趋向于不合作。基于上文对两国间科技合作影响因子分析，为加强中国与越南间科技合作，提出以下建议：两国作为ACFTA与RCEP成员国，应把握住机遇，积极响应政策，降低关税以增强两国间合作程度，降低合作成本系数，从而促使两国加强科技合作。同时，中国作为世界上具有重要影响力的科技大国，政府应积极参与国际科技合作，对科技合作中的地区、企业、个人等加以有效策略干预，从而增强国际科技合作概率。

基于以上分析，本文建议：由于跨国科技合作博弈策略的选择受合作成本、政府干预力度、合作收益系数、合作风险、“搭便车”收益系数等因素的共同影响，则如何调整以上因素是推动跨国科技合作的重中之重。就政府而言，增大对本国参与者的奖励力度有助于促进国际科技合作；同时，采取有力措施降低科技合作成本也不可忽略。