转盘流道结构对网箱清洗装备喷嘴流场特性的影响

廖宇琦，袁太平，胡昱，王绍敏，陶启友，黄小华

(1上海海洋大学水产与生命学院，上海 201306；2 中国水产科学研究院南海水产研究所热带水产研究开发中心，海南 三亚，572000)

网衣清洗是深水网箱养殖管理的关键环节之一，空化射流网衣清洗装备作为有效解决深水网箱网衣污损生物严重附着问题的重要工程手段，已成为近年来的研究热点[1-4]。高压流经清洗装备分流转盘流道及喷嘴后，在喷嘴缩颈结构处发生空化效应而形成空化射流，空泡在网面持续破裂时伴随有大幅的激波和微射流产生，形成污损生物脱落的破碎力，从而实现网衣的清洗[5]。

数值模拟方法作为研究流道内部流场水力特性的重要手段，已广泛应用于各项机械工程领域[6-10]。胡国良等[11]利用Fluent软件对消防水炮炮身模型进行了模拟仿真，分析了炮身流道壁面的压力及出口速度分布情况。谢华等[12]采用数值模拟方法分析了肘形进水流道出口断面的流速分布和水力损失等指标，为实际加工选出最优方案。刘长誉等[13]利用Fluent软件模拟了不同阀口开度下液压阀内部流场压力、速度的分布，表明阀口开度增大，流场压力和速度梯度逐渐减小。Spence等[14]运用4种不同的湍流模型对曲率半径比为 1.3、5、20的弯管进行模拟，分析了各弯管的上下游压力分布、内外壁压力分布、速度场，结果表明，RSM模型可为不同曲率半径弯管提供准确的压力损失数据。付强等[15]采用RNGk-ε模型数值模拟肘型和簸箕型进水流道，表明肘型进水流道的水头损失比簸箕型进水流道小。朱登伟等[16]数值模拟了立柱内走油单双通道压力损失和流速变化，表明单通道流道压力损失最小，速度最大，可作为最优通道。综上所述，流道结构的变化对流道内流场的压力、速度、能量损失等因素有显著影响。目前国内外研究者主要针对消防水炮、大型水泵站、阀口等流道利用数值模拟方法展开研究，但在对深水网箱网衣清洗装备方面报道较少。

本研究采用基于计算流体力学(Computational Fluid Dynamics,CFD)数值模拟方法分析比较了直角L型流道和圆弧L型流道内部流场的变化，研究两种流道对喷嘴流场压强、速度、湍流动能和空化程度的影响，旨在为网衣清洗装备分流转盘流道结构优化提供理论依据。

1 材料与方法

1.1 材料

1.1.1 网衣清洗装备

网衣清洗装备是利用空化效应实现网衣清洗的水动力装置，主要由高压泵站、喷嘴、分流转盘、旋转接头、高压密封机构和螺旋桨推进器等部分组成。

空化射流网衣清洗装备实物图及结构示意图如图1、图2所示。

图1 网衣清洗装备实物图Fig.1 Physical picture of netting cleaning equipment

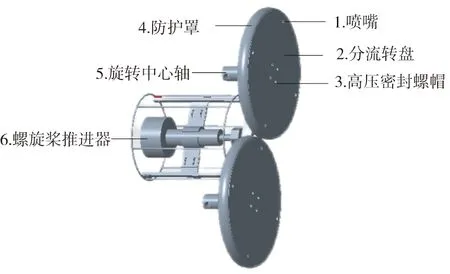
图2 空化射流网衣清洗装备结构示意图Fig.2 Schematic diagram of cavitation jet netting cleaning equipment

网衣清洗装备工作原理：高压泵站形成的高压流经旋转中心轴流入分流转盘流道，高压流经流道末端喷嘴形成高速射流，在喷嘴缩颈结构处形成涡流区域，涡流中心压力低于饱和蒸汽压力时，流体发生断裂形成空化效应，高速空化射流空泡持续破裂形成的破碎力可用于清除网面污损生物。射流反作用力形成对称力矩驱动分流转盘旋转，形成圆环形的高速射流轨迹，结合清洗装备的运动，从而实现整个网箱的清洗。螺旋桨推进器产生的反推力起到了使网衣清洗装备贴网的作用。

1.1.2 流道几何结构

研究对象为分流转盘内部流道，流道结构分为两种类型：直角L型流道和圆弧L型流道。直角L型流道弯曲段极角为 90 °，曲率半径为0 mm；圆弧L型流道曲率半径为 3 mm。两种流道长度均为 177 mm，流道直径均为 6 mm，流道末端与喷嘴垂直连接，喷嘴孔径为 1 mm，喷嘴长度为 3 mm，流道底部至喷嘴出口高度为 16 mm。为简化对L型流道内流体流场仿真模拟，作如下说明[17]：(1)将内径作为公称直径进行模拟产生误差较小，可忽略不计，内径近似认为公称直径；(2)流道在淹没状态下模拟，无气相和固相介质干扰；(3)将流道分为4个部分，分别为水平段、弯曲段、竖直段、喷嘴。水流从φ6 mm流道入口进入水平段，经过弯曲段进入竖直段，最后从φ1 mm喷嘴射出。定义流道弯曲段上侧为内侧，下侧为外侧，如图3所示。

图3 圆弧L型流道几何简图Fig.3 Schematic of Circular-arc L-shaped channel geometry

1.2 研究方法

1.2.1 流体运动方程

流体运动遵循质量守恒定律、牛顿第二定律以及能量守恒定律。流体流动过程中温度保持在恒温，热量传递少，可忽略不计，运动控制方程如下[18-19]：

(1)

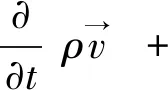
(2)

1.2.2 standardk-ε 湍流模型

standardk-ε模型中输运方程为[20-21]：

(3)

(4)

式中：k和ε是2个基本未知量，Gk是由于平均速度梯度引起的湍动能k的产生项，Gb是由于浮力引起的湍动能k的产生项，YM代表可压湍流中脉动扩张，C1ε、C2ε和C3ε为经验常数，σk和σε分别是与湍动能k和耗散率ε对应的普朗特(Prandtl)数，Sk和Sε是用户定义的源项。

第二个模型方程是基于现象提出而非推导得到的ε方程：

(5)

ε和K以及湍流长度尺度相关：

(6)

结合K方程,湍动黏度可以表示为:

(7)

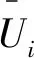
1.2.3 Mixture模型

在空化过程中，液-气传质由蒸汽输送方程控制：

(8)

Li等[22]提出Mixture模型基于两相连续方程，包括液相、气相和混合相的3组守恒方程，方程式如下：

液相：

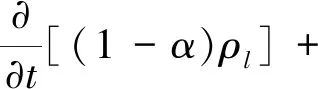
(9)

气相：

(10)

混合相：

(11)

混合相密度：

ρ=αρv+(1-α)ρl

(12)

混合相密度与气相体积分数的关系：

(13)

1.2.4 Zwart-Gerber-Belamri空化模型

Zwart-Gerber-Belamri提出利用气泡密度数n和单个气泡的质量变化率计算单位体积总界面传质率R，方程式如下[23]：

(14)

气相体积分数(α)与气泡数密度(n)和气泡半径(RB)的关系为：

(15)

气泡动力学方程表述为[22]：

(16)

(17)

气泡的增长过程(蒸发)方程如下：

(18)

空化模型的最终形式为[24]：

(19)

(20)

式中：F为经验校准系数；α为蒸气体积分数；αnuc为成核部位体积分数，5×10-4；Fvap为蒸发系数，50；Fcond为冷凝系数，0.001；Re表示蒸气发生源项；Rc表示冷凝速率源项；RB表示气泡半径，10-6m；PB表示气泡压强；Pv表示饱和蒸气压；ρv表示气体密度。

1.3 数值求解

1.3.1 模型建立

分流转盘内部流道直径较小，可忽略重力的影响，为方便计算，取二维模型作为研究对象。使用ANASYS Fluent中DM模块对流道进行建模，在Mesh模块中对流道进行网格划分，生成的网格为四边形结构化网格。为了提高计算结果的准确度，对流道与喷嘴连接处的网格进行了局部加密处理，直角L型流道和圆弧L型流道网格结构划分如图4a、图4b所示。

图4 两种流道网格划分图Fig.4 Two kinds of channels meshing diagrams

水力模型边界条件设置，求解工具采用Fluent求解器，采用standardk-ε模型模拟。入口、出口边界条件设置为压力边界，液体密度ρ=998.2 kg/m3，液体运动黏度v=0.001 003 m2/s，入口压力Pin=15 MPa，出口压力Pout=0.098 MPa，湍流强度5%，入口水力直径D=6 mm，出口水力直径D=1 mm。结构网格下离散格式选择Second Order Upwind，压力差值格式选择Second Order。速度场与压力场的解耦采用SIMPLE算法，使用Hybird Initialization进行初始化，求解计算。

空化模型边界条件设置，求解工具采用Fluent求解器，采用Mixture混合相模型和Zwart-Gerber-Belamri空化模型模拟。液体边界条件设置同上，气体密度ρ=0.025 58 kg/m3，气体动力黏度v=1.26×10-6Pa·s，环境压力PV=3.54 MPa，饱和蒸气压P=3.54 kPa。湍流强度5%，湍流黏度率10%。离散格式选择Second Order Upwind，压力差值格式选择Second Order。速度场与压力场的解耦采用SIMPLE算法，使用Hybird Initialization进行初始化，求解计算。

1.3.2 网格无关性和时间步长独立性验证

取圆弧L型流道喷嘴截面y轴速度分布进行验证。在图4的计算域中，监测y轴向速度变化。以流速作为监测对象，根据设置不同的网格单元尺寸、分度数等参数，设计4套网格方案，如表1所示，网格总数范围4 000～14 000，设置相同的计算模型与边界条件，结果如图5所示。

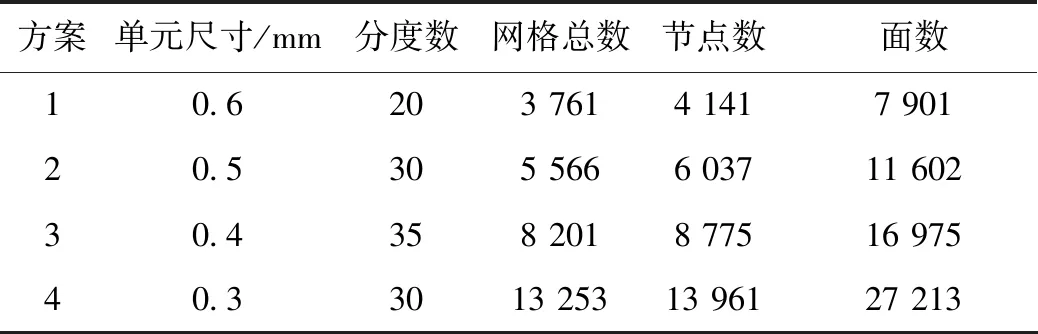
表1 网格计算方案Tab.1 Grid computation solution

图5 网格无关性验证结果图Fig.5 Result graph of grid independence verification

图5可知，方案1计算值的速度变化率稍低于其他3个方案计算值的速度变化率，方案2、方案3和方案4速度变化曲线基本重叠，速度变化率最大偏差小于0.59%。说明方案2、方案3和方案4网格计算结果近似达到稳定，综合考虑计算周期与计算精度，选择网格划分方案3[25]。直角L型流道网格划分同样采用此方法。

对于确定的网格方案，为满足计算域有足够的时间步长以确保结果的准确性，在每个时间段内采取不同的时间步长进行计算，并保证在时间间隔内计算次数必须迭代至收敛。时间步长分别设定为150、500、1 000、3 000。以y轴线速度为监测对象，当时间步长大于500时，速度曲线基本重叠，可近似认为时间步长大于500对计算结果精确度无影响[26]。故设置计算时间步长为1 000，收敛残差为10-6。

2 结果

2.1 流道和喷嘴的流速分布特性

图6a和图6b为直角L型流道和圆弧L型流道流场速度轮廓云图。直角L型流道内侧流场速度大，流场压力小；外侧流场速度小，流场压力大。竖直段左侧近壁面区域流场速度小，右侧流场速度大。喷嘴内部流场速度急剧增大，速度最大值在喷嘴中心轴线区域，速度由喷嘴中心轴线向两侧近壁面逐渐减小[27]。圆弧L型流道内侧流场速度大，流场压力小；外侧流场速度小，流场压力大。喷嘴内部流场速度急剧增大且呈梯度状分布，速度最大处位于喷嘴中心轴向区域，速度由喷嘴中心轴线向两侧近壁面逐渐减小。

图6 直角L型和圆弧L型流道流场速度轮廓云图Fig.6 Flow field velocity contour cloud images of right-angle L-shaped channel and Circular-arc L-shaped channel

图7是流道喷嘴截面速度分布图。两种流道喷嘴流场速度均先增大后趋于稳定。直角L型流道速度在y=13 mm达到最大值，速度最大值为156 m/s。圆弧L型流道速度在y=13.7 mm达到最大值为 178 m/s。喷嘴缩颈结构处(y=13 mm)之后，圆弧L型流道流场速度值明显大于直角L型流道流场。

图7 两种流道喷嘴截面速度分布Fig.7 Velocity distribution of nozzle sections of two flow channels

图8a和图8b是两种流道流线图。直角L型流道流线在弯曲段内、外两侧形成两处旋涡，内侧旋涡尺寸明显大于外侧，喷嘴内部流线分布较为密集。圆弧L型流道流线仅仅在弯曲段外侧出现一处旋涡，流线在喷嘴缩颈结构作用下收缩成一股集中的流线束。

图8 直角L型和圆弧L型流道流线图Fig.8 Motion pattern of right-angle L-shaped channel and Circular-arc L-shaped channel

2.2 流道和喷嘴的流场压力分布特性

图9为两种流道喷嘴截面压力分布图。

图9 两种流道喷嘴截面压力分布Fig.9 Pressure distribution of nozzle sections of two flow channels

两种流道喷嘴缩颈结构处，流场压力大幅度减小，喷嘴入口处形成了较大的压降。直角L型流道流场压力在y=13.6 mm处降低到最小值-1.95 MPa，压差为 16.95 MPa。圆弧L型流道流场压力在y=13.1 mm处下降至最低值-4.65 MPa，压差为 19.65 MPa。圆弧L型流道流场压力变化幅度大于直角L型流道流场。

2.3 流道和喷嘴的流场湍流动能分布特性

图10a和图10b为两种流道湍流动能轮廓云图。直角L型流道喷嘴入口处流场湍流动能沿喷嘴中心轴线方向呈左右两侧较均匀分布。圆弧L型流道喷嘴入口处流场湍流动能沿喷嘴中心轴线方向呈左侧小，右侧大分布。两种流道喷嘴缩颈结构处出现涡流现象，涡流区是高速射流与环境流体的强剪切作用下形成的，涡流区中心压力远远低于其他流动区域的压力，当中心压力低于饱和蒸汽压时，液体内部产生大量空泡[28]。

图10 两种流道流场湍流动能轮廓云图Fig.10 Flow field turbulent kinetic energy contour cloud images of two kinds of channels

图11为两种流道湍流动能和湍流强度分布图。在y=12 mm前，两种流道流场湍流动能未发生变化。该点之后，两种流道流场湍流动能发生剧烈变化。直角L型流道喷嘴内部流场湍流动能变化范围为875.662～1 331.24 m2/s2。圆弧L型流道喷嘴内部流场湍流动能变化范围为 519.274～812.017 m2/s2。两种流道流场湍流强度变化趋势同湍流动能类似，在y=12 mm前，两种流道流场湍流强度值均低于5%，该点之后，两种流道湍流强度急剧上升，直角L型流道流场湍流强度最大值达29%，圆弧L型流道流场湍流强度最大值达23%。

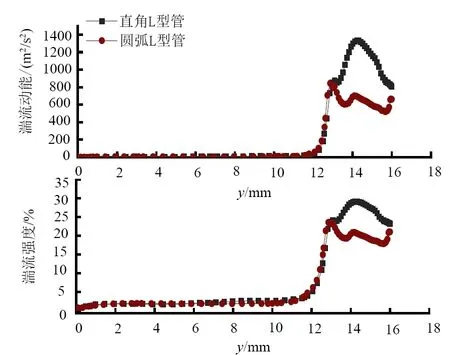
图11 两种流道y轴向近壁面湍流动能和湍流强度分布Fig.11 y-axis turbulent kinetic energy and turbulence intensity distribution near wall surface of two kinds of channels

2.4 喷嘴空化特性

两种流道气相体积分数轮廓云图如图12a和图12b所示。两种流道喷嘴内部均发生了空化现象，空化面积由喷嘴入口沿壁面延伸至喷嘴出口。直角L型流道喷嘴截面中心轴线右侧壁面出现空化区域，空化强度由轴线向近壁面逐渐增大。圆弧L型流道喷嘴截面中心轴线左右两侧均出现空化区域，空化强度由轴线向近壁面方向迅速增大。圆弧L型流道喷嘴的空化区域面积大于直角L型流道。

图12 两种流道流场气相体积分数轮廓云图Fig.12 Flow field vapor volume fraction contour cloud images of two kinds of channels

图13为两种流道气相体积分数分布图。两种流道在y=13 mm前气相体积分数为0，在该点之后，气相体积分数不断增大。说明空化效应出现在喷嘴入口处，并不断向喷嘴内部延伸至出口。直角L型流道壁面气相体积分数最大值达到0.29；圆弧L型流道壁面气相体积分数最大值达到0.53。直角L型流道最大气相体积分数占比圆弧L型流道最大气相体积分数约为45.3%。

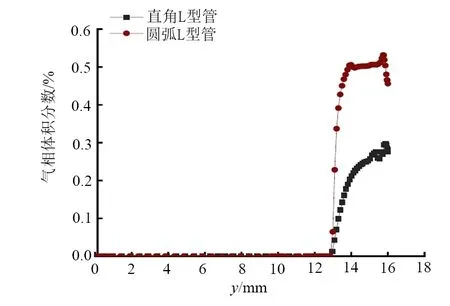
图13 两种流道y轴向近壁面气相体积分数分布Fig.13 y-axis vapor volume fraction distribution near wall surface of two kinds of channels

3 讨论

3.1 流道结构对喷嘴流速影响分析

流体流经直角L型流道弯曲段，因受离心力和惯性力作用，出现流动的分离和再附现象，形成两处旋涡区，同时产生二次流现象，二次流和主流运动方向正交，使流体质点做螺旋运动，从而引起压力降和局部水头损失，降低了能量的转换效率，动能减少，与马金英[29]关于弯管中流道流场的数值分析结果相印证。圆弧L型流道弯曲段相对直角L型流道较为平缓，流线分布均匀，仅在流道弯曲段外侧出现一处小范围旋涡，表明圆弧L型流道流场较直角L型流道局部水头损失少，转换动能多。圆弧L型流道喷嘴出口形成射流速度较高，产生的射流打击力强度较高。

3.2 流道结构对喷嘴压力影响分析

流场压力在流道喷嘴缩颈结构处迅速减小，压力势能转化为动能，速度不断增大。喷嘴空化强度与压降因素有关，压降越大，空化率越高[30]。当压力值下降至低于环境饱和蒸气压时，液体断裂产生大量气核，气核在液体中膨胀成空泡，大量空泡不断聚集形成空泡群。当外界压力增大，空泡在外界压力作用下产生溃灭机制，空泡群大量溃灭形成巨大的冲击能量。圆弧L型流道比直角L型流道流场压力下降幅度较大，形成了较大的压差，为喷嘴产生空化提供了有利的条件。

3.3 流道结构对喷嘴湍流动能影响分析

两种流道喷嘴缩颈结构处，因阻流截面造成流体运动方向改变，形成涡流区。由于在涡流区域内，质点涡旋运动消耗能量，涡旋运动的质点不断向下游移动，在一定范围内加剧了下游流体的湍流强度，使得流场的湍流动能和湍流强度迅速增大[31]。高速射流在强紊流环境下受到强剪切作用和附壁效应，液体内部发生断裂产生空泡[32]。圆弧L型流道流场比直角L型流道流场湍流动能减少 39%～40.7%，湍流强度减少20.7%，说明圆弧L型流道喷嘴流场紊流脉动幅度比直角L型流道喷嘴流场紊流脉动幅度小，造成的能量损失少[33]。

3.4 流道结构对喷嘴空化特性影响分析

液体在恒定温度下，当压力逐渐减小到饱和蒸气压以下时，液体内部会产生大量空泡，通过降低压力使液体破裂形成空泡的过程称为空化现象。液体中还含有不溶解的气核或微气泡，在压力降低的情况下，可能会生长并形成空腔，在低压空化区域会发生非常剧烈的密度变化[34-35]。空化现象发生在流道喷嘴近壁面区域，喷嘴缩颈结构致使流体发生扰动，流体速度不断增大，压力不断减小，当局部流体压力Pi小于该环境下流体的饱和蒸汽压Pv时,液体内部产生大量气泡，气泡受到高压后溃灭，形成瞬时高温高压的强烈冲击力作用在附着物表面，使附着物脱离网衣[36]。直角L型流道喷嘴近壁面仅右侧发生空化效应；圆弧L型流道喷嘴近壁面左右两侧均发生空化效应，说明高压流体在圆弧L型流道喷嘴内部可产生完整的空化环，空泡迅速向外扩散形成环状空化群。圆弧L型流道喷嘴空化区域面积和气相体积分数更大，表明圆弧L型流道喷嘴空化程度更高。圆弧L型流道弯曲段平缓，喷嘴流速高，压差变化大，空化程度高，产生了更强的射流打击力，可提高网衣清洗效率，因此圆弧L型流道作为空化射流网衣清洗装备的流道结构，更符合实际清洗工作需求。

4 结论

采用流体分析软件仿真模拟了直角L型和圆弧L型流道下喷嘴的流场分布，分析了两种流道对喷嘴流体压强分布、速度分布、湍流动能及空化程度的影响，进一步验证了圆弧L型流道为分流转盘流道优化结构，为网衣清洗装备实际加工提供参考。流体在直角L型流道形成两处旋涡，在喷嘴出口处达到最大速度156 m/s；流体在圆弧L型流道形成一处旋涡，在喷嘴出口处达到最大速度178 m/s。直角L型流道流场压降为16.95 MPa；圆弧L型流道流场压降为19.65 MPa。圆弧L型流道流场比直角L型流道流场湍流动能减少 39%～40.7%，湍流强度减少 20.7%。两种流道结构下的喷嘴均不同程度地发生了空化，直角L型流道最大气相体积分数占比圆弧L型流道最大气相体积分数约45.3%，圆弧L型流道结构喷嘴的空化区域远大于直角L型流道结构喷嘴。相比直角L型流道，圆弧L型流道喷嘴射流速度更大、能量损失更少、空化程度更高，有利于提升网衣清洗装备的清洗效率，圆弧L型流道更适用于作为网衣清洗装备分流转盘内部流道优化结构。

□