海洋柔性管缆防弯器连接结构的几何参数优化

石鸿毅，陈金龙，岳前进，陈琰霏，卢青针

(大连理工大学 a.海洋科学与技术学院；b.盘锦产业技术研究院，辽宁 盘锦 124221)

0 引 言

防弯器在海洋工程领域有着广泛应用[1]，在位的柔性管缆需要维持一定的线型[2-4]，在其过度弯曲段安装防弯器可有效补偿柔性管缆局部弯曲刚度并维持线型[5-6]。防弯器通常是一种类似于锥体的结构，由于需要与海上平台或风机桩体进行连接[7]，防弯器通常都有一个金属连接结构嵌入聚氨酯弹性体主体结构中，以实现防弯器与外部结构的固定连接。

目前，针对海洋管缆防弯器的研究大多聚焦于防弯器主体部分的分析。主体部分材料聚氨酯弹性体的本构关系对防弯器弯曲刚度影响较大[8]，考虑材料本构非线性[9-10]相较于线弹性简化模型[11-14]会使防弯器主体结构的设计更精确。前人针对防弯器的几何参数与材料研究相对成熟，但在进行有限元分析的过程中，往往忽略和简化防弯器的连接结构。在工程应用中，连接结构的设计通常以经验设计为主，未对其进行深入研究。防弯器连接结构失效发生的原因之一就是没有对连接结构进行充分分析，几何参数设计不够保守。防弯器的连接结构较为复杂，除了连接结构嵌入深度的影响[15]外，其他几何参数也对防弯器整体结构应力和海缆曲率产生一定影响，需要对各几何参数进行系统分析。

为建立对防弯器连接结构进行系统分析的方法，以柔性海缆为例，在建立包含连接结构的防弯器-海缆耦合数值模型的基础上，重点对一种常见的防弯器连接结构的几何参数进行正交试验分析，研究连接结构几何参数对海缆曲率和防弯器应力的影响，以建立对连接结构进行有效分析的方法，获得连接结构5个几何参数的变化对防弯器主要性能指标的影响规律。

1 考虑连接结构的防弯器-海缆耦合数值模型

将防弯器整体结构分为由聚氨酯弹性体制成的主体结构和由金属材料制成的连接结构两个部分。建立的耦合数值模型包括主体结构、连接结构和有防弯器作用的局部海缆(长度为5 m)，如图1所示。

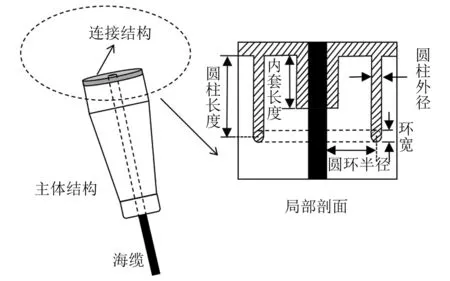
图1 防弯器整体结构与海缆的耦合模型

为对耦合模型进行计算，根据某工程项目，选择海缆直径为45 mm的4段式防弯器，其主体结构的几何参数如图2和表1所示。

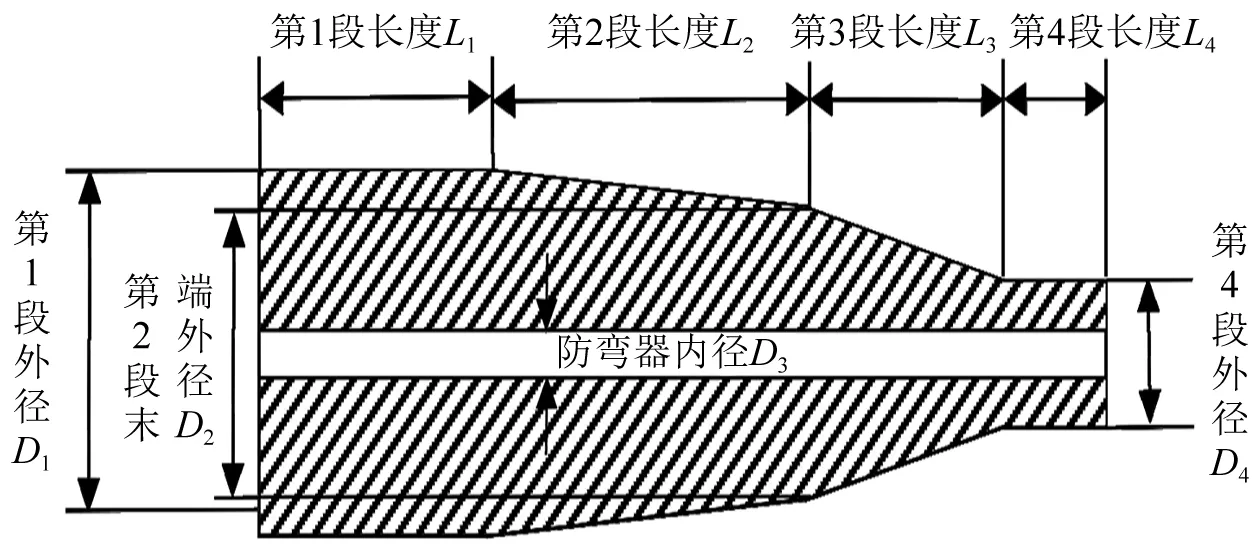
图2 防弯器几何参数示例

表1 防弯器几何参数 mm

连接结构选用工程中常用的结构形式，该形式的连接结构主要几何参数分别为圆柱长度l1、内套长度l2、环宽d1、圆柱外径d2、圆环半径r，如图3所示。

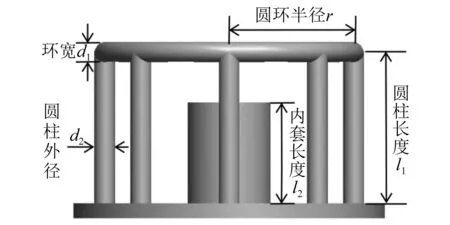
图3 连接结构主要几何参数

在对防弯器进行设计分析时，通常选择防弯器下端海缆的极限张力和张力角度[16]作为载荷(见图4)，分析极限载荷下防弯器对海缆的保护效果。

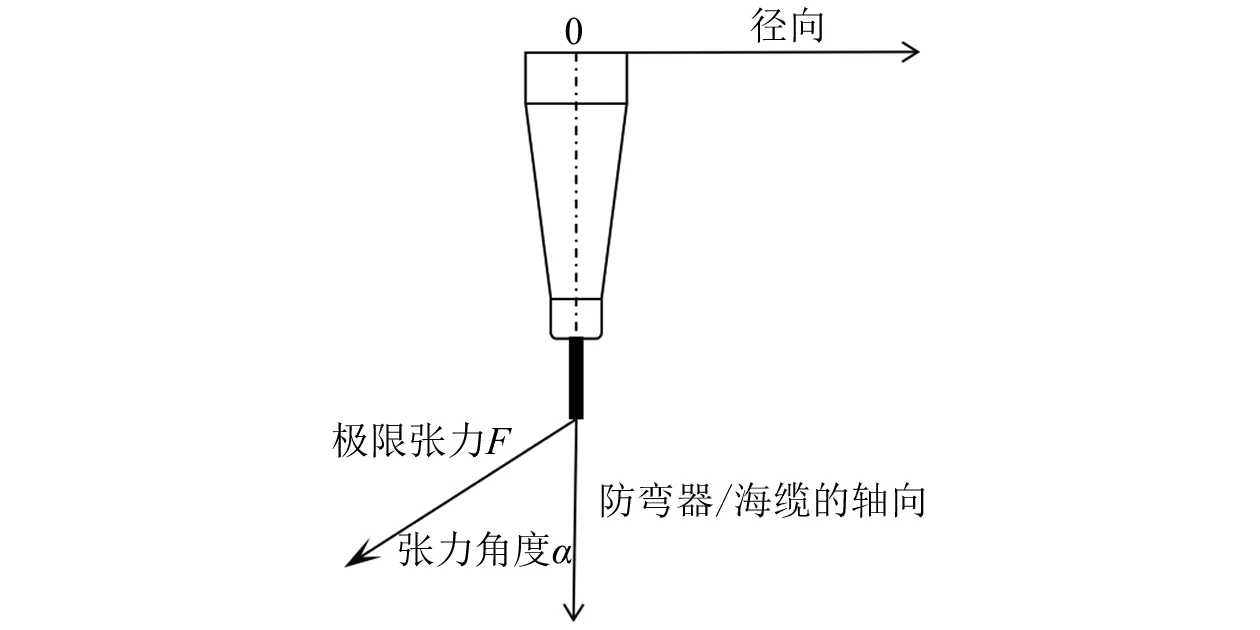
图4 海缆端部极限张力与张力角度

为获得聚氨酯弹性体的力学性能，参考《硫化橡胶或热塑性橡胶拉伸应力应变性能的测定GB/T 528—2009》[17]浇注拉伸试样并进行拉伸测试，浇注制备出的试样在拉伸过程对应的应力-应变关系如图5所示，曲线有明显的非线性特点。将应力-应变关系导入有限元模型。

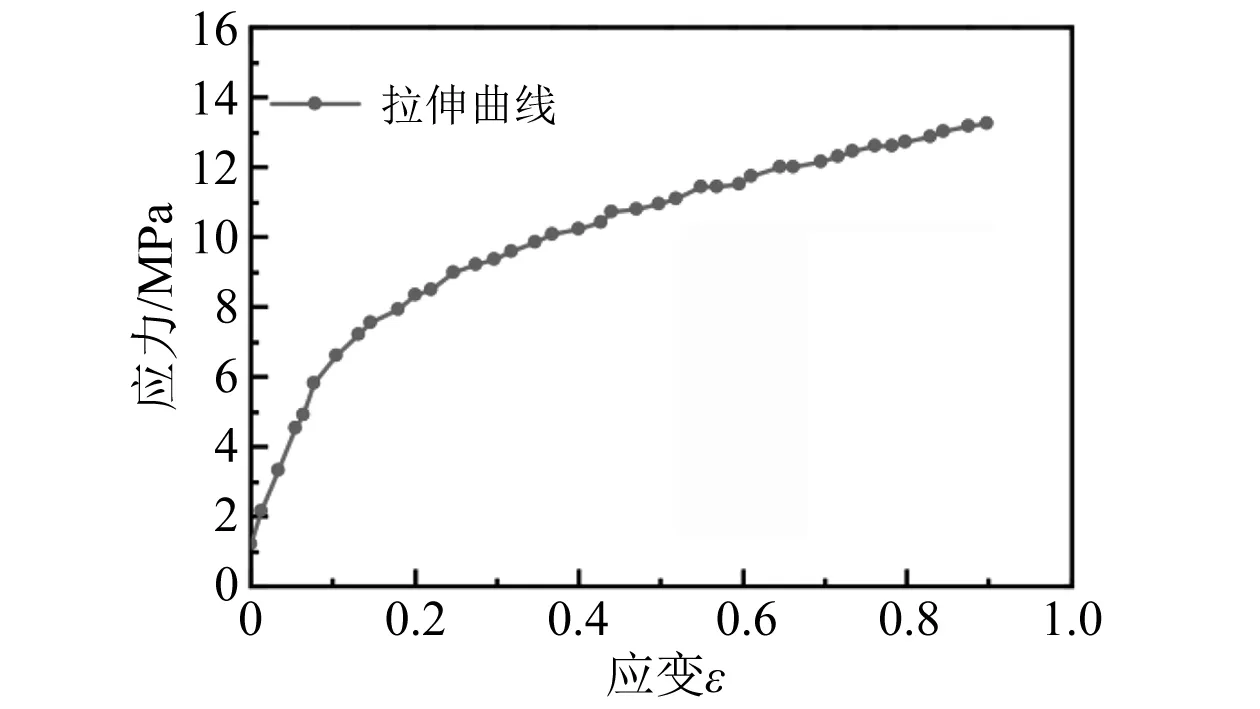
图5 聚氨酯材料应力-应变曲线

连接结构材料选择316L不锈钢，弹性模量为206 GPa，泊松比为0.3，屈服强度取352.97 MPa，极限强度取663.36 MPa[18]，采用线性-强化本构模型。海缆弹性模量等效为1 987 MPa，泊松比为0.3。

分别对导入Abaqus中的聚氨酯弹性体主体结构、连接结构和海缆赋予网格属性，由于聚氨酯弹性体具有橡胶类材料所共有的近似不可压缩特性[19]，因此聚氨酯弹性体采用杂交单元。连接结构与海缆采用非协调单元。

定义海缆与连接结构、海缆与聚氨酯弹性体之间的接触：切向行为选择“罚”公式，摩擦因数为0.3；法向行为选择“硬”接触。聚氨酯弹性体与连接结构的接触为法向“硬”接触。

为验证该数值模型的有效性，设计张力为1 100 N，张力角度为90°的等比例试验。通过简易的测试方法，获得该张力下防弯器的实际径向位移，与数值模型结果的对比如图6所示。由图6可知，防弯器数值结果与试验结果基本一致，表明数值结果对防弯器实际变形的描述是准确的。

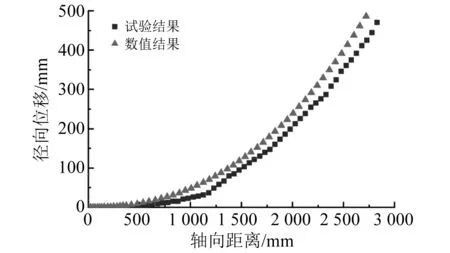
图6 数值结果与试验结果对比

2 基于耦合模型的连接结构的几何参数分析

2.1 正交试验设计

为探究连接结构几何参数对整体耦合结构的影响，对图3所示连接结构的5个几何参数进行正交试验设计。

对这5个几何参数分别取4个水平，因素水平如表2所示，选择L16(45)正交表(见表3)进行试验。基于表3，建立16个耦合模型。施加于海缆的张力均为8 000 N，张力角为60°。将张力分解为轴向张力分量(6 928 N)和径向张力分量(4 000 N)，输入有限元模型中。

表2 连接结构几何参数因素水平 mm

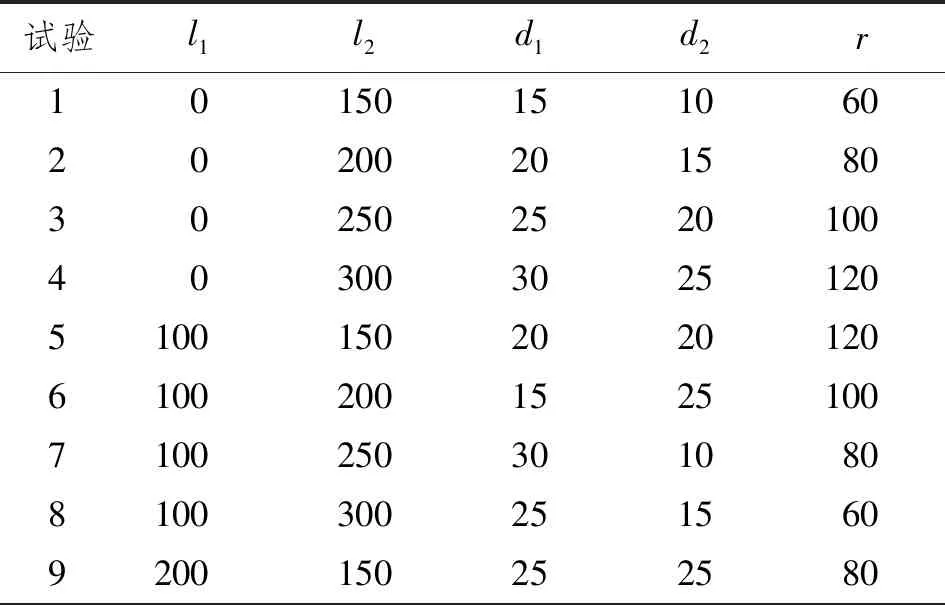
表3 L16(45)正交表 mm

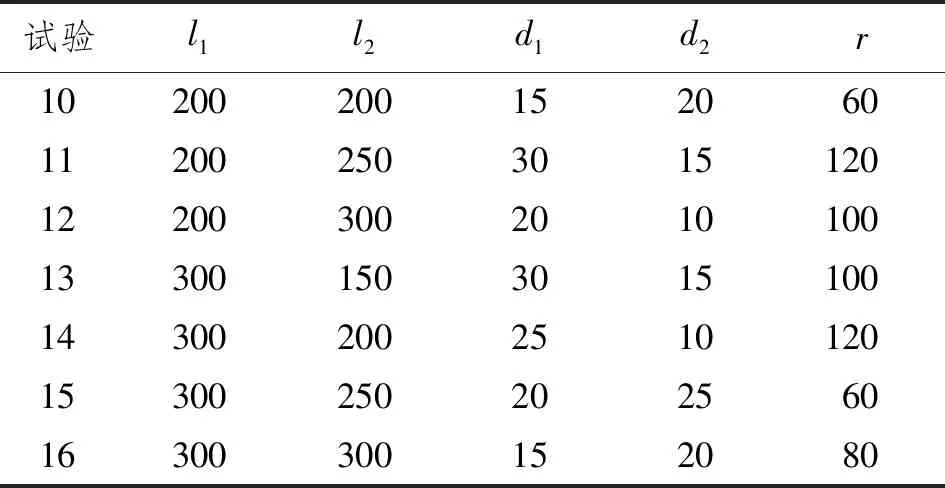
续表3 L16(45)正交表 mm

2.2 数值结果分析

检验防弯器对海缆的保护效果的重要指标之一为海缆受载荷作用下的最小弯曲半径，海缆在服役期间的弯曲半径不得小于其最小弯曲半径，否则会发生破坏。与最小弯曲半径对应的是海缆的最大曲率。除此之外，防弯器主体结构和连接结构的最大Mises应力也需要加以考虑，进而保证满足强度要求(本文重点在于分析应力最大值随连接结构几何参数的变化规律，暂不考虑强度破坏)。

分别提取各组耦合模型中的海缆最大曲率，以及主体结构和连接结构的最大Mises应力。

2.2.1 海缆最大曲率

海缆弯曲半径与曲率的对应关系为

(1)

式中：ρ为海缆曲率；R为海缆弯曲半径。海缆因其极大的长细比，可简化为梁模型，应用平断面假设可得到海缆应变与曲率的关系为

(2)

式中：ε为海缆应变；d为海缆直径。提取海缆上各点的应变，按式(2)进行处理，得到海缆曲率分布如图7所示(海缆的轴向和坐标原点如图4所示)。

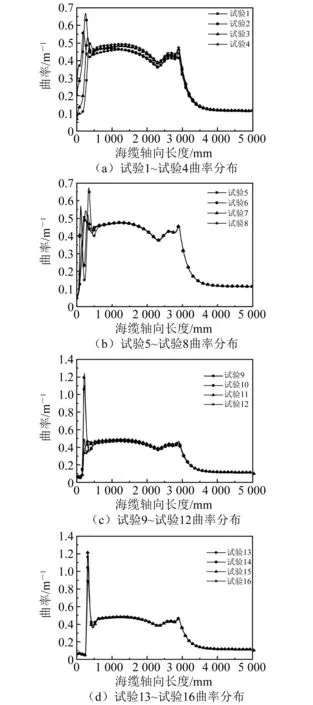
图7 海缆曲率分布

由海缆曲率分布结果可知，改变连接结构的几何参数影响海缆0～500 mm段曲率分布，且连接结构对0～500 mm段的海缆曲率峰值影响较大。

分别提取16组正交试验中的海缆最大曲率，计算各几何参数的极差R：

(3)

(4)

式(3)和式(4)中：ki为试验结果的平均值；Ki为i水平对应的试验结果之和；i=1,2,3,4；s为同一列中i水平出现的次数。各试验因素极差如表4所示。

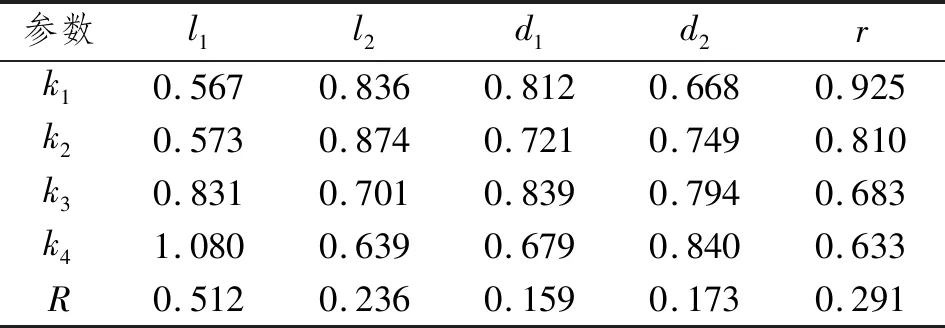
表4 海缆最大曲率极差 m-1

比较各因素的极差大小，可看出各几何参数对海缆最大曲率的影响主次水平依次为l1>r>l2>d2>d1，l1对海缆最大曲率的影响占主导作用。为反映各因素水平对曲率极值影响的趋势，取每个水平的最大曲率的均值为纵轴，水平为横轴，形成如图8所示的趋势图。

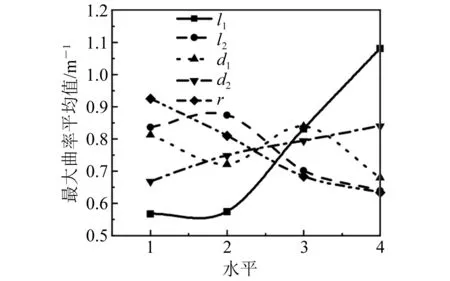
图8 各因素对最大曲率影响趋势

在海缆最小弯曲半径的制约下，设计防弯器时需尽可能保证海缆的曲率平滑过渡。海缆最大曲率在一定范围内越小，防弯器的设计就越优。由图8可知，为获得海缆最大曲率的极小值，0～100 mm为主导因素l1的优设计区间。对于非主导因素，r≥120 mm为优设计区间，l2≥300 mm为优设计区间，0～10 mm为d2的优设计区间，d1≥30 mm为优设计区间。在进行连接结构的设计时可在因素影响水平主次顺序的条件下，在各参数的优设计区间进行设计。

2.2.2 连接结构最大Mises应力

在考虑海缆曲率分布的前提下，还需对防弯器连接结构的应力进行分析，确保连接结构强度满足要求。提取16个模型中连接结构的Mises应力的最大值，根据式(3)和式(4)计算各几何参数的极差，如表5所示。

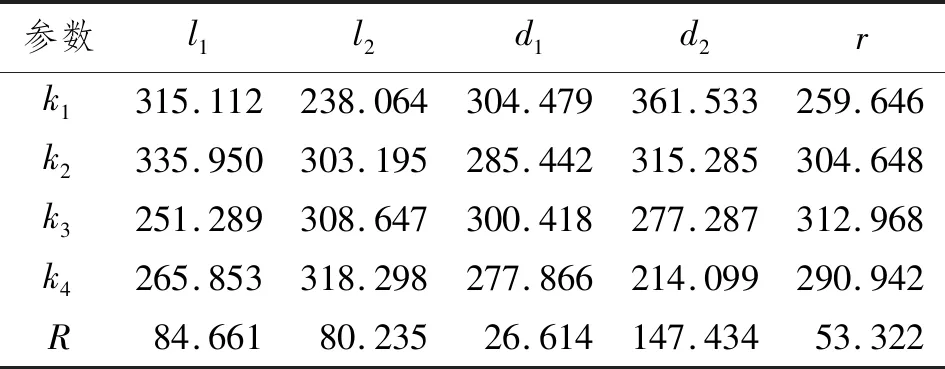
表5 连接结构最大Mises应力极差 MPa

比较各因素的极差大小，可看出各几何参数对连接结构最大Mises应力影响的主次水平依次为d2>l1>l2>r>d1，d2对连接结构最大Mises应力的影响占主导作用。为反映各因素水平对连接结构最大Mises应力影响的趋势，取每个水平的最大Mises应力的平均值为纵轴，水平为横轴，形成如图9所示的趋势图。

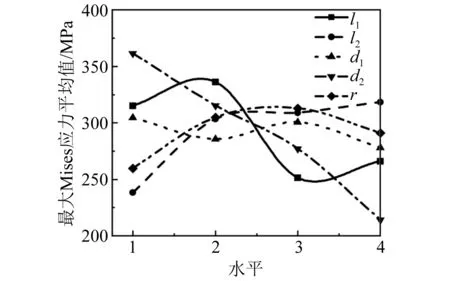
图9 各因素对连接结构最大Mises应力影响趋势

在对防弯器进行设计时，希望整体结构在满足工程需要的前提下，整个结构的最大Mises应力尽可能降至最小。由图9可知，对于连接结构的最大Mises应力，d2≥25 mm为主导因素d2的优水平区间，200～300 mm为l1的优设计区间，0～150 mm为l2的优设计区间，r≥120 mm和r≤60 mm为r的优设计区间，d1≥30 mm为优设计区间。

2.2.3 主体结构最大Mises应力

类似地，从计算结果中提取主体结构的最大Mises应力，根据式(3)和式(4)计算各几何参数的极差，如表6所示。

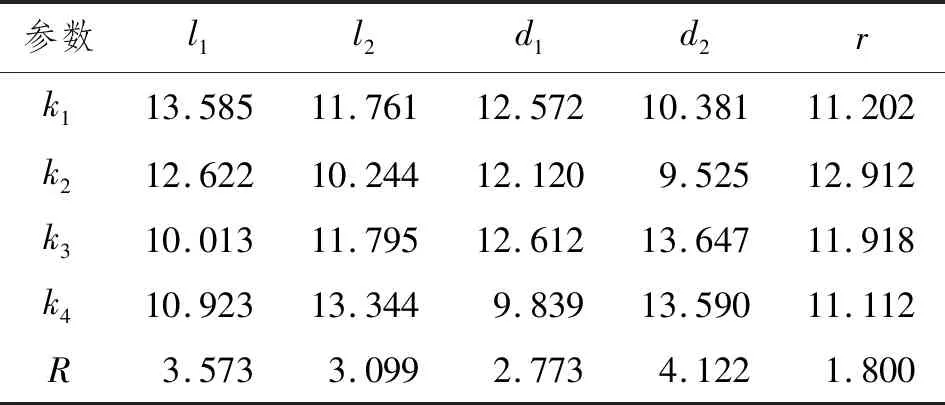
表6 主体结构最大Mises应力极差 MPa

比较各因素极差的大小，从表6可看出各几何参数对主体结构最大Mises应力影响的主次水平依次为d2>l1>l2>d1>r，d2对主体结构最大Mises应力的影响占主导作用。为反映各因素水平对主体结构最大Mises应力影响的趋势，形成如图10所示的趋势图。

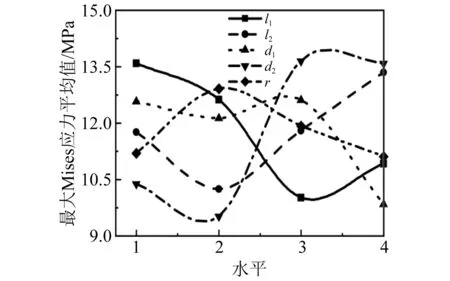
图10 各因素对主体结构最大Mises应力影响趋势

在一定范围内，主体结构的最大Mises应力越小，防弯器的设计越合理。由图10可知，对于主体结构的最大Mises应力，10～15 mm为主导因素d2的优设计区间，200～300 mm为l1的优设计区间，150～250 mm为l2的优设计区间，d1≥30 mm为优设计区间，r≥120 mm和r≤60 mm为r的优设计区间。

3 结 论

防弯器连接结构缺乏有效的设计校核方法，所提出的耦合模型和正交试验法能以较高的效率进行连接结构的设计与校核，主要结论如下：

(1)包含连接结构的防弯器-海缆耦合数值模型与测试结果吻合度较高，该耦合模型可用于防弯器连接结构的设计校核。

(2)基于正交试验方法，能以较高效率获得连接结构几何参数的优设计区间及对试验指标影响的主次顺序。

(3)在设计防弯器连接结构时需要对内套长度和圆柱外径进行主要分析。内套长度l1对海缆曲率影响显著，在设计区间内，l1的设计值不宜过大，超出一定范围，l1的值越大，海缆曲率越大。圆柱外径d2对防弯器结构的应力影响显著，d2的值越大，连接结构的最大Mises应力越小，但是d2的设计值并非越大越优，需结合主体结构最大Mises应力对应的d2优设计区间进行综合考量。