含摩擦摆高位连体结构抗震性能数值分析研究*
缪志伟, 马栋梁, 张志强, 李新舫
(1 东南大学混凝土及预应力混凝土结构教育部重点实验室,南京 211189;2 武汉开来建筑设计股份有限公司,武汉 430061)
0 概述
随着社会经济的发展和建筑结构技术的不断提高,高位连体结构在建筑工程中应用越来越广泛。高位连体结构在造型外观、连接方式和结构设计与分析等方面呈现出了相当的复杂性和超限性[1]。目前各国专家学者对高位连体结构的研究主要体现在其支座布置形式、结构动力特性、抗震性能及安全评估等方面。
在此类结构中,连接体与主体塔楼的连接形式是结构设计与分析的重点。弱连接作为连体结构常用的连接方案,支座部位往往需要设置成一端或者两端弱连接的形式,以释放地震作用下连接体较大的内力响应,弱连接下的支座位移及支座反力分析与设计是高位连体结构设计的关键问题之一[2]。摩擦摆系统/支座(Friction Pendulum System/Bearing,简称FPS/FPB)由于对地震激励频率范围内的低敏感性和高稳定性,并具有较强的限位、自复位性能和优良的隔震与耗能特性等优点,早已经在工程加固和桥梁隔震中得到了广泛应用[3]。本文基于合理的结构数值分析模型,针对设置摩擦摆支座的弱连接方案下的某高位连体结构进行了罕遇地震作用下的弹塑性时程分析,并且对比了设置铰支座的强连接方案,分析了两种不同连接方案的抗震性能,为工程设计提供参考。
1 工程概况
1.1 基本信息
该工程为位于湖北省武汉市某商业地块的两栋对称塔楼组成的连体高层结构,塔楼地下1层,地上22层,主体塔楼建筑高度102.3m。地下室层高5.2m,1层层高6.0m,2层层高5.2m,3层层高6.0m,4~20层为标准层,层高均为4.5m,21和22层层高分别为3m和5.6m,23层框架层层高为4.4m。根据建筑方案,本工程在两栋塔楼的顶部(标高106.7m)正中间处布置一个钢结构棚架。该棚架采用管桁架,建筑高度为3.6m,平面呈弧形,内弧跨度为49.2m,外弧跨度为58.1m,棚架平立面尺寸、主要构件截面尺寸以及弱连接方案支座布置如图1所示,两边各有36m长度的部分为塔楼支承区域。因此,两个塔楼通过顶部钢棚架形成了高位连体结构,而设置于两塔楼主体结构和钢棚架之间的23层框架则是连体体系的关键连接受力部位,如图2所示。
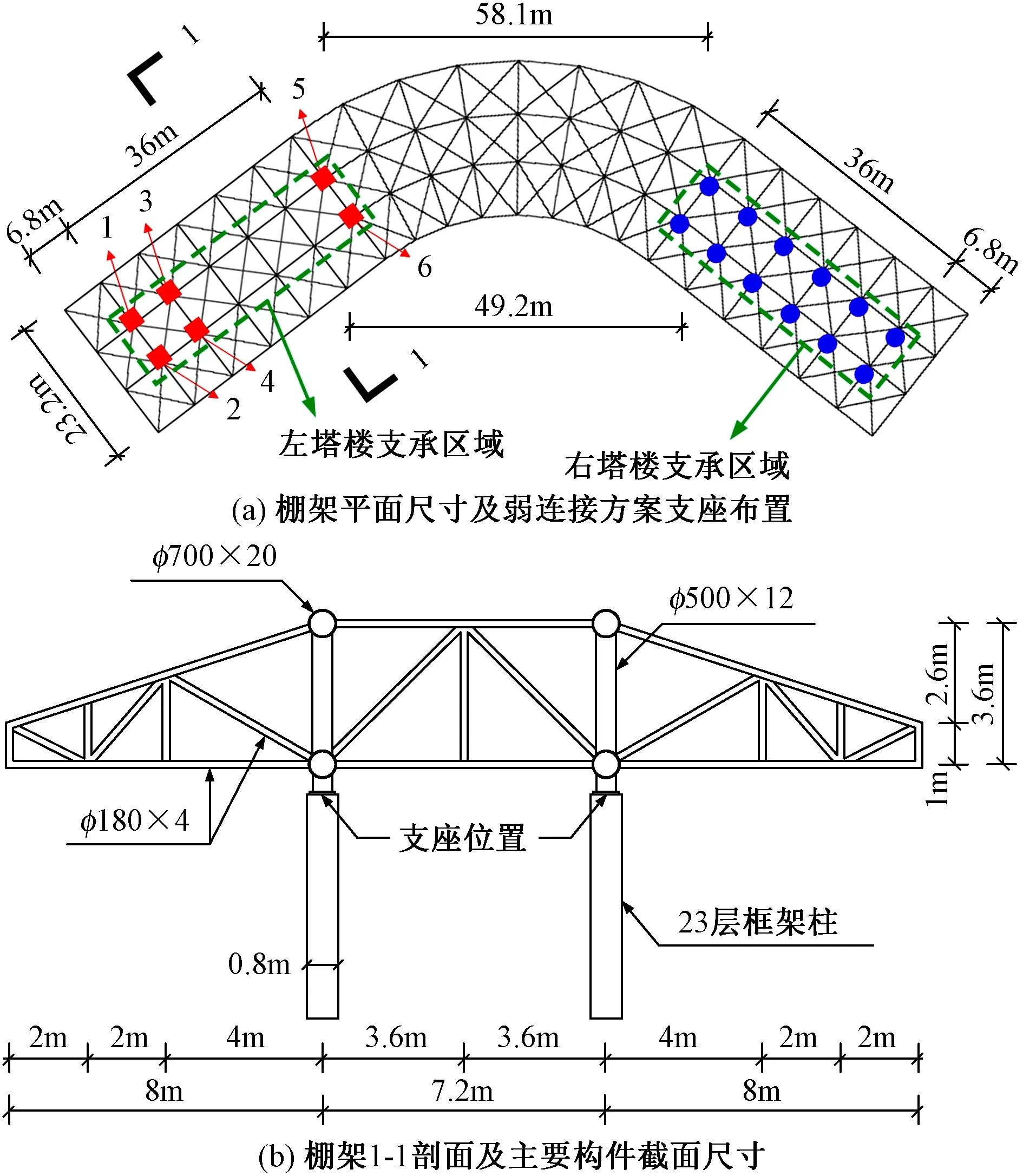
图1 钢结构棚架尺寸及弱连接方案支座布置

图2 整体结构分析模型
拟建场地位于抗震设防烈度6度区,设计基本地震加速度为0.05g,设计地震分组为第一组,建筑场地类别为Ⅱ类,场地特征周期值为0.35s。本工程两栋塔楼采用RC框架-剪力墙结构体系,顶部棚架采用钢结构管桁架。塔楼4层楼面以下框架和剪力墙的抗震等级为二级,4层楼面以上为三级。考虑屋顶钢棚架对下部结构的影响,钢棚架下部1层框架抗震等级为二级。根据相关规范[4-5],该工程高度未超限,也不存在其他不规则项。
1.2 连体连接方案设计
在高位连体结构的设计中,连体与两侧塔楼的连接方案,通常会采用一端或者两端弱连接的形式,以便在地震作用下释放较多内力,避免连接处应力集中产生严重损伤破坏。但另一方面,弱连接方案可能导致连接部位产生较大的相对位移,需要进行进一步校核。
对于本工程,由于钢棚架是通过若干支座固定在主体塔楼顶部的23层框架柱顶端上,因此对此处的连接支座考虑了两种方案。方案一是在每个塔楼23层框架柱顶均设置12个铰支座来支承钢棚架,共计2×12个铰接支座。图1(a)所示的由右塔楼支承的钢棚架区域内的12个圆形标记点即为右塔楼23层框架柱的铰支座位置,左塔楼顶部的12个支座位置与右塔楼支座对称。方案二则在保留方案一右塔楼顶12个铰接支座的同时,在左塔楼框架柱顶设置若干摩擦摆支座,使地震作用下左塔楼和棚架之间可以适当相对滑动。显然,方案一中的钢棚架对于两个塔楼的联系作用更强,本文称方案一为强连接方案,方案二为弱连接方案,从而对这两种不同连接方案下整体结构的抗震性能和连接部位的损伤情况进行对比分析。
需要说明的是,在方案二中,为了避免摩擦摆支座在重力作用下产生竖向拉力,通过先期试算确定了左塔楼顶部设置6个摩擦摆支座,如图1(a)所示。图1(a)中左塔楼1~6号支座即为摩擦摆支座。方案一和方案二中右塔楼顶12个铰接支座的布置形式完全一致。
2 有限元模型简介
2.1 结构有限元分析模型
在MSC.MARC软件中建立此结构双塔弹塑性分析模型,整体结构模型如图2所示。本工程结构弹塑性分析中,采用文献[6-7]所开发的纤维梁模型来模拟RC框架构件(框架梁、框架柱),纤维梁单元以MSC.MARC中的98号梁单元(铁木辛柯梁)为基础,并通过MSC.MARC提供的UBEAM用户子程序接口嵌入相关程序实现。混凝土和钢筋材料单轴加载的本构关系详见文献[6]。其中,混凝土本构关系可以合理反映受压混凝土的约束效应(箍筋约束混凝土采用Mander约束混凝土本构关系;非约束混凝土采用《混凝土结构设计规范》(GB 50010—2010)[8]建议的混凝土本构),以及循环往复荷载下的滞回行为(包括刚度和强度退化)和受拉混凝土的“受拉刚化效应”;钢筋本构关系则可以在再加载路径上合理考虑钢筋材料的Bauschinger效应。关于纤维梁模型有效性的验证可参阅文献[6-7]。
采用文献[7,9]提出的弹塑性分层壳单元模拟RC剪力墙(包括跨高比较小的连梁),弹塑性分层壳单元基于MSC.MARC所提供的75号厚壳单元。对于剪力墙中的竖向和水平分布筋,选用“弥散”钢筋建模方式;对于剪力墙边缘构件、连梁等特殊配筋部位,采用“离散”钢筋建模方式,即利用MSC.MARC的“INSERTS”功能,就能够使杆单元模拟的钢筋和壳单元模拟的混凝土之间位移协调并共同工作。在分层壳墙模型中,出于计算量和精度的综合考虑,本项目主要采用MSC.MARC中定义的弹塑性-断裂本构关系,其中混凝土材料受压弹塑性行为基于经典增量弹塑性本构理论,而混凝土断裂行为则采用弥散裂缝模型来描述。关于分层壳模型有效性的验证可参阅文献[7,9]。
考虑到结构中没有楼板大开洞情况,各楼层的楼板采用刚性楼板假定,在模型中约束同一楼层平面处各节点沿两个水平方向的平动自由度和绕竖直方向的转动自由度。对于弱连接方案模型,本文利用MSC.MARC的用户二次开发功能开发了特殊弹簧单元以实现模拟摩擦摆支座的各向力学行为,详见2.2节。
2.2 摩擦摆简化力学模型
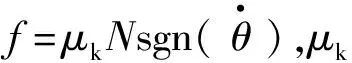
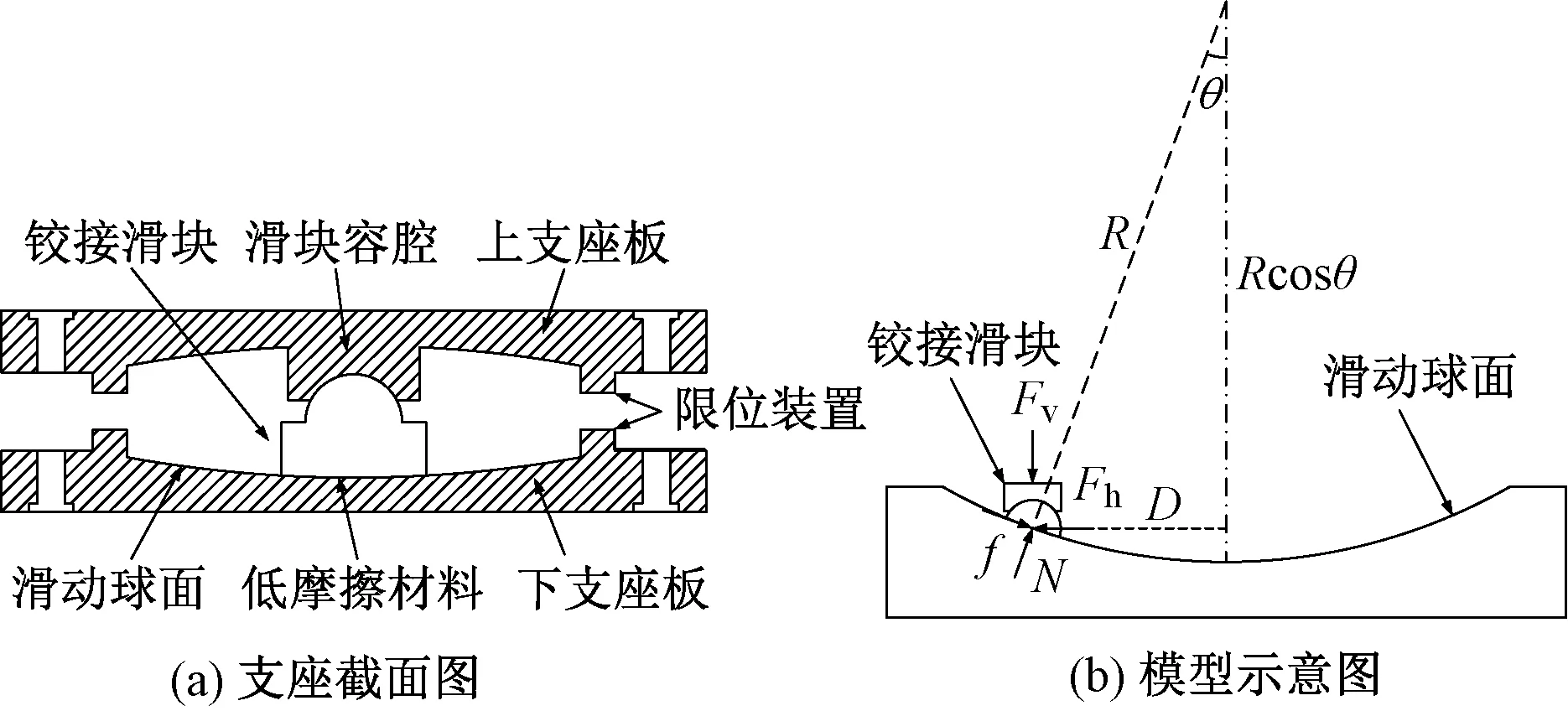
图3 摩擦摆支座截面及理论模型示意图[10]
Fv=KvR(1-cosθ)
式中Kv为摩擦摆支座的竖向受压刚度。
另外,需要说明的是,就摩擦摆支座本身而言,是不能承受竖向拉力的。然而,在罕遇烈度三向地震作用下,个别摩擦摆支座有可能出现竖向压力消失而上浮的情况,因此在工程实践中一般要设置抗拉装置,由其提供支座拉力。为了给抗拉装置的设计提供参考,依据工程经验以及常用抗拉装置的规格,本文数值模型中暂时设定当地震过程中摩擦摆支座需要承受竖向拉力时,相对应的竖向受拉刚度为受压刚度的1/10。根据摩擦摆支座的受力状态以及支座是否起滑,当滑块滑动转角θ较小时,其水平力计算公式如表1所示。

摩擦摆支座水平力计算公式 表1
在MSC.MARC有限元模型中,在相应的节点设置“弹簧连接(link-spring)”属性,并通过用户二次开发子程序USPRING编写相关程序,实现模拟摩擦摆支座的力-位移关系特性。
根据相关厂家提供的产品型号及对应的规格参数,本工程摩擦摆支座参数统一取为轴向受压刚度为2×103kN/mm,发生滑移前的初始水平刚度为4kN/mm,静摩擦系数为0.06,动摩擦系数为0.04,摩擦面曲率半径为3m,竖向压力限值为6 000kN,水平方向最大滑移量为400mm。
2.3 模态分析结果
首先对结构进行模态分析,表2为双塔结构模型强连接方案和弱连接方案对应的前三阶模态结果。分析表明,采用强连接方案后,双塔结构的各阶周期相对于弱连接方案略有减小。这是由于上部棚架增强了下部两塔楼之间的联系,提高了整体结构刚度。然而由于上部棚架本身的刚度有限,且即使是强连接方案,上部棚架与下部塔楼之间的连接采用的也是铰接支座,因此这种增强和提高作用是很有限的。
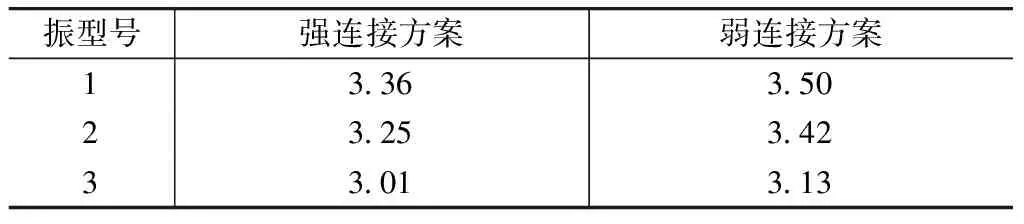
模态分析结果(前三阶模态周期)/s 表2
3 罕遇地震下的弹塑性时程分析
3.1 地震作用参数
本工程在小震动力时程分析计算时选用了5条天然波和2条人工波,且将选取的7条地震波的平均地震影响系数曲线与规范规定的振型分解反应谱法所采用的地震影响系数曲线进行了对比,表明本文所选取的地震波在统计特性上与目标反应谱较为吻合,可用于时程分析。考虑到罕遇地震下弹塑性时程分析庞大的计算工作量,本文在此前的7条地震波中选取3条波,分别是天然波1:HOLLYWOOD、天然波2:KATAKHAL、人工波:USER845,对双塔结构模型进行罕遇地震下的弹塑性时程分析。在前述摩擦摆支座力计算公式中,摩擦摆支座的竖向力会对实时的水平力数值产生影响,因此必须考虑三向地震作用,地震峰值加速度PGA设置为125gal,对应于6度(0.05g)罕遇地震的水平,两个水平向(X,Y向)和竖向(Z向)三个主轴方向按照地震动峰值为1∶0.85∶0.65进行三轴输入。根据水平地震作用施加的主、次方向不同,分为2个地震工况:1)地震工况1,水平地震动方向为单塔结构的对称轴方向;2)地震工况2,水平地震动方向为连体结构的对称轴方向。各工况的水平地震作用主方向如图4所示。
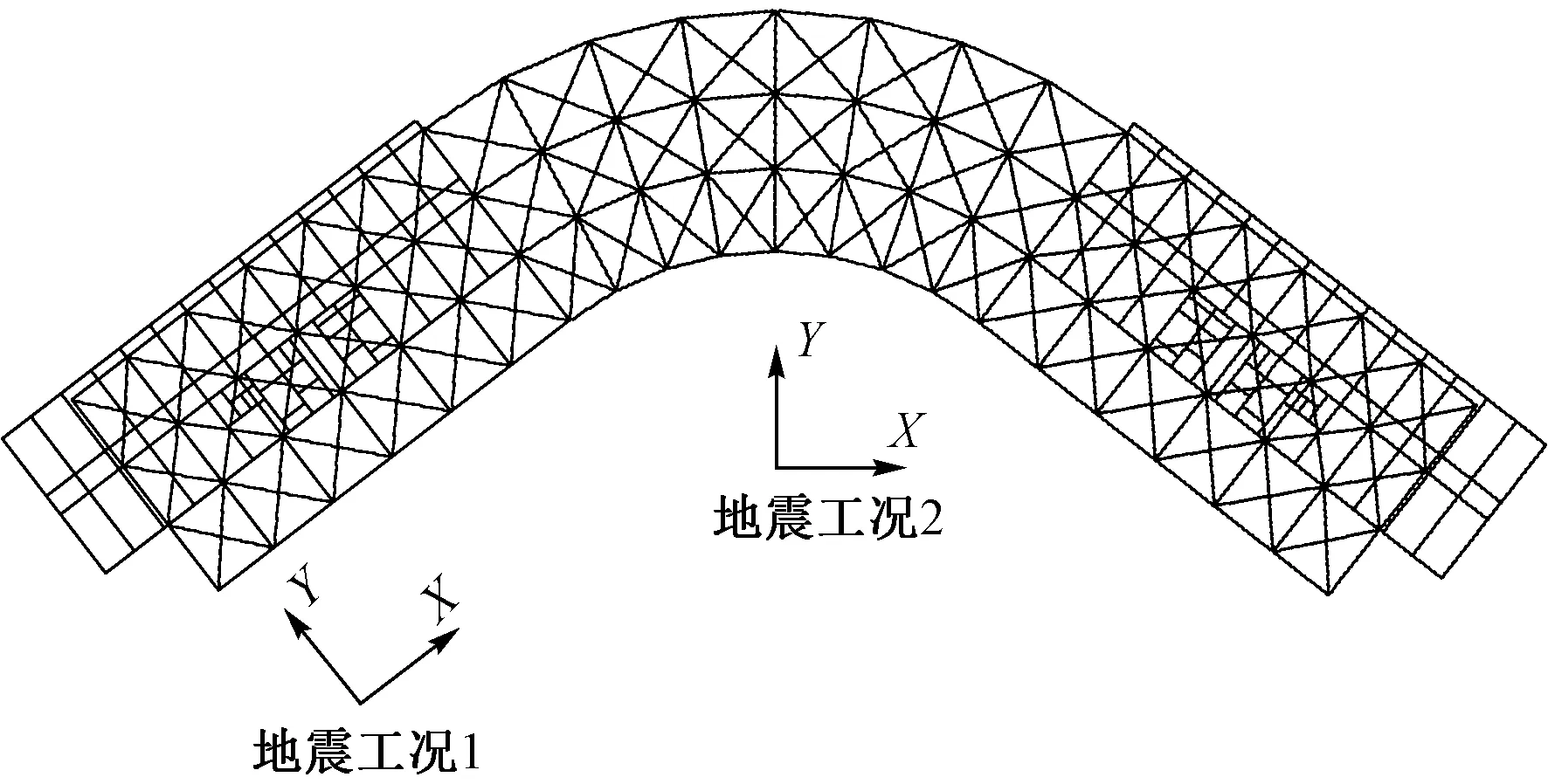
图4 考虑不同水平地震动方向的两种工况
3.2 罕遇地震下的层间位移角计算结果
统计各条波所有工况下主体塔楼结构的最大层间位移角分布,图5~6给出了X向的分布结果,表3则给出了各层结果中的层间位移角最大值θmax及相应楼层n的信息。可见,强连接方案和弱连接方案中,X向罕遇地震下结构的最大层间位移角(出现楼层)分别为1/161(12层),1/143(15层)。两种方案下的最大层间位移角结果有一定差别,但差别不大,这说明上部棚架结构和下部双塔楼之间采用不同的连接方案对下部主体塔楼的大震位移响应有一定影响,但总体上影响较小。另外,两种方案下工况2计算的最大层间位移角均大于工况1的计算结果,说明在双塔结构分析中,工况2对结构而言更不利,必须要加以考虑。参考《高层建筑混凝土结构技术规程》(JGJ 3—2010)[5],本工程设定结构抗震性能目标为D+,以1/135作为弹塑性层间位移角限值。根据图5,6可知,无论采用哪种连接方案,结构在罕遇地震作用下的X向弹塑性层间变形完全满足性能目标D+的要求。同样,Y向层间位移角的统计结果也显示结构完全满足预设性能目标要求,限于篇幅,不再赘述。
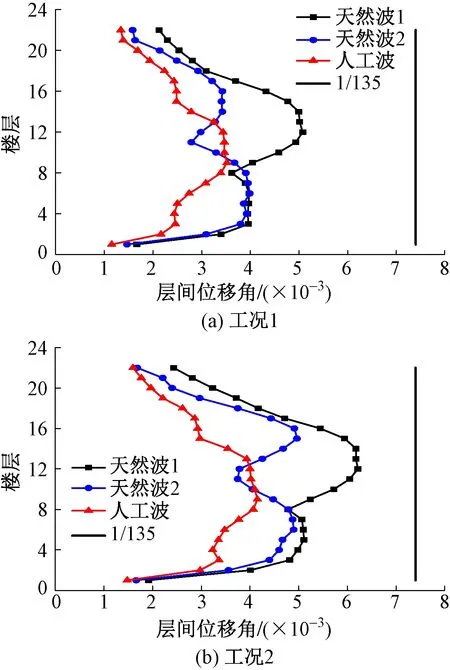
图5 强连接方案X向罕遇地震下主体结构层间位移角
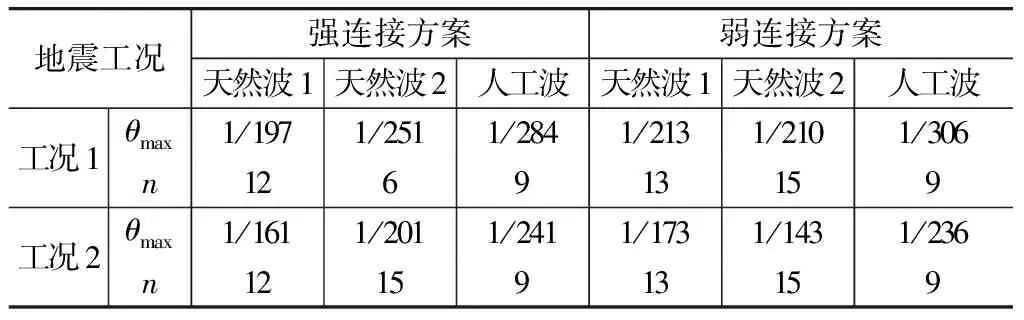
各工况作用下X向最大层间位移角及所在楼层 表3
3.3 罕遇地震下的基底总剪力计算结果
以天然波1为例,给出了两种方案不同工况下的X向基底总剪力时程结果,如图7,8所示。由图7,8可见,工况1作用下,强连接方案和弱连接方案下结构最大基底总剪力分别为23.3×103,23.2×103kN;工况2作用下,强连接方案和弱连接方案下结构最大基底总剪力分别为29.0×103,28.8×103kN。说明采用强连接方案后,双塔结构的最大基底总剪力相对于弱连接方案略有提高,这是由于上部棚架增强了下部两塔楼之间的联系,提高了整体结构刚度,故结构所受到的总地震力也有所增大,然而这种增强和提高作用是很有限的。这与前述模态分析对比的结果一致。其次,两种方案下工况2计算的最大基底总剪力均大于工况1的计算结果,说明工况2下结构的地震作用更大,对结构而言更加不利,与3.2节的计算结论相一致。
3.4 罕遇地震下的摩擦摆支座力-位移结果
对于双塔结构采用弱连接方案的模型,需要进一步考察摩擦摆支座的最大出力和滑移结果。以天然波1为例,图9和图10分别给出了双塔弱连接方案模型计算得到的工况1(水平向地震以X向输入为主)下出力相对较大的1,3,5号摩擦摆支座水平力-位移和竖向力-位移的关系曲线,各工况作用下摩擦摆支座最大位移和最大反力计算结果如表4所示。结果表明,在罕遇烈度三向地震作用下,摩擦摆支座最大水平位移约为259mm(工况1中1号支座),最大水平力为400kN(工况1中5号支座);在罕遇烈度三向地震作用下,摩擦摆支座可能会出现小幅受拉的情况。支座出现的最大竖向拉力为409kN(工况2中3号支座),而支座竖向压力最大约为4 795kN(工况2中5号支座)。以上结果表明,弱连接方案中设定的摩擦摆参数(2.2节)可以满足罕遇烈度三向地震作用下的工程设计要求。
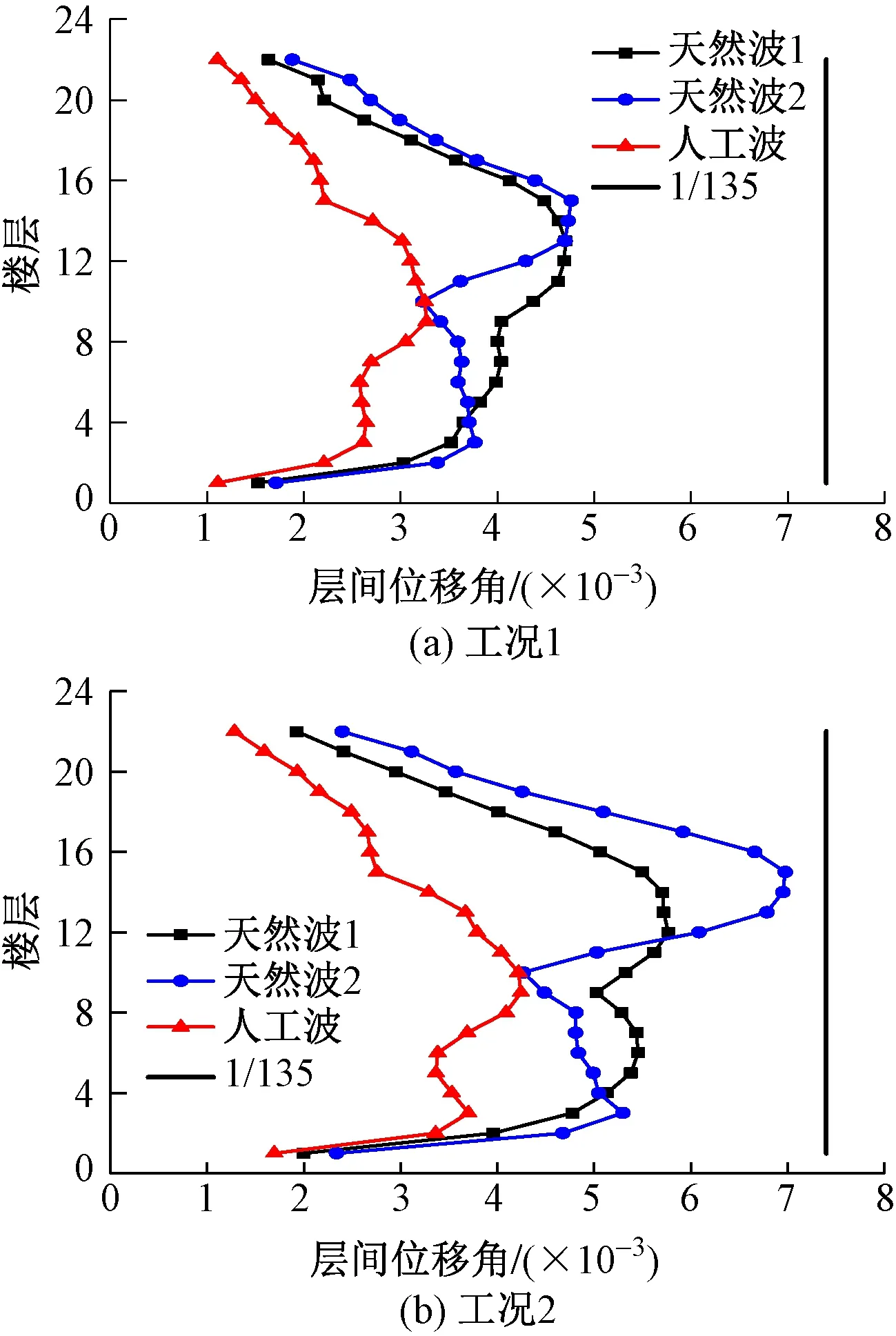
图6 弱连接方案X向罕遇地震下主体结构层间位移角
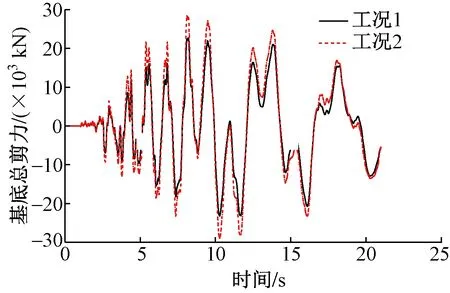
图7 强连接方案X向基底总剪力

图8 弱连接方案X向基底总剪力

图9 摩擦摆支座水平力-位移曲线
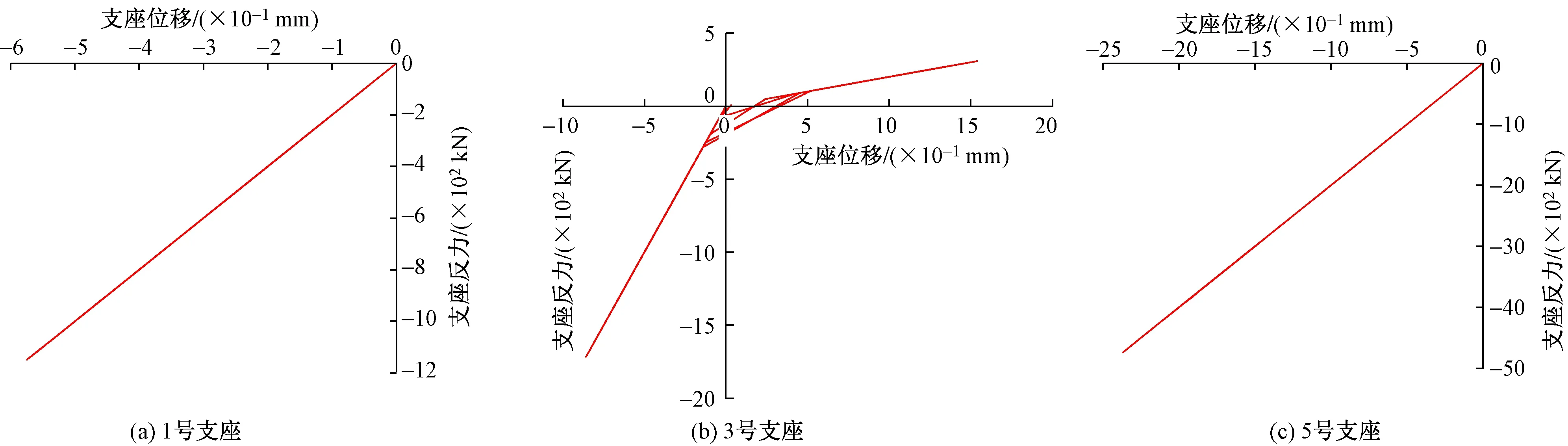
图10 摩擦摆支座竖向力-位移曲线
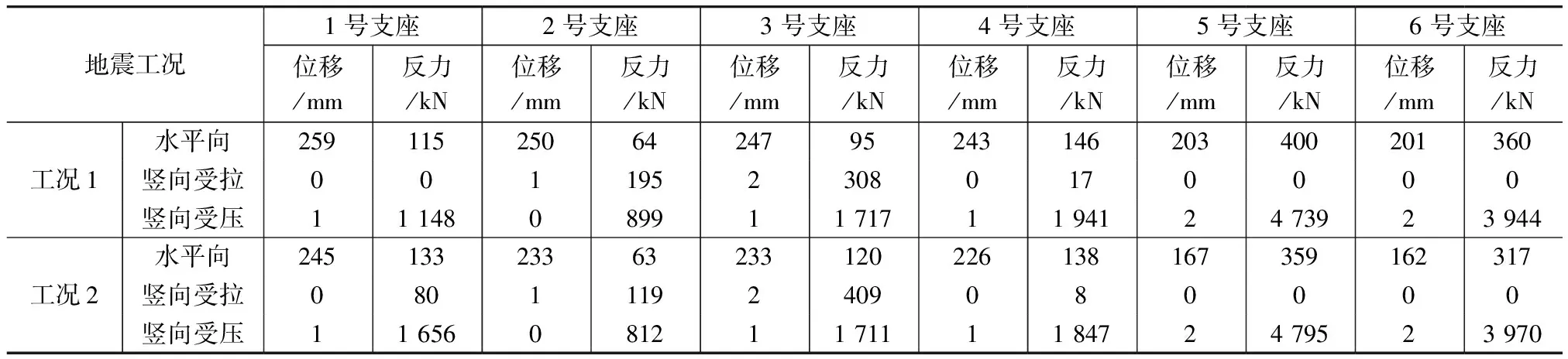
各工况作用下摩擦摆支座最大位移和最大反力对比 表4
为了考察两种方案下的结构响应差异,以天然波1为例,表5给出了工况1下两种方案1~6号支座最大水平剪力结果。可以看出,相对于强连接方案约束较强的铰接支座,弱连接方案的摩擦摆支座的水平剪力大大降低,从而可以改善连接体及连接部位的受力性能(将在4.4节进一步论述)。

不同方案下支座最大水平剪力对比/kN 表5
4 罕遇地震下的结构损伤分布与抗震性能水准评价
4.1 整体结构模型塑性铰分布
以天然波1为例,图11给出了双塔结构强连接方案在工况1(水平向地震以X向输入为主)下主体塔楼结构塑性铰分布云图结果。图中的浅色线段表示结构处于弹性状态(钢筋未屈服),而深色线段则表示结构的该部位(框架梁、框架柱、连梁、墙肢约束边缘构件)有钢筋屈服,可视为出现塑性铰。观察发现在整个地震过程中,中部楼层连梁和框架梁形成了较多的塑性铰,而作为竖向构件的墙肢和框架柱一直都没有形成塑性铰,这说明结构损伤破坏模式为“强墙肢,弱连梁”和“强柱弱梁”,各层连梁和框架梁作为结构的耗能构件有效起到了耗散地震输入能量的作用,从而保护结构中更为重要的竖向构件。弱连接方案和强连接方案各工况的结果也与上述结论相同,不再赘述。
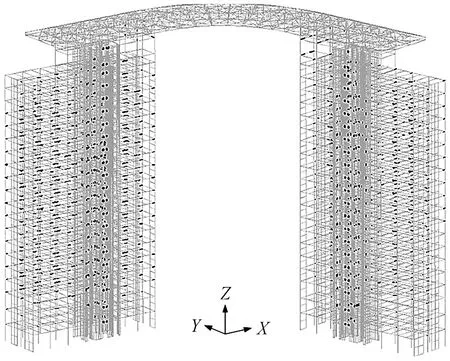
图11 强连接方案整体结构塑性铰分布云图
4.2 结构构件损伤性能水准指标定义
根据以上的弹塑性分析建模单元描述可知,无论是框架构件,还是剪力墙和连梁构件,都可以将地震作用下钢筋混凝土构件的复杂非线性受力变形行为和混凝土、钢筋材料的本构关系直接联系起来。因而,本工程的弹塑性分析将直接基于材料的应变对于结构构件的损伤性能水准进行评价。参考规范FEMA 356[11],表6列出了进入屈服状态后混凝土和钢材的各水准应变限值。为了应用上述指标对结构构件的损伤性能水准进行评价,在MSC.MARC软件中,基于用户二次开发功能对结构模型的地震工况计算结果进行自定义输出。将剪力墙(含连梁)、框架柱和框架梁等构件的钢筋应变和混凝土受压应变进行处理后,以损伤指标的形式输出,可通过云图进行直观显示,进而评价结构构件的性能水准。对于钢筋,定义输出损伤变量Ds=εs/εy,其中εs和εy分别为构件中钢筋经历的最大应变和屈服应变值。对于混凝土,定义输出损伤变量Dc=εc/ε0,其中εc和ε0分别为构件中混凝土经历的最大压应变和峰值应变值。根据上述损伤变量显示结果,可以清晰判别结构各构件中的钢筋是否屈服(Ds是否大于1)和混凝土是否受压达到其峰值应变(Dc是否大于1),并参照表6进一步快速评价该构件的具体性能水准。
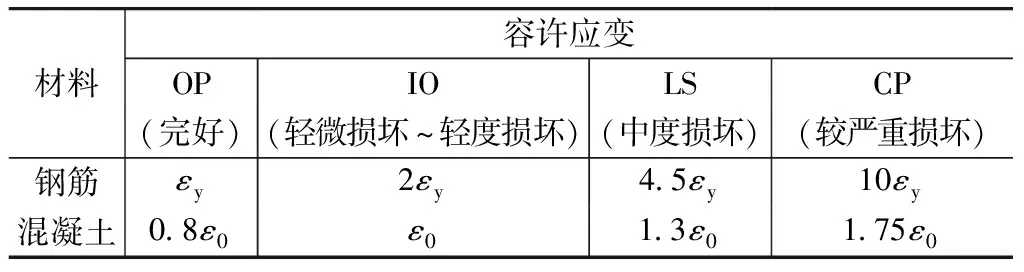
结构材料各水准的塑性应变判别标准 表6

各工况作用下主体塔楼结构各构件损伤指标Ds,Dc结果与性能水准 表7
4.3 主体塔楼结构构件损伤指标结果与性能水准评价
以天然波1为例,图12,13给出了强连接方案工况1下(水平向地震以X向输入为主)主体塔楼结构各构件损伤指标分布结果(图中颜色越深,损伤指标数值越大,代表相应的构件损伤程度越严重)。各工况作用下主体塔楼结构各构件损伤指标Ds和Dc结果与性能水准如表7所示。可以看出,在罕遇烈度三向地震作用下,所有框架柱和墙肢均处于OP性能水准,而部分框架梁和连梁则达到了CP性能水准。说明结构中的框架柱和墙肢基本处于弹性状态,而框架梁和连梁作为耗能构件,部分可达较严重破坏。从空间分布上来看,只是中间楼层的框架梁和连梁较其他楼层损伤程度较严重,达到CP性能水准,在其他楼层则为LS性能水准。这与框架-剪力墙结构体系的受力变形特征是相符的。根据强连接方案和弱连接方案的相应结果对比可见,两种方案下主体塔楼结构损伤程度差别很小,同类构件处于相同的性能水准状态。这说明上部棚架结构和下部双塔楼之间采用不同的连接方案对下部主体塔楼的地震损伤状况影响很小。
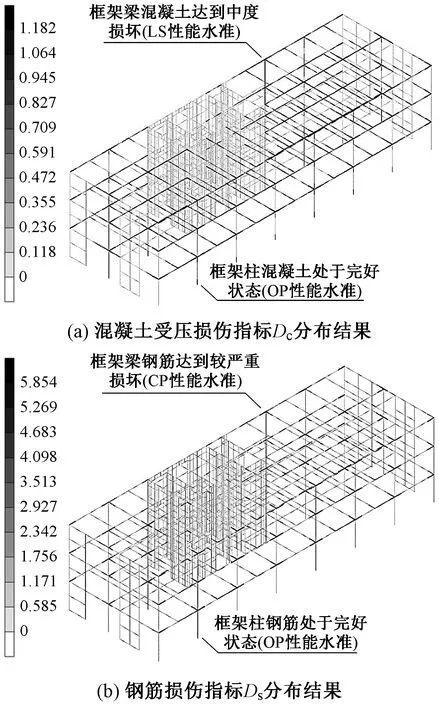
图12 框架损伤指标分布(损伤程度相对最大处为14~16层)
4.4 直接支承上部棚架的框架构件损伤指标结果与性能水准评价
对于本项目双塔结构而言,塔楼顶部的23层框架直接支承着结构的连接体(上部棚架),因此其起着连接上部棚架和下部主体塔楼的作用。该区域构件受力复杂,需要细致校核其损伤指标和性能水准。图14,15以天然波1的工况1(水平向地震以X向输入为主)计算结果为例,分别给出了强连接方案和弱连接方案下塔楼顶部支承上部棚架的框架梁、柱损伤指标Dc和Ds的分布结果(指标意义与4.3节相同)。由图14,15可以看出,在罕遇烈度三向地震作用下,采用弱连接方案时,可以有效降低连接上部棚架和下部主体塔楼的支承框架构件的损伤程度。该区域的框架梁、柱混凝土损伤指标最大值由0.695减为0.599;而更值得关注的是,在强连接方案中,该区域的框架柱有可能屈服,钢筋损伤指标最大值达2.88,达到中度损伤水准,但在弱连接方案中,由于支座水平力大大减小,使得支承上部棚架的框架柱不会屈服,为完好状态,该区域仅框架梁会发生轻微屈服,钢筋损伤指标最大值仅为1.343,为轻度损坏水准。这显示了弱连接方案在本工程中的优势。
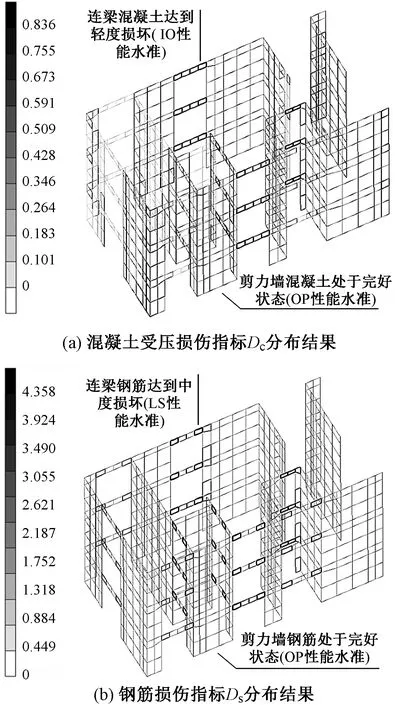
图13 剪力墙(含连梁)损伤指标分布(损伤程度相对最大处为5~7层)
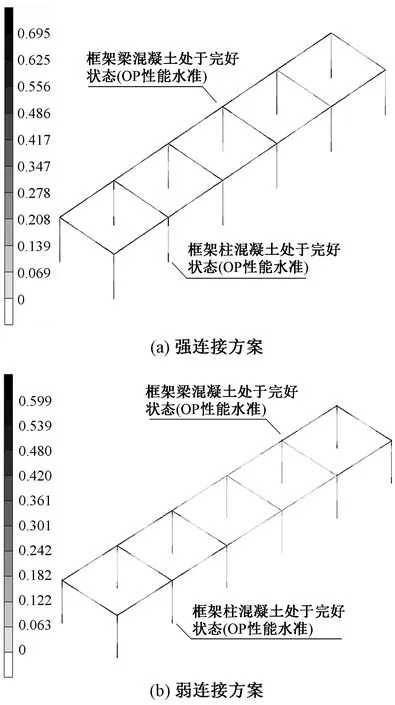
图14 支承上部棚架的23层框架构件的混凝土受压损伤指标Dc分布结果
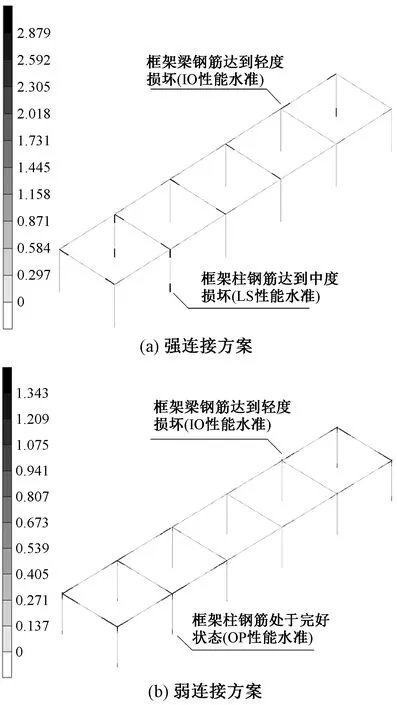
图15 支承上部棚架的23层框架构件的钢筋损伤指标Ds分布结果
5 结论
利用有限元分析软件MSC.MARC对本工程的双塔结构(含上部棚架,且分别考虑强连接和弱连接方案)进行数值模拟,基于罕遇烈度三向地震作用下的弹塑性时程分析,重点考察了结构位移、反力等结果,并基于软件的二次开发功能校核了结构各构件的损伤破坏状态和性能水准。得出以下结论:
(1)本工程双塔结构在罕遇地震作用下的弹塑性层间变形,无论是强连接方案还是弱连接方案,多条波弹塑性时程分析结果计算得到的弹塑性层间位移角参考值,均小于1/135,满足性能化设计要求。无论采用强连接方案还是弱连接方案,下部主体塔楼结构的损伤破坏模式均为“强墙肢,弱连梁”和“强柱弱梁”,且下部主体塔楼结构的所有墙肢和框架柱处于OP性能水准,而框架梁和连梁则达到了CP性能水准。
(2)总的来看,本工程上部棚架结构和下部双塔楼之间采用不同的连接方案对下部主体塔楼的各种地震响应结果影响都较小。下部主体塔楼结构在罕遇地震作用下层间变形分布较为均匀,不存在明显的薄弱层;整体结构损伤程度较小,塑性铰分布合理,耗能构件明确,竖向构件基本处于弹性状态,能满足性能设计目标D+的要求。
(3)从对支承上部棚架的框架构件受力有利的角度考虑,采用基于摩擦摆支座的弱连接方案具有优势,可以大幅减小支承柱的损伤程度。且经过计算分析,摩擦摆支座最大出力和滑移量可以满足工程设计要求。本文将摩擦摆支座应用于高位连体结构进行的弹塑性分析有关结果,可为高位连体结构采用摩擦摆进行弱连接方案的抗震设计提供参考。

