水力冲孔孔洞受压变形特征模拟研究

沈逸飞，张嘉勇，许慎

(1.华北理工大学 矿业工程学院，河北 唐山 063210；2.河北省矿业开发与安全技术重点实验室，河北 唐山 063210)

我国是世界上最大的煤炭生产国和消费国，煤炭消费接近全国能源消费总量的70%[1]。目前，全国大多数矿井均为地下井工开采，且其平均开采深度已达500 m以上，每年仍继续往下增加20 m。深部煤炭资源赋存及开采条件复杂，煤层瓦斯含量较高，50%以上的开采煤层为高瓦斯煤层，如何对高压高地应力煤层进行低成本、高效卸压増透成为了亟需解决的重要问题[2]。目前，矿井较为常用的卸压增透方法，如：水力切缝强化抽采技术、深孔控制爆破技术、旋转水力扩孔技术、密集长钻孔技术等，在防治煤层瓦斯灾害问题方面起到了一定的积极作用[3]。但是由于受到多种条件的限制，上述方法或多或少都存在着适用面较窄、成本较高等亟需解决的关键难题。高压水射流破煤增透技术相对于其他增透方法，具有技术实施安全系数高、能耗低、经济成本较小等众多有优势，在平顶山、开滦、峰峰等多个矿区的低渗透性煤层成功得到应用，积累了较多的现场应用经验[4]。

高压水射流冲孔后形成多为梨形的孔洞，孔洞在围压、地应力等作用下发生形变，煤体中大量原生裂隙在应力的作用下进一步发育[5]，进而提升煤层渗透率和瓦斯抽采效率。为探明水力冲孔后孔洞变形演化机理和规律，通过理论分析、数值模拟计算等手段，对煤体冲孔后的孔洞变形进行分析，研究其受压的状态及演变过程，为高压水射流卸压增透技术大范围推广和应用提供理论和技术支撑。

1 水力冲孔孔洞数学模型

1.1 水力冲孔孔洞变形的力学模型

高压水射流高速冲击物体表面，使其受拉伸力和剪切力作用产生破碎坑，其对煤体的作用主要包括气蚀破坏作用、冲击作用、动压力作用和水楔作用等[6,7]。水射流形成孔洞后，在围压、地应力等因素的影响下，孔洞及周围的煤体进一步发生变形和破坏。影响孔洞变形的主要因素还包括瓦斯含量、顶底板的岩性以及其自身性质等。

煤体在受压前期处于弹性阶段，在弹性状态时其变形服从胡克定律。当煤体受压达到峰值强度 后，煤体处于屈服状态，自身的强度随着应变增大逐渐衰减服从Mohr-Coulomb强度屈服准则，直至残余强度 。三线段软化模型如图1所示。

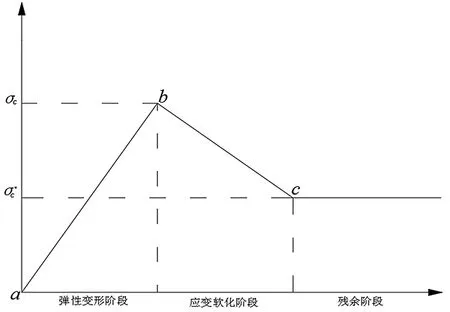
图1 三线段软化模型[8]

高压水射流成孔孔径远大于一般钻孔孔径，为此将其受力情况简化为平面应变问题进行求解，满足平面应变的平衡方程和几何方程在弹性变形区。由平衡方程、几何方程及Poyting-Thomson模型可得弹性变形区的应力及位移u方程[9]为：

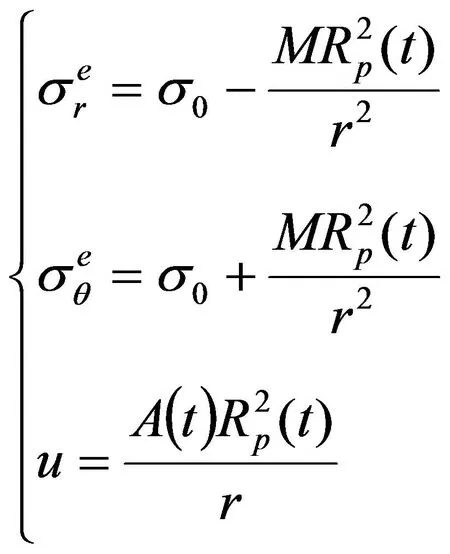
(1)

式中：R(t)为塑性区半径，A(t)为时间的函数：

(2)

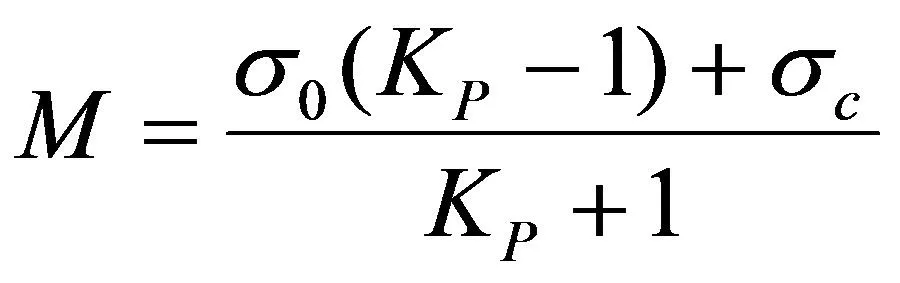
(3)

其中，G0和G∞为煤体的初始和长时间后的剪切模量；ηret为延迟时间；t为时间；Kp=(1+sinφ)/(1-sinφ)，φ为煤的内摩擦角。

高压水射流成孔后，煤体内部的孔、裂隙在地应力和瓦斯压力综合作用下，产生新的孔裂隙及裂纹，并且随着时间的增加，裂隙会扩展发育成裂隙网，为瓦斯运移提供通道，进而增大煤体渗透率，达到卸压增透的目的。

1.2 高压水射流成孔孔洞模型

工业现场试验表明，高压水射流成孔大多为椭球形孔洞，孔洞内部扩展较大而孔口处较小[10]。利用Bergmark-Roos放矿理论建立松散矿岩流动模型，将方程改进后，带入常量并采用Matlab绘制水力冲孔孔洞形态，如图2所示。

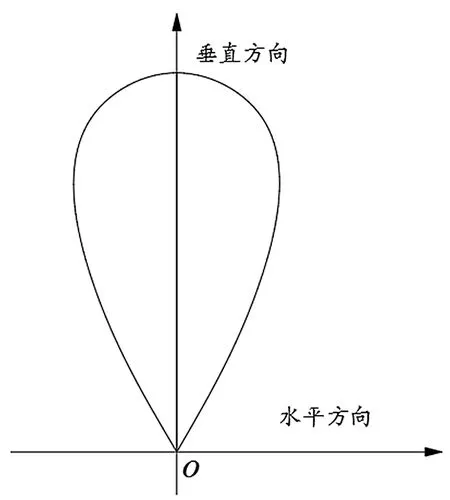
图2 水力冲孔洞形态-梨形[8]

2 水力冲孔孔洞受压变形数值模拟

2.1 数值模拟模型的建立及单元格划分

采用三维立体构建数值孔洞模型，如图3所示。依据工业现场实际情况，模型整体尺寸为3 m×3 m×10 m的长方形，孔洞为孔口小而内部大的圆台，孔洞底部为半球体，整体模型为类锥形椭球体，成孔初始孔径为0.4 m，深度为5 m，半球体半径为0.9 m。模型划分为83 077个单元格，并将孔内壁进行网格细化，单元类型采用Solid65三维钢筋混凝土实体，常规加载条件设置其顶板围岩压力为20 MPa，煤体模型主要参数如表1所示。

表1 煤体模型参数

图3 冲孔模型图

2.2 模拟结果分析

高压水射流成孔时，煤体内部结构被破坏，煤体发生破碎、剥落，孔洞内部煤层渗透率明显改善。成孔后在地应力和瓦斯压力的综合作用下，孔洞继续产生形变，变形量会随着时间的推移而逐渐增大，直到煤体发生塑性变形为止。数值模拟结果如图4和图5所示。

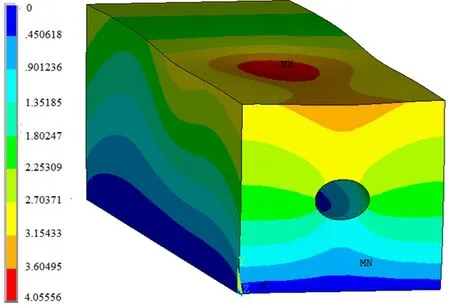
图4 整体主位移图

图5 整体主应力图

由图4和图5可知，孔洞位移变形主要集中在模型顶部中间区域，此时孔内部上下两侧区域出现最大主应力；孔洞内部因冲孔产生裂隙的煤体会在应力的作用下进一步发生形变，随着时间推移，当形变超过弹性阶段，煤体就会发生塑性变形直至到达残余强度，最终孔洞上方煤体会因破碎失稳进而坍塌，两侧应力集中部位的煤体也会发生掉落，随后被水流冲出；孔洞深部顶板出现最大位移，且位移会随着时间逐渐增大，此区域先于其他区域发生失稳塌陷现象。

3 水力冲孔范围对煤体裂隙演化规律的影响

煤单轴压缩试验结果表明，煤体受压至一定程度后会出现扩容现象，此现象产生主要原因是煤体内部发生位移产生了大量裂隙，促使煤的体积增大。虽然受压煤体在弹性变形阶段时煤体变形位移量较小，但其对后续的变形规律有很好的预测作用。为便于模拟分析计算，在研究水力冲孔范围对煤体损伤演化规律的影响时，主要研究对象为弹性变形阶段。

依据工业现场试验实际情况，结合损伤演化规律分析目的，将分析模型孔径设置为40 mm，研究水力冲孔深度分别为300 mm、400 mm、500 mm、600 mm、700 mm时，观测孔洞应力分布以及顶部区域位移关系情况，模拟结果如图6和图7所示。

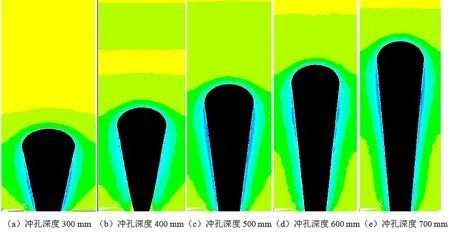
图6 孔洞截面Y向应力分布图

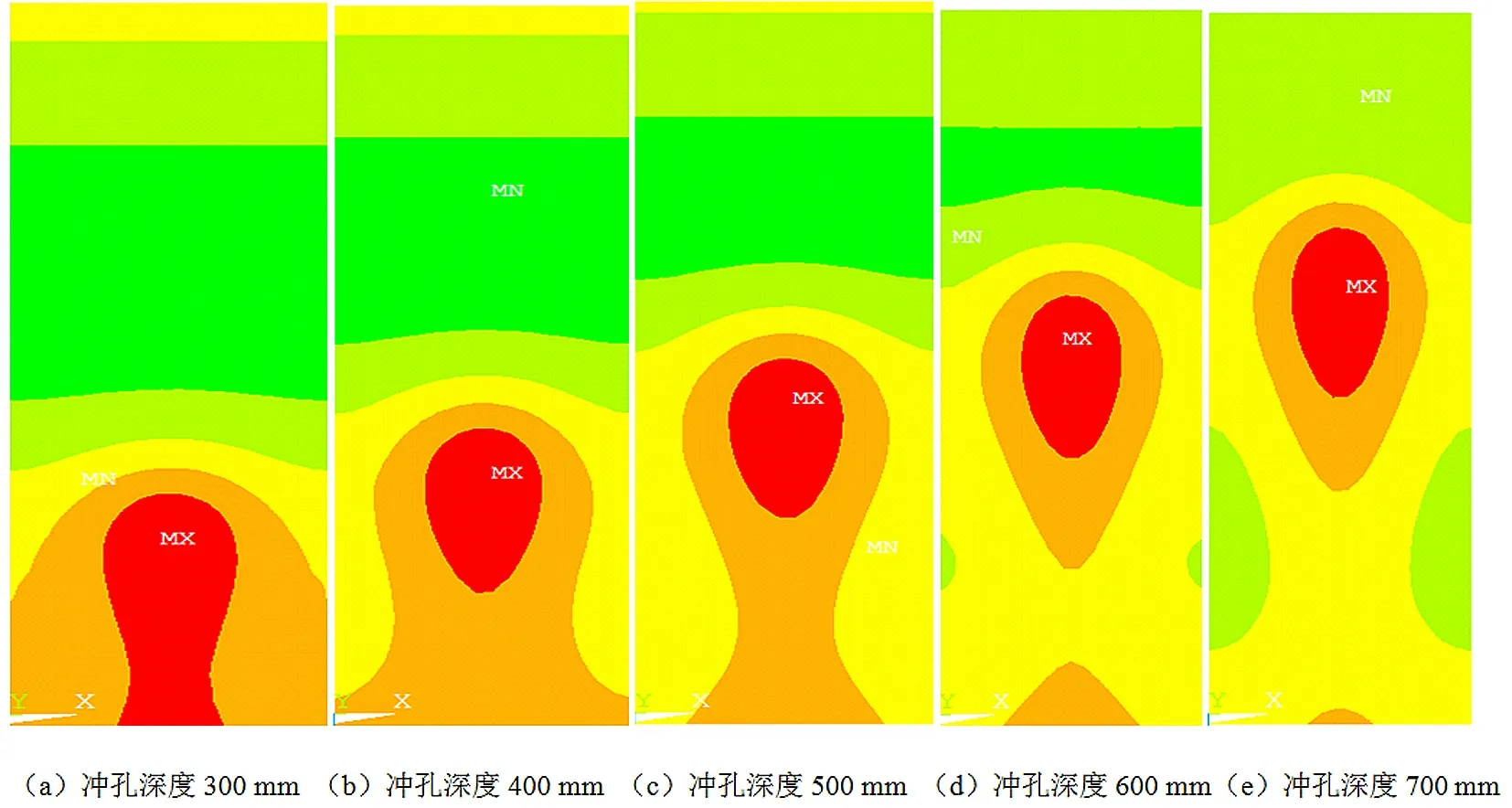
图7 孔洞顶部主位移分布图

由图6可知，此时孔洞应力集中区域主要在孔壁两侧，其区域随着深度的增加而增大，达到最深处后应力逐渐衰减。由图7可知，孔洞的顶部会产生位移集中区，且随着孔深增加。位移变形集中区域会向深部转移，随着深部位移变形量的增加，可能发生孔洞坍塌现象。综上所述，冲孔成孔越深，在应力的作用下深部区域发生坍塌的可能性进一步增加。因此，卸压增透成孔深度要在合理范围内，成孔深度过大会造成塌孔现象，导致煤体内部瓦斯运移通道闭塞，进而影响煤层整体卸压增透效果。

为进一步研究冲孔深度对煤体裂隙发育的影响规律，将成孔深度的孔洞截面Y向应力与顶部区域主位移变形量进行对比分析，绘制孔洞顶部位移和孔侧Y向应力随孔深的变化关系图，如图8所示。

从图8可知，冲孔深度300 mm时，其顶部最大位移为3.76 mm；冲孔深度400 mm时，其顶部最大位移为3.83 mm，同比增长1.8%；冲孔深度500 mm时，其顶部最大位移为3.92 mm，同比增长2.3%；冲孔深度600 mm时，其顶部最大位移为4.01 mm，同比增长2.2%；冲孔深度700 mm时，其顶部最大位移为4.11 mm，同比增长2.5%。此外，孔洞顶部区域主要位移量呈现随成孔深度增加而迅速增大的变化规律，且在孔洞的中后部区域达到最大位移量，形成凹陷区域，此区域在煤体进入可塑性变形阶段时，位移量会迅速增加直至孔洞塌陷。

4 理论出煤量与最大位移的关系

孔洞出煤量是指高压水射流冲孔过程中从煤体破碎剥离后伴随水流冲刷到巷道中的煤质量，也作为高压水射流卸压增透效果考察的重要判定指标之一，因此，有必要分析出煤量与孔洞变形位移的关系，进一步明确高压水射流卸压增透最佳参数范围[11]。此次孔洞出煤量计算是利用不同模型尺寸计算出理论的煤量，在工业现场冲孔试验时，煤破碎后会和水形成煤水混合物，易在孔的内部堆积，导致实际冲出的煤量要小于理论出煤量。模型尺寸计算是通过冲孔半径和深度，计算圆台体积和半球的体积，两者相加为成孔体积，即理论出煤体积，再用体积和密度之积即可算出理论出煤量，计算公式如(4)所示。

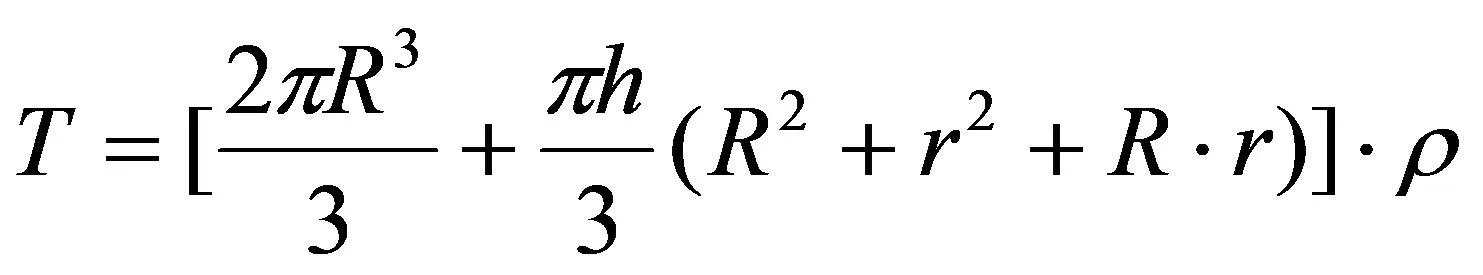
(4)

式中：T—出煤量，t；ρ—煤的密度，kg/m3；R—圆台底部半径及半球的半径，mm；r—圆台顶部半径，mm；h—圆台高度，mm。

此次出煤量与孔洞最大位移量之间的关系表现为：当计算孔径为40 mm时，孔深分别为300 mm、400 mm、500 mm、600 mm、700 mm；孔深为500 mm时，孔径分别为20 mm、30 mm、40 mm、50 mm、60 mm的理论出煤量，然后将上述不同孔径参数带入分析模型中进行数值模拟计算，确定不同孔洞参数时孔洞顶部最大位移量。统计模拟分析数据，如图9所示。

图9 理论出煤量与最大主位移的关系

由统计结果可知，理论出煤量与最大主位移总体上呈正相关，成孔孔径、冲孔深度的变化致使出煤量增加时，孔洞的体积必然增大，孔洞的最大主位移量增大，煤体结构破碎程度随之增大。此时煤体内部支撑应力发生剧烈变化，煤体不稳定性增加，当煤体进入塑性变形阶段时，整体位移变化会更加剧烈，煤体进一步发生破碎变形，直至孔洞会发生垮塌。

综上所述，高压水射流成孔后会增加了煤体暴露面积的同时，进一步创造了煤层内部瓦斯流动条件；在地应力的作用下，破碎的煤体会进一步发生位移，使得煤体内的裂隙充分发育。但需要注意的是，冲孔深度需控制在合理的范围内，确保孔洞顶部位移变形量维持在合理范围内，防止孔洞蠕变甚至坍塌，致使煤层渗透率降低的同时发生顶底板灾害事故。

5 结论

(1)高压水射流成孔后，在孔洞内部左右两侧区域出现应力集中区，其应力大小随着深度的增加而增大，达到最深处后应力逐渐衰减。上下两侧出现位移集中区，位移变形主要集中在孔洞顶部中间区域。随着孔深增加，位移变形集中区域会向深部转移，最大位移量随成孔深度增加而增大，冲孔深度每增加100 mm，其顶部最大位移变形量会增加1.8%～2.5%。

(2)冲孔出煤量与孔洞顶部最大主位移量呈正相关，在一定范围内，出煤量越多，孔洞顶部下沉位移越大，二者相关度R2=0.95。因此需要合理确定冲孔成孔参数(出煤量)，通过防止煤体结构失稳，从而减少顶底板灾害事故的发生风险。

SimulationonDeformationCharacteristicsofHydraulicPunchingHolesunderPressure