基于EMD和PCA的滚动轴承故障诊断研究

史东海，王洁，崔诚

基于EMD和PCA的滚动轴承故障诊断研究

史东海，王洁，崔诚

（沈阳工业大学 机械工程学院，辽宁 沈阳 110027）

为了对滚动轴承的工作状态以及故障类别得到准确的诊断，文章通过对滚动轴承的信号进行经验模态分解（EMD）并提取信号的时域、频域特征构成高维数据集，然后对数据集进行主成分分析（PCA）降维处理，并结合K近邻（KNN）分类算法对结果进行准确分类，最终实现滚动轴承的故障诊断。结果表明，该方法能够针对滚动轴承振动信号得到准确的状态诊断。

滚动轴承；故障诊断；经验模态分解；主成分分析

前言

滚动轴承广泛应用于制造行业的各类大型器械制造中，其在机械运行过程中起着不可替代的重要作用，因此针对滚动轴承的故障诊断就显得尤为重要。在滚动轴承进行故障诊断的过程中，由于受到噪声信号的干扰，诊断的准确性往往不尽如人意[1]。因此，确定一种能够准确诊断滚动轴承故障的方法具有非常重要的意义。

滚动轴承的信号往往是复杂、无序的，仅仅提取其相应的时域、频域特征无法充分得到信号的特征。而EMD[2]在信号数据特征提取方面的应用使这一方面的缺陷得到了填补。复杂、无序的信号在经过EMD分解后能够得到一连串的本征模态分量（Intrinsic Mode Function, IMF），这些分量包含了信号的不同特征尺度，因此能够使信号的特征在不同的分辨率下显示出来。

信号经过EMD分解和时频域特征提取后得到的特征集虽然能够非常全面地反映信号的特征，但是由于特征集的维数过高，其中的大量特征包含许多无用信息，这对后续的故障识别造成了非常不利的影响，因此需要使用数据降维方法对高维特征集进行降维处理。主成分分析[3]（Principal Com- ponent Analysis, PCA）作为一种常见的数据降维方法，拥有出色的降维处理能力，被广泛地应用到数据降维当中。经过PCA处理后的高维数据，既能保留数据的主要特征，又可以降低数据的维度。

通过以上分析，本文提出一种将EMD分解和PCA降维进行结合的滚动轴承故障诊断方法。通过这两种结合方法对信号的处理后使用K近邻（K-nearest neighbor, KNN）分类算法[4]进行模式分类，应用实例表明，该方法成功实现了滚动轴承故障的准确诊断。

1 EMD分解

EMD方法是由HUANG[5]等人在1998年提出的一种信号分解方法。该方法认为任何一个获取的特征信号都可以分解为多个本征模态函数（IMF），同时每个 IMF也有自己的要求，必须满足以下几个定义[6]：

（1）在整个实数域或复数域中，极值与零交叉点的数量最多相差一个。

（2）在函数上的任一点，信号的上、下包络线所构成的平均包络值必须为零。

经验模态分解方法的具体步骤如下：

（1）识别信号()的所有局部极大值和极小值，并用三次样条线插值局部极大值和极小值，形成上下包络线。

（2）求出上下包络线的均值1，计算信号()与1的差值1：

()−1=1（1）

如果1满足IMF的两个条件，则将其设为()的第一个IMF分量。

（3）如果1不满足条件，则将其作为原始信号，重复步骤（1）和步骤（2）：

1−11=11（2）

经过k次计算直到得到能够满足条件第一个IMF分量1k：

1(k−1)−1k=1k（3）

将1k记作1：

1=1k（4）

（4）从()中将IMF分量1分离出来：

()−1=1（5）

（5）将1作为原始信号重复上述步骤，以此获得其他的IMF分量2，3，...，c，这些IMF分量均满足：

r−1−c= r（6）

当r成为一个不能再继续提取IMF的单调函数时，分解停止。

（6）可以看出，原始信号可以用将所有的IMF和剩余的r相加来表示，即：

()=∑ =1c+r（7）

式中，r为残差。

原始信号经过EMD分解按照特征时间尺度从小到大的顺序依次分离获得一系列IMF分量，这些分量包含了信号中从高到低不同频率的信息。

2 主成分分析

针对提取到的高维特征集，主成分分析能够提取特征集中的主要特征，从而降低维数以方便后续的模式分类。对于中心化后的高维特征集，其中含有样本x，=1，...，，且∑=1x=0，计算协方差矩阵：

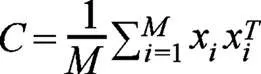
计算上式中的特征值以及特征向量：

=（9）

将求得的按从大到小排列，则其对应的特征向量也将按降序排列。主成分分析通过选取前面占比重较大的特征向量来代表整个数据，以此完成对高维数据的降维。

3 故障诊断方法步骤

基于EMD分解和PCA的滚动轴承故障诊断步骤如下。

（1）EMD分解及时频域特征提取。提取振动信号的16个时域特征和13个频域特征，其中时域特征有均值、均方根值、方根幅值、峭度、波形指标和峰值指标等，频域特征有均方频率、频率标准差、中心频率等[7]。然后，结合EMD分解得到的前5个IMF分量的能量特征平方和，组成高维特征集。

（2）数据降维。使用主成分分析对高维特征集进行降维处理。

（3）模式分类。使用KNN分类算法对降维后的特征进行分类。

4 试验验证

4.1 数据分析

本文使用美国凯斯西储大学电气工程实验室的滚动轴承振动数据进行分析[8]。电动机传动轴端的SKF6205深沟球轴承，损伤尺寸为0.177 8 mm。分别针对滚动轴承的内圈故障、滚子故障、外圈故障和正常状态进行信号截取，采样频率为1 200 Hz，数据样本长度为2 048。四种状态下的信号时域波形图如图2所示。从图中可以看出，在滚动轴承出现故障时，其波形出现规律性的幅值突然升高，而正常状态下的波形幅值变化缓慢且没有规律。

图2 滚动轴承四种状态下信号的时域波形图

4.2 数据降维分析

针对轴承提取到的高维特征使用主成分分析进行降维处理，四种状态各选取50组样本，其中各选取30组样本作为训练样本，然后选取各20组样本作为测试样本，经过降维处理的样本如图3所示。

图3 经过PCA降维处理的结果

从图中可以看出，经过EMD和PCA方法后，信号四种状态下的特征分散在四处，每个状态之间都没有任何混淆，由此可见此方法针对滚动轴承信号的处理非常实用。

4.3 KNN算法分类

针对经过EMD和PCA处理后的样本，使用KNN分类算法进行分类，经过分类后可以直接看到分类的准确程度，分类结果如图4所示。

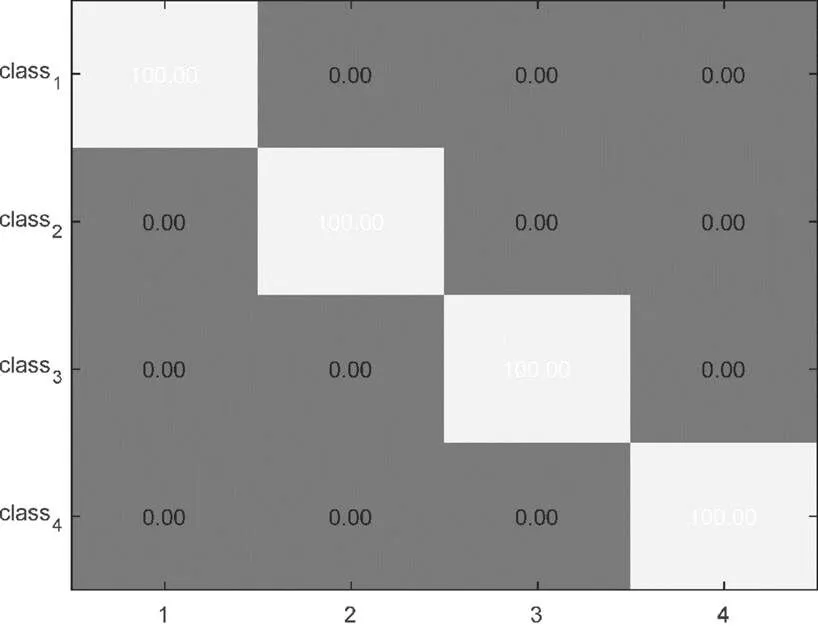
图4 KNN分类结果

从分类图中可以看出，每个分类的准确率都为100%。由此可知，EMD提取和PCA降维处理方法能够高效对滚动轴承信号的特征进行处理，与KNN分类算法结合后能够有效实现对滚动轴承的故障诊断。

5 结论

（1）EMD分解能够将滚动轴承的故障信号分解为含有不同特征尺度的本征模态分量，结合信号相关时频域特征后能够集合信号的大部分重要特征。

（2）针对从信号中提取到高维特征集，经过PCA降维处理后能够保留信号的有效特征，结合KNN分类算法可以实现滚动轴承的故障诊断。

[1] 李思琦,蒋志坚.基于EEMD-CNN的滚动轴承故障诊断方法[J].机械强度,2020,42(05):1033-1038.

[2] 徐晓刚,徐冠雷,王孝通,等.经验模式分解(EMD)及其应用[J].电子学报,2009,37(3):581-585.

[3] 吉敏.基于PCA-SVM的轴承故障诊断研究[J].电子设计工程, 2019,27(17):14-18.

[4] 李宏志,李苋兰,赵生慧.基于Spark的大规模文本KNN并行分类算法[J].湖南科技大学学报(自然科学版),2020,35(01):90-97.

[5] Huang N E, Shen Z, Long S R, et al. The empirical mode decomposi- tion and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society of London. Series A: mathematical, physical and engineering sciences,1998, 454(1971):903-995.

[6] 张颖,马波,张明,等.基于EMD和PCA的滚动轴承故障信号特征提取研究[J].机电工程,2015,32(10):1284-1289.

[7] 马萍,张宏立,范文慧.基于局部与全局结构保持算法的滚动轴承故障诊断[J].机械工程学报,2017,53(02):20-25.

[8] The Case Western Reserve University Bearing Data Center Bearing data center seeded fault test data[EB/OL]. [2020-10-21].http://cse- groups.case.edu/bearingdatacenter/ pages/download-data-file.

Research on Rolling Bearing Fault Diagnosis Based on EMD and PCA

SHI Donghai, WANG Jie, CUI Cheng

( School of Mechanical Engineering, Shenyang University of Technology, Liaoning Shenyang 110027 )

In order to get an accurate diagnosis of the working condition and the fault category of rolling bearings, a high-dimensional dataset is formed by performing empircial mode decomposition on the signals of rolling bearings and extracting the time-domain and frequency-domain features of the signals, and then performing principal component analysis to reduce the dimensionality of the dataset, and combining with the K-nearest neighbor classification algorithm to accurately classify the results, finally realising the diagnosis of rolling bearings fault diagnosis. The results show that the method is able to obtain accurate condition diagnosis for rolling bearing vibration signals.

Rolling bearing; Fault diagnosis; Empircial mode decomposition; Principal component analysis

TH133.33

A

1671-7988(2021)23-94-03

TH133.33

A

1671-7988(2021)23-94-03

10.16638/j.cnki.1671-7988.2021.023.026

史东海，硕士，就职于沈阳工业大学机械工程学院。