城市轨道交通系统动态风险模态分析建模

范博松，邵春福

（北京交通大学，综合交通运输大数据应用技术交通运输行业重点实验室，北京 100044）

0 引言

近年来，城市轨道交通的快速发展极大地满足了城市化的发展需求，成为解决城市交通拥堵的有效方案。但是伴随大规模路网的兴建，城市轨道交通的运营与管理安全问题也逐渐显现。

模糊理论[1]和层次分析法(AHP)[2]被广泛应用于城市轨道交通系统静态风险评价。Fang 等[3]将多层决策树与模糊分析的思路结合起来提升轨道交通的运营安全，通过克服数据主观性和变量独立性的不足，确定影响轨道交通突发事件的风险因素。周雯等[4]采用层次分析法和灰色系统理论分别开展了风险指标的层次分析和权重计算，并融合两者的计算结果，综合评价确定了风险水平。以上的风险分析方法能在一定程度上得到评价结果，但都局限于对过去某一时刻的风险评价，不能很好地反映风险的动态特征。

动态风险是风险考虑时间变化特征的延伸。Wang等[5]以火灾事故为研究对象，采用ETA进行风险事件分析，并利用贝叶斯理论进行动态的疏散分析。Wu 等[6]利用贝叶斯网络构建地铁车站火灾事故原因、紧急措施和后果的关系网，提出了动态风险评估的有效工具。Liu 等[7]对城市轨道交通系统的脆弱性进行仿真，分析动态风险评估中的关键影响因素。以上分析虽然引入了动态风险的思想，但大都忽略了风险动态变化的时间跨度，并没有明确地从时间维度进行剖析。

复杂网络主要用于研究各种系统微观状态和宏观现象之间的密切联系，特别是在网络结构的形成机理、演化方式和动态行为等方面有较强的优势。Yang 等[8]利用复杂网络评价了城市轨道交通网络在受到攻击时的鲁棒性，并展示了网络的拓扑变化特性，协助轨道交通的安全管理。基于级联失效模型和复杂网络理论，Liu[9]等分析出重要度高的节点失效，城市轨道交通网络的抗毁性较弱，以此进行针对性防控。为了分析城市交通拥塞风险演化机理，Hu[10]等利用复杂网络节点重要度理论识别出核心节点，通过免疫控制较好地限制了风险传播。以上研究将地铁站点视为复杂网络节点，受限于地铁线网的拓扑特性，风险分析不具有较强的普适性。

本文采用复杂网络建模的思想对城市轨道交通系统突发事件进行动态风险分析，将突发事件的风险因素、滞后时间长度、事件等级三者融合为抽象的风险模态，以此表征网络图模型的节点。进而利用网络节点强度的观点，分析城市轨道交通系统的动态风险特性，确定关键风险因素和对应的滞后时间，为城市轨道交通系统的动态风险控制措施制定提供理论和技术支撑。

1 数据分析

本文的基础数据来源于2017年北京市轨道交通路网数据，包括轨道交通每日的列车运行信息、客流信息、满载率信息以及突发事件信息等。其中，突发事件以北京市轨道交通路网数据提供的影响行车情况的事件作为分析对象，突发事件的延误信息以1 min 为单位进行记录，将每日“5 min 及以上延误事件”发生的次数作为风险等级划分标准。

突发事件所关联的风险因素主要来源于北京市轨道交通路网数据所包含的影响行车情况的因素，包括路网客运量、实际开行列数、开行方案兑现率等25 个指标，这些指标涵盖了“人员、设备、管理”等故障因素；从外部环境数据中选取轨道交通股票金额、重大活动及节假日和天气这3 个指标，从这28 个指标入手对轨道交通风险状况进行分析，具体指标如表1所示。

表1 28个风险因素指标描述Table 1 28 risk factors and their descriptions

2 模型构建

2.1 复杂网络

与传统的图模型类似，复杂网络主要包含节点和边(弧)两种要素，按照预设或观测的结构将节点和边组合成复杂网络的对应关系，其数学表达式为

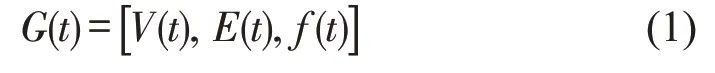
式中：G（t）为t时刻的网络图；V（t）为t时刻网络中的节点集合；E（t）为t时刻网络中的边集合；f（t）为t时刻网络中节点与边的映射关系。

度及度分布是复杂网络的基础概念。在网络中，度是指与某一节点相邻节点的数量，即与某一节点直接相连的边的数量。作为分析网络中不同节点重要性的基本依据，通常关注网络中度值最大的节点，通过分析少量样本特性推知整个网络的规律。

2.2 动态风险

动态风险为风险因素与结果随着时间变化使得动态风险模态发生变化的过程。为了能够较好地衔接风险因素与结果状态，本文引入“因素对可能结果的影响状态”指标进行过渡。风险模态定义为系统在每一时间点上3种状态信息的逻辑组合，即风险因素状态F，因素对可能结果影响状态I和可能事件等级C三者的组合，也反映了风险的形成机理。其中，F取28个风险因素指标的数值，I为滞后时间长度，C为“5 min 及以上延误事件”发生的次数。风险模态的结构如图1所示。

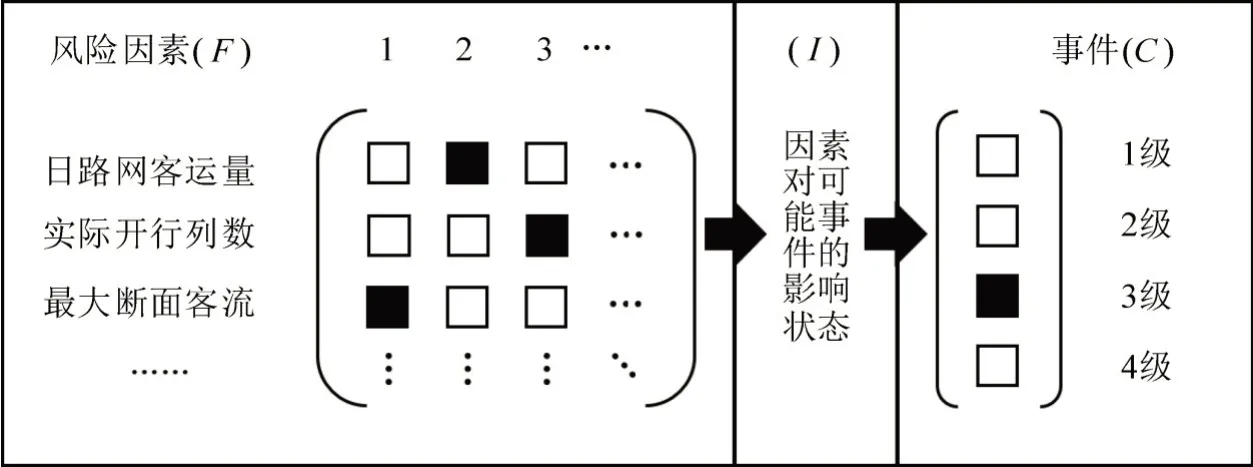
图1 风险模态信息的组合Fig.1 Combination of risk mode information

本文构建动态风险系统为：在任一时刻t，动态风险系统存在n个风险因素{xp|p=1,2,…,n} ，每个风险因素状态用xp（t）表示，整个状态集合用S（t）表示，其中p表示研究对象为n个风险因素中的第p个；n个风险因素对其特定事件C（t）可能的影响状态用I（t）表示，不同影响状态的等级用y（t） 表示，而特定事件C（t） 所包含的各类情况用{cq（t）|q=1,2,3,4} 表示，其中q表示事件所包含的4种等级。这样，时刻t动态风险模态M（t）的基本形式为

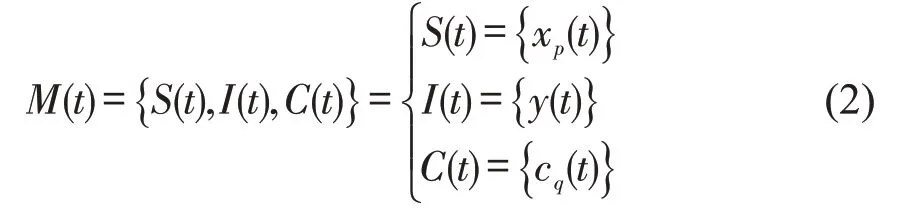
其中，每个风险因素状态xp（t）对应于一段时间内的k个变化取值，即

式中：Δt为单位时间间隔。

风险因素与事件之间的相关关系具有非同步性，为了限定分析区间并通过比选得到关键风险因素状态指标，故采用“双时间窗”的思路寻找特定时间节点异步相关关系最紧密的风险因素以及相对应的滞后时间。“双时间窗”包含主时间窗D和副时间窗d，并设定时间窗的单位移动步长Δt，进而计算各风险因素和相应结果在不同时间滞后水平L（L∈N+）下的异步相关关系，如图2所示。主时间窗D根据时间序列的周期性进行设定，副时间窗则由主时间窗和最大时间滞后水平确定，d=D-maxL+1。

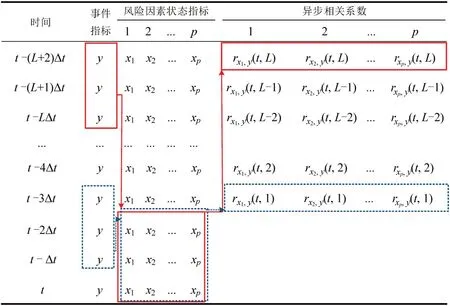
图2 不同时间滞后水平下的异步相关系数计算表（L ∈[1,5]）Fig.2 Asynchronous correlation coefficient calculation table at different time lag levels（ L ∈[1,5]）

t时刻的异步相关系数计算方法为

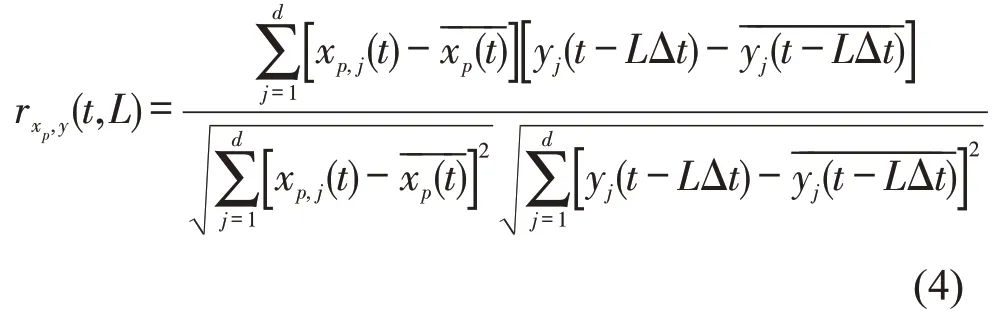
式中：j为副时间窗d中的第j个值。

根据相关系数的含义可知，若rxp,y越接近于1(-1)，则风险因素对结果的影响程度越大，且两者之间的正(负)相关关系越显著，同时L越小，则可能的影响程度也越紧迫。即 |rxp,y|越大，L越小，则该风险因素越关键。为了能够更加准确地寻找到处于不同时间节点的关键风险因素，本文引入相关性-时间敏感系数作为筛选标准，拟通过定量的方法衡量相关关系和时间滞后水平两者的相互作用，并求得在任一时间t和给定的时间滞后水平L下各风险因素敏感系数的最大值，即

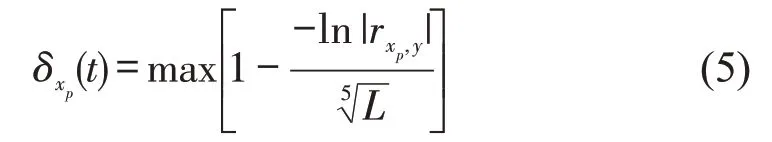
式中：δxp（t）的取值范围为[0,1]。

根据上述分析，可以得到相关关系rxp,y和相关性-时间敏感系数δxp（t），还从计算结果中得到对应的关键风险因素xp（t）和时间滞后水平L(其中，L能集中体现多种元素对结果的影响特征，因而选取L代表I（t）)，而这两者可以反映相关系数和敏感系数的特点。

2.3 动态风险到复杂网络的映射

动态风险模态M（t）={x1（t）,Lx1（t）,c2（t）} ,M（t+1）={x8（t）,Lx8（t）,c3（t）} ，表示t时刻的关键风险因素x1，经过Lx1时长的时间滞后，可能会在t+1时刻诱发3 级严重程度的结果。本文xp（t）的取值个数为28，对应28个关键风险因素；Lxp（t）为关键风险因素xp对应的滞后时间长度，取值区间为1～5 d；cq（t）为关键风险因素可能导致的事件状态的等级，共有1、2、3、4级。

在动态系统中，随着时间的变化，各动态风险模态相互转化，形成了复杂的动态风险模态演化拓扑关系。在拓扑关系中，将动态风险模态作为复杂网络的节点，将动态风险模态之间转化的连接作为复杂网络的有向边，并把两个相同的动态风险模态之间的转化频次记作复杂网络两节点间有向边的权重值。动态风险模态演化与复杂网络的对应关系如图3所示。

根据图3的映射结果，构建基于复杂网络的有向权重动态风险模型，用DWRN 表示。根据数据的时序波动特性，设定主时间窗长度D=7，最大时间滞后水平maxL=5，则副时间窗长度d=3。将数据代入理论模型，构建出基于本文数据集的有向权重动态风险模型，如图4所示。其中节点颜色越深、半径越大表示节点的连接越多，边的宽度越宽表示节点转化的频次越高。

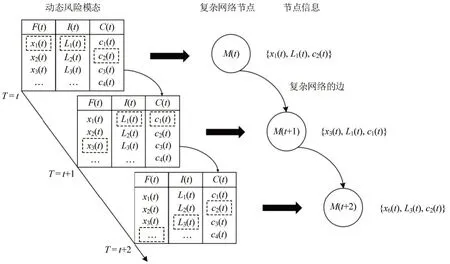
图3 动态风险模态的时间变化和复杂网络的映射过程Fig.3 Time variation of DRM and mapping process of DRM to complex networks

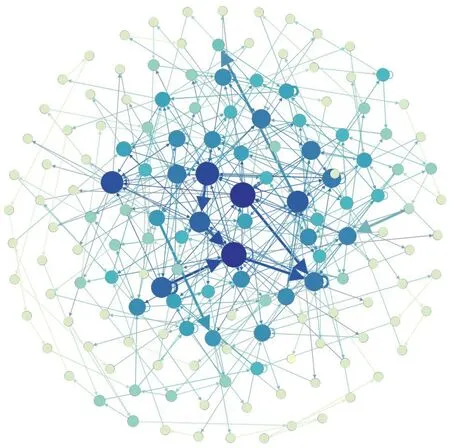
图4 轨道交通复杂网络的有向权重动态风险模型图Fig.4 Directed weighted dynamic risk diagram of complex rail transit network

3 模型应用及分析

根据D=7 和maxL=5，总计365 个数据点的每个指标时间序列，通过双时间窗处理后，形成359个主时间窗片段，对应于DWRN模型中359个动态风险模态。经过统计分析，DWRN 模型包含的不同动态风险模态为140 种，即对应于模型中的140个不同的节点。

根据动态风险到复杂网络演化的拓扑关系，可以给出DWRN模型的数学表达式为

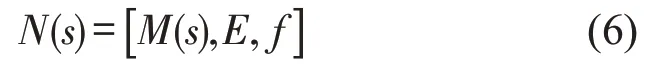
式中：N（s）为网络模型；M（s）为网络中的节点集合，包含s种节点强度；E为网络中的边集合；f为网络中节点与边的映射关系。

在t时刻网络内部节点的关系可表述为

式中：Mp0（s,t） 为t时刻网络中的第p0个节点；Mp1（s,t）为t时刻网络中的第p1个节点；Ep0,p1（t）为t时刻第p0个节点与第p1个节点之间的关系。

依据复杂网络中度的含义，在DWRN 模型中引入节点强度的概念。节点强度主要反映节点间的传递演化综合水平，定义为节点与邻居节点间连边的权重和W，公式为

式中：p为节点p0的邻居节点的集合；wp0,p1为节点p0与邻居节点p1之间边的权重值。节点强度越大，对应在DWRN模型中该节点越关键。图5为计算得到的动态风险模态节点强度图。

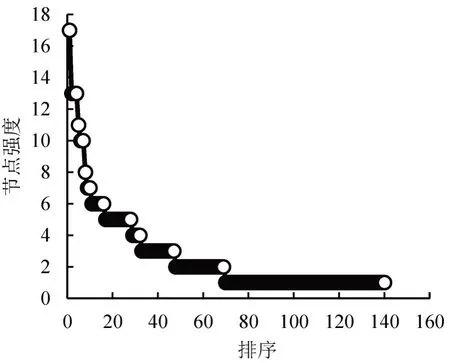
图5 动态风险模态节点强度图Fig.5 DRM node strength diagram

由图5可知，140 个风险模态中，前28 个(占比20%)重要风险模态，在381次动态演化过程中承担了53.81%的传递作用，如表2所示。

表2 重要动态风险模态统计分析Table 2 Statistical analysis of important DRM

通过计算动态风险系统的节点强度，得到需要重点关注的动态风险模态。动态风险模态的关键风险因素、滞后时间长度和结果等级如表3所示。表中事件等级4、3、2、1级分别代表路网当天5 min延误次数分别落在区间[4,+∞）,[2,4）,[1,2）,[0,1），其中1级代表安全状态。

表3 动态风险模态关键信息统计分析Table 3 Statistical analysis of DRM key information

4 结论

本文基于复杂网络的动态风险建模方法，对城市轨道交通系统进行动态风险分析。模型融合关键风险因素、风险因素对结果的影响、事件等级这3个风险管控要素，通过定义动态风险模态，采用相关性-时间敏感系数指标分析风险因素与结果等级的显著性，进而得到动态风险模态三要素的关系。通过将风险模态定义为节点，将风险模态转化定义为有向边，在动态风险系统与复杂网络之间构建起有效的映射关系。

对案例结果分析可知，部分节点强度大的动态风险模态在整个动态风险系统的演化过程中起到了主导作用，显示出网络模型能够较好地反映动态风险系统的演化特性。在整个动态风险系统中，具有3 级动态风险模态的关键风险因素为“正点率”“天气”，平均滞后时间长度为2.71 d；具有2级动态风险模态的关键风险因素为“实际开行列数”“重大活动及节假日”，平均滞后时间长度为2.9 d。因而在日常城市轨道交通系统运营过程中，管理人员应重点关注这4个关键风险因素，并在滞后时间长度内采取必要措施。