城轨线路列车时刻表与车站客流控制协同优化方法

卢亚菡，杨立兴，孟凡婷，夏东阳，戚建国

（北京交通大学，a.轨道交通控制与安全国家重点实验室；b.交通运输学院；c.综合交通运输大数据应用技术交通运输行业重点实验室，北京 100044）

0 引言

近年来，我国城市轨道交通发展迅猛，截至2019年底，已有40个城市开通运营轨道交通，其中19 个城市已实现网络化运营[1]。网络化运营极大地提高了出行可达性，从而吸引了大量通勤客流，给运营组织带来了极大的挑战。特别是早晚高峰时段，车站客流大量聚集，导致列车持续过载、站台拥堵情况严重。考虑到客流时空分布与列车运行时刻表密切相关，为缓解上述问题，各大城市分别从供给侧和需求侧进行调控。供给侧方面，主要通过缩短高峰期发车间隔以提高运力；需求侧方面，多采取高峰期常态化限流的管理措施，通过控制单位时间内进站客流量，进而减少站台聚集人数。以北京地铁为例，2019年工作日日均进站量达654.1万人次，换乘量超500万人次，全年共有10条线路15 次缩短发车间隔，91 座车站实施常态化限流措施[2]。

鉴于此，如何应对客流拥堵问题成为运营管理部门和众多学者关注的焦点。其中，黄倩等[3]以最小化乘客滞留时间和最大化运送客流量为目标，提出单线多站协同客流控制模型，并设计遗传算法求解满意的控制策略；Shi等[4]将研究的时间范围离散化，针对单条线路各站的站外到达客流，构建最小化乘客等待时间及客流聚集风险的双目标整数规划模型；石俊刚等[5]以客流预警值最小为目标，提出以安全为导向的地铁单线客流协同控制模型，并利用CPLEX软件进行求解；杨陶源等[6]建立了地铁单线列车跳站与客流控制协同优化模型，并设计基于灵敏度分析的算法进行求解；Meng等[7]以最小化乘客总等待时间为目标，研究客流需求不确定时地铁单线鲁棒客流控制问题，并设计拉格朗日松弛算法求解鲁棒模型。然而，以上文献仅考虑站外到达客流，与实际偏差较大。目前，考虑换入客流影响的相关理论研究仍处于起步阶段，比如，李佳杰等[8]分析了乘客换乘走行过程，并建立了面向换乘车站的客流控制与列车时刻表非线性协同优化模型；吴开信等[9]针对客流控制问题，将换入客流折算为站厅到达乘客，统一进行控制。然而实际中换入客流一般不经过站厅，难以进行统一控制。

综上所述，既有研究大多仅探讨了面向单一车站或单条线路站外到达客流的控制方法，忽略了换入客流对本线的影响；面向整条线路或网络，考虑换入客流影响的列车时刻表和客流控制协同优化的研究近为空白。在实际运营中，就部分换乘站而言，换入客流量远超站外到达客流量。因此，随着很多城市轨道交通成网，仅考虑站外客流，针对单站或单线的站外客流进行管控，对于缓解高峰期城市轨道交通网络拥挤现状作用有限。鉴于此，有必要从城市轨道交通系统全局角度出发，综合考虑换入客流和站外到达乘客，分析车流和客流之间的耦合关系，构建列车时刻表和客流控协同优化模型，以精准匹配运力运量，实现运营服务和运营效益双赢的目标。

1 问题描述

针对高峰期轨道交通车站过度拥挤问题，以高峰期乘客过载的轨道交通线路为研究对象，考虑邻接线路换入客流的影响，通过协同优化轨道交通线路列车时刻表与客流控制策略，尽可能地减少乘车延误人数。如图1所示，本文研究对象为主线路1，即图1(a)，该线路具有图1(b)普通车站和图1(c)换乘车站两种类型，其中，普通车站仅有站外到达客流，换乘车站的客流则由站外到达和换入客流两部分组成。站外到达乘客需在站厅排队，等待进站指令；换入乘客可直接走行至线路1 的站台等待上车。考虑线路2、3、4 换乘至主线路1 乘客的影响，调整线路1 的列车时刻表，使得线路1 列车的到站时间与邻线列车的到站时间差接近换乘走行时间，则可使换入乘客尽量直接上车，减少站台聚集人数以降低风险。为保证站台安全，需辅以客流控制策略。所谓“客流控制”，需遵循“先控制进站客流，后控制换乘客流”的运营原则，通过控制站外到达乘客的进站人数，保证换入客流优先乘车的同时避免大量乘客涌入站台，从而降低运输组织压力。此外，从系统优化角度而言，协同优化主线路列车时刻表与客流控制策略，可以精准匹配运力运量，从根本上缓解高峰期沿线车站拥挤问题。

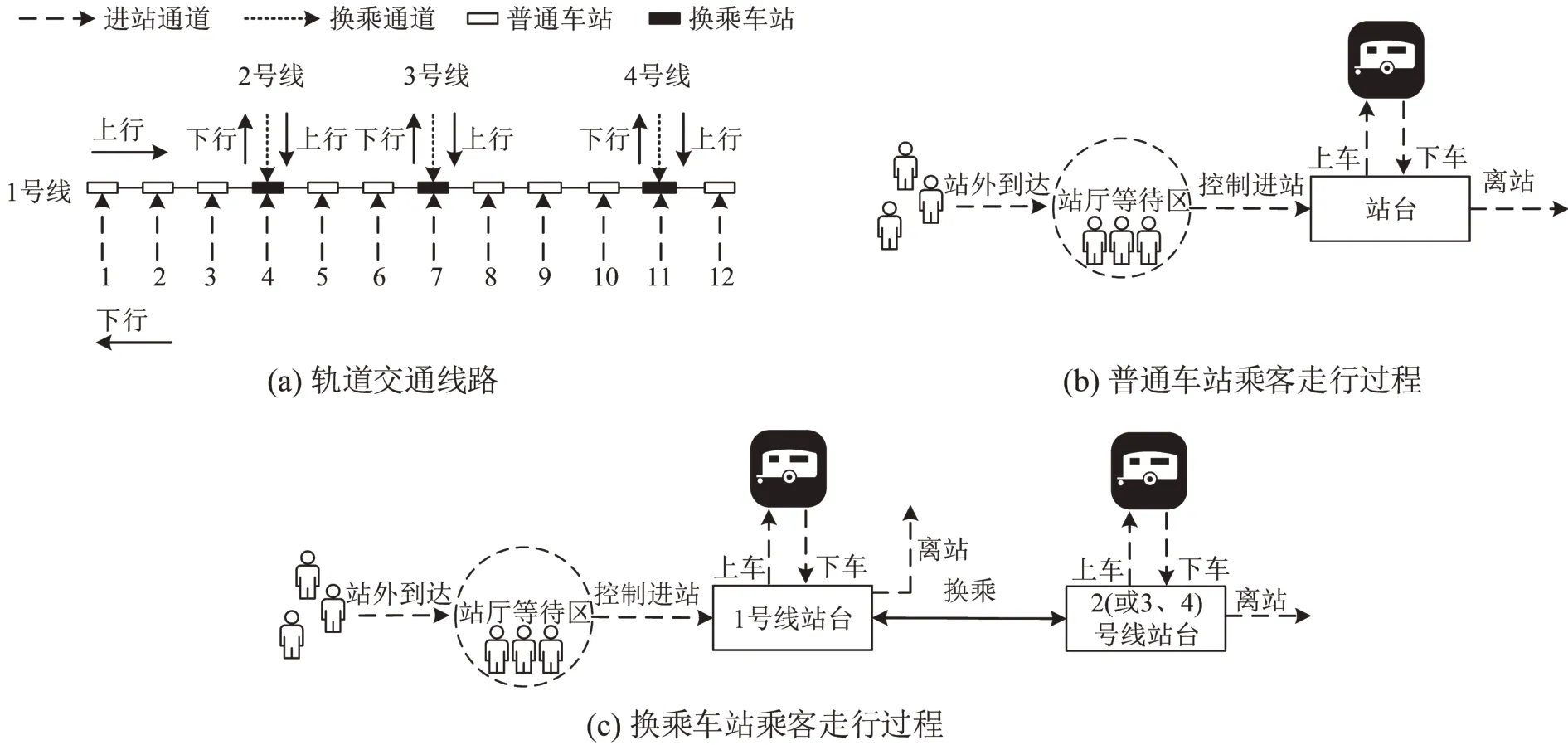
图1 轨道交通线路及乘客走行过程示意图Fig.1 Schematic diagram of rail transit line and process of passengers'travelling

鉴于此，在考虑换入客流影响的基础上，以列车发车间隔、到站、离站时刻和控制进站人数为决策变量，构建城市轨道交通线路列车时刻表与客流控制协同优化模型，以期实现系统优化，缓解全线客流拥挤问题。

2 模型构建

2.1 模型假设及参数定义

模型基本假设如下:

假设1 当车站限流时，已经到达车站的乘客不会选择换乘其他交通工具，即客流需求总量保持不变。

假设2 客流需求及OD 结构已知。在高峰时段出行的乘客大都以通勤为目的，乘客的家庭地址和工作地点相对固定，因此，通过统计分析AFC历史数据，即可获得各车站的客流需求和OD比例。

假设3 除主线路外，其他换乘线路列车时刻表不会发生改变，换入客流到站时刻及OD 结构已知，此外，在实际运营中，高峰期允许短时过载。基于此，假设列车总能力大于换入客流要求。

为便于描述，表1给出本文模型所涉参数及其定义。

表1 变量及参数定义Table 1 Definition of variables and parameters

2.2 约束条件

(1)列车时刻表约束

列车的到发时刻需满足列车运行过程的基本约束，即

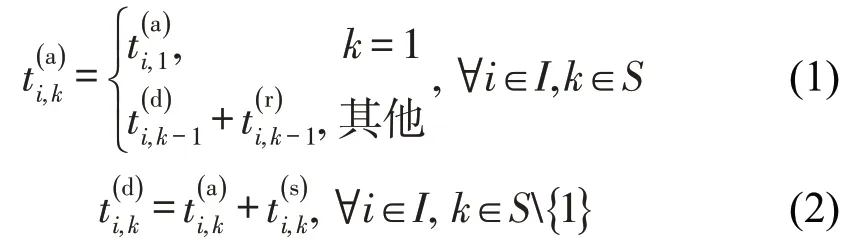
为保证运行安全，列车发车间隔应控制在合理的范围内。由于运行时间和停站时间是固定的，前车i与后车i+1在k车站的发车间隔由列车的离站时刻唯一确定，发车间隔只需在始发站满足上、下限约束，即

(2)客流控制约束

本文假设当车站进行客流控制时，已到达车站站厅的乘客均不会换乘其他交通工具，即所有到站乘客均被服务，计算公式为

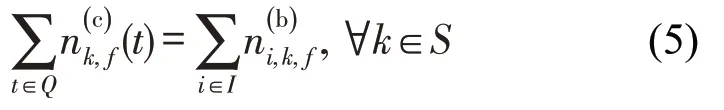
本文假定乘客到达车站后，先在站厅排队等待，因此，当第1辆列车到达车站时，在站厅等待的乘客数量为累积的到达客流量；后续列车到达时，在站厅等待的客流量为累积的到达客流量与累积的已放入客流量之间的差值，且满足非负约束，即

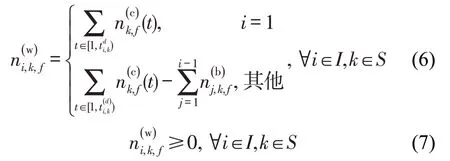
在客流控制策略下，当列车i到达k车站时，允许进站乘客的乘客数量一定小于等于等待的客流量，即

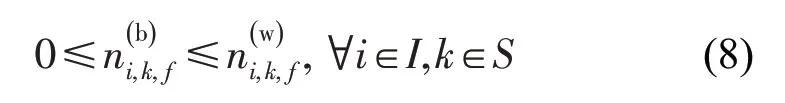
(3)动态载客约束

动态载客过程包含乘客上、下车过程。本文假定任意车站的乘客目的地比例是既定的，则当列车i到达k车站时，下车客流量为以该站为目的地的上游车站的上车乘客总量，即

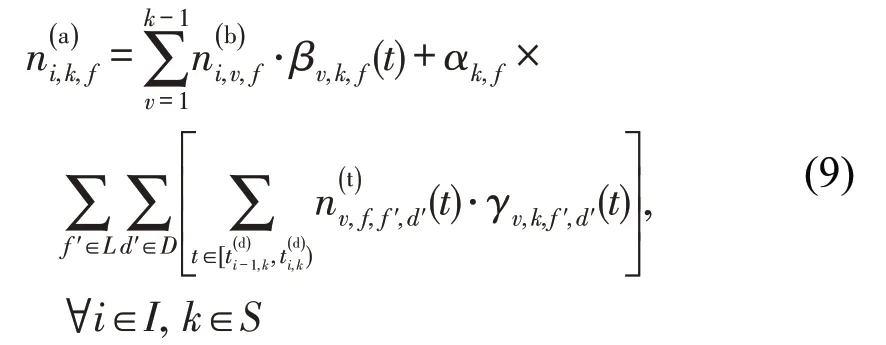
采用客流控制措施的主要目的之一是避免站台客流积累过高，以保证乘客安全。因此，要求控制进站乘客和在站台等待的换入乘客都能够搭乘下一班列车离站。则列车i离开k车站时，车载人数为

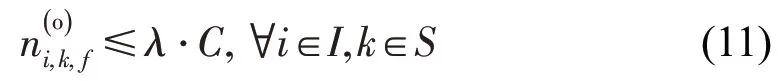
其中，任意时刻t，换乘至主线路k车站的客流量为该车站其他线路换入至该线路方向的客流量之和，即

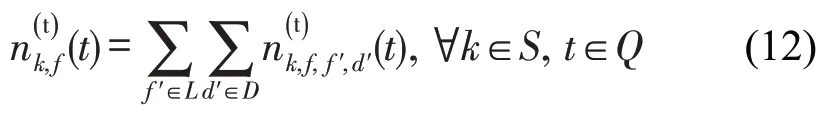
2.3 目标函数

优化目标为沿线所有车站的乘车延误人数加和最少。所谓乘车延误人数，是指受到客流控制措施及列车容量的限制，未能乘坐其到站后到达的首班列车离站，而需在站厅内进行二次等待的乘客人数，即为各列车驶离车站时，所有等待乘客与被服务乘客之间的差值，即

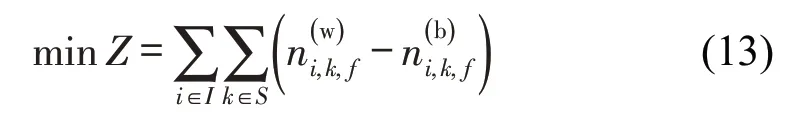
2.4 模型线性化及求解方法

对于∀i∈I,∀k∈S，列车i在车站k的发车时刻为决策变量，因此式(6)，式(9)和式(10)均为非线性约束。为便于求解，引入一组二元变量bi,k（t）|t∈Q，将以上约束进行线性化转换。如图2所示，bi,k（t）=1表示t时刻列车i未到达且未经过k车站，bi,k（t）=0表示t时刻列车i已到达或已经过k车站，因此，该决策变量矩阵为非增矩阵，满足

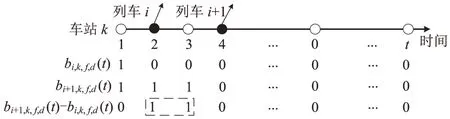
图2 列车运行状态变量Fig.2 Variables related to operating process of trains

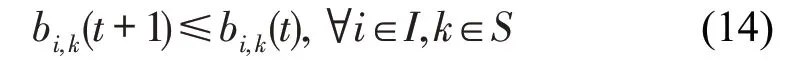
任意两相邻列车的发车间隔为其离开同一车站的时间差，如图2所示，因此，发车间隔需满足

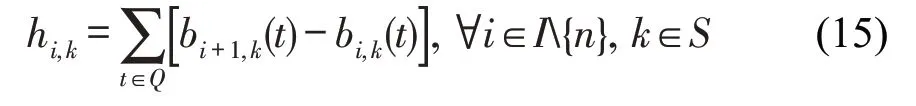
进一步，式(6)可转化为线性约束，即

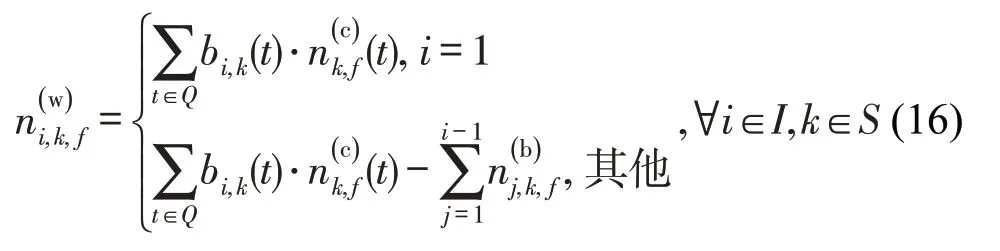
以式(16)中i=1 时为例，在时段t内，若列车1未到达或经过k车站，则bi,k（t）=1，与到达乘客数量相乘即为等待客流量；反之，bi,k（t）=0。将控制时段内所有时间区段的结果进行累加，即可得各车站等待列车1 的客流量。同理，式(9)和式(10)转化为线性约束为

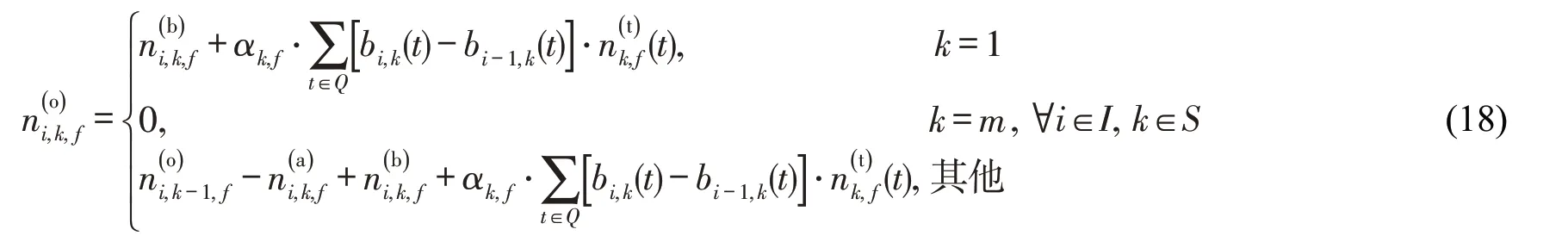
综上，本文所构建的协同优化非线性规划模型转化为标准的整数线性规划模型，可利用优化求解器CPLEX，调用分支定界法对其进行快速求解。

3 实证研究

3.1 基础数据

本文选择某特大城市轨道交通线路为研究对象，通过获取自动售检票系统(AFC)的刷卡数据进行实证分析。如图3所示，该线路连接中心城区与郊区新城，进城方向在早高峰时段通勤客流需求数量庞大且集中，容易造成拥堵，因此，选取该条线路的进城方向进行协同优化研究。使用分支定界法进行求解，并在优化求解器CPLEX 12.6.2 Academic Version上实现，计算的终止条件为上下界Gap为1%。所有实验在CPU为i5-10500-3.10 GHz的Windows10 操作系统上进行。

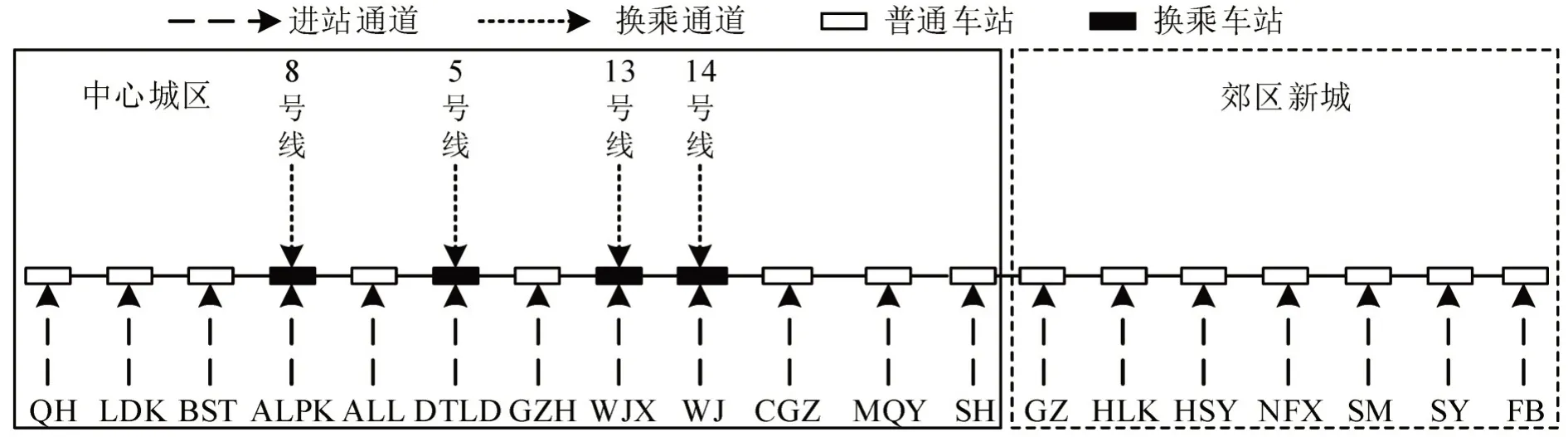
图3 线路示意图Fig.3 Schematic diagram of rail transit line

具体地，选取7:00-10:00 进行研究，首先，将其离散为时间粒度为1 min 的时间区段，则7:00 为第1 个时间区段，10:00 为第180 个时间区段。此外，线路采用单一交路的列车运行模式和“站站停”的停站方案，停站时间作为已知参数给定。模型相关参数如表2所示。

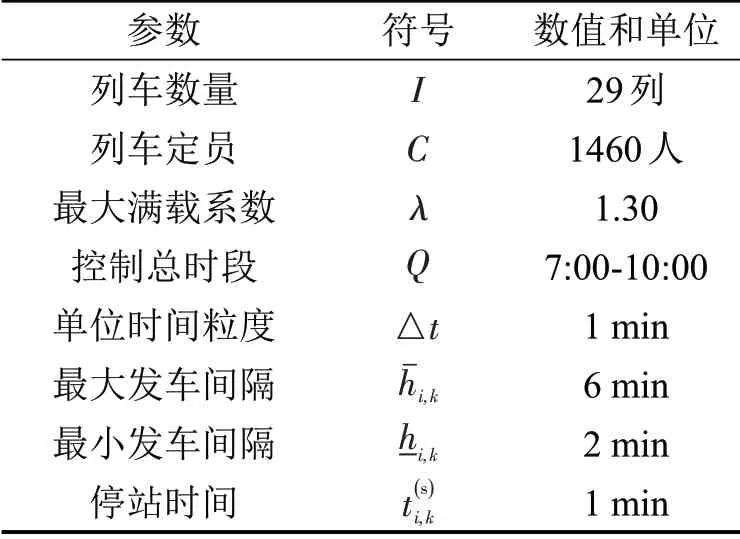
表2 模型相关参数Table 2 Parameters related to model

3.2 结果分析

记本文模型所得方案为方案1，经过62.42 min计算得出Gap 为0.99%的近似最优解，其中乘车延误人数为72607 人，列车运行图如图4(b)所示。可以看出，第1～20 列车的发车间隔较小，均为2，3，4 min，这是因为该时段内客流需求较大，需要匹配相应的运力。

为分析本文协同优化模型的有效性，记优化前的方案为方案2，在该方案中列车时刻表采取实际运营时刻表，如图4(a)所示。进一步，基于方案1，考虑仅面向供给侧，优化列车时刻表以缓解拥堵，即采用方案1所得优化后的列车时刻表，不施加客流控制策略，记为方案3。最后，与大多既有文献一样，在进行协同优化时将第1列车的发车时刻设置为固定值，记为方案4。通过上述实验方案，选取乘车延误人数、乘客平均延误时间和乘客平均等待时间这3个关键性指标，对本文所提方法的有效性进行验证，计算结果如表3所示。

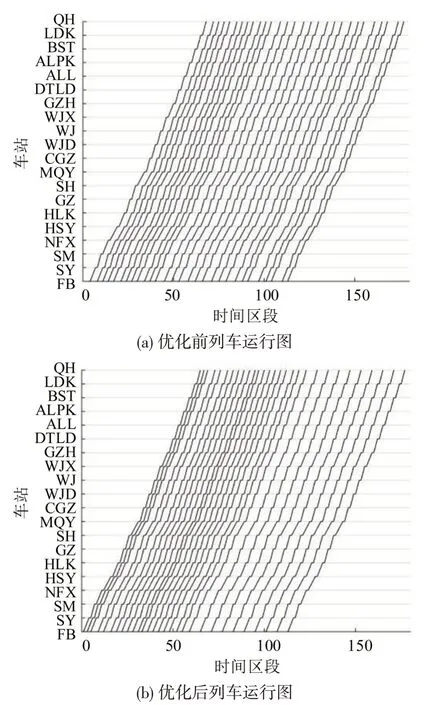
图4 优化前后列车运行图Fig.4 Comparison of train diagrams before and after optimization

表3 各方案结果Table 5 Comparison of experimental results

结果表明，与优化前相比，方案1中乘车延误人数和平均延误时间分别降低28.36%和37.23%；与仅优化时刻表相比，方案1可进一步减少乘车延误人数17.69%，这表明，针对拥堵线路进行列车时刻表与客流控制协同优化是十分有必要的。此外，方案1中乘车延误人数、平均延误时间及平均等待时间均低于方案4，说明面向车流侧和客流侧进行协同优化时，人为地固定某列车的开行计划不足以达到系统最优。图5为上游车站SM 站和下游车站DTLD站的客流聚集情况。可以看出，随列车开行，进行协同优化时，方案1 的客流聚集情况较方案4有所缓解，进一步验证了本文所提方法的有效性。

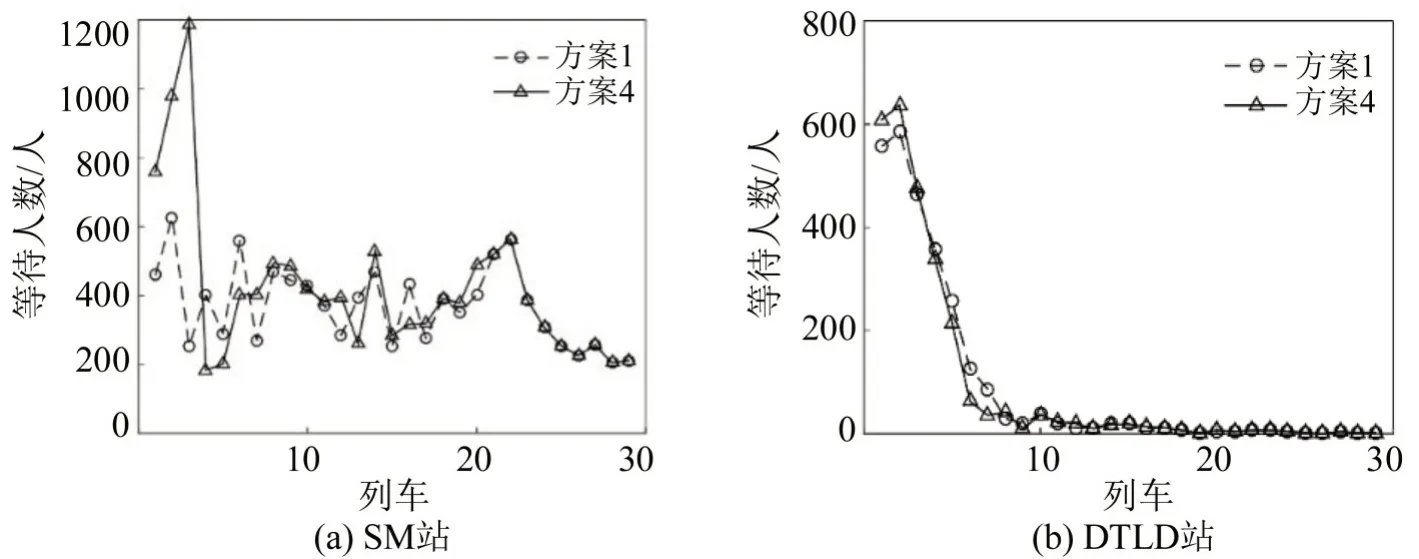
图5 客流聚集情况示意图Fig.5 Comparison of accumulation situations

3.3 灵敏度分析

为探讨最大满载系数对乘车延误人数的影响，对最大满载系数进行灵敏度分析，并记录本文模型(方案1)在不同最大满载系数下的乘车延误人数、乘客平均延误时间、乘客平均等待时间的变化情况，如图6所示。由图6可知，当最大满载系数发生波动时，本文模型均可寻找到近似最优解，具有较好的稳定性；此外，随最大满载系数的增大，上述3个指标均呈递减趋势，这是由于随运力的增加，停站时允许进站乘车的人数会增多，乘车延误人数、乘客平均延误时间、乘客平均等待时间将随之减少。鉴于此，轨道交通运营商可通过增加运力等策略，在保证高服务水平的前提下，提高运力和运量的匹配性从而满足高峰期海量通勤需求。

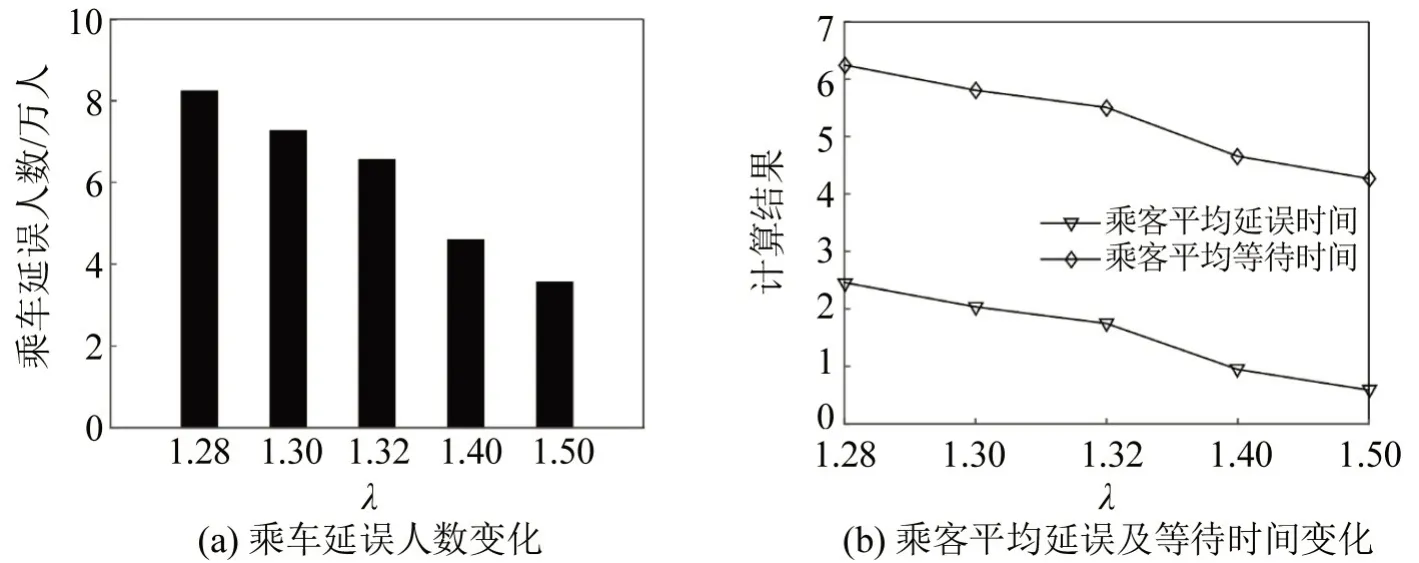
图6 不同最大满载系数下乘车延误人数、乘客平均延误时间、乘客平均等待时间的对比Fig.6 Comparison among various values of λ

4 结论

为缓解城市轨道交通车站拥挤情况，本文提出一种考虑换入客流影响的列车时刻表与客流控制协同优化方法，以最小化乘车延误人数为目标，通过将列车运行过程及乘客出行过程进行耦合并转化为相应的状态约束，构建了协同优化模型。最后将该方法应用于我国某特大城市轨道交通的实证研究中。结果表明：

(1)本文模型对列车时刻表和客流控制进行协同优化，可利用优化求解器CPLEX 调用分支定界法进行快速求解。分析案例发现，本文所提方法与优化前方案相比，轨道交通线路各车站的乘车延误人数、乘客平均延误时间、乘客平均等待时间均显著降低。

(2)本文模型所确定的列车时刻表和客流控制方案在最大满载系数发生波动时具有较好的稳定性，可始终满足约束；乘车延误人数、乘客平均延误时间、乘客平均等待时间均随最大满载系数增大而减小，与实际运营情况相符，验证了本文模型的实用性。