时间阈值对公交不平等评价结果的影响

姚志刚，殷子娟，傅宇豪，汪勇杰

（长安大学，a.运输工程学院；b.交通规划与设计研究所，西安 710064）

0 引言

近年来，公交资源分配不平等问题逐渐受到关注。Delbosc 等[1]较早将可达性与基尼系数相结合进行公交不平等评价。之后这一思路逐渐被接受，即基于公交可达性的基尼系数计算，需要度量获得公交服务或利用公交到达工作岗位或其他社会服务的难易程度[2]。因此，可达性计算的准确性，可能对公交不平等评价结果有重要的影响。然而，可达性研究关注空间因素的影响较多，时间因素仅近年才被提及[3]。用不同时间维度采集的数据会造成可达性计算结果偏差，这种不确定性被称为可变时间单元问题(Modified Temporal Unit Problem，MTUP)，这一问题可进一步分为分割效应(Segmentation Effect)、聚集效应(Aggregation Effect)和边界效应(Boundary Effect)。其中，边界效应被认为是最普遍和影响最明显的可变时间单元问题[3]，它以时间序列起点和终点为边界确定时间阈值，即时间阈值选择问题。

已有文献对计算可达性时的时间阈值选择没有形成共识，通常根据以往研究或调查的经验选定某一时间阈值。Ghorbanzadeh等[4]评价医疗设施可达性时选取30 min作为时间阈值，Hernandez等[5]研究公交的就业可达性时选取40 min 作为时间阈值。而且，可达性比较时所选择的时间阈值也存在差异：Owen 等[6]以10 min 为间隔选取10～60 min 共6 个时间阈值计算就业可达性，发现不同时间阈值下可达性最大值和平均值的空间分布存在差异；Luo 等[7]以5 min 为间隔选取20～50 min 共7 个时间阈值计算医疗设施可达性，发现更大时间阈值下的可达性值的空间分布更均匀；Pereira[8]以30 min 为间隔选取30～120 min的4个时间阈值，比较了快速公交系统可达性的差异，发现不同群体的可达性空间分布因时间阈值不同而差异显著；Guan 等[9]用30 min 和60 min 两个时间阈值计算地铁和出租车两种出行方式的可达性，发现在空间位置影响下两个时间阈值得到的可达性不同，市中心出租车和地铁的POI(Point of Interest)可达性高于城市外围社区的可达性。显然，不同时间阈值下可达性计算结果有差异，且时间阈值选择不一致。

若以可达性为基础数据进行公交不平等评价，需要注意时间阈值对可达性的影响，更应该明确时间阈值对公交不平等评价结果的影响。基于此，本文采用Luo 等[10]改进的两步移动搜索法(E2SFCA)计算学校的公交可达性，并分析不同时间阈值下的可达性分布特征，通过基尼系数及其变化情况比较，探明时间阈值对不平等评价结果的影响，以使公交不平等评价的结论更加科学、可信。

1 研究方法

1.1 公交可达性

公交可达性可以表示乘客利用公交获取社会服务的难易程度，这里表示乘坐公交到达学校的难易程度。可达性高表示公交供给充足，乘客容易获得服务；可达性低表示公交供给缺乏，乘客获得服务困难。这种公交可达性的度量以交通小区质心为中心，以衡量一定服务范围内的教育资源为基础。本文采用两步移动搜索法计算公交可达性，以交通小区质心为需求点度量一定范围内可获得的教育资源数量[7]。这种方法先计算设施周边服务能力与人口数量的比值，然后对需求点的供需比例求和，通常被认为本质上是一种基于重力模型原理的可达性方法。

传统的两步移动搜索法，是用欧几里得距离计算设施周边一定范围内供给的服务与人口的比率。欧几里得距离比真实距离短会导致可达性计算结果偏高，而人口均匀分布假设也受到质疑。考虑距离衰减函数改进的两步移动搜索法，符合学校距离较远时会降低乘客使用公交出行可能性的实际情况，能减少对公交可达性的高估[2,10]。用Luo等[10]的方法计算公交可达性的步骤如下：

首先，将交通小区质心、公交线路、学校位置与站点和路网空间数据相结合，在ArcGIS 10.5 软件中建立网络数据集；选取5 km·h-1作为乘客步行速度计算步行时间和20 km·h-1作为公交运行速度计算公交出行时间，用Network Analyst 工具建立OD成本矩阵，计算各交通小区质心(需求点)与所有公交站点之间的最短步行时间及公交站点与学校(供给点)间最短公交出行时间；输入设定的时间阈值，按最短总出行时间搜索阈值之内的供需点。

其次，以学校j为中心，确定时间阈值t0为搜索半径并形成搜索范围，搜索落在该范围内的所有交通小区k质心，使用距离衰减函数对这些交通小区的人口数量进行加权并求和，再计算学校j的供需比Rj为

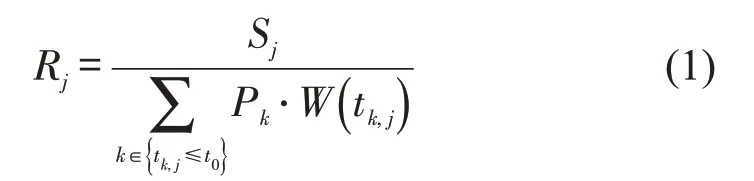
式中：Sj为学校j处的入学人数；t0为给定的时间阈值；Pk为交通小区k的人口数，tk,j为交通小区k的质心与学校j间的总出行时间；W(tk,j)为交通小区k质心与学校j间的距离衰减函数，即高斯函数，计算方法为

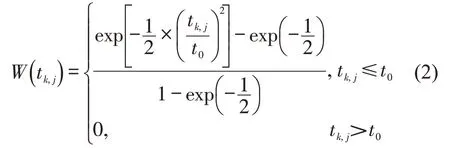
最后，以交通小区k的质心为中心，确定时间阈值t0为搜索半径并形成搜索范围，搜索落在该范围内的所有学校，使用距离衰减函数W(tk,j)对这些学校的供需比进行加权并求和，得到交通小区k的公交可达性Ak为

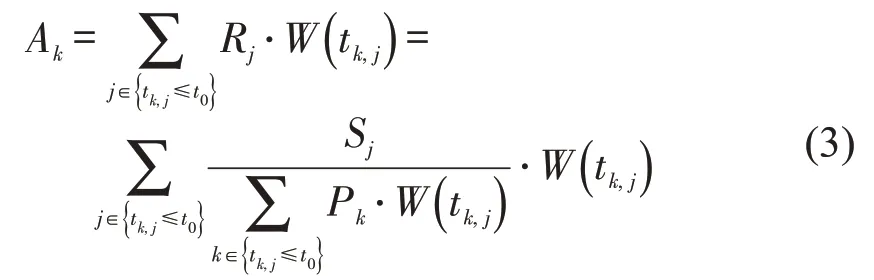
1.2 基尼系数

不平等指数有方差、变异系数、相对平均偏差、对数方差、基尼系数、Theil 指数、Atkinson 指数、Kolm 指数等，其中基尼系数在公交不平等评价中应用最广泛[1]。这里用Delbosc 等[1]的基尼系数计算方法，即

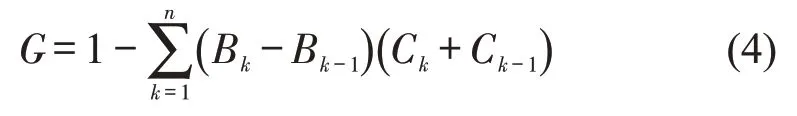
式中：G为基尼系数；Bk为人口累计比例；Ck为公交可达性累积比例(k=0,…,n，且B0=C0=0,Bn=Cn=1)；n为交通小区个数。

基尼系数取值为0～1，取0 表示各交通小区之间的公交服务完全平等，取1表示完全不平等。相应地，基尼系数越小表示公交资源分配越平等，基尼系数越大表明公交资源分配越不平等。表1为不同区间基尼系数所代表的公平情况[11]。

表1 联合国基尼系数评价标准Table 1 Gini coefficient evaluation criteria of United Nations

除作为衡量公交总体不平等指数之外，基尼系数还可以进行子群分解，将总体不平等分解为子群内部和子群之间不平等两部分，由于Dagum[12]提出的基尼系数分解方法需考虑子群之间的重叠，因此要增加交叉项来反映子群之间的重叠程度。这一可分解特性可用来研究公交不平等的构成与来源。

2 调查与数据

2.1 调查区域与数据来源

本文以浙江省海宁市为研究对象。海宁市位于浙江省东北部，东邻海盐县、南濒钱塘江、西接杭州市、北连桐乡市，下辖4 个街道、8 个镇，共225 个行政村(社区)。截至2017年12月，海宁市有公交线路104条，站点1164处，运营车辆487台，年客运量3468 万人次。根据海宁市公交线路、站点及各镇(街道)的行政区划，利用ArcGIS 10.5软件建立矢量化数据库，得到如图1所示的公交线网与站点空间分布，公交系统基本情况如表2所示。

英格曼一下推开了厨房的门。他脑子里只剩一闪念：但愿这些女人能像所有的中国良家女子一样，温顺地接受自己的命运。

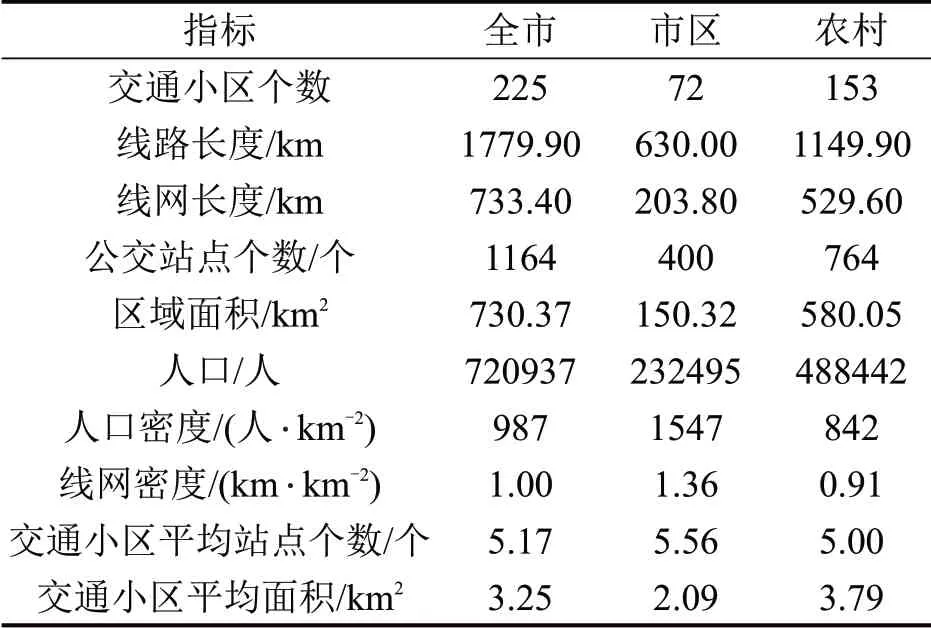
表2 海宁市公交系统基本信息Table 2 Basic information of public transport system

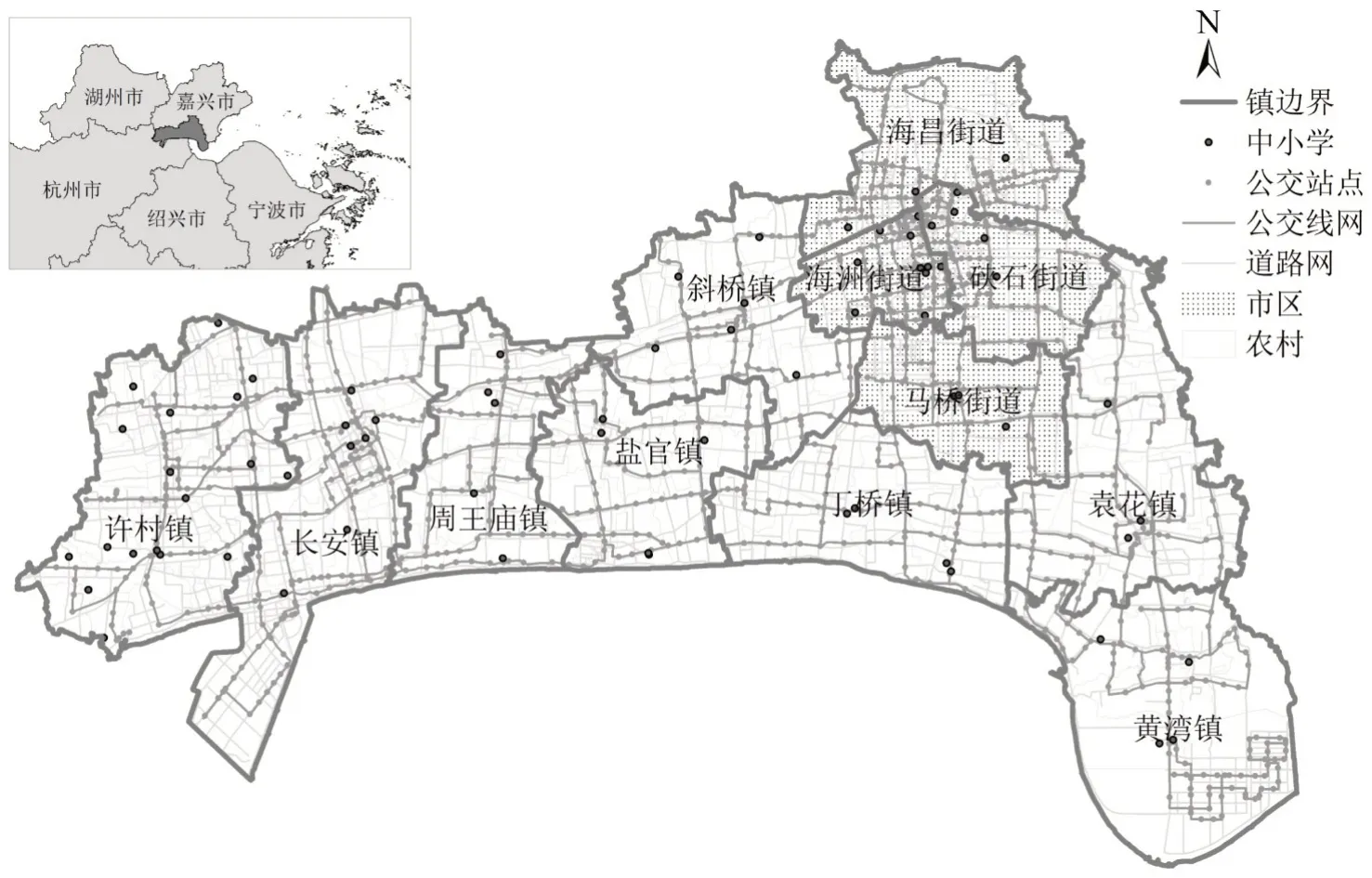
图1 公交线网布局与行政区划Fig.1 Public transport network and zonal districts

为了便于对比，参考《海宁市城市总体规划》《海宁市城镇体系规划》，将构成海宁市中心城区的海洲、硖石、海昌和马桥4 个街道的行政管辖范围视作市区，将许村、长安、周王庙、盐官、斜桥、丁桥、袁花和黄湾8 个镇的行政管辖范围视作农村。选取74所中小学校，其中小学46所、初中22所、高中6 所，学校名称和学生数量等信息来源于海宁市教育部门2013年统计资料，学校位置来自于高德地图POI数据。

2.2 不同时间阈值的可达性分布特征

实际获取到的数据中只有公交乘客的上车站点信息，通过VBA 编程对乘客支付信息与车辆运行数据进行匹配，推算出乘客下车站点及其时间，得到不同出行时耗的乘客数量分布如图2所示。可以看出，海宁市公交出行时耗2 min 以上乘客的数量持续减少，且出行时耗10 min以内的乘客占总数的48.08%，30 min 以内的占82.99%，超过30 min的占17.01%。由于99.08%公交乘客的出行时耗在90 min 以内，参照Owen 等[6]的做法，以10 min 为间隔，选取10～90 min共9个时间阈值进行研究。

图2 公交乘客出行时耗Fig.2 Public transport passenger travel time

根据式(3)得到各时间阈值下的公交可达性，借助ArcGIS 10.5软件用自然间断分类法将公交可达性分为“非常高”(0.08, +∞)、“很高”(0.07, 0.08]、“高”(0.06, 0.07]、“较高”(0.05, 0.06]、“中等”(0.04,0.05]、“较低”(0.03, 0.04]、“低”(0.02, 0.03]、“很低”(0.01,0.02]、“非常低”[0.00,0.01]共9 个相对等级，总体、市区和农村这3个空间范围按时间阈值统计的公交可达性数量分布如图3所示。

从图3可以看出：市区和农村交通小区低等级公交可达性所占比例(6.94%～77.12%)，明显高于高等级公交可达性所占的比例(0～18.06%)；而且，随时间阈值的增加，公交可达性“非常高”“很高”“非常低”这3个等级所占比例逐渐减少，其他6个等级所占比例逐渐增加，但仅有“低”等级是一直增加；不同时间阈值下，农村的公交可达性以“非常低”“很低”这2 个等级为主，占农村交通小区数量的52.29%～77.12%，而市区各等级公交可达性的分布比农村均匀；同时，由于农村交通小区的数量远远高于市区，使得全市各等级公交可达性随时间阈值的变化特征与农村基本一致。

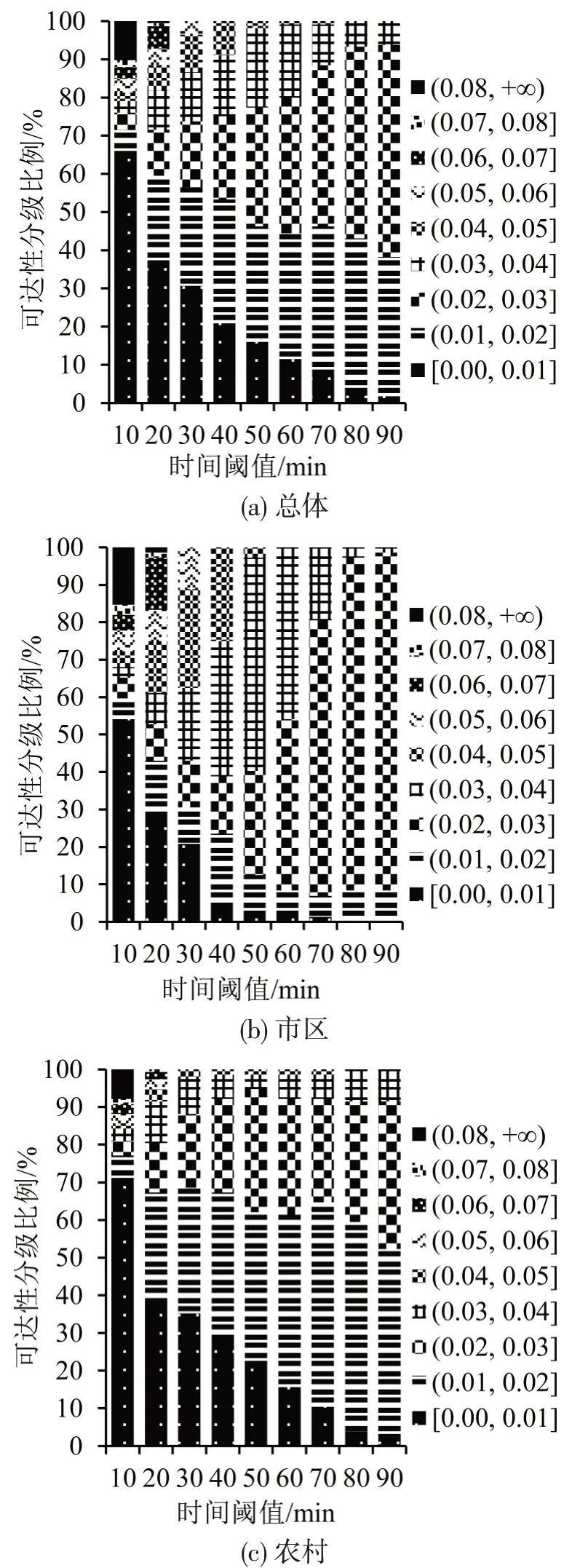
图3 公交可达性等级分布比例Fig.3 Percentage distribution of public transport accessibility levels in three regions

图4为9 个时间阈值下的公交可达性空间分布。时间阈值较小时，如图4(a)～(c)所示，市区的公交可达性明显高于农村，表明市区公交资源供给水平高、出行便利。在10 min 时间阈值下：市区中心城区外围有33 个交通小区的公交可达性为0，其中，海昌街道13 个、马桥街道7 个、硖石街道9 个、海洲街道4个；农村有98个交通小区的公交可达性为0，其中许村16 个、长安15 个、丁桥和盐官各14个、袁花13 个、周王庙12 个、斜桥8 个、黄湾6 个。在20 min 时间阈值下：市区的海昌街道有4 个、硖石街道有2 个交通小区公交可达性为0；农村有19个交通小区的公交可达性为0，其中，袁花和长安各4个、丁桥和许村各3个、斜桥和周王庙各2个、盐官1 个，表明这些区域公交资源供给水平低、出行不便。时间阈值较大时，如图4(g)～(i)所示，市区的公交可达性依然比农村高，但两个区域差异减小。此时，市区边缘的新塘、民胜、利众、杨汇桥、永丰、军民、双合等区域公交可达性不高，农村的辛江(长安镇)以及河东街社区(袁花镇)公交可达性明显降低。总体上看，随时间阈值增大公交可达性的空间分布趋于均匀，市区与农村的公交可达性区域性差异变小。

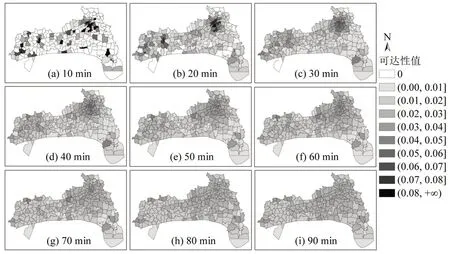
图4 不同时间阈值下的公交可达性空间分布Fig.4 Public transport accessibility with multiple time thresholds

3 结果分析与讨论

3.1 基尼系数比较

在各时间阈值下所计算的可达性值的基础上，用式(4)计算研究区域总体、市区和农村这3个空间范围公交服务的基尼系数，结果如表3所示。总体上看，不同时间阈值下基尼系数差异较大，选择不同时间阈值所得公交不平等评价结果差异明显，即参照表1以10 min为时间阈值，会得到研究区域公交服务“差距悬殊”（G≥0.5）的评价结论；而以90 min 为时间阈值，则会得到“比较平均”或“相对合理”（0.2 ≤G＜0.4）的评价结论。

而且，基尼系数随时间阈值增大而减小，总体基尼系数最高值0.842、最低值0.309，最高值与最低值的比值为2.73；市区基尼系数最高值0.729、最低值0.295，最高值与最低值的比值为2.47；农村基尼系数最高值0.893、最低值0.310，最高值与最低值的比值为2.88。这一结果表明，农村基尼系数受时间阈值影响最大，其次为总体，市区基尼系数受时间阈值的影响最小。

进一步，对比表3中同一时间阈值下的基尼系数，可以发现，各时间阈值下市区的基尼系数均低于农村，但总体与农村基尼系数之间的差异因时间阈值而不同：时间阈值在10，20，90 min 时的总体基尼系数低于农村基尼系数，但时间阈值在30～80 min之间时的总体基尼系数高于农村基尼系数。

表3中基尼系数呈连续下降趋势，表明选择越大时间阈值，会使研究区域公交不平等评价结果越公平。基尼系数下降趋势先快后慢，表明公交不平等评价结果受时间阈值影响的幅度递减。

表3 不同时间阈值下的基尼系数Table 3 Gini coefficients at three spatial scales with time thresholds

而且，市区和农村基尼系数随时间阈值增大而减小的趋势基本一致，但总体基尼系数变化却不同。时间阈值大于30 min时，总体基尼系数的减小幅度，明显小于市区和农村基尼系数的减小幅度，时间阈值大于60 min时则相反。

3.2 时间阈值影响的城乡差异

由于不同时间阈值下市区和农村基尼系数的变化，无法对总体基尼系数趋缓更明显的现象做出解释。这里考虑区分市区和农村两个群组，对总体基尼系数进行分解，以分析总体基尼系数变化的原因。于是，采用Dagum[12]的方法进行总体基尼系数分解，得到表4所示结果。

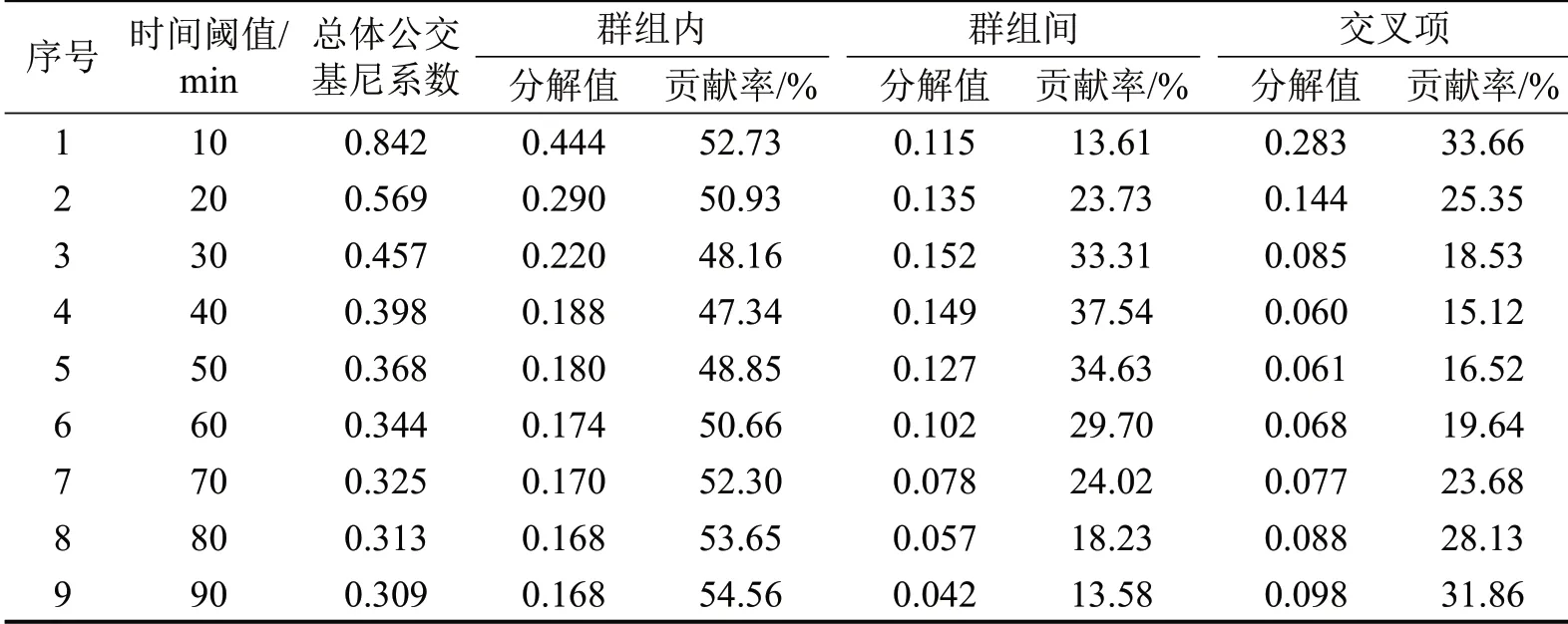
表4 总体基尼系数分解结果Table 4 Decomposition of total Gini coefficients

基尼系数分解将全市总体公交不平等分为市区和农村两个群组内部的不平等和两个群组之间的不平等两部分，分别计算出群组内和群组间的公交不平等对全市总体公交不平等的贡献率，进而为总体公交不平等的改善指明方向。此外，分解结果还存在交叉项，但由于目前对基尼系数分解后的交叉项无法给出一致性解释，故这里将其忽略不做分析。

从表4中公交不平等贡献率变化看：市区与农村两个群组内部的公交不平等对全市总体公交不平等的贡献率，随时间阈值增大先减小后增大；而市区与农村两个群组之间的公交不平等对全市总体公交不平等的贡献率，则随时间阈值增大先增大后减小。可以发现，两个群组内部与群组之间公交不平等对总体公交不平等的贡献率相反的变化趋势更加明显。同时可以看出：群组内的贡献率在40 min 时间阈值下为最小值，之后逐渐增大；群组间的贡献率在40 min时间阈值下为最大值，之后逐渐减小。在每个时间阈值下，两个群组内部不平等对总体公交不平等的贡献率大于群组之间不平等的贡献率。而且，随着时间阈值变大，市区与农村群组内部的公交不平等的贡献率先减小后增大。

以表4中分解值变化为基础，结合图5不同时间阈值下的基尼系数分解值变化量，就容易解释表3总体基尼系数随时间阈值变大而缓慢递减的现象。表4显示市区与农村两个群组内的不平等成为造成全市公交不平等的主要来源，群组内分解值随时间阈值的增加而减小，但其对总体不公平的贡献率先下降后上升；群组间分解值在10～30 min时随时间阈值增加而增加，40～90 min 时随时间阈值增加而减小，而贡献率呈先增长后下降趋势。这一结果，受交叉项分解值及其对总体不平等贡献率变化的影响，但因基尼系数交叉项解释尚存在争议而对此不展开阐述。

从图5可以看出，随着时间阈值增加，分解结果中组内不平等减小的幅度逐渐减小，由于其他两个组变化趋势相反，在40～90 min 时群组间不平等随时间阈值的增加而减小的幅度小于交叉项在10～40 min减小幅度，故总体上随时间阈值增加使总体基尼系数减小幅度降低。因此，以表3中市区与农村基尼系数为基础，结合总体基尼系数分解结果，才能将时间阈值对公交不平等评价结果的影响分析得更加深入，这也体现出进行基尼系数分解的必要性。

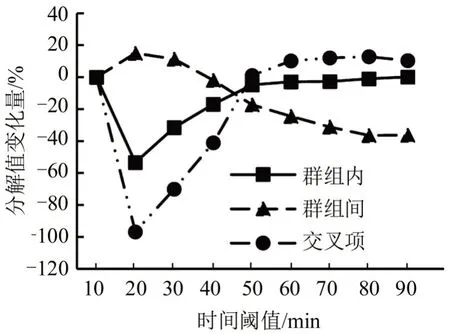
图5 总体基尼系数分解值变化量Fig.5 Variations of decompositions of the total Gini coefficients

4 结论

用Luo 等[10]改进的两步移动搜索法计算学校的公交可达性，分别分析了不同时间阈值下公交可达性分布和基尼系数的差异，从市区和农村两个空间群组对全市总体基尼系数进行分解，进一步分析时间阈值对公交不平等评价结果的影响，得出以下两个结论：

(1)不同时间阈值下的基尼系数存在明显差异，随着时间阈值增大，全市、市区和农村这3个空间范围的公交不平等评价结果从“差距悬殊”变为“相对合理”，使用不同时间阈值进行公交不平等评价会出现结果偏差甚至得到相反的结论。

(2)时间阈值对研究区域总体公交不平等主要来源的大小的判定有影响，总体公交不平等的主要来源为组内不平等且随着时间阈值增大由逐渐下降变为逐渐上升，使用不同时间阈值进行总体公交不平等来源判定会出现结果偏差。因此，应在公交不平等评价时谨慎选择时间阈值。

需要指出的是，已有文献对两步移动搜索法的改进主要针对时间阈值和距离衰减函数的选择，可以构建服务供给能力表达式或选择更符合实际的距离衰减函数进一步改进两步移动搜索法，以使公交可达性计算更加合理。另外，这里仅计算了市区和农村两个空间群组的基尼系数并从这两个群组角度进行总体基尼系数的分解，待数据条件满足后应从不同年龄或考虑弱势群体等角度进行乘客群组划分，以使研究成果更具有实践价值。