基于乘客感知的多模式公交服务质量差异性研究

朱兴林，姚亮，刘泓君，叶拉森·库肯，克然木·司马义

（新疆农业大学，交通与物流工程学院，乌鲁木齐 830052）

0 引言

城市公交客运是居民正常出行的基本保障，具有能耗低、运量大、效率高等优势[1]。随着快速公交、定制公交等交通基础设施的建设，我国城市公交客运系统逐步向多模式公交网络方向发展。与单一模式公交网络不同，多模式公交的协调运转，可以在某类公交服务能力不足时，通过转接、换乘等方式将交通需求分散至公交运营网络中，提升公共交通系统的运输能效。现阶段，国内外学者针对多模式公交的研究，主要集中于线网规划[2]及运营模式[3]方面，针对服务质量综合评价的研究相对较少，不同公交方式间服务质量存在的差异可直接或间接影响乘客的出行选择，从而对整体公交系统运输效率产生影响。因此，基于乘客感知评价分析多模式公交的服务质量及其差异性，有助于辨识各模式公交在运营、服务方面存在的短板，有针对性的提升公交吸引力及公共交通系统的服务水平[4]。

服务质量客观反应了乘客对公交发展水平及服务能力的感知，因服务质量具有无形性，CHENG等[5]从乘客感知角度出发，以满意度为服务质量的衡量标准，发现满意度的提升可促使居民乘坐公共交通出行。从研究方法角度看，针对城市公交服务质量的研究多数运用Logit、Multinominal Logit 和Probit 等非集计模型，可以分析选取指标的影响能力，不少学者使用模糊集理论、灰色理论等方法探索服务质量的影响因素，但在分析时难以捕捉不同维度指标间的潜在影响关系。但基于概率论与因子图的贝叶斯网络(Bayesian Network)与大部分模型不同，可以针对不确定性因素，通过结构学习挖掘出影响因素间的潜在规则[6]，吴静娴等[7]采用贝叶斯网络建立城市常规公交乘客满意度分析模型，推理得出乘客满意度的交互影响关系及指标影响力，验证了贝叶斯网络的分类准确度。也有学者在评价公交服务质量时使用神经网络、决策树等数据挖掘算法，通过分类识别探究公交服务质量的影响因素。从评价角度看，常规的公交服务质量评价多以定性、定量分析为主，前者针对影响关系及能力进行深入研究，后者多以较常规的离散、回归分析为代表，探究因变量与自变量之间的影响强度，两者在分析过程上有着明显的差别[8]。

现有研究中，面向常规公交的服务质量评价研究，已积累了丰富的经验及成果，但研究多数针对某种特定的交通方式进行分析，对多模式公交服务质量的差异性研究相对较少；另一方面，针对公交服务质量影响因素的分析多基于单一时间截面数据，结合时间维度的变化特征，组合使用多种方法对服务质量进行评价及优化效果预测检验的研究还有待补充。因此，本文从公交方式、时间两个截面入手，采用TAN 贝叶斯网络与IPA 分析，评价多模式公交服务质量；选取LSTM、MLP、SVM进行多方法对比，选取最优预测方法，对评价结果进行检验及敏感性分析，以多方法组合的形式辨识多模式公交服务质量的差异性，并提出相应优化方案。

1 数据调查与分析方法

本文以新疆某市为研究区域，将乘客满意度作为公交服务质量的衡量标准，针对市区线路、郊区线路、快速公交和定制公交线路共145条线路进行了满意度问卷调查。为追踪、总结多模式公交服务质量的变化情况，降低样本容量为数据分析带来的真实性偏差，于2015年12月—2018年12月开展持续性调查，收集各模式公交问卷44500 份，剔除无效问卷后收回43610份问卷，有效率为98%。

对问卷进行信度、效度检验，信度检验采用克朗巴赫α信度系数法(Cronbach's Alpha)；效度检验采用KMO 检验和Bartlett 球体检验，结果如表1所示。结果表明：4种公交方式Cronbach's Alpha系数均大于0.7，问卷可靠性良好；KMO 值均符合大于0.6的要求，Bartlett球体检验结果显著，说明问卷结构效度较好，适合进行数据分析。

表1 问卷信度、效度分析结果Table 1 Results of questionnaire reliability and validity analysis

调查问卷主要采用Likert 5 级量表法，由乘客对公交服务进行认同性评价，除总结相关文献对各模式公交服务质量评价指标的选用外，问卷还考虑了研究区域的公共交通发展水平、企业经营情况和气候等因素，并对服务质量评价指标维度进行重新划分，根据实际交通条件调整各维度的指标选定，问卷设计如表2所示。

表2 问卷设计Table 2 Questionnaire design

本文需解决以下问题：

(1)辨识各模式公交服务质量存在的差异，找出需要优化改善的主要指标；

(2)多模式公交有众多影响因素，如何针对不同公共交通方式确定各指标优化的次序；

(3)若依据评价结果进行优化，是否有助于提升服务质量。

针对上述问题，本文采用TAN 贝叶斯网络，基于公交方式截面进行结构学习，推理得出各维度指标对乘客满意度的综合影响力及潜在影响规则；基于时间截面，结合指标影响能力及乘客满意度均值，引入IPA 分析方法，识别各公交方式服务质量的主要影响因素；最后，选取MLP、LSTM神经网络与SVM 分别建立回归预测模型，选取预测效果最佳的方法预测乘客满意度发展趋势，并针对各模式公交需优化的主要指标进行敏感性分析，参照影响因素的潜在联系提出优化方案。研究技术路线如图1所示。

图1 研究技术路线Fig.1 Technical route of research

2 城市多模式公交服务质量评价

2.1 贝叶斯网络原理

贝叶斯网络(Bayesian Network, BN)是一种基于概率论和因子图的不确定信息推理模型，以朴素贝叶斯网络为基础的树形增强朴素(Tree Augmented Native,TAN)贝叶斯网络可以允许预测的每个变量除关联目标变量外，还依赖其他预测变量，有效增加了贝叶斯分类器的准确程度[9]。TAN贝叶斯网络中的联合概率分布为

式中：属性变量Xi的父节点π(Xi)除了包含类变量Y，还包含其他属性变量。

TAN 贝叶斯网络是由节点与有向边组成的有向无环因子图，网络中的节点由属性变量X和类变量Y组成，有向边表示各变量间的概率依存关系，如图2所示。

图2 TAN贝叶斯网络结构Fig.2 Structure of Tree Augmented Native Bayesian network

在判断变量节点间的关系时，贝叶斯网络是通过对节点Xi与Xj之间的互信息I(Xi,Xj)进行结构学习，确定因素间的关联性，即

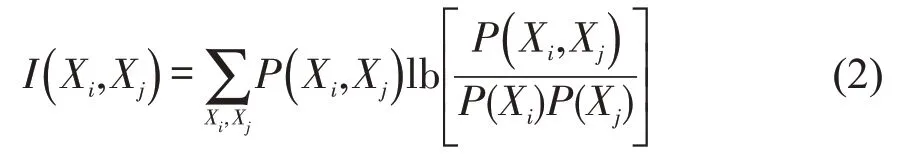
TAN 贝叶斯网络使用最大加权生成树构建属性网络，计算节点间的互信息，根据互信息产生影响关系和权重，遵循已选边不组成回路的原则，构建最大权重生成树。对朴素贝叶斯网络进行树形增强，能够有效提高贝叶斯分类器的精度，准确地得出变量间影响关系及权重值。

2.2 基于公交方式截面的服务质量影响因素分析

采用TAN 贝叶斯网络，针对市区线路、郊区线路、快速公交和定制公交的问卷数据，分别进行互信息值运算及结构学习，将乘客满意度设为反映服务质量的类变量，其余维度指标作为属性变量，互信息值运算过程为

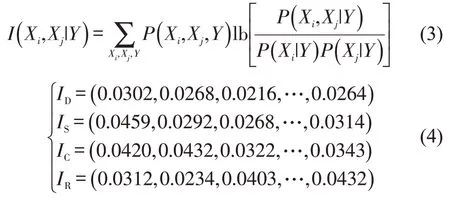
式中：I(Xi,Xj|Y),i=1,…,n,j=1,…,n,i≠j，Xi与Xj为已知属性变量，Y为Xi与Xj的共同父节点，计算得到各类型公交每个选取指标与乘客满意度影响能力权重值；ID、IS、IC、IR分别为市区线路、郊区线路、定制公交、快速公交的I值。推理过程将需要求解的节点集设为Q，已定值变量的集设为F，m为样本总量，根据贝叶斯定理可知

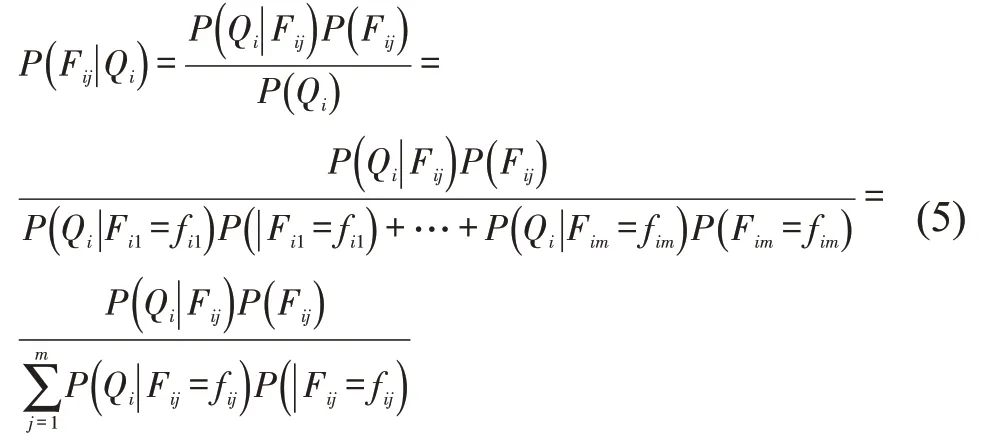
由式(5)得出各节点间相互关联的条件概率，并根据互信息值与TAN贝叶斯网络结构学习，得出4种公交方式的服务质量影响关系网络，如图3所示。

图3中，4 种公交模式的服务质量网络结构存在显著差异，但便利性指标间均有逻辑性关联。线路及站点的合理设置（A6）有助于提升乘客对乘车时长（A1）、换乘便利性（A5）和到站步行时间（A2）的感知；支付的便捷性（A7）可以通过影响乘客排队上车时间对候车时间（A3）及乘车时长（A1）产生影响。除此之外，TAN 贝叶斯网络还通过概率推理，得到不同维度指标间存在的非逻辑性潜在相关，例如，在快速公交网络中，若以消防设施（B4）为优化目标，应考虑与其关联的服务人员规范程度（C3）和站点安全设施（E4），从运营管理的角度提出相应优化方案，由此可知，服务质量影响关系网络可为制定服务质量优化方案提供参考。

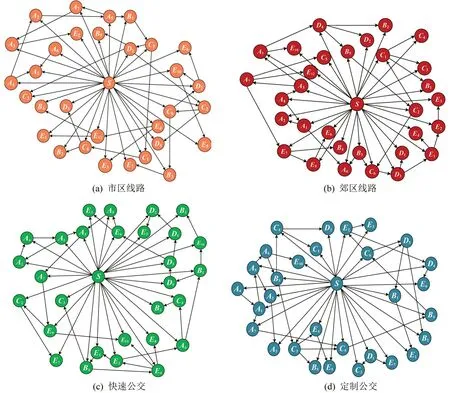
图3 服务质量影响关系网络Fig.3 Network of relationships influencing service quality

采用最大似然法检验运算过程，得出市区线路、郊区线路、快速公交和定制公交模型总体正确率分别为：87.06%、81.32%、85.82%和82.22%，拟合程度较好。对结果进行分析，影响因素权重值如表3所示。

表3 影响因素权重Table 3 Weight of influence factors

从影响能力角度看，表3中市区线路E5、E6、E7、E10，郊区线路A1、B1、E7，定制公交B2、C3、C6、E5，快速公交A3、A7、E4、E6、E9指标的优化均可通过提升乘客总体满意度提升各交通方式服务质量。但识别主要优化指标时，应考虑4年中各指标平均满意度的变化情况，综合评价各指标服务水平，考虑是否需要对其进行优化调整。

2.3 基于时间截面的公交服务质量评价

为综合评价城市公共交通服务质量，在TAN贝叶斯网络基础上引入重要性绩效分析(Importance Performance Analysis, IPA)，将指标影响能力和满意度作为参数，以四分图的形式评价选取指标的服务水平，总结指标在所有时间截面出现的频率，对IP 值进行计算与排序，识别影响各模式公交服务质量的主要因素。针对每个时间截面数据，将TAN 贝叶斯网络得出的指标影响能力权重作为横轴数据源，纵轴为各指标满意度归一化值，进行服务水平定位分析。2015年4 种公交方式的IPA定位分析结果如图4所示。

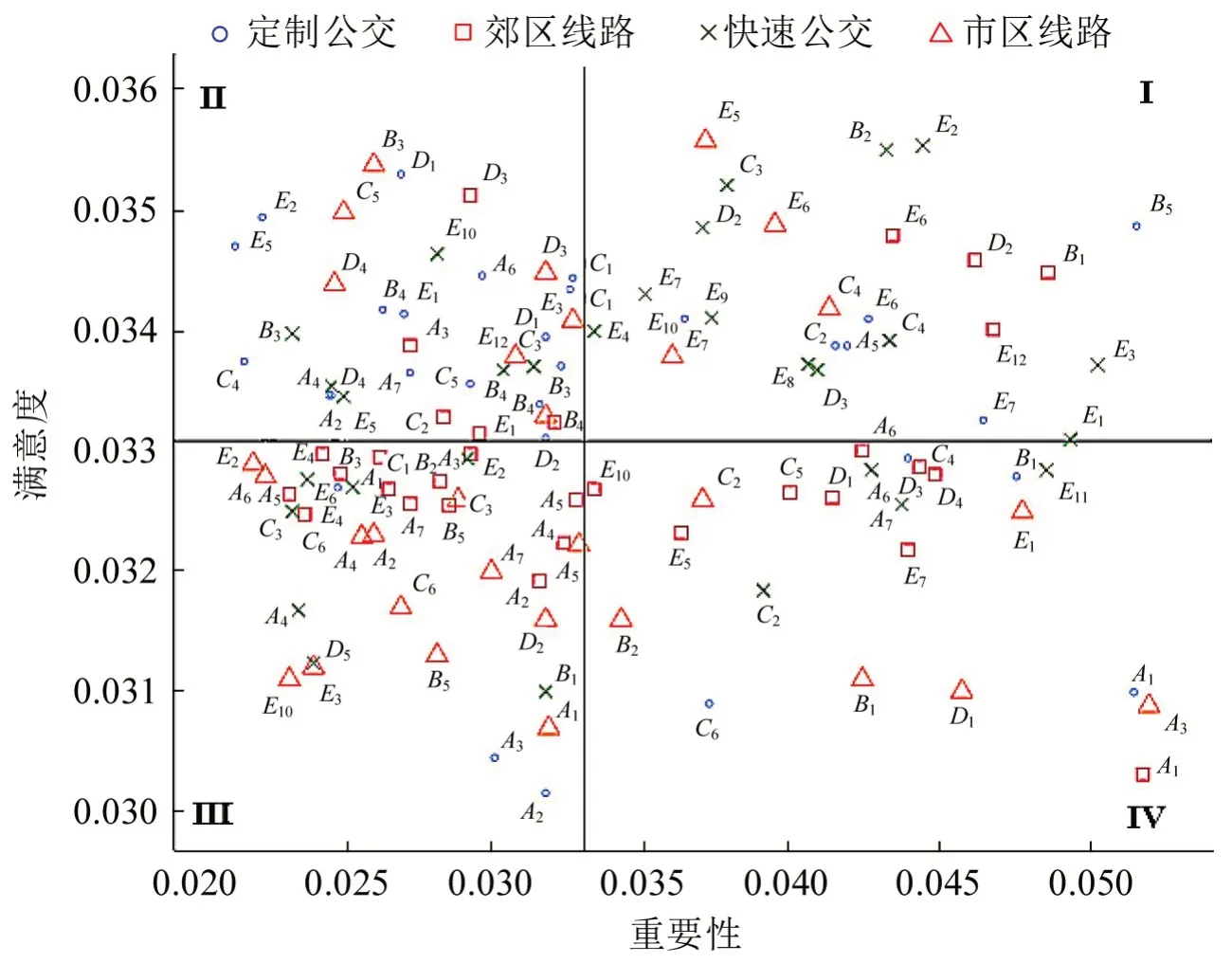
图4 IPA定位分析Fig.4 Importance-Performance Analysis grid

图4中，根据指标重要性、满意度与坐标轴的距离，确定象限Ⅰ为发展优势区；象限Ⅱ为继续保持区；象限Ⅲ为次要发展区；象限Ⅳ是重点改善区，重要性高且满意程度较低，需要重点提升服务水平。依次对4个时间截面的各模式公交进行IPA定位分析，总结位于象限Ⅳ的指标，如表4所示。

表4 重点改善指标Table 4 Indicators of key improvement

由表4可知，定制公交与快速公交位于象限Ⅳ的指标数量相对小于市区和郊区线路，且在4个时间截面中指标的变化浮动较小。从规划角度考虑，定制公交客流量较小，且使用者相对固定，因此，在城市公交整体线路动态调整及需求调查时易遭冷落。快速公交有单独的线路、车辆及站点设施，与常规公交运行模式有所差异，除其自身独有的E9和E11服务水平较低外，还与其他公交方式一样有B1、C2和E10需要重点改进。市区线路与郊区线路需要重点改善的指标较多，且浮动性较强，因此，需要进一步的量化分析找出主要影响因素。总结表4中各公交方式指标及出现的频率，并对IP值进行运算及排序，即

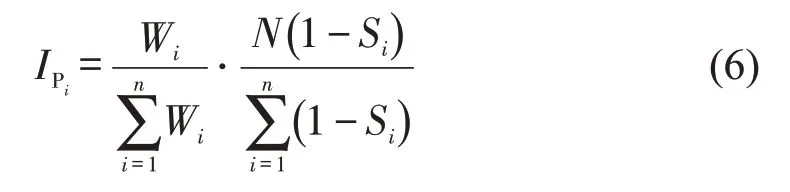
式中：IPi为第i个重点改善指标的综合评价指数；Si为第i个重点改善指标的平均满意度；Wi为第i个指标的重要度值；N为该指标在表4中出现的频率数；n为重点改善指标总数。由式(6)可知各指标的综合评价指数不仅考虑综合权重，还考虑指标的不满意度，并引入频率数及不满意度归一化值，消除了指标数量不一致带来的权重偏差和量纲的影响，重点改善指标IP值结果如表5所示。

表5 影响因素IP值对比Table 5 Comparison of IP values of influencing factors

表5中逆序为指标按照IP值大小排列的位置，数值越低表示该指标越需改进。因各公交方式重点改善指标数较多，IP 值的值域为0.0003～0.0034，以IP值大于等于0.0010为标准，则4种交通方式共18 个指标为当前多模式公交服务质量的主要影响因素。

对于市区线路，需要提升服务水平的指标主要有：A3、B1、B2、C2、E6和E10；郊区路线乘客满意度的主要影响因素为：A1、A3、C4、E5、E7和E10；快速公交当前阶段主要问题在于：B1、C2和E10；影响定制公交服务质量的因素较少但是逆序靠前，有A1、B2和E10。4 种公交方式的乘客均认为在乘车时存在着车厢拥挤（E10）状况，该指标在定制公交及快速公交的平均满意度均为0.68，远低于其他影响因素。市区线路与快速公交均存在着车速不稳定（B1）的问题，且根据满意度与IP值，市区线路在该问题上较严重。从评价结果来看，上述指标均处于服务水平较低的状态，对指标进行优化，为整体公交服务质量带来的提升效果还需进一步检验分析。

3 服务质量优化效果预测分析

在服务质量评价的基础上，使用机器学习的方法对4种公交方式进行乘客满意度发展预测，并对主要优化指标进行敏感性分析，可以检验指标优化对整体服务质量的提升效果。为避免预测过程破坏特征变量间的潜在影响关系，本文从回归预测角度入手，通过对比多方法的预测准确率，选取最优方法进行服务质量优化预测。

3.1 不同方法预测效果对比

为实现公交服务质量的精准预测，将2015—2018年的4 种公交方式问卷调查数据作为数据集进行机器学习，选取深度学习方法中预测效果较好的长、短时记忆神经网络(Long Short-term Memory,LSTM)、多层感知器(Multi Layer Perceptron,MLP)，与支持向量机(Support Vector Machine, SVM)分别基于Matlab平台建立回归预测模型。

经过多次学习训练，确定了各模型最优结构及参数：LSTM 神经网络中隐含层单元为100 时模型趋向稳定，激活函数设为ReLU 时模型梯度阈值为1，防止了梯度爆炸；MLP 模型激活函数为ReLU时，隐含层单元数为80，模型效果较好；SVM 选用RBF核函数，对应惩罚因子C值为4.8，核函数映射半径γ为1.6，模型精度最高，预测结果相对较准确。采用交叉验证(Cross Validation,CV)对各模型的机器学习效率进行检验，如图5所示。

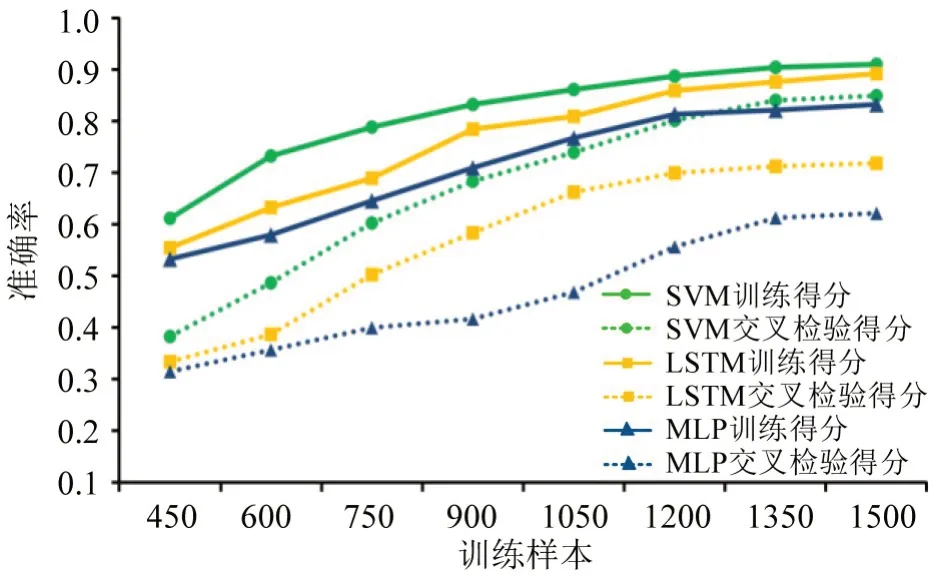
图5 各模型学习效率检验Fig.5 Effectiveness test of each model learning

在模型学习效率检验中，同一模型的训练得分(Training Score)与交叉检验得分(Cross-validation Score)曲线越接近表示模型拟合程度越好，预测精度越高。图5显示：SVM 回归预测模型的训练得分、交叉检验得分均高于LSTM 与MLP 模型，样本数为450～600时模型训练效果提升较明显，准确率由0.611 提升至0.732，交叉检验得分始终平稳增长，总体拟合效果最佳；LSTM 神经网络预测的拟合效果优于MLP 模型，但测试集的交叉验证得分与训练集得分差距较大，精度较低；MLP模型验证得分最高为0.621，远低于其他模型，不适合进行预测分析。在此基础上，选取平方相关系数R2、平均平方误差(Mean Squared Error,MSE)对各模型进行多尺度检验，即

式中：为第i个预测值；为第i个均值；yi为第i个真实值；RM为模型的MSE值。R2越接近于1表示模型拟合程度越好；与之相反，MSE值越低表示模型预测越精准。针对4 种公交方式的LSTM、MLP、SVM 回归预测模型分别进行检验，结果如表6所示。

由表6可知，LSTM、MLP、SVM 对于各公交方式服务质量预测的R2均大于0.7，较传统的SVM模型表现出了良好的拟合效果，R2均大于0.8，且MSE相对较低，更适宜于回归预测。LSTM与MLP具有独特的神经网络结构，学习速度较快，但较多的特征变量为神经网络的学习带来了难度，SVM则通过核函数将特征变量投射至高维空间，由少数支持向量决定变量特征，从本质上避免了特征维数带来的准确度影响，且在预测过程中能避免破环TAN贝叶斯网络推理得出的影响因素间潜在关系，因此，本文选择SVM建立服务质量回归预测模型。

表6 不同模型的训练拟合效果评价Table 6 Evaluation of training fitting effect of different models

3.2 SVM回归预测

SVM 回归主要通过使用核函数的非线性变换，将输入的空间投射至高维特征向量空间，再寻求一个高维空间中的超平面，令样本至超平面的距离达到最小，使回归结果最优[10-11]。本文以乘客总体满意度作为SVM 预测目标变量，其他指标作为输入变量，给定样本集S={(xi,y)|i=1,2,…,n} ，构造回归函数公式为

式中：y为目标变量，即乘客满意度；n为样本总数；xi为第i个输入变量；X为输入变量组成的矩阵；wi为第i个输入指标的参数；WT为各参数组成的参数向量转置矩阵；b为常数。

对回归函数进行Lagrange 优化，非线性超平面为

式中：w为各指标参数wi组成的向量，超平面中增加了松弛变量ξi与惩罚因子C，C可调整模型误差，也决定了样本离群点对预测的影响。本文选取处理非线性问题效果较好的径向基核函数K(x,xi)将优化后的对偶问题式转换至高维空间，求解得出回归函数，即

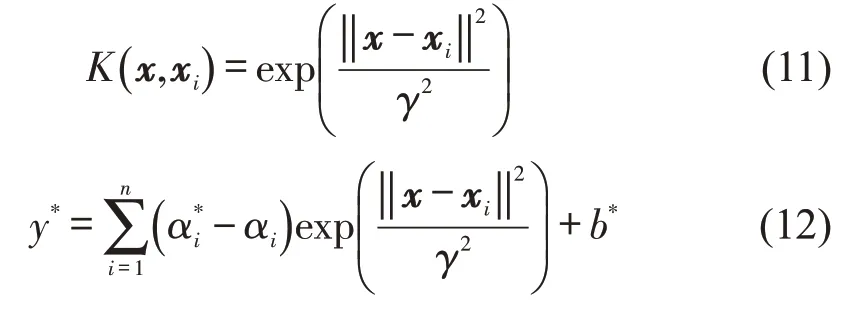
式中：γ为核函数的映射半径；y*为目标变量的预测值；αi与α*i均为Lagrange因子，与它们对应的样本为支持向量；b*为常数。在实现式(11)和式(12)时，采用文献[12]中的交叉验证(Cross Validation,CV)法寻求模型最优参数C与γ。在得出最优参数后对C、γ取对数，使模型交叉验证(CV)中的MSE 值达到最低，保证测试集总体预测准确率最优，分别对4种公交方式的服务质量优化进行预测效果检验，结果如表7所示。

表7 预测检验结果Table 7 Results of prediction test

参数优化后的各模式公交预测误差较小，除了检验模型参数，本文还将各公交方式以年为时间单位，分别对总体乘客满意度进行预测并与实际值对比，组1 为2015年目标变量预测值与2016年实际值之差，组2 和组3 以此类推。根据预测值与实际值的对比结果，可知各公交方式预测结果与真实值的相对误差均低于10%，预测精准度较高，证明了SVM 具有泛化能力强和准确率高的特点，运算中选取径向基核函数有助于处理具有离散特征的问卷数据，可基于预测对各主要优化指标进行敏感性分析。

3.3 预测结果分析

总结各公交方式乘客满意度的预测结果，并与2018年的实际值对比。结果显示：市区线路预测值为0.822，比2018年实际值0.808下降了0.016；郊区线路预测值为0.802，较实际值0.766 下降了0.036；快速公交预测值0.886 与实际值0.875 相比提升了0.011；定制公交预测值0.847 相较于实际值0.8156增长了0.031。

根据预测满意度的变化情况可按照郊区线路、市区线路、快速公交、定制公交的顺序依次提升服务质量。在SVM 回归预测的基础上，采用OAT(One-At-a-Time)方法对IPA分析得出的各公交方式服务质量主要因素进行敏感性分析，OAT方法是通过控制变量输入值的变化，探究输入变量对预测变量影响的敏感程度，结果如图6所示。

图6 敏感性分析结果Fig.6 Results of sensitivity analysis

敏感性分析中的正、负影响为指标优化减少的负影响百分比，对该公交方式总体满意度的正向影响程度。市区线路的候车时间（A3）与车厢拥挤状况（E10）的服务水平优化对总体影响程度最大，A3负影响每减少17.8%使整体满意度提升39%；E10每减少28.6%的负影响可使满意度总体提升36.4%；B1、B2、C2和E6的优化可以有效提升满意度，但效果均低于20%，对整体的影响能力较有限，因此，候车时间与车厢拥挤状况为市区线路应主要优化的服务质量影响因素。

由图6可知，郊区线路主要优化指标为乘车时长（A1）、候车时间（A3）和车厢拥挤状况(E10)，满意度提升空间分别为34.9%、32.2%和29.4%；定制公交主要优化指标为乘车时长（A1）和车厢拥挤状况（E10），改变较少的负影响能得到总体满意度较大的提升；快速公交敏感性分析显示车速稳定程度（B1）与车厢拥挤状况（E10）对整体影响较大，但服务水平优化过程对E10的投入需求要大于B1，由此可知，敏感性分析结果可为优化资源投入比重提供参考。

在此基础上，结合各公交方式实际交通状况与各影响因素间的潜在影响关系(图3)，依次提出服务质量优化措施：

(1)协调4 种公交方式在通勤高峰期的发车数量、时间间隔，根据各方式公交需求量更改发车频次，扩大城郊公交线路覆盖率，并建立基于移动端的公交综合信息平台，提供车辆实时位置及车内人数信息。

(2)对市区、郊区的公交线路及站点按照乘车需求进行重新调整，根据居民出行特点修改首末班时间及发车频率，并在原有投币箱和IC 卡机基础上开拓基于不同平台的电子支付渠道，支持预先网络购票乘车，缩短乘客上下车时间以优化候车时间及乘车总时长。

(3)增加公交线路改造、技术升级和人员培训等方面的投资，针对郊区线路、快速公交和定制公交的驾驶人员定期进行行车安全培训，建立公众参与的评价考核机制。

(4)完善快速公交站点内的慢行设施设置，加快站内客流的集散速度，并在冬季及时更换车辆雪地胎、控制整体车速的平稳，避免出现危险驾驶。

(5)针对部分定制公交线路，缩短客流量较大的站点位置与其他公交方式站点的接驳距离，并调整部分冷僻站点及相应线路的设置，提升换乘便利性，且发挥定制公交对城市骨架交通网络辅助、补充的作用。

4 结论

本文以TAN 贝叶斯网络与SVM 为基础，以多方法组合的形式，从评价及预测角度探究了乘客视角中多模式公交服务质量的差异性，研究结果表明：

(1)各模式公交服务质量存在显著差异，同一指标的影响能力、优化效果在不同公交类型中也具有差异性；指标间潜在的影响关系与公交自身基础设施、服务水平密切相关；所有公交方式的便利性指标间均有较强关联，不同维度指标也存在相互作用的非逻辑性关系。

(2)在乘客视角中，各维度均存在影响出行体验的因素，其中，车厢拥挤问题长期存在于各模式公交的服务中，市区线路的指标优化效应最佳，正效应为36.4%，应率先对其进行优化；在行车安全方面，快速公交乘客对车速稳定因素较为敏感，优化后可提升42.7%的乘客满意度。

(3)便利性是乘客选择公交出行的重点考虑因素，除快速公交外，其余公交方式均存在便利性问题，郊区线路与市区线路、定制公交分别存在乘客候车时间及乘车时长的问题，且指标优化正效应均大于30%，因此，协调不同公交方式的发车计划有助于提升整体的乘客满意度。

(4)通过多方法对比及实例分析，验证了多方法组合模型的有效性，模型检验结果显示：TAN 贝叶斯网络的分类准确率均大于80%；相对传统的SVM 回归预测模型预测误差均低于10%，拟合效果优于MLP 与LSTM 神经网络，预测准确率高；表明多方法组合的分析模式结合了各方法的优势，适用于多类型公交服务质量的评价及优化检验。