一种保障高空作业平台稳定性的重心分配方法

邓 彧，陆进添，谢仁军

（三一帕尔菲格特种车辆装备有限公司，江苏 南通 226000）

剪叉式高空作业平台在前进或后退的过程中，若遇到坑洼地面，则会有发生倾翻的危险。因此，为保证其安全性和稳定性，则需要研究整机的重心分布范围，以确保整车能够满足在前进和后退时陷入坑洞均能保持稳定，不发生倾翻。

1 坑洞稳定性分析

剪叉式高空作业平台陷入坑洞的过程如图1所示，载荷按最危险情况放置，即将额定人员质量与额定延伸平台工具质量载荷均集中放置于可延升的平台的最前端，基本平台额定工具质量载荷集中放置在基本平台最前端，转向轮与机身方向平行并以最大允许速度v前行，直至车轮陷入坑洞，支撑从车轮支撑变为坑洞防护板支撑。此时如图2 所示，若忽略因状态的改变而引起的结构变形，则车身整体绕后轮中心A转动的角度

图1 陷入坑洞的过程

图2 陷入坑洞瞬间整车的倾斜角度

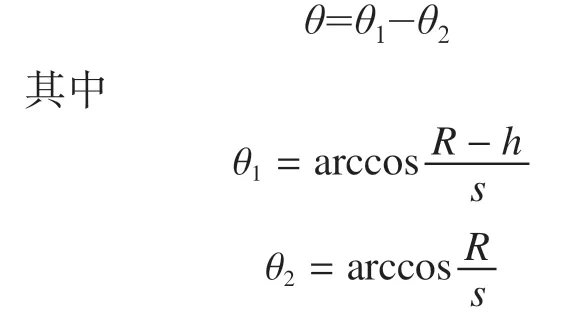
R为车轮半径，h为坑洞防护板的离地高度，s为车轮中心到防护板支撑点的距离。

剪叉式高空作业平台陷入坑洞后会经历图1 所示的①和②两个过程，此后，剪叉式高空作业平台若不倾翻，则会绕着坑洞的防护板支撑点B晃动，并在阻尼力作用下将机械能完全消耗后静止。

图3 前进和后退工况

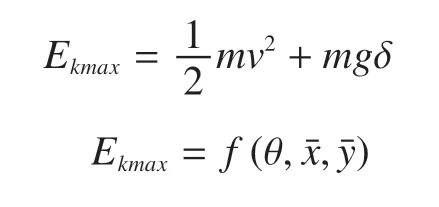
此后整车又绕支撑点B晃动，当重心能够越过倾翻线时发生倾翻，若需要保障整车的安全性，则不应越过倾翻线，即需要保证：所获得的最大动能小于使重心越过倾翻线所需要的势能。

设Δ 为重心上升的高度，如图4 所示，ε为重心到倾翻线的水平距离

图4 重心升高示意图

由图1 可知ε是转过角度θ和重心的坐标为函数，从而Δ 也是转过角度θ和重心的坐标为函数。若使整车越过倾翻线，则需要增加的势能为

若需保障整车的安全性，则有

2 重心分配方法

对于整车在行驶过程中陷入坑洞的分析，因重心距离车头和车尾存在较大差异，因此需要考虑前进和后退两种情况，并按照最危险的载荷工况进行分析，因此，平台载荷的作用位置不同，重心会随工况而发生变化，而对于同一辆车无论前进还是后退，其底盘、叉架和外平台是不变的，因此可将整车分为两部分质量来研究，即不变部分和变化部分。

如图3 所示，设前进过程不变部分、变化部分的质量分别为m1、m2，重心坐标分别为（x1，y1）、（x2，y2），则后退过程重新建立坐标系，在x′oy坐标系中不变部分、变化部分的质量分别为m1、m2，重心坐标分别为（x′1，y1）、（x′2，y2），由于整车长度L确定，不变部分重心不变，则有

设稳定临界点时整体重心到运动方向最前端的水平距离为x0，则前进或后退时为保持稳定，需要重心到运动方向最前端的水平距离大于x0

即水平重心范围

横坐标应满足

可得临界距离

再将临界水平重心距离带入公式（1），可得临界竖直重心y0，而转动的角度θ则由坑洞的保护板的位置和尺寸确定。

为保证前进和后退时陷入坑洞的稳定性，整体的重心应满足

又由于m1、m2、x2、y2是由设计目标所确定的确定值，所以可确定可变部分在任意可行位置时不变部分的重心分布范围为

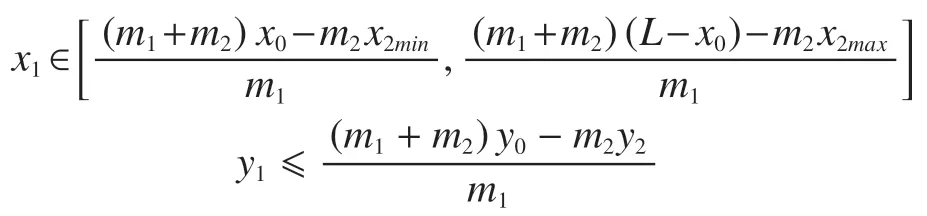
配重部分和结构件部分共同构成质量不变部分，而质量不变部分在图3 坐标系中的重心范围可由上式确定。

由此，在上式所确定范围的基础上对质量不变部分进行质心计算可得对应配重放置位置。设配重质量和结构件质量分别为m3、m4，配重及结构件重心坐标分别为（x3，y3）、（x4，y4），于是

其中，m3+m4=m1，（x4，y4）为已知的结构件的设计重心，可得配重在图3 坐标系下的横纵坐标值分别为

由此，可用确定配重的方式来平衡整机维持稳定时所需满足的重心关系。

3 结论

本文以动能与势能相互转化的原理为基础，进行了剪叉式高空作业平台维持稳定的重心分配的分析与计算，得到了作业车整机不变部分的重心分布范围，进而确定配重的放置位置，以满足剪叉式高空作业平台在前进和后退过程中的安全性和稳定性，能够在总体设计阶段就确定出大总成的重心位置，从而提高设计效率，避免返工。