基于Copula函数的珠江三角洲上游来水丰枯遭遇分析
张赵毅,何艳虎,2*,林柱良,陈晓宏
(1.广东工业大学环境生态工程研究院,广东 广州 510006;2.广东省流域水环境治理与水生态修复重点实验室,广东 广州 510006;3.中山大学软件工程学院,广东 珠海 519082;4.中山大学水资源与环境研究中心,广东 广州 510275)
河流径流量的丰枯变化对水资源的配置与管理有着重要的影响[1]。一方面,受自然地理特性和人类活动等影响,流域内径流的丰枯变化存在着客观的差异性和不确定性;另一方面,由于全球气候变化影响的深入,极端气象事件发生的强度和频率增加,降水量空间异质性增强,从而使得流域径流量的时空分布发生变化[2],径流丰枯遭遇特性复杂多变。因此,研究流域径流丰枯组合遭遇对变化环境下的水资源配置与管理有着重要的理论与现实意义。
常用的河川径流丰枯组合分析方法有Moran法、EFM法、FEI法、贝叶斯网络理论方法、集对分析法、Copula函数方法等。如陈长清等[3]基于贝叶斯网络对塔里木河流域三源流和塔里木干流的年径流量等进行研究;李继清等[4]采用集对分析法和常规法对长江中上游各地区的径流进行了丰枯分类;马秀峰等[5]使用游程理论分析了丹江口水库和郑州地区的4种径流丰枯遭遇情况。不难发现,这些方法均能计算出研究区域的丰枯遭遇情况,但对于水文事件中多变量的处理能力略有不足。由于地理位置与气候条件相近,同一流域下的河流之间,其径流过程多具有一定的相依性。因此,构建多维联合分布模型使对同一流域下多条河流进行径流丰枯组合分析成为可能。
多维Copula函数作为一种多变量连接函数,相较于联合分布法、多元正态分布法、非参数方法等[6]多变量水文分析方法,其对分布特性不同的要素具有同等的适应性,打破了其他多变量分析方法的局限,已经在多维联合分布中得到了广泛应用。涂新军等[7]利用阿基米德Copula函数构建了枯水径流联合分布模型,对珠三角西水东调的西江缺水风险进行了分析;吴海鸥等[8]基于Copula函数对鄱阳湖水系径流丰枯遭遇进行了多维分析,探讨了鄱阳湖水系多维丰枯遭遇同步联合概率的变化特征;张倩等[9]使用Copula函数对郑州市南水北调工程及黄河来水进行了补偿特性计算分析,认为两水同枯的风险最大,易造成供水短缺问题;Thilakarathne等[10]利用Meta-elliptical Copula函数对湄公河下游流域进行了干旱分析,认为未来湄公河下游流域干旱事件将更加严重。
珠江三角洲城市群是粤港澳大湾区重要组成部分,水系发达、产业集聚、人口稠密,枯水期供水受上游西江、北江、东江来水变化和下游咸潮上溯影响,水资源供给安全保障面临严峻挑战。研究三江来水的丰枯遭遇组合,有利于在枯水期进行水资源分配和调度,保障三角洲城市群供水安全。因此,本文选用Copula函数对三江年、汛期及非汛期径流的二维及三维丰枯组合进行计算分析,研究三江的径流丰枯同步性及枯水期可能的丰枯组合,并求出对应丰枯条件下的各月径流量,以期为珠三角城市群水资源配置提供科学依据。
1 方法与数据
1.1 研究区概况与基础数据
珠江三角洲(下称珠三角)位于广东省中南部,是由复杂河网形成的冲击平原,区域内包括广州、深圳、珠海、佛山、江门、肇庆、东莞、惠州、中山9个城市,总面积达5.5万km2,是中国经济和社会开放度最高、活跃度最强的地区之一,在国家发展战略中具有重要地位[11]。珠三角地区的主要水系为西江、北江、东江和珠三角诸河水系(图1),珠江流域面积达45万km2,西江、北江、东江为珠江的三大支流[12],珠江三角洲位于三江的河流下游。珠江三角洲水资源丰富,其总量达3 402亿m3[13],其中来自西江、北江、东江的过境水量达2 941亿m3。
研究分别选取马口、石角、博罗水文站作为西江、北江和东江的控制站。马口站集水面积为353 120 km2,地处西、北江三角洲的顶端,是西江进入珠三角的首个控制站;石角站集水面积为38 363 km2,占北江流域总面积的82.1%,是北江中下游总控制站[14];博罗站集水面积为25 325 km2,占东江流域总面积的71.7%[15],是东江下游控制水文站。所选用水文站点均具有代表性。
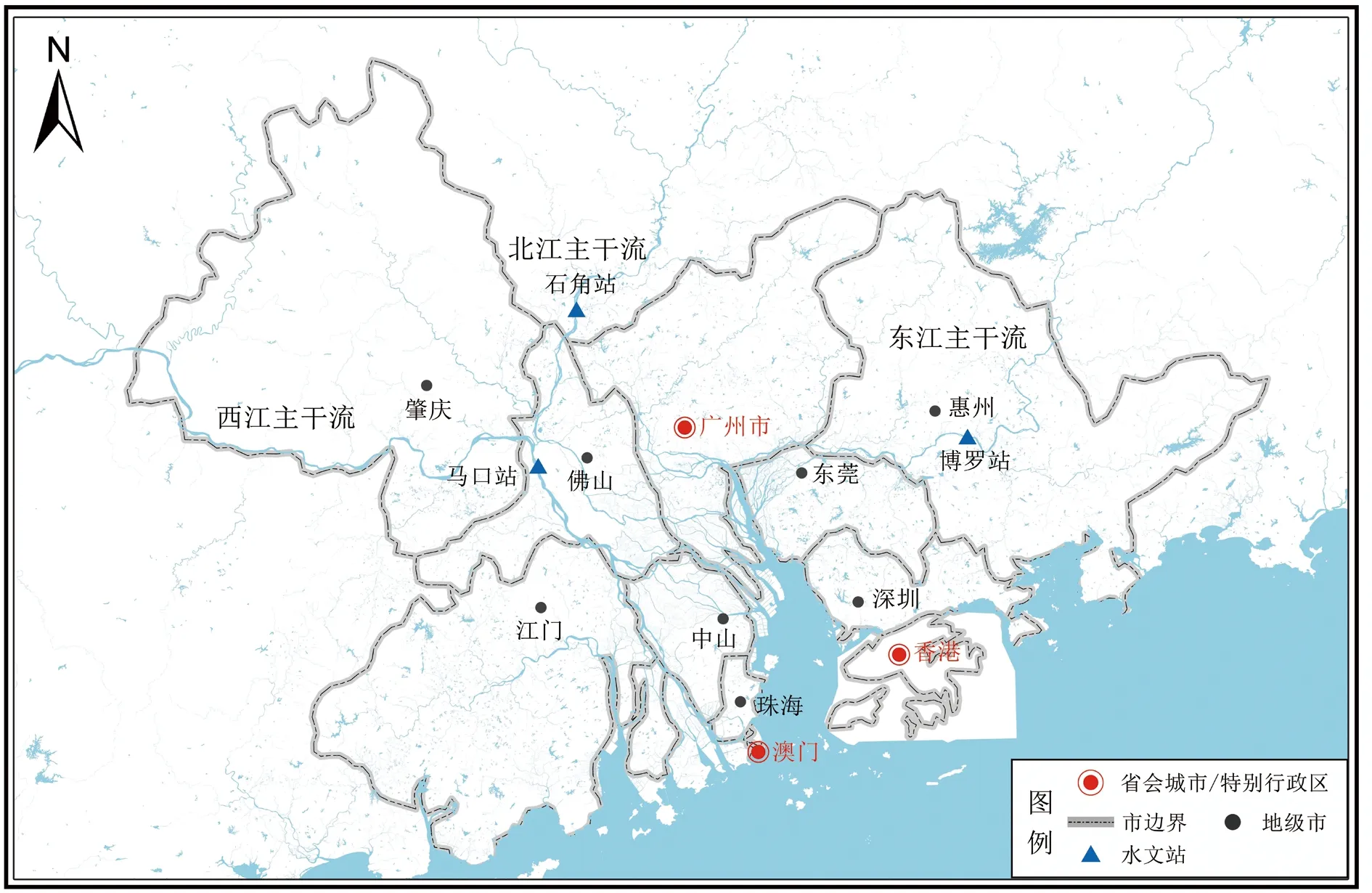
图1 研究区域与水系
根据实际情况,以4—9月为西江、北江和东江的汛期,以10月至次年3月为非汛期。以1959—2008年的月平均流量作为基础数据,并在此基础上计算出三江河流的年、汛期和非汛期径流的径流模数、径流模比系数参数值。径流模数常用于对不同流域的径流进行比较,经计算得出,西江、北江和东江的多年平均径流模数分别为0.020 4、0.025 5和0.021 4 m3/(s·km2),且三江汛期径流模数均约为非汛期径流模数的3倍,因此三江的丰枯特征具有一定的关联性。
1.2 方法原理
1.2.1Copula函数
Copula函数基于Sklar[16]定理,可看作边缘分布在[0,1]上均匀分布的随机向量的联合分布函数。常用的多元Copula函数有多元正态(Gassian Copula)函数[17]、多元t-Copula函数[18]和阿基米德Copula函数3类,其中阿基米德Copula函数又包括Clayton Copula[19]、Frank Copula[20]和Gumbel Copula[21]3种主要函数。5种Copula函数公式如下。
Gassian Copula函数的公式为:
C(u1,u2,…,un;R)=ΦR(Φ-1(u1),Φ-1(u2),…,Φ-1(un))
(1)
式中R——相关系数矩阵;ΦR——n元标准正态分布的分布函数;Φ-1——标准正态分布函数的逆函数。
多元t-Copula函数的公式为:
(2)
式中R——相关系数矩阵;tR,k——n元t分布的分布函数;k——自由度。
Clayton Copula函数的公式为:
C(u1,u2,…,un;θ)=(u1-θ+u2-θ+…+
un-θ-1)-1/θ
(3)
式中θ——函数拟合参数,θ∈[0,+∞)。
Frank Copula函数的公式为:
C(u1,u2,…,un;θ)=
(4)
式中θ——函数拟合参数,θ∈R。
Gumbel Copula函数的公式为:
C(u1,u2,…,un;θ)=exp{-[(-lnu1)θ+
(-lnu2)θ+…+(-lnun)θ]1/θ}
(5)
式中θ——函数拟合参数,θ∈[1,+∞)。
采用均方根误差RMSE、赤池信息量准则(Akaike Information Criterion,AIC)进行Copula函数优度检验,以确定最优的Copula函数。检验方式的函数公式为:
(6)
AIC=nln(MSE)+2l
(7)
(8)
式中Pei——经验频率;Pi——理论频率;n——径流序列的样品大小;l——边缘分布函数参数个数。
RMSE与AIC的数值越小,说明Copula函数计算的联合分布概率值越靠近经验概率值,拟合效果越好。
1.2.2边缘分布
为应用Copula函数,首先用适宜的边缘分布描述各单个变量。常用的边缘分布函数及分布拟合曲线有正态分布 (NORM)、泊松分布(POISS)、极值分布(EV)、广义极值分布(GEV)、伽马分布(GAMMA)、韦布尔分布(WBL)、广义帕累托分布(GP)等函数。采用极大似然公式进行三江径流分布函数的参数估计,公式为:
(9)
(10)
(11)
式中L(θ)——似然函数;F(xi;θ)——边缘分布密度函数,θ为待估算参数。
应用Kolmogorov-Smirnov(K-S)作各边缘分布拟合优度检验,确定边缘分布函数。根据显著性检验原则,取0.05显著性水平,P值大于0.05,则肯定原假设,认为径流分布与选定拟合的分布函数相同,选定分布函数可用作径流分布拟合。
1.2.3丰枯遭遇分析
常用的丰枯划分方法一般基于距平百分率划分枯、平、丰来水,或者基于径流累积频率(P),如以频率37.5%、62.5%或频率25%、75% 作为分界线划分枯、平、丰3种水平年。为了细分丰枯来水,本研究采用水利部颁布的《地表水资源调查和统计分析细则》中的相关规定,以径流累积频率(P)12.5%、37.5%、62.5%、87.5%为分界线将径流划分为特枯来水(0% 在构建的Copula函数为二维结构时,设径流量为X,P频率对应的水量为Xp,Pk对应丰枯分级的数值偏小端,Pf对应丰枯分级的数值偏大端,当二维结构下两河流流量分别是X和Y,边缘分布分别是u和v。可以推导出二维联合分布概率的公式为: P(Xpk (12) 同上,在三维Copula结构下,3条河流流量分别为X、Y、Z,边缘分布分别为u、v、w,可以推导出三维结构下的联合概率公式为: P(Xpk (13) 2.1.1年、汛期和非汛期径流量边缘分布的确定 运用式(9)—(11)对三江的年、汛期和非汛期径流的7种边缘分布函数进行拟合,并利用K-S方法进行显著性检验,得到的P值见表1,P值越大,显著性越高,拟合效果越好。 表1 边缘分布函数拟合显著性 由表1可知,泊松分布和广义帕累托分布均没有通过显著性检验,其他分布函数对变量要素分别有不同的拟合效果。对西江年径流拟合较好的有正态分布、广义极值分布和韦布尔分布;对西江汛期径流拟合效果较好的有正态分布、广义极值分布和伽马分布;对西江非汛期径流拟合效果较好的只有广义极值分布。对北江年、汛期和非汛期径流拟合效果较好的有广义极值和伽马分布函数。对于东江年径流和汛期径流拟合较好的有正态分布和广义极值分布函数;而东江非汛期径流拟合效果较好的有广义极值分布和伽马分布。分布函数拟合见图2,根据拟合情况与P值大小选取每个径流要素的最佳边缘分布函数,并对最终选用的函数作密度概率函数图(图3)。 a)年径流 d)年径流 g)年径流 a)年径流 径流边缘分布函数的选用及参数见表2。表2中分别代表三江径流年、汛期和非汛期径流的模比系数值。 表2 西江(F1)、北江(F2)、东江(F3)径流边缘分布函数及参数 2.1.2月径流量边缘分布的确定 对三江月径流进行边缘分布函数拟合,用于确定不同丰枯组合下的西江、北江和东江月径流量。根据边缘分布函数的显著性检验结果(表1和图2),广义极值分布对三江径流要素都具有较好的拟合度,因此使用广义极值分布对三江月径流进行拟合,月径流边缘函数拟合曲线见图4。图中蓝色曲线为月平均模比系数的经验累积概率曲线,红色曲线则是对应的边缘函数拟合曲线。 图4 西江(F1)、北江(F2)和东江(F3)月径流分布函数拟合 2.2.1二维Copula径流联合分布 将西江、北江和东江的年、汛期和非汛期径流分别两两组合,依次采用五种Copula函数对联合分布函数进行参数估计和拟合检验(表3)。在二维Copula拟合中,Frank Copula函数的检验值比其他Copula函数都小,且对所有的径流要素都呈现较好的拟合度。因此选用Frank Copula函数作为二维径流丰枯拟合函数。通过图5可知,三江年径流丰枯具有较高的同步性,当一条河流出现特枯(或特丰)时,其他河流出现特丰(或特枯)的概率几乎为零。 依据式(12)计算出二维来水丰枯组合的概率值(图6)。可以发现,同丰枯组合1、7、13、19、25的联合概率较其他组合大,说明当一条河流出现某一种丰枯类型,另一条河流出现相同的丰枯类型的概率总是最大的。 西江和北江、西江和东江、北江和东江的年径流同步概率分别为0.448 2、0.340 4、0.350 5;汛期径流同步概率分别为0.475 0、0.369 9、0.246 7;非汛期径流同步概率分别为0.264 4、0.423 6、0.273 9。说明西江和北江年径流及汛期径流同步性比西江和东江、北江和东江大。而在非汛期,西江和东江、北江和东江的丰枯同步性更加强烈。二维丰枯同步的5种组合概率和都接近或者超过0.3,相比二维丰枯异步其他组合的概率,呈现了较强的丰枯同步性,证明了西江、北江和东江之间较强的丰枯同步关系。 表3 西江(F1)、北江(F2)和东江(F3)Copula函数二维联合分布参数估计及拟合检验结果 a)F1-F2 a)年径流 d)年径流 g)年径流 2.2.2三维Copula径流联合分布 选取了3种阿基米德Copula函数进行三维来水丰枯联合分布参数估计及拟合检验(表4)。 由表4可知,Frank Copula函数的RMSE和AIC最低,因此选用Frank Copula函数作为三维Copula函数进行来水丰枯组合分析。采用式(13)计算125种三维来水丰枯组合的概率值,结果见图7。在年、汛期和非汛期径流尺度上,三江径流同丰枯的概率分别为0.085 7、0.086 0、0.068 5,比二维组合下的同丰枯概率值小,说明三江来水同丰枯的概率较二江来水同丰枯概率降低。三维组合中,1(同特枯)、32(同偏枯)、63(同平水)、94(同偏丰)、125(同特丰)是同丰枯组合,年径流的概率值分别为0.006 5、0.024 7、0.018 1、0.027 3、0.009 2,并且从图7可知,同偏枯、同平水和同偏丰的组合概率较其他组合概率都偏大,但由于丰枯异步组合数量多,因此同丰枯组合总体概率较低,即三江径流同步丰枯相对而言属于小概率事件。且较高概率的丰枯组合大部分集中于32—94的组合区间,说明任意组合中,有2条河流出现偏枯或平水或偏丰是较大概率事件。在年、汛期和非汛期径流尺度上,同特枯和同特丰都是概率值极小的组合,相对而言,出现“特枯-特枯-偏枯”和“特枯-偏枯-偏枯”的概率值更大,是枯水年更有可能的丰枯组合。 表4 西江(F1)、北江(F2)、东江(F3)Copula函数三维联合分布参数估计及拟合检验结果 根据边缘分布函数和三维丰枯联合概率计算结果,得到三江同步丰枯组合下的联合概率、年平均流量(表5)和月平均流量(图8)。 a)F1 b)F2 c)F3 表5 西江、北江和东江年径流同步丰枯组合 b)F2 c)F3 由表5与图8可知,在同特枯或同偏枯来水条件下,三江年平均流量能达到同平水来水条件下的55%或77%,但三江非汛期(1—3月、10—12月)流量处于较低水平,说明三江在汛期仍能提供较为充足的来水,但在非汛期三江同枯遭遇,上游来水减少,珠三角城市群面临水资源短缺风险。考虑到三江具有一定的丰枯同步性,且三维丰枯组合中“特枯-特枯-偏枯”和“特枯-偏枯-偏枯”的概率值较高,因此如何在上述两种丰枯组合下的非汛期,满足珠三角城市群的用水需求,将是一个值得注意的研究方向。 本文利用Copula函数构建了珠江流域三大支流西江、北江、东江的二维与三维联合分布模型,分析了三江年、汛期和非汛期径流的丰枯遭遇,计算了同丰枯组合下的三江年和月径流量。主要结论如下。 a)在二维与三维Copula函数联合分布拟合中,Frank Copula函数的RMSE和AIC检验值最小,且对三江所有径流要素都呈现较好的拟合度。 b)三江两两间径流丰枯同步的概率大于丰枯异步的概率。其中在全年和汛期,西江和北江的径流丰枯同步性较好;而在非汛期,西江和北江、北江和东江之间的径流丰枯同步性更加强烈。 c)三江三维Copula函数联合分布结果表明,随着维数的增加,三江来水同丰枯组合(同特枯、同偏枯、同平水、同偏丰、同特丰)的概率降低,丰枯异步的概率升高。同时,在年、汛期和非汛期径流角度,同特枯和同特丰都是概率值极小的组合,“特枯-特枯-偏枯”和“特枯-偏枯-偏枯”的概率值更大。 d)在“特枯-特枯-偏枯”和“特枯-偏枯-偏枯”来水条件下,三江在非汛期来水量较少,因此在非汛期,珠三角城市群将面临着严峻的供水安全问题。2 结果与分析
2.1 径流量边缘分布的确定
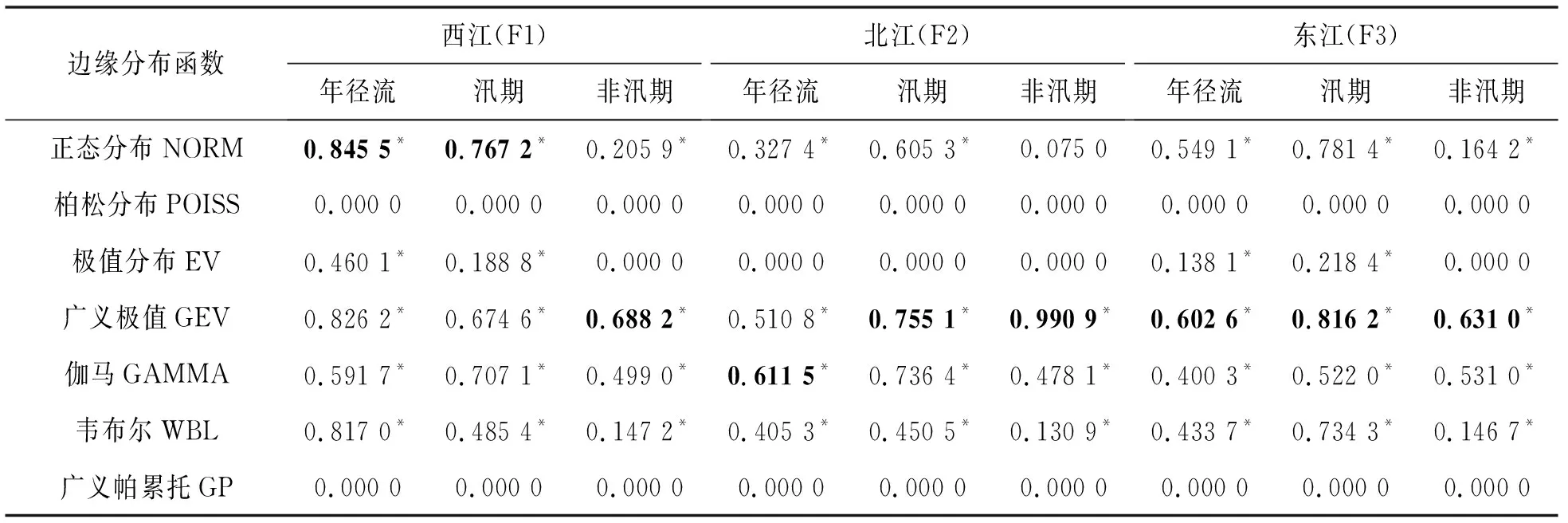
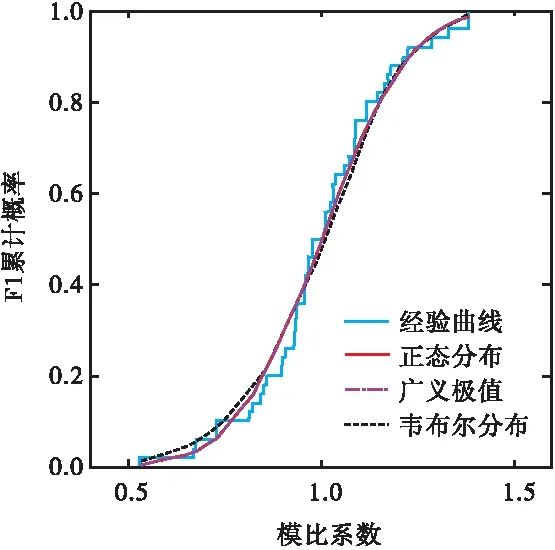

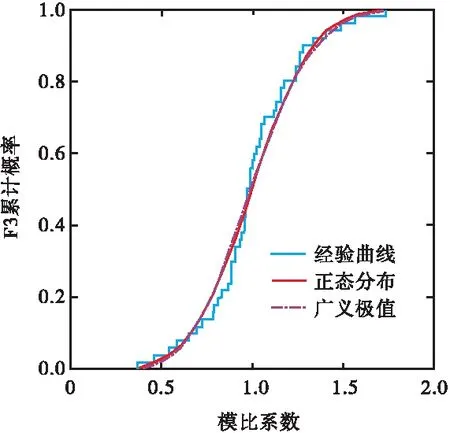
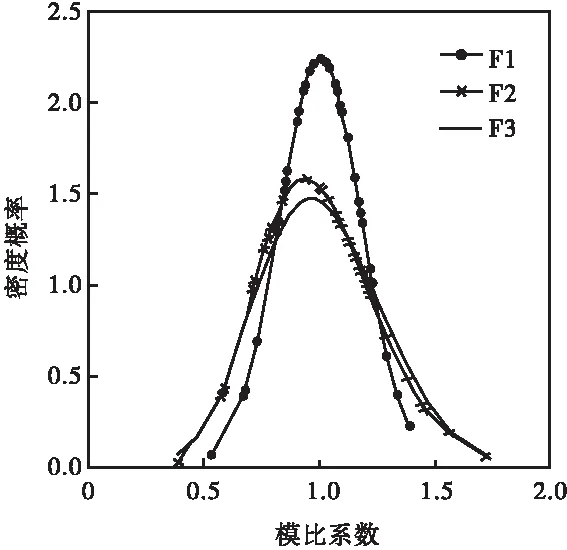

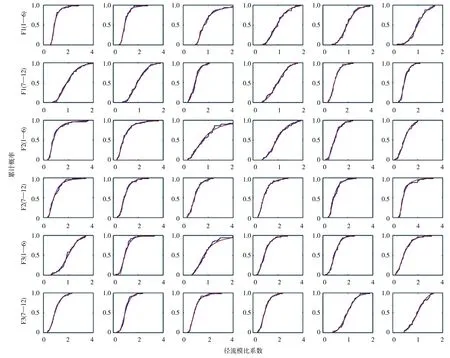
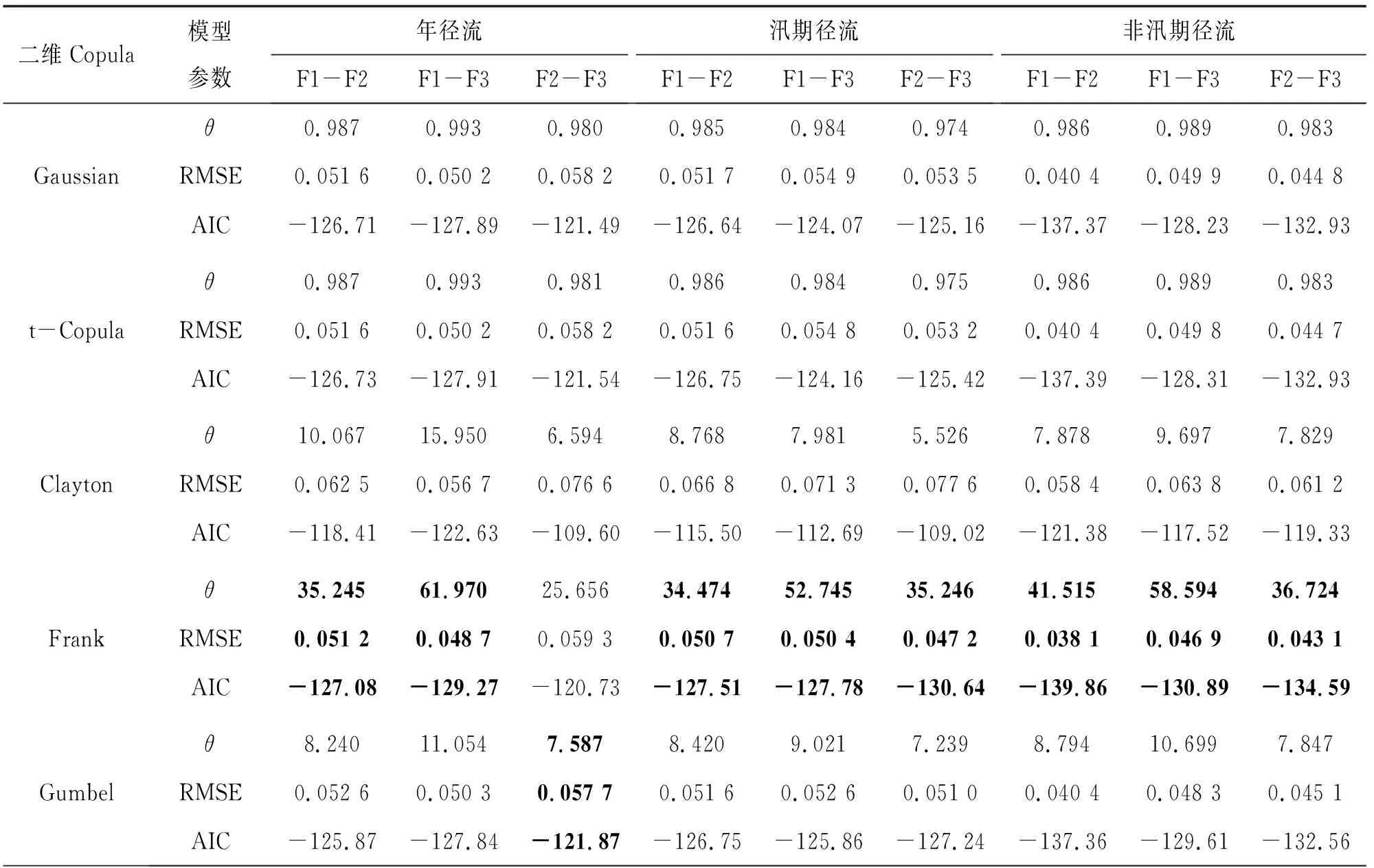
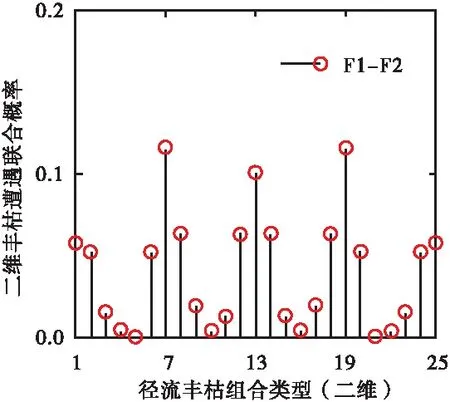
2.2 径流丰枯组合分析



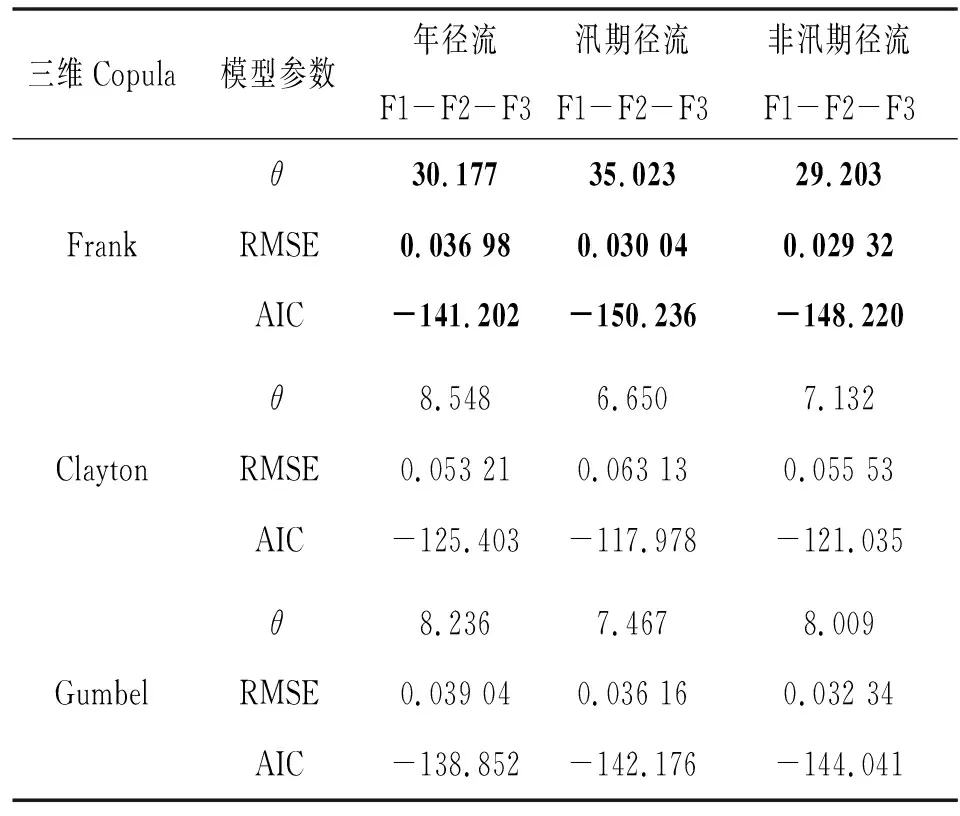

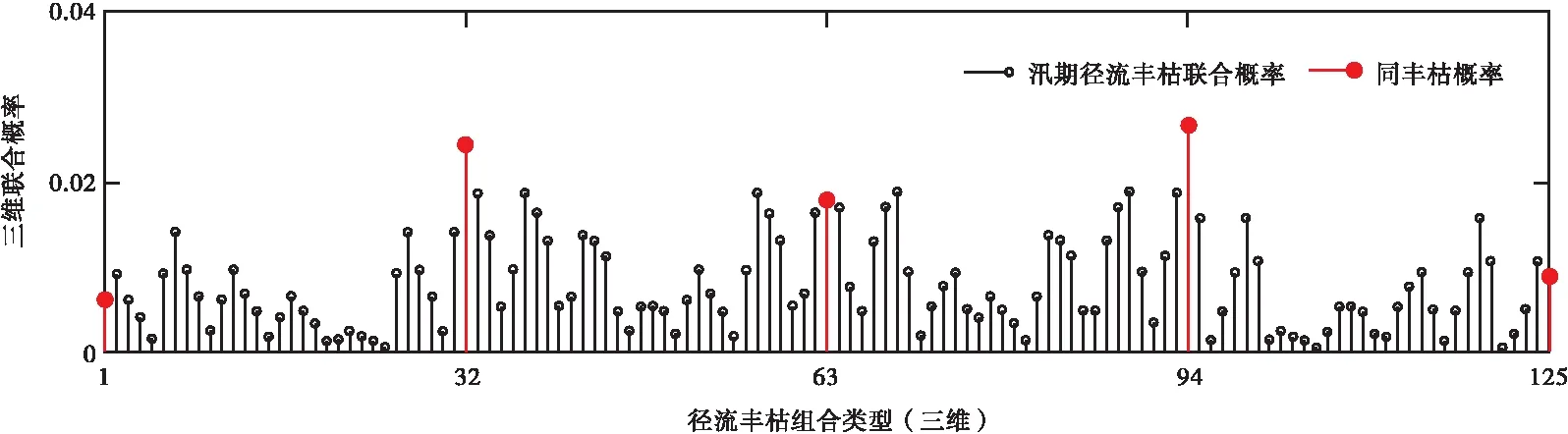

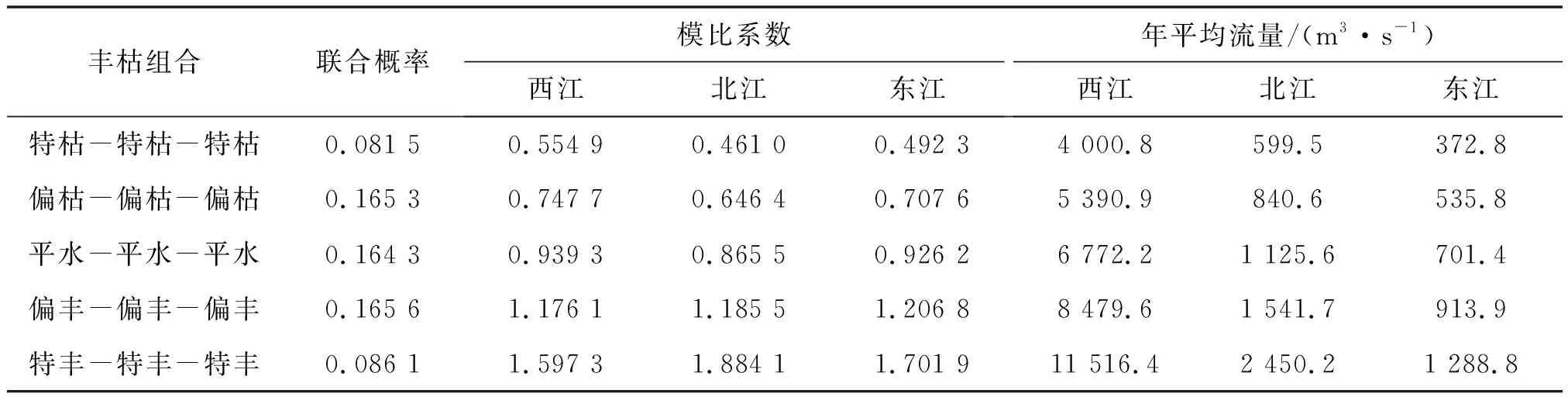
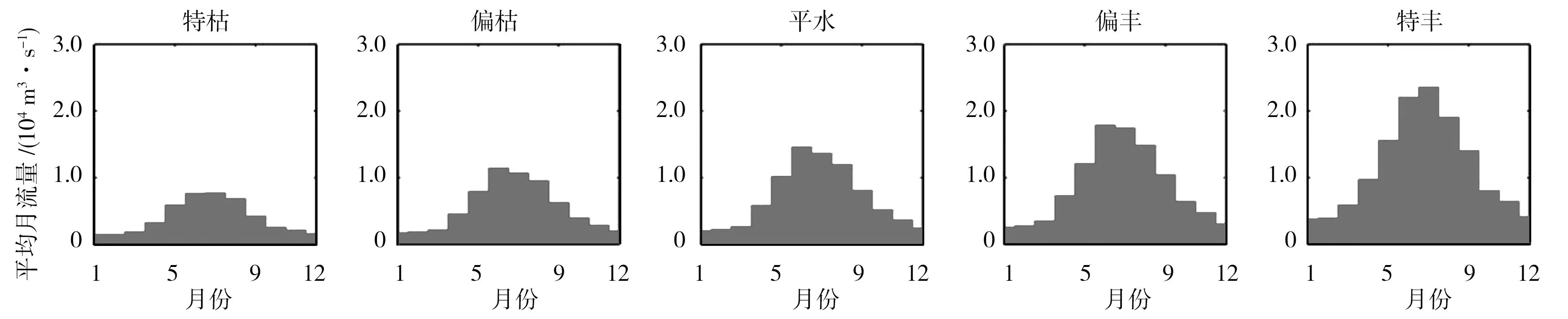
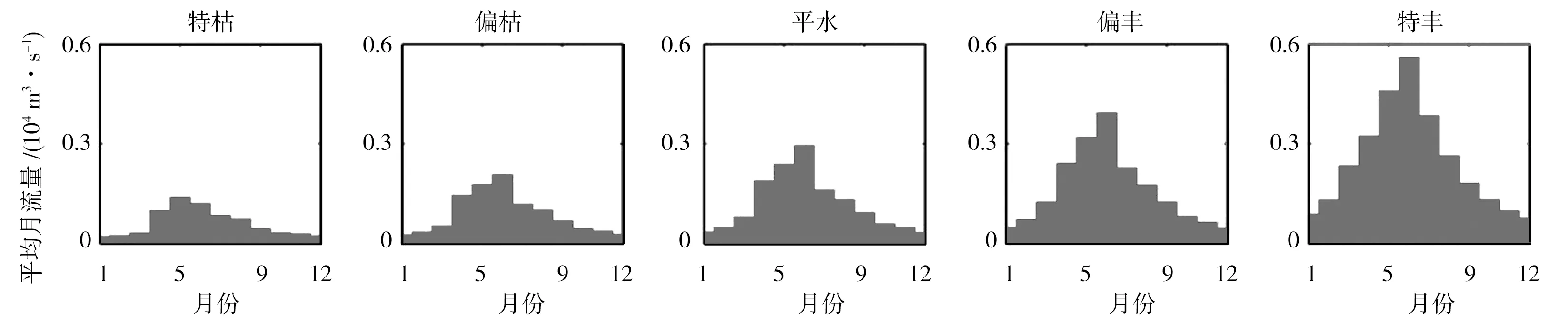
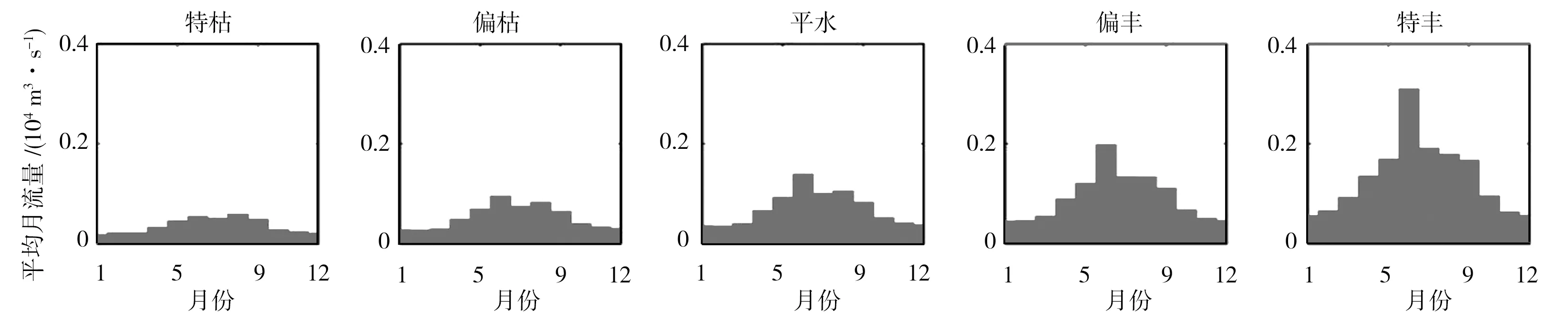
3 结论

