公路货运场站车货动态配载优化研究
张 赫,王 宇,刘 宇,邢江豪
(大连海事大学 交通运输工程学院,辽宁 大连 116026)
0 引 言
交通运输业是国民经济的主导性产业,党的十九大明确提出了建设交通强国的口号,而公路运输在各种交通运输方式中占据着重要地位,2018年公路货物运输量为395.9 亿吨,同比增长7.4 %,占货物运输总量的76.9 %。近年来,随着我国经济的不断发展,大城市外来人口的不断涌入,导致了交通不畅和拥堵,加大了城市公路物流业的负担。货车常常因为道路堵塞而延误到达货运场站取货的时间,同时由于运输企业对于车辆配货的调度安排经常是根据自身经验,缺乏合理的方法,导致车辆与货物之间无法有效配载,车辆空驶率高。因此,如何有效预测货车的周转行程时间,使得货运场站能够提前掌握返回车辆的信息,根据车辆和货物的动态信息制定配载方案,最大程度的利用货车资源,减少人力物力的浪费,提高货运场站的经济效益是目前亟待解决的问题。
在车辆行程时间预测方面,H.M.MOONAM等[1]使用K最近邻、最小二乘回归增强和卡尔曼滤波等方法从已有的数据预测未来的行程时间,并得出了卡尔曼滤波在基于道路的模型中有着更好的预测精度;R.X.ZHONG等[2]提出了一个在线行程时间预测模型,重点是捕捉异常的影响;景辉鑫等[3]针对交通流数据波动性较高和易失真的缺点,提出一种基于灰色 ELM 神经网络的短时交通流预测方法;温惠英等[4]针对行程时间波动性加入了机动车和非机动车因素,建立了阻抗函数模型;潘义勇等[5]将城市交通道路阻抗分为路段阻抗与节点阻抗两部分,分别建立模型并利用道路阻抗影响因子进行改进。
在车货配载方面,张嘉宁[6]建立了大宗商品配载问题的组合优化数学模型;L.BAJRACHARYA[7]提出了一种对分散的物流货车和货物进行最优路径分配的管理方法;李建民等[8]就车货配载问题建立了包括车辆空驶率最小、利用率最大等多目标规划模型;徐天亮等[9]建立了单车和多车配装两个数学模型并给出了算法;陈宏程[10]将车货配装和配送路径问题结合起来,设计了一种自动选择车辆类型,配载联合优化模型;侯景瑞等[11]从车主角度出发,以车主收益最高为目标函数,建立了货车配载模型,并用改进的遗传算法进行了求解;S.A.BJORGEN等[12]提出了智能货物这个新概念,以实现货源方和车源方在运输网络中的无缝互连;D.GATTUSO等[13]建立了一个随机的离散事件仿真模型来解决与车辆和货物接收相关的问题。
陆丹[14]以车辆数最小为目标,建立了静态车货配装优化模型并进行了求解;张赫等[15]建立了车辆动态配货模型并用Visual Basic软件进行了模拟。文献[14-15]都只考虑到了车辆与货物的一次配装,无法及时有效地对动态变化的车货配载问题进行求解。笔者重点在前两者的研究基础之上,结合车辆行程时间预测,并加入了对车辆维修保养因素的考虑,建立了动态车货配载模型。根据不同时间段货运场站内的货车类型和数量,对车辆和货物的配载方式进行了优化,以提高车辆利用率,优化货车资源配置,有利于货运场站做出更快、更有效的调度决策。
1 影响因素分析
1.1 货车周转行程时间
周转时间为货车从货运场站出发,到达目的地卸货和返程时间的总和。行程时间会受到各个路段交通流量、意外交通事故和天气原因等的影响,因此其为一个不确定值。通过对货车周转时间的预测,可以使货运场站实时掌握车辆动态信息,及早为预到达的车辆准备停车区以及相应工作人员和货物装卸设备,提高货运场站装卸效率,减少不必要的调度成本。因此笔者需要收集交通流量、车辆数以及行驶时间等参数。在交通流量收集方面,笔者采用人工观察法;在行程时间收集方面,采用GPS定位方法和人工记录方法相结合的办法,GPS接受信息后将数据传入计算机,从而根据行驶里程和驾驶速度计算出平均行驶时间,然后再采用人工方法用秒表记录堵车状态下的延误时间,再在表格分别记录下来,最后进行加和处理即为总的行程时间。周转时间包括3个部分:路段行驶时间用T1表示、交叉口延误时间用T2表示、目的地卸货时间用T3表示。可用公式表示为:
T=T1+T2+T3
(1)
根据定义,车辆交通占用率值等于路段上车辆的平均总长度与路段长度之比,如式(2):
(2)
该公式可转换为:
(3)
式中:γ为路段交通占有率;S为时段内路段上平均车辆数;a为标准车的长度,可取敞车、篷车和平车长度的平均值;L为路段长度。
通常情况下,城市交通网络在固定时期(一年或几个月)内几何线形不会发生重大的变化,交通需求情况较稳定或变化缓慢,可以大致认为日常交通流的时空分布也比较稳定,从而各路段上交通流的几何线形可视为固定的[16]。分别将S和W视为关于t的函数,当所预测的时间距当前时刻较近时,利用泰勒公式可得公式为:
S(t)=S(t0)+S′(t0)Δt
(4)
W(t)=W(t0)+W′(t0)Δt
(5)
式中:S(t)和W(t)分别为所要预测时段内车辆数和预测时段内交通流量值(机动车、非机动车和行人);S(t0)和W(t0)分别为车辆通过时段路段上的车辆数和交通流量值;S′0(t0)为过去几天同一时段内车辆数平均值;W′0(t0)为过去几天同一时段内交通流量值;Δt为所要预测的时段距车辆通过时段的时间间隔。
1.1.1 路段行驶时间
路段行驶时间是指货车从货运场站装货出发到周转返回货运站未发生堵车所耗费的时间T1,文中为车辆来回时间,认为来回行驶时间相同,可以用式(6)表示:
(6)
式中:T1为路段行驶时间;L为路段长度;V为货车行驶的平均速度。
1.1.2 交叉口延误时间
交叉口延误时间是由于交叉口交通流量过大,发生意外交通事故和天气原因等的影响导致车辆在交叉口逗留所耗费的时间T2。延误时间包括去时和回时两部分延误时间,可以用式(7)表示:
T2=S1Δt+S2Δt
(7)
式中:Δt为抽样时间间隔;S1为去时出口交通量;S2为回程出口交通量。
1.1.3 卸货时间
研究的卸货时间可以按照理想化处理,认为每种车型装卸同一种货物的时间是相同的。
1.2 货车周转及保养维修因素
公路货运场站车货配载研究需要考虑每次参与运输的车辆周转及保养维修因素,该因素会对运输任务产生影响。在进行车货调度时,参与运输任务出发以及需要保养维修的车辆会导致场站现有货车数量减少,而周转车辆以及完成维修保养车辆的返回又会使场站现有货车数量增加,进而对下一次运输任务的车货调度带来影响。这时候就需要货运场站提前调整运输计划,合理进行货车资源分配。
1.3 动态配载基本思想
公路货运场站的车辆与所需要运送的货物都是动态变化的。货运场站的货车数量可能会由于临时的抽调或者车辆的周转返回而有所变化,甚至包括车辆所出现的维修保养等因素都会对其产生影响,而货运场站的货物由于每批车辆的运送也会发生改变。这两者的不断变化意味着车货配载并不是一个一次优化,而是一个多次优化的动态过程。场站车辆的变化会影响对于货物的配载方案,货物经过每次装车后的变化又会影响到货运场站对于不同车型和数量的需求,两者之间是一个相互影响、相互反馈的关系。
2 车货动态配载优化模型
2.1 问题描述
货运场站通常有不同种类的货物等待运输,场站不同时刻分批次派出不同类型的车辆进行配载运输任务,不同类型的货车对于所装取的货物有各自的技术定额要求。在订单已下达,需要满足货运要求的情况下,同时考虑到周转车辆的返回以及货车保养维修等因素,如何进行动态调度研究使得所需的车辆数最少,优化车辆资源配置是笔者主要研究的问题。
通过应用车辆周转行程时间的预测结果,推测出未来时刻周转返回公路货运场站的车辆类型和数量,并建立了动态车货配载模型,以车辆数最小为目标函数,合理分配不同批次货车所装运的货物数量,以减少货车资源浪费,提高场站运作效率和经济效益。
2.2 问题假设
1)参与运输任务的货车为货运场站自备车辆,不需要运输公司参与。
2)卸货时间按照理想化处理,认为每种车型装卸同一种货物的时间是相同的。
3)不考虑货运场站堆场空间和装卸约束限制,即认为每批货车同时开始装卸和运输任务,不需要等待。
4)周转返回的货车如果遇到突发状况例如保养维修等因素无法参与下一阶段运输任务,会进行修理并等待下一阶段运输任务结束后重新加入。
5)不考虑货车在运输途中所发生的突发故障或事故。
2.3 模型建立
2.3.1 目标函数
本模型以车辆数最小为目标函数,该模型可以用公式表示为:
(8)
式中:m为货车车型数;n为货物种类;t为派出车辆的累计批次;xijk为第k批i型货车运送j种货物的车辆数。
2.3.2 约束条件
(9)
(10)
0≤wijk≤1 (∀i∈1,2,…,m∀j∈1,2,…,n
∀k∈1,2,…,t)
(11)
(12)
Ai(k+1)≤dik(∀i∈1,2,…,m∀k∈1,2,…,t)
(13)
T1k+T2ki≤T3ki(∀i∈1,2,…,m∀k∈1,2,…,t)
(14)
Arik+gi(k+1)-Ai(k+1)=Ari(k+1)
(∀i∈1,2,…,m∀k∈1,2,…,t)
(15)
(16)
(17)
(18)
(19)
(20)
xijk≥0,pij≥0,Aik≥0,Qik≥0,dik≥0
(21)
式中:Ai为货运场站所拥有的i型货车的初始数量;Aik为第k批发出的i型货车的数量;Arik为第k批货车发出后i型车的剩余数量;Qj为j种货物的初始数量;Qjk为第k批车辆装运前j种货物的剩余数量;pij为i型车装运第j种货物的技术定额;wijk为第k批i型车辆运送j货物的实载率;dik为第k批车辆运走后重新规划下一批i型货车的需求量;gik为第k批任务开始前由于周转车辆的返回或保养维修等因素引起i型车数量的变化值;T1k为第k批任务开始时间;T2ki为第k批车辆i在货运场站的装货与周转行程时间的总和;T3ki为第k批车辆i返回货运场站后距离最近的下次任务开始时间。
在上述模型中:式(8)为目标函数,求得所有批次车辆运送完全部货物所需的车辆数最小值;式(9)为每批次货车运送的货物类型不得超过该货物所剩余的最大值;式(10)为保证所有货物都被装运;式(11)为货车的实载率约束,不可以超载运输;式(12)为每批次发出的货车都被安排进行货物运输;式(13)为货运场站每批次发车的各车型数量不得大于上一批结束后计算所得出的剩余货物所需各车型的数量;式(14)为车辆周转行程时间约束,表示周转返回的车辆会加入下一次运输任务的调度中;式(15)为货运场站第k批剩余车辆与第(k+1)批剩余车辆之间的变化关系;式(16)为装运完全部货物所需的车辆数不得超过货运场站所提供的总车辆数,总车辆数会受到周转车辆返回以及车辆保养维修等因素的影响;式(17)为根据货车的车型有些货物无法进行装运;式(18)为优先度高的货物优先进行装运;式(19)和式(20)为决策变量;式(21)表示这些变量为非负整数。
3 算法设计
解乘数法是列奥尼德·康托罗维奇于1938年第一次提出,用于求解线性规划的方法,比1947年George Dantzig所发明的单纯形法早了将近10年。解乘数法为合理地组织生产和计划方式提供了开阔的应用前景,被广泛应用于有效地组织货物运输,合理分配机器作业等问题中。将解乘数法应用于车货配载问题中,确定初始方案,并且通过一系列变化规则来改变配载方案,对于一个实例,由于其基本可行解是有限的,所以最终可以得到该问题的最优解。采用解乘数法来对该模型进行求解,动态优化每批车辆运送的货物,具体的步骤如图1。
步骤1确定初始方案
对于每一种货物,选取技术定额p最大的货车进行分配,如果该类型货车全部分配完后仍有货物,则选取技术定额第二大的货车,以此类推直到货物全部分配完成。
步骤2计算剩余、不足行
计算货运场站内每一种车型的剩余、不足行。剩余、不足行等于现有各类车型的车辆数减去已分配的车辆数,其值为正属于剩余行,其值为负属于不足行。如果差值为0则分为两种情况讨论,如果该车型对于某种货物的技术定额与其它属于不足行的车型的技术定额相同,且该不足行车型已经分配了此种货物,则该车型为不足行,否则为剩余行。如果所有行都为剩余行,就说明此方案已达到最优,如果有不足行则代表还需要继续优化。达到最优后跳转到第7步,货物全部装运完成则结束。
步骤3计算解乘数值
每种货物的解乘数值r等于各个车型属于不足行的最大技术定额除以属于剩余行的最大技术定额。如果属于不足行的货车对该种货物没有分配,则不必计算r,在所有r中选出最小的值rmin。

图1 算法流程Fig. 1 Algorithm flow
步骤4变换矩阵
如果剩余行的数量大于不足行的数量,就用不足行的各个技术定额除以rmin,代替原来p值;反之,则用剩余行的各个技术定额乘以rmin,代替原来p值。
步骤5调整配载
将rmin中属于不足行,且已经分配的货物的全部(或部分)转移给属于剩余行且技术定额最大的货车,使得车辆不足的问题得以消除。
步骤6对调整过后的配载方案,重复步骤2~步骤5,直到得到最优方案。
步骤7根据前面解乘数法的优化结果,得出完成剩余货物所需的各个车型以及对应车辆数。场站根据自身情况进行安排,决定下一批次进行运输任务的车型和数量。
步骤8货车根据货物优先度进行装运,货物优先度由场站根据客户要求以及自身情况所决定。装运并发车后,计算场站内剩余货物量,以及在下一批车辆调度计划制定之前,周转车辆的返回以及保养维修所造成的货车数量变化。最后跳转到步骤1,对下一批车货配载进行优化。
其中,步骤1~步骤6是解乘数法对于一次车货配装的优化求解过程。通过步骤7、步骤8,调整每次配货后车辆以及货物的变化参数,将一次配装过程进行循环往复,进而实现了基于解乘数法的动态车货配载优化。
4 算例分析
4.1 算例描述
为了检验模型和算法的有效性,笔者给出算例分析。大连某货运场站到目的地距离为4 km,所有发往目的地的车辆都沿一条道路行驶,货车以平均36 km/h车速自由行驶,交叉口堵车距离大约为200 m。货运场站待运货物种类和吨数,车种数量以及技术定额如表1。货物运送优先度根据客户需求决定,为钢材>水泥>混凝土>花岗岩>大理石>瓷砖,货运场站的货车在技术定额允许的情况下,按照优先度顺序进行装运。场站共计发车6批完成所有运输任务,每批出发的车辆类型和数量由货运场站根据每次解乘数法求解得出的需要车辆数进行安排,具体见表3~表8。车辆周转行程时间预测如表2,装卸时间为车辆在货运场站的装货时间和到达目的地的卸货时间的总和。

表1 车辆技术定额Table 1 Vehicle technical quota

表2 车辆行程时间预测Table 2 Vehicle travel time prediction
4.2 结果分析
根据上述车货以及车辆行程时间预测数据进行动态配载优化,用MATLAB软件根据模型进行编程计算,每一阶段优化结果如表3~表8。其中第1列剩余车数用“a+b-c+d”的形式来表示,a为货运场站发车后的剩余车数,b为下一批任务开始前周转返回的车辆,c为因故障需要保养维修的车辆数,d为之前保养维修后返回的车辆数,每种货物所需的车辆数及运送吨数用“e/f”的形式来表示。

表3 第1批车货配载优化Table 3 First batch vehicle-cargo stowage optimization

表4 第2批车货配载优化Table 4 Second batch vehicle-cargo stowage optimization

表5 第3批车货配载优化Table 5 Third batch vehicle-cargo stowage optimization

表6 第4批车货配载优化Table 6 Fourth batch vehicle-cargo stowage optimization

表7 第5批车货配载优化Table 7 Fifth batch vehicle-cargo stowage optimization

表8 第6批车货配载优化Table 8 Sixth batch vehicle-cargo stowage optimization
在相同算例的情况下,用静态解乘数法来对该问题进行求解,不考虑货运场站车辆周转返回以及车辆数在中途受到其他因素影响而改变,结果如表9。

表9 静态解乘数法求解结果Table 9 The result of static solution multiplier method
将静态配载与动态配载所需要的总车辆数进行比较,结果如表10。
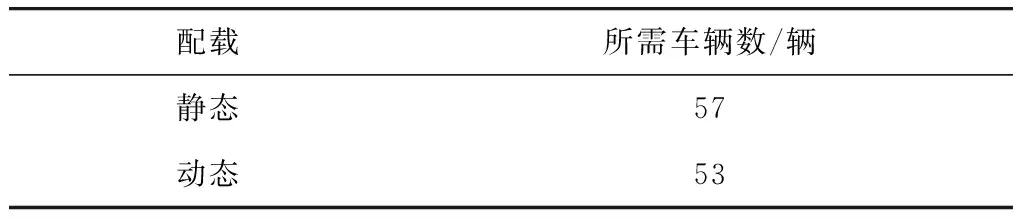
表10 静态配载与动态配载所需要的总车辆数Table 10 Total number of vehicles required for static anddynamic stowage
从表10中可以看出,通过动态车货配载优化后得出的结果更优,后者考虑到了运输周转返回的车辆对配载优化的影响,可以更好的应对车辆维修保养的情况,对于车货的动态变化做出更为灵活的反应,同时减少货车资源浪费,使得货运场站可以将剩余的货车资源投入到其他运输任务中,提高场站的经济效益。
5 结 语
对货运场站货车周转的行程时间做了预测,使货运场站能够及时掌握货车运输周转返回时间,进行相应的车辆调度和货物装运准备。针对公路货运场站车货的配载问题建立了数学模型,考虑到了周转车辆返回后引起的车辆数变化,以及返回车辆可能进行维修保养暂时无法开展运输任务而带来的影响,通过动态解乘数法求解。算例结果表明该模型是有效的,可以更好地适应车辆与货物的动态变化过程,节约货车资源,合理优化货车资源配置,进而为场站其它运输任务提供便利,提高货运场站的经济效益和运作效率,为实际中的场站车货配载提供理论参考依据和实际应用价值。

