考虑交叉口延误的交通微循环路网优化研究
张丽莉,高雪溢
(东北林业大学 交通学院,黑龙江 哈尔滨 150000)
0 引 言
当下我国交通拥堵问题日益严重,且多发在干路路段,单纯新修道路不仅工程造价高,且会诱发新的交通需求,于是有学者提出交通微循环理论。交通微循环理论将现有城市支路、甚至小区内部更窄小的道路转化为微循环道路,当干路发生交通拥挤时,车流自干路分流进入微循环路网,再通过路径选择,由微循环道路最后又回到干路,利用现存道路基础设施,有效分流干路的交通需求,提高路网整体交通承载力。国内外针对城市交通微循环的研究主要分为两个方面:①对交通微循环基本原理的研究:C.P. MICHAEL[1]分析了小区域内的交通微循环系统,指出提高路网支路密度,能有效提高路网可达性,交通微循环系统所能发挥的效益大小也与支路网密度成正比;W.CHRISTOPHER等[2]研究得出,进行交通微循环组织优化设计能有效减缓交通拥堵,并以交通微循环系统特征为依据,提出特殊的交通微循环空间组织模式;②基于交通微循环理论进行路网优化:陈群等[3]在考虑出行者行为选择的基础上,以支路通行能力为约束,对交通微循环网络中各种交通组织方式进行了一体化决策;罗清玉等[4],王秋平等[5],史峰等[6]构建了交通微循环路网优化设计模型,通过组织交通微循环改善街区交通情况。然而,车辆在路网上行驶所产生的总延误中,交叉口延误所占比例高达80%,但大多数已构建的交通微循环理论模型缺少对交叉口的分析。为此,笔者考虑交叉口对路网延误的影响,基于交通微循环理论建立双层规划模型,对拟规划区域设置微循环系统,期望规划区域内路网运行效益最佳。
1 模型建立
构建交通微循环系统,必须要解决微循环道路选择和已选择道路改造深度2个问题。针对这2个问题,笔者建立了考虑交叉口延误的交通微循环路网优化双层模型,该模型由一个上层模型和一个下层模型组合而成。上层模型以路网平均行程速度最大为目标,以路段饱和度、通行能力和投资额度为约束条件,建立非线性约束模型,从备选道路中选择构成交通微循环系统的道路,并确定选取道路的改建程度;下层模型将交叉口延误与路段行驶时间结合,构造阻抗函数,并以路网总阻抗为目标函数,在满足上层模型约束条件的前提下,进行路网交通平衡分配。
上层模型的决策变量为备选道路集中各道路改造后通行能力,下层模型的决策变量为各出行者路径选择。上层模型管理者在选择决策变量的过程中,需要考虑上层模型目标函数和约束条件的影响,还需兼顾下层模型出行需求最优解的制约,所选择的决策变量还会影响下层模型出行者的行为选择[7];同时,下层问题出行者路径选择的决策也受上层模型约束条件的约束。通过多次管理者决策与出行者行为选择,使上下层目标函数均得到最优解,此时路网运行效率最佳。
1.1 路网预处理
设定拟规划区域路网G=[E,A∪B]。其中,E为规划区域内所有交叉口构成的集合,即节点集;A为周边干道所组成的集合,即现有干路集;B为备选道路集,包含根据道路通行条件、道路功能选出的满足组织交通微循环条件的支路、等级以下道路及断头路。
1.2 上层模型
1.2.1 目标函数
交通微循改造的目标,是通过布设交通微循环系统,使部分交通需求通过交通微循环路网穿越,躲避拥堵干路,提高路网运营效益。参考《美国通行能力手册》,笔者以路网平均行程速度作为上层模型的目标函数,如式(1):
(1)
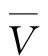
1.2.2 约束条件
1)饱和度要求
若某一地点的交通需求超过其通行能力,用平均行程速度衡量路网的运行效率就失去了作用。因此,改造后各路段饱和度需小于1,如式(2):
(2)
式中:S为分析路段饱和度;N为改造后分析路段上的交通量,veh;X为改造后分析路段的通行能力,pcu/h 。
2)通行能力要求
各备选道路改造程度需满足其改造能力要求如式(3):
Cb≤Xb≤Cmax
(3)
式中:Xb为改造后备选道路b的通行能力,pcu/h;Cb为改造前备选道路b的通行能力,pcu/h;Cmax为备选道路b的通行能力上限,pcu/h。
3)投资额度要求
在进行城市交通微循环路网改造时,需要对改造费用进行严格把控,改造总费用不得超过预设的投资额度,如式(4):
0≤Z≤Zmax
(4)
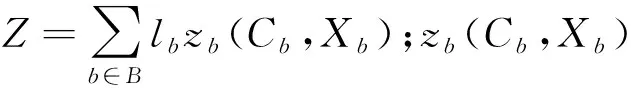
1.3 构建下层模型
根据上层模型生成的决策,可以确定改造后路网联通情况。结合改造后路网联通情况,通过路阻函数,计算得到每对OD点对之间全部路径的初始路径阻抗。下层模型的决策者(出行者)选择初始路径阻抗最小的方式出行,进而实现OD交通量的初步分配。初步交通分配改变了路网中各路段上的交通量,使得各路径阻抗也随之发生变化。通过多次出行者行为选择,对出行者的出行阻抗进性调节,使两次交通分配的精度小于预设值,得到交通分配最优解。
1.3.1 构建路阻函数
车辆在路段上的行程时间由在路段上的行驶时间R和该路段对应交叉口e的入口道延误De组成[8]。以车辆在路段上的行程时间为路段阻抗,则路阻函数t=R+De
车辆在路段上的行驶时间R通过BPR函数可以计算如式(5):
(5)
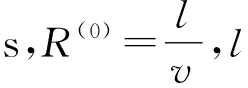
交通微循环路网所涉及的交叉口一般为无信号交叉口。当支路与主干路相交时,采用“支路只准右转通行”[9],此时主干路上的交通流不产生延误,支路上车辆的平均延误等于加、减速延误、反应延误及交织点延误之和,取经验值De=6.5 s。
当支路与次干路相交或支路与支路相交时,采用“减速让行或停车让行标志管制”[9],此时各入口道上车辆的平均延误如式(6)
(6)
式中:T为分析时段时间(例如:分析时段为15 min,T=0.25);Ce为分析路段对应交叉口e的入口道通行能力,pcu/h。
1.3.2 目标函数
下层模型的目标函数[10]如式(7):
(7)
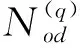
1.3.3 约束条件
1)路段流量守恒条件
每条路段上的交通量都应等于使用该路段的路径流量之和,如式(8):
(8)
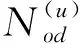
2)流量非负条件
2 模型求解算法
鉴于双层规划模型的复杂性,通过遗传算法建立模型求解算法,步骤如下:
步骤1初始化。对遗传算法运行参数进行赋值,参数具体包括终止进化代数gm、变异概率Pm、交叉概率Pc以及种群规模β。并输入设计速度、道路通行能力、交叉口通行能力等参数。
步骤2编码。将备选道路集中各路段改造程度转换成一组变量fb,b∈B即模型的决策变量。若备选道路b未被选择,则fb=0;若备选道路b被选择但改造后通行能力不变,有Xb=Cb,则fb=1;若备选道路b被选择且改造后通行能力提高kσ,有Xb=Cb+kσ,其中,σ为单车道通行能力,则fb=k+1。对决策变量fb,b∈B进行实数编码。
步骤3初始种群生成。随机产生β个初始编码串,即β个初始个体,构成初始种群。
步骤4交通分配。将现有种群代入下层模型,通过路阻函数,计算得到各路段阻抗,进行交通分配,求解出各路段交通量。
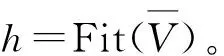
步骤6选择。采用轮盘赌法,选择下一代种群,形成新种群。
步骤7交叉。以Pc概率对选择后形成的种群执行交叉算子,形成新种群。
步骤8变异。以Pm概率对交叉后形成的种群执行变异算子,形成新种群。
步骤9终止判断。判断是否达到终止进化代数gm,若达到,则输出最佳个体,否则,转向步骤4,循环直至达到终止进化代数gm。
3 实例分析
选取黑龙江省大庆市高新技术产业开发区新玛特地区为例,其路网现状如图1。
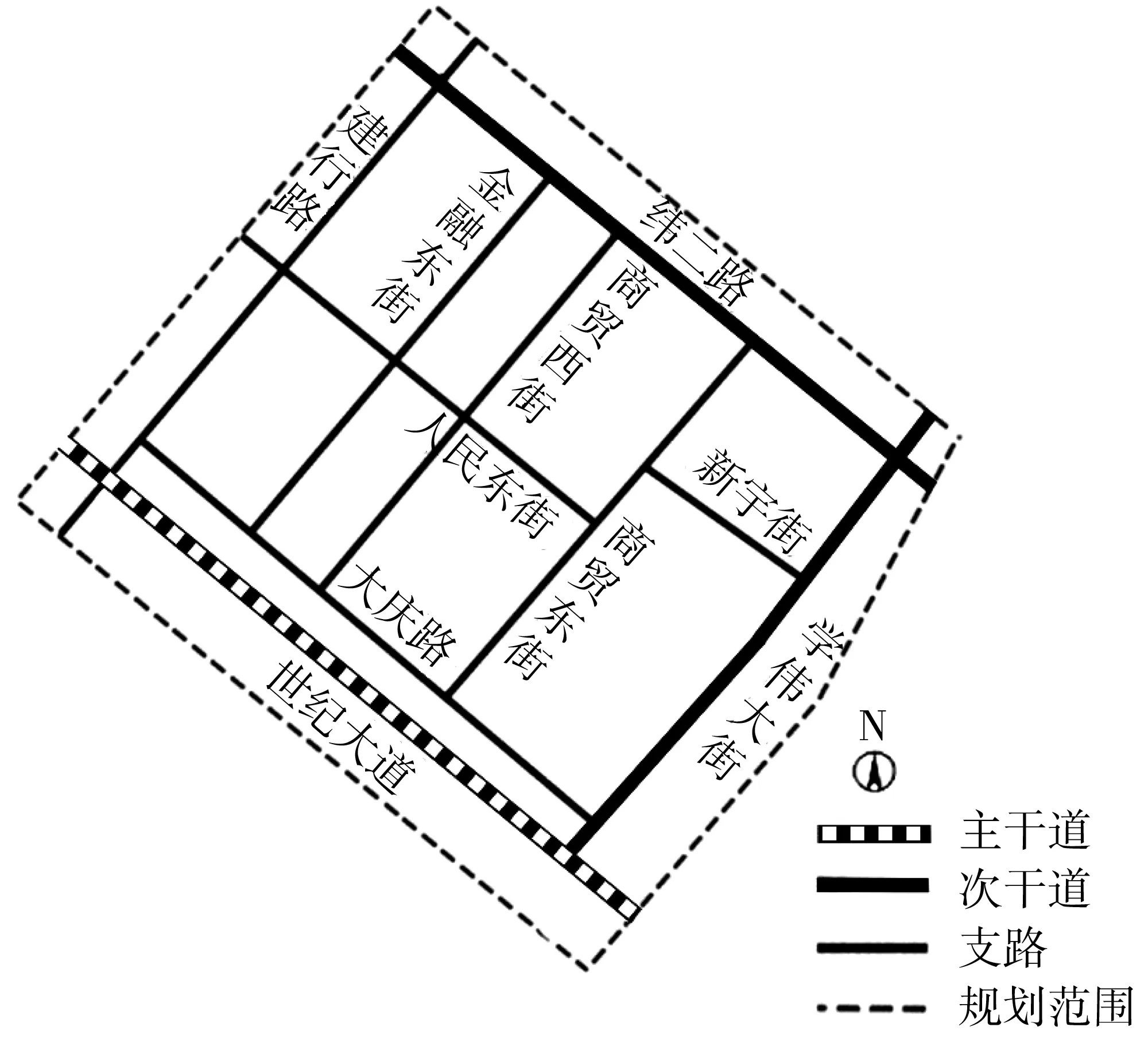
图1 路网现状Fig. 1 Status of road network
根据道路通行条件、主要功能对规划区域内干路、支路、等级以下道路及断头路进行筛选,选择满足设置交通微循环条件的道路,构成可利用的道路网络结构如图2。筛选后得出:现有干路集A包含世纪大道、纬二路、学伟大街3条道路。备选道路集B包含建行街、商贸西街、商贸东街、金融东街、新宇路、大庆路、人民东街、以及4条等级以下道路(路段8—12、10—11、13—21、9—26)和1条断头路(路段20-5)。
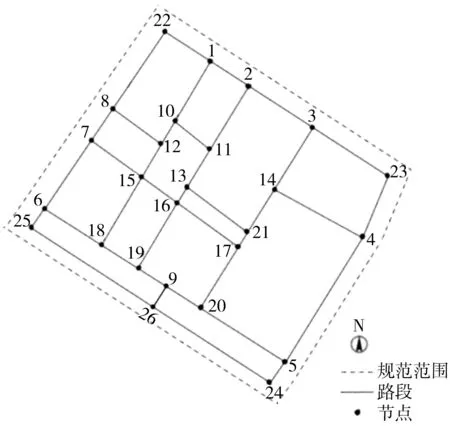
图2 规划路网结构Fig. 2 Planning road network structure
确定规划区域内路段、交叉口的各项参数取值标准。由于交通微循环路网优化是路网规划分析的一部分,主要以假设特征为基础,分析时间往往是长期的,缺乏规划后的实测数据,道路参数采取默认值或估计值如表1。无信号交叉口通行能力,在减速让行时取1 100~1 580 pcu/h,停车让行时取970~1 560 pcu/h,受道路、交通、环境等条件影响较大的路段或交叉口,可根据实际情况,设置折减系数调整其通行能力。
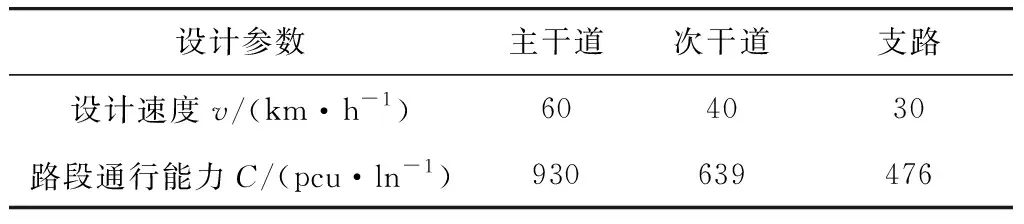
表1 道路参数Table 1 Road parameters
规划区域内各备选道路属性如表2。
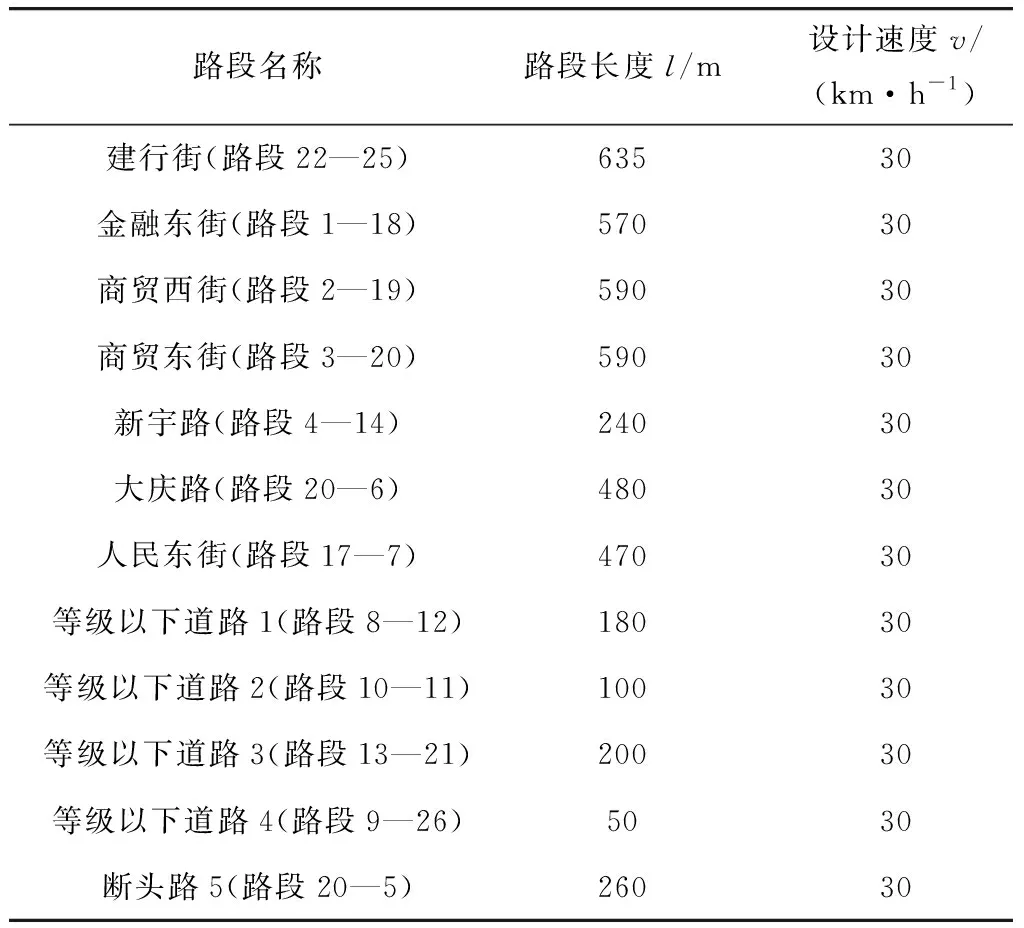
表2 备选道路属性Table 2 Alternative road properties
现有支路、等级以下道路的改造费用为每公里71.7万元/车道,断头路的改造费用为每公里336.5万元/车道[7]。
使用MATLAB编写遗传算法程序,进行问题求解,具体程序设计如下:
步骤1道路网络数字化。采用邻接矩阵法对规划路网情况编码录入。其中,邻接矩阵distance中非零元素表示两节点(两节点数对应该元素行数-列数)间连通且元素值等于连接边长度。
步骤2编码。备选道路集B中共有11条路段通行能力可变,各路段通行能力改造深度决策变量fb可取值{0,1,2,3},采用二进制编码,则个体chromlength长度取22。
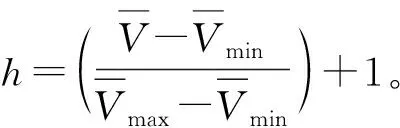
步骤4初始化。设置终止进化代数gm=100,变异概率Pm=0.05,交叉概率Pc=0.7,种群规模β=20。
步骤5设置OD交通量矩阵。
步骤6随机生成一个种群规模为50,个体长度为22的初始种群。
步骤7进入进化迭代循环。
步骤8设定转码规则。将当前种群转码至上层模型决策变量,并结合上层模型决策变量,根据提前预设的不同等级路段及交叉口参数,按顺序给路段设计速度矩阵V、路段通行能力矩阵Cmax、交叉口通行能力矩阵CmaxS三者赋值;
步骤9进行交通分配。返回交通分配矩阵N,阻抗矩阵t以及交通分配精度α。
步骤10判断是否满足约束条件。
步骤11计算种群中每个个体的适应度,并选择出群体中最大的适应值及其个体。
步骤12执行选择、交叉、变异算子。
步骤13循环终止判断。
通过程序运行计算得到遗传算法迭代曲线如图3。
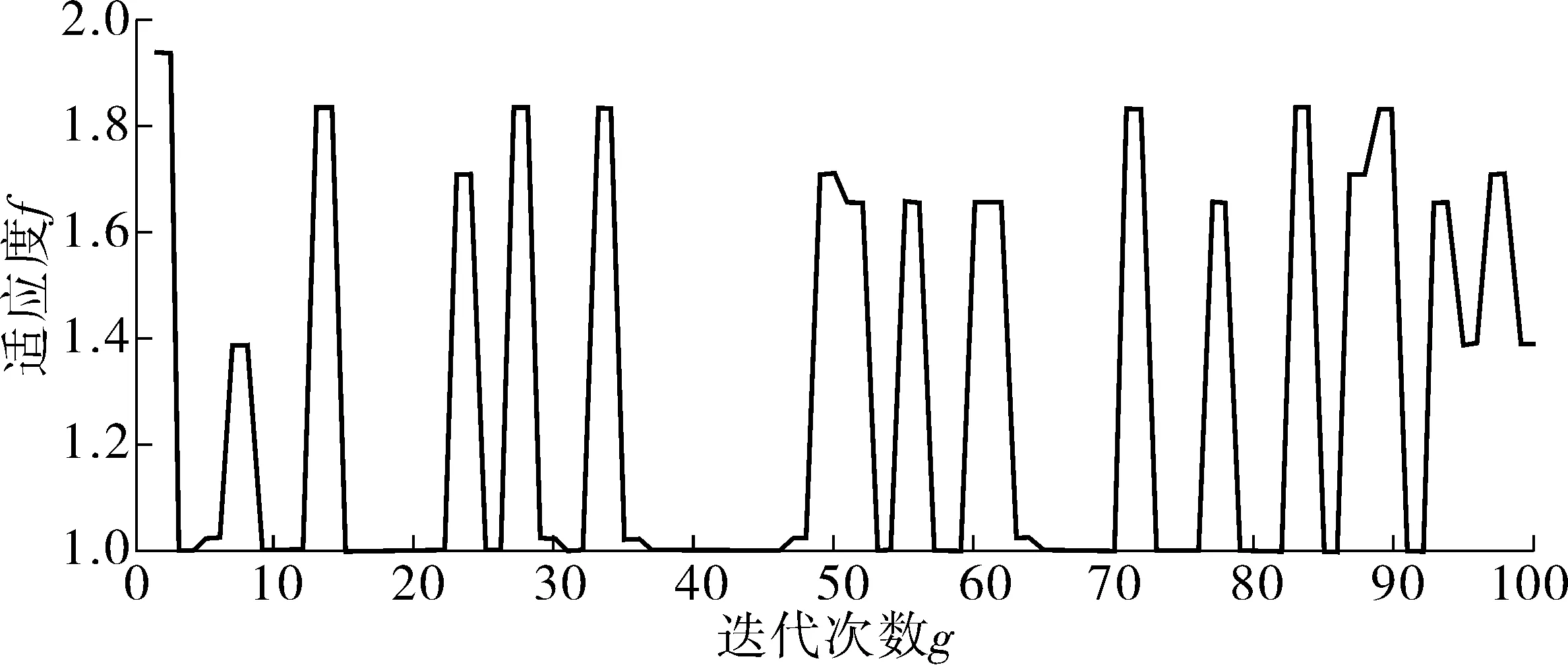
图3 遗传算法迭代曲线Fig. 3 Iteration curve of genetic algorithm
通过程序运行得到最大适应度个体chromlength=[1 0 0 1 0 1 1 0 1 0 1 0 1 0 0 0 1 0 0 0 0 0 ],根据该结果及其表示含义,可得到最佳改造方案如下:人民东路、大庆路、新宇路拓宽至双向四车道,等级以下道路1、3(路段8-12、路段13-21)改建成双向两车道支路,与现有道路(世纪大道、纬二路、学伟大街、建行街、商贸西街、商贸东街、金融东街)构成微循环路网。
对比分析优化前和优化后路网的各路段饱和度,如图4。
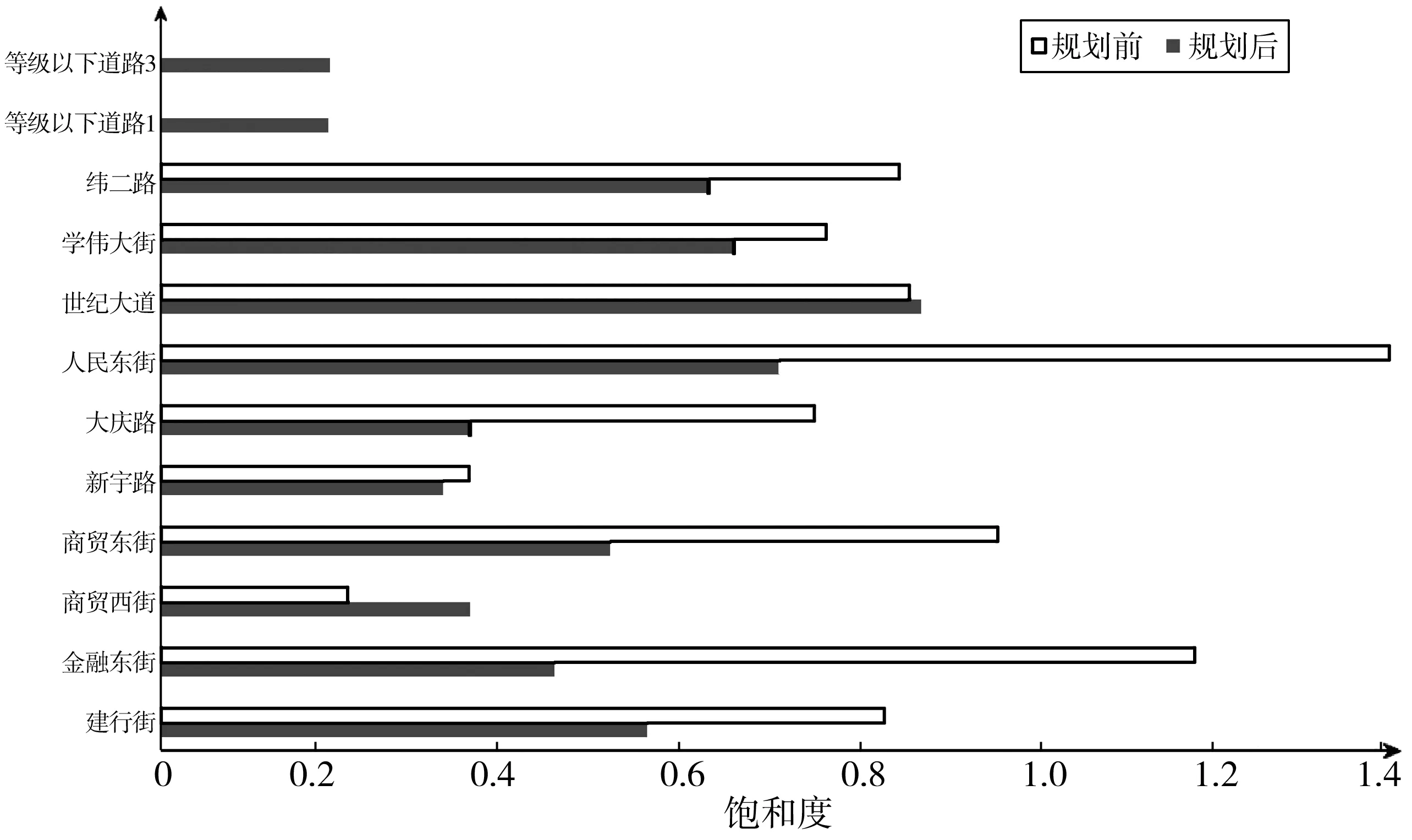
图4 优化前和优化后各路段饱和度Fig. 4 Saturation of each road segment before and afteroptimization
对比分析可知,优化前饱和度大于0.90的道路有3条,干路平均饱和度高达0.72,路网平均饱和度也达到0.65;优化后各道路饱和度均小于0.90,干路平均饱和度降低至0.65,路网平均饱和度仅0.43。交通微循环系统设置后,有效降低干路饱和度,提高支路利用率,均衡干路与支路之间的交通量,证明该模型具有有效性。
4 结 语
1)交通微循环理论主要利用现有支路资源,分流干路交通,在合理规划和设计的前提下,解决区域交通拥堵问题。
2)笔者重点讨论了交通微循环理论在路网优化方面的应用,建立了考虑交叉口延误的交通微循环路网优化双层模型,上层模型用以解决如何在投资额度允许的范围内提高路网运营效益的问题,下层模型考虑路网的改变对出行者路径选择的影响。并通过实例验证本文所提出模型和算法的合理性,验证结果表明:干路平均饱和度高由0.72降低至0.65,路网平均饱和度由0.65降低至0.43,所提出的模型具有有效性。

