基于衰减路径时变性的压力容器疲劳裂纹安全裕度研究

谢 阳, 赵 波, 龙 伟, 刘华国, 李炎炎

(1. 四川大学机械工程学院, 成都 610065; 2. 先进制造技术四川省重点实验室, 成都 610065)

1 引 言

随着我国迈入中国制造2025计划，压力容器作为关乎经济发展的特种储存设备，其重要性越来越明显，尤其在石油天然气工程、核动力工程、化工工程和空气动力学试验等国家重点工程项目中被广泛使用.大型压力容器在生产制造和环境介质等外部条件影响下，其表面和内部会存在各种先天性或后发性缺陷，如凹坑、夹渣、裂纹、未焊透等.调查发现，引起这些事故最主要的缺陷形式是裂纹[1-2].传统方法对于压力容器安全程度的评估是在考虑弹性断裂和塑性失稳的基础上，形成双判据失效评定图(Failure Assessment Diagram, FAD)[3].对于安全程度的计算为“射线法”，但是射线法只能从静态的角度出发，判断裂纹缺陷静态的剩余安全裕度大小，无法表征裂纹扩展过程中的时变性对含裂纹缺陷下的动态安全裕度[4].本文的主要研究目的是通过对不同类型的裂纹在扩展过程中裂纹几何形态变化的研究，得出不同裂纹类型下的安全衰减路径，建立含缺陷压力容器在不同裂纹初始尺寸下的动态安全裕度表征模型;从而解决传统安全裕度计算方法无法实时表征安全裕度大小的缺点，为含缺陷压力容器的安全裕度评定提供新的思路.

2 裂纹的扩展规律及关联函数

不同类型的裂纹在扩展过程中裂纹几何形态变化影响着安全衰减路径的建立，进而影响含缺陷压力容器在不同初始裂纹尺寸下，动态安全裕度表征的准确性，所以对于裂纹扩展规律的探究十分必要.

2.1 裂纹扩展规律准则

根据大型压力容器构造特点，其曲率很小，可以忽略不计. 将含裂纹处简化为如图1所示受均匀张力的平板进行研究[5].计算时将表面裂纹和埋藏裂纹规则化为(半)圆形或(半)椭圆形.

图1 含埋藏裂纹的平板Fig.1 Flat plate with emdedded cracks

疲劳裂纹扩展主要是描述裂纹在疲劳载荷作用下的形状变化.不同类型的裂纹都遵循基于断裂力学理论及实验提出的疲劳裂纹扩展式[6-8]，即Paris公式:

(1)

式中ΔK为应力强度因子变化范围;C和m是与材料有关的参数, 通过试验测得,m取值2～7.

考虑到裂纹扩展存在“闭合效应”，Elber[9-10]最早发现该现象，同时，定义了裂纹闭合系数U并给出经验公式U=0.5+0.4R，Schijve[11]对公式进行修正如下：

U=0.55+0.35R+0.1R2

(2)

将式(2)代入式(1)，有：

(3)

利用Paris公式分别计算裂纹长度值c和深度值a与疲劳应力循环次数的积分关系.以埋藏裂纹为例，如图2，在计算中只考虑前端的中心裂纹处A和边界裂纹处B. 其数学表达式为：

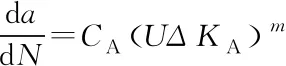
(4)

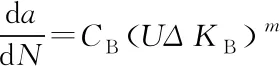
(5)

上两式中ΔKA、ΔKB分别为中心裂纹处A，边界裂纹处B的应力强度因子的变化范围；CA、CB分别为中心裂纹处A，边界裂纹处B的Paris公式常数.

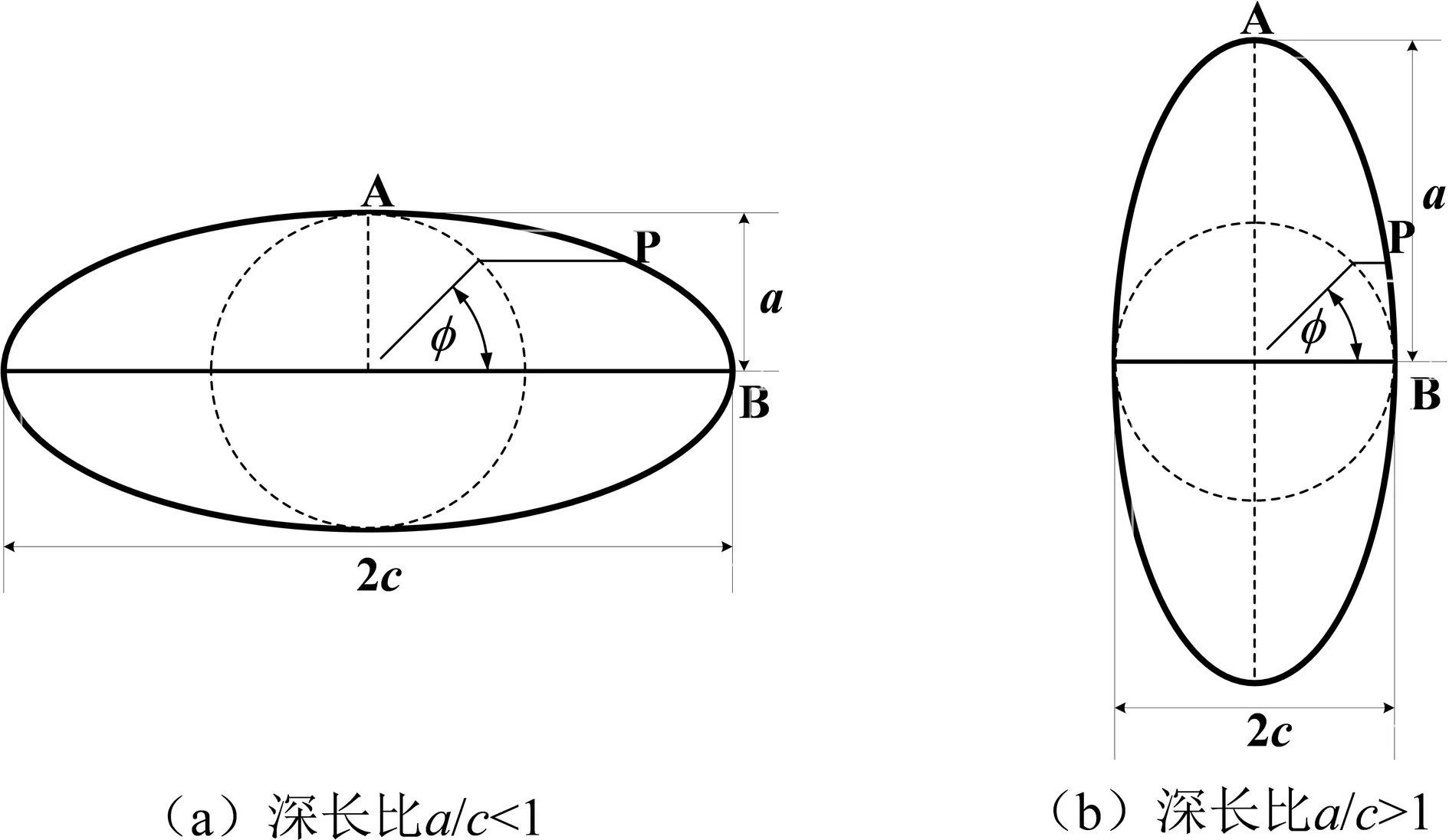
图2 埋藏裂纹初始形状Fig.2 The initial shape of the embedded crack

将式(4)和(5)进行数值迭代，能够获得关于裂纹缺陷深度值与长度值的关联关系：

(6)

从式(6)可知，裂纹在深度和长度方向上的关联关系，不仅与裂纹尖端处应力强度因子K，而且和材料常数C、m相关. 对于表面裂纹，其在裂纹长度方向上存在较大的塑性区，受表面的延展性阻碍作用[12]，在一定程度上将影响长度c的扩展，可以取CA=0.9mCB，针对埋藏裂纹而言，其不存在表面延展性作用取CA=CB. 因此，埋藏裂纹和表面裂纹通过以下方式扩展：

(7)

式中Δa(Δa→0)为裂纹中心处A点的扩展变化量；Δc为裂纹边界处B点的裂纹扩展变化量. 由式(7)可知，裂纹在深度和长度方向上的关联关系，主要与裂纹应力强度因子K有关，且式(7)可写成：

(8)

将式(8)分别进行迭加计算后，能得到裂纹扩展变化n次后的尺寸值，分别取裂纹初始深度和长度值为a0、c0，长度尺寸an、深度值cn，其表示式为：

an=a0+nΔa(n=1, 2, 3...)

(9)

(10)

2.2 应力强度因子的计算

大型压力容器埋藏裂纹所在部分假设成如图2所示的平板，分析位于平板的横截面区域所对称埋藏缺陷相关的裂纹路径，该缺陷受疲劳I型载荷下的均匀张力. 本文运用Newman和Raju[13-15]提供的计算埋藏裂纹和表面裂纹应力强度因子K的方法. 埋藏裂纹计算方程受拉应力下0≤a/c≤∞、c/b<0.5且-π≤φ≤π时有效，当取0≤a/c≤0.2，则有a/t<1.25(a/c+0.6)；当取0.2≤a/c≤∞，则有a/t<1；表面裂纹计算方程受拉应力作用下0≤a/c≤2、c/b<0.5和0≤φ≤π有效，当取0≤a/c≤0.2，则有a/t<1.25(a/c+0.6)；当取0.2≤a/c≤2，则有a/t<1，但两者对于a/t>0.8作者尚未给出确定的精度，其中a是裂纹深度值(mm)；b是裂纹所在平板长度的一半(mm)；c是裂纹长度的一半(mm)；t是裂纹所在平板厚度(mm).

埋藏裂纹应力强度因子Ke表达式如下:

(11)

表面裂纹应力强度因子Ks表达式如下:

(12)

公式中St为受到的拉力；Sb、Hs分别为受到的弯曲应力和弯曲修正系数；φ为裂纹扩展角度；Fs、Fe、Q为计算中的过程变化量, 和裂纹形状变化有关，具体推导过程见文献[14].

我们通过以上公式可以求解裂纹的应力强度因子K，进一步分析裂纹扩展的扩展变化情况.

2.3 裂纹扩展的数值分析与迭代计算

假设裂纹呈(半)圆形或(半)椭圆形，裂纹前沿裂纹点的扩展方向都垂直于裂纹前端方向，如图2.将椭圆形裂纹的前沿运用Simpson公式离散化分成长度相同的z段.并且每个裂纹点n都在垂直于裂纹前端方向上扩展并且遵循Paris公式，使裂纹的最大裂纹扩展量△amax在扩展变化过程中保持恒定，这样与椭圆形裂纹前沿上所有裂纹点都相关联，且最大裂纹扩展量对应存在最大应力强度因子△Kmax.根据Paris迭代计算公式(7)，得到如下公式，通过该公式可以求解椭圆形裂纹前沿上任意一点n的裂纹扩展量△an.

(13)

式中△an是第n点的裂纹扩展变化量，△amax是计算过程中最大裂纹扩展变化量，△Kn是第n点的应力强度因子变化，△Kmax是最大应力强度因子变化.基于Newman和Raju的方程(式(11)、(12))，有如下公式：

(14)

通过上式计算得到某一时刻下任意一点的裂纹变化量，利用最小二乘法进行拟合形成新的椭圆形裂纹前沿，进而可以得到不同时刻下裂纹扩展深度和长度的变化规律.同时利用Python语言将上述数值计算模型编程，分析裂纹路径变化规律，通过迭代计算得出裂纹深度和长度的变化曲线.通常裂纹形状变化通过裂纹的深长比a/c和相对裂纹深度a/t来表示，根据计算绘制了a/c随a/t的函数变化曲线.主要迭代流程如图3. 流程图中：Δai为深度方向第i次的裂纹扩展变化量；Δci为长度方向第i次的裂纹扩展变化量.

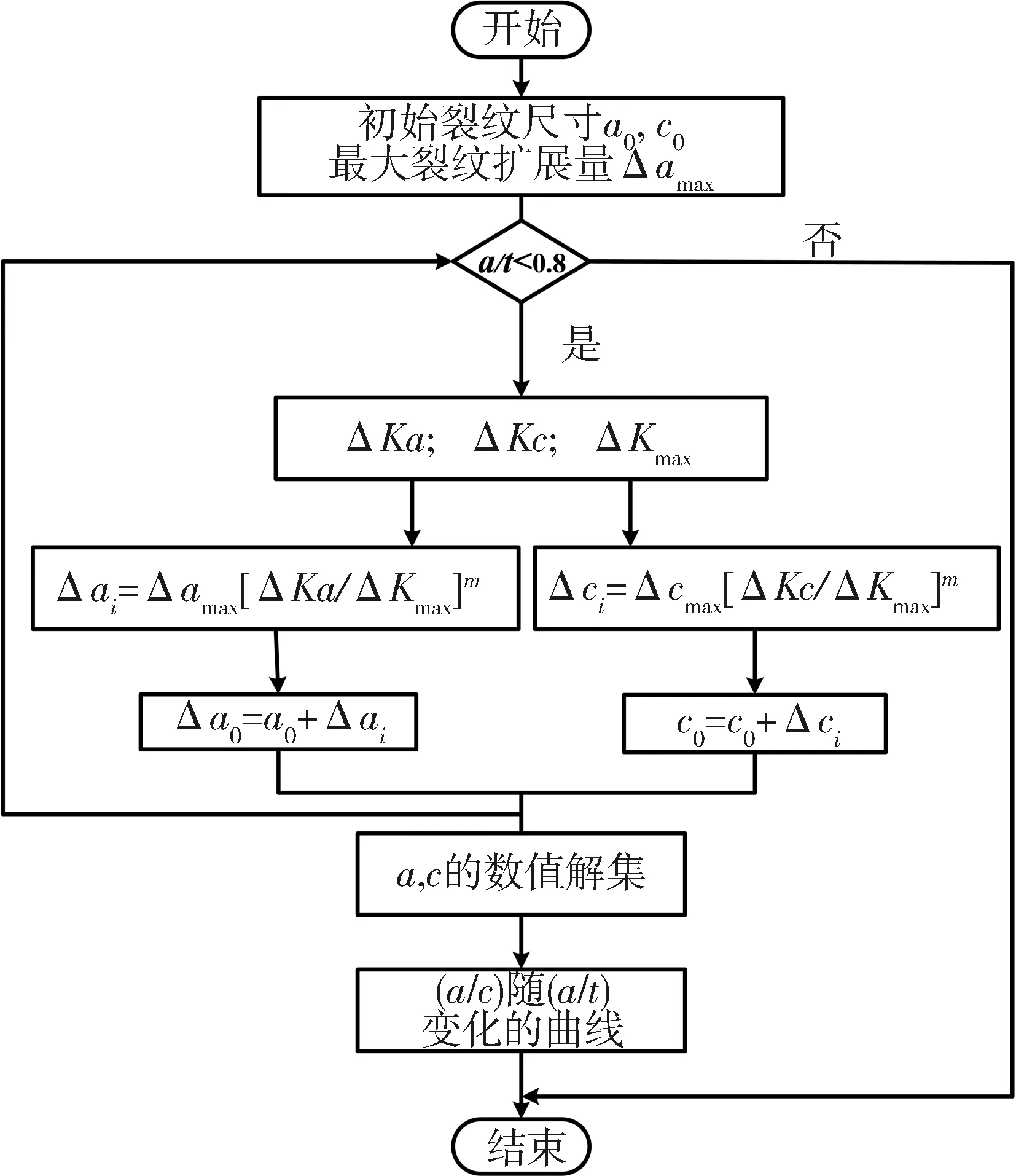
图3 迭代计算流程示意图

2.4 关联函数分析

首先运用Python语言对模型编程，收敛计算得到了数值结果，将埋藏裂纹和表面裂纹的裂纹前沿离散化为均匀长度的z段，令循环计算过程中裂纹最大深度变化值△amax=0.00001t，压力容器常用材料16MnR在Paris公式中材料相关系数m取值为2～4，这里取m=3.图4绘制了埋藏裂纹和表面裂纹在初始裂纹尺寸为(a/t)0={0.02, 0.2, 0.4}和(a/c)0={0.2, 0.5, 1.0, 1.5, 2.0}共15个初始裂纹尺寸不同的深长比(a/c)随相对裂纹深度(a/t)的函数变化情况.

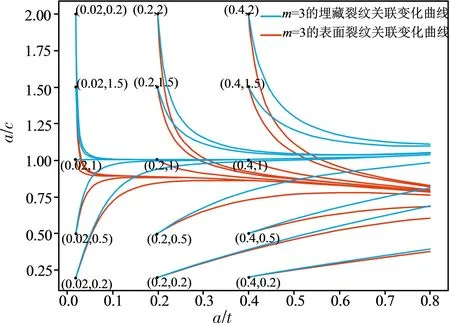
图4 表面裂纹和埋藏裂纹扩展变化对比图(线上彩色)

从图4分析可知：(1) 埋藏裂纹和表面裂纹受拉作用下，裂纹形状变化趋势相同，当(a/c)0<1时，裂纹深长比a/c随相对裂纹深度a/t增加而变大，靠近于1时趋于稳定；当(a/c)0>1时，裂纹深长比a/c随相对裂纹深度a/t增加而变小，靠近于1时趋于稳定，表明两种裂纹受拉伸应力作用时，最后的形状变化趋向于近似a=c的方向发展.将图4中两种裂纹所有曲线分别收敛于某一趋势的路径定义为“最优扩展路径”，表面裂纹的“最优扩展路径”比埋藏裂纹更低.(2) 对于相同类型的裂纹，初始裂纹相对裂纹深度(a/t)0一定时，初始深长比(a/c)0的值越大，曲线会更快收敛于最优扩展路径；当(a/t)0≥0.2受到拉应力时，曲线会更慢收敛于最优扩展路径.(3) 对于不同类型的裂纹，表面裂纹比埋藏裂纹曲线更快收敛于最优扩展路径.

选取图4中部分不同的初始裂纹点所形成的曲线进行曲线拟合，生成表1和表2的裂纹关联函数.

表1 埋藏裂纹深度a和长度c变化关联函数

表2 表面裂纹深度a和长度c变化关联函数

将本文提出的数值计算模型进一步验证，在相应工况下运用数值模型计算文献[16-17]裂纹初始值下变化趋势与文献实验值比较，即使考虑到工程材料中疲劳裂纹扩展的固有实验误差，模型预测和实验结果之间的一致性也非常好.

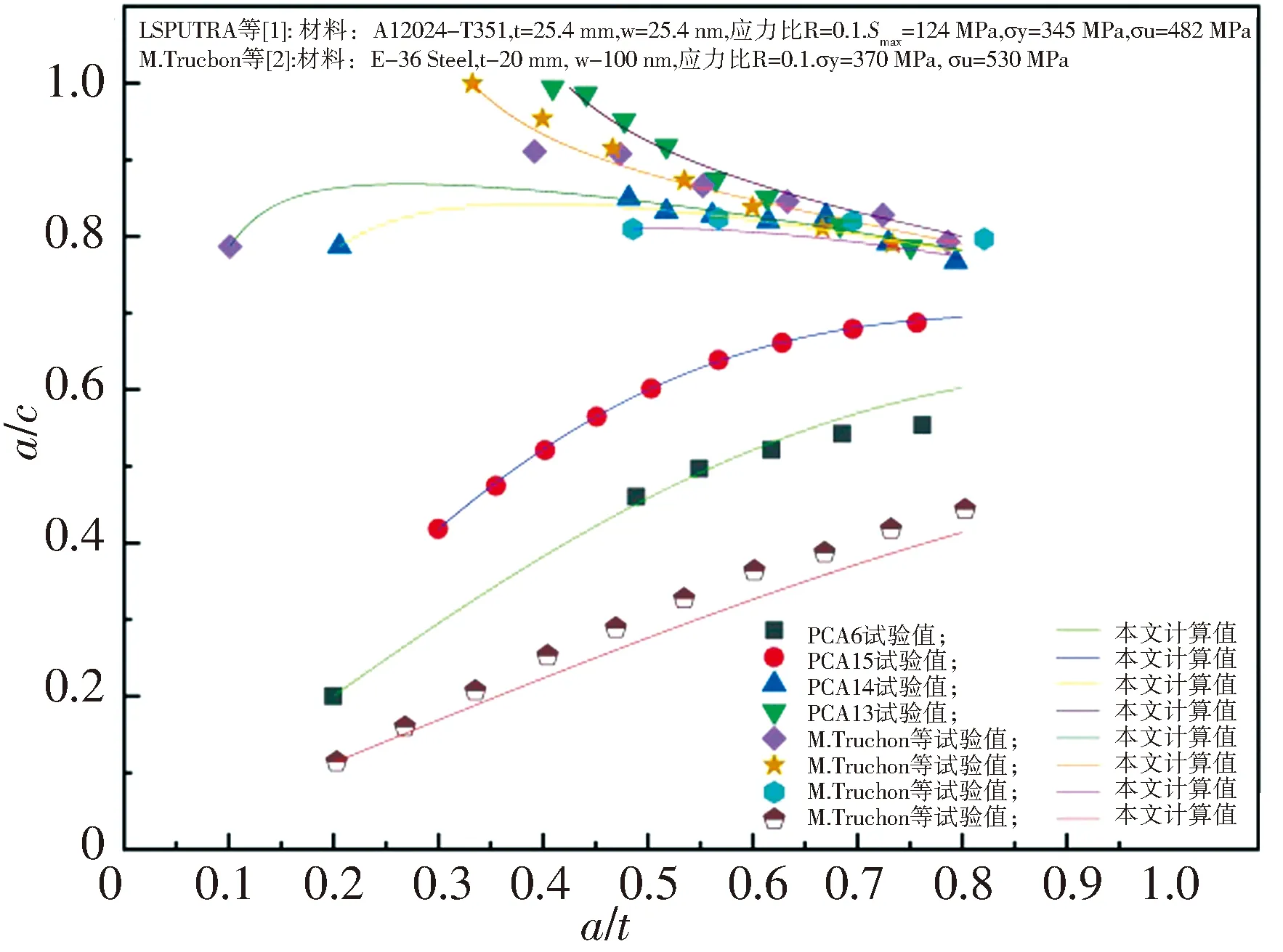
图5 表面裂纹模型计算值与实验值对比(线上彩色)

以裂纹扩展变化关联函数为基础，基于缺陷失效评定图计算得出缺陷安全衰减路径，提出路径速度积安全裕度动态计算模型，实际表征出缺陷裂纹变化过程中剩余安全裕度的大小.传统安全裕度研究方法模型有射线法安全裕度模型、衰减路径法安全裕度模型和模糊评定法安全裕度模型三种，这三种安全裕度模型的计算方法见文献[4, 18]，虽然以上三种传统安全评定模型都有各自优点，但都没有考虑裂纹扩展速度即考虑时变性对于安全裕度表征的影响进行准确判定.因此基于衰减路径法安全裕度模型，考虑裂纹时变性的问题，提出新的剩余安全裕度模型.

3.1 路径速度积安全裕度模型

3.1.1 衰减路径与速率拐点 由图6可知，随着裂纹尺寸变化，失效评定图上失效点从D到C的变化并非呈现射线状变化而是呈现曲线状变化，且疏密程度不同的失效点逐渐靠近缺陷失效曲线(FAC)，将DC所连成的散点曲线称为衰减路径，仿真过程中由于裂纹类型变化或者规则化处理的原因衰减路径会出现断点跳跃的情况[2]. 同时，从图7[19-20]裂纹扩展速率图中可以看出，从第二阶段到第三阶段速度突然增加时存在一个分界点C，将该点称为“速率拐点”. 对应衰减路径图6中存在某一失效点到达速率拐点临界线之后，任意两个失效点之间的距离突然逐渐增大，将该点称也定义“速率拐点”.

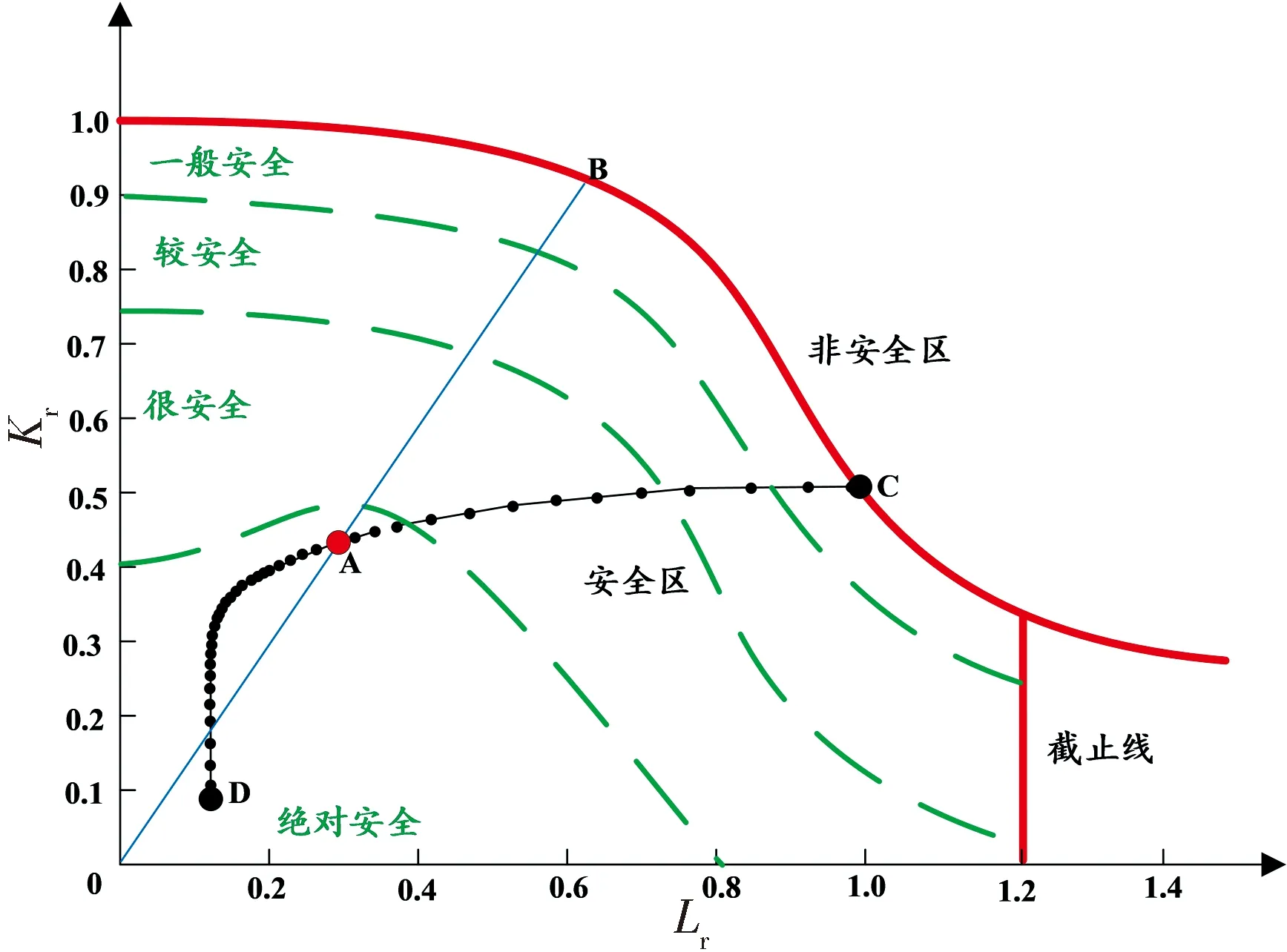
图6 三种安全裕度模型示意图

图7 长短裂纹速率变化示意图

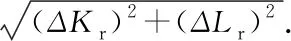
(15)

裂纹扩展中裂纹增长量为Δa，考虑厚度大小无量纲化处理后有Δa/t，则裂纹增长长度可表示为an/t=Δa1/t+Δa2/t+...+Δan/t，失效路径表征为：

(16)

将含缺陷的衰减速率图转化成图8的υ-S图，该图能反映裂纹失效速度υ随裂纹扩展变化长度的趋势，其变化趋势与图7的变化趋势极为一致.其中，S0点表示缺陷裂纹开始扩展，S1点表示第二阶段开始点，Si点表示扩展过程中任一点，Sn表示速率拐点.

3.1.3 路径速度积剩余安全裕度表征 不同大小的缺陷裂纹尺寸与失效速度有关，同时反映了设备的安全程度. 由于第三阶段失稳崩溃速度较快，考虑到压力容器评定安全性问题，这里将速率拐点作为分界线，在速度积安全裕度计算过程中把第三阶段作省略处理. 利用υ-S路径速度积对应面积来表示其剩余的安全裕度大小如图8.

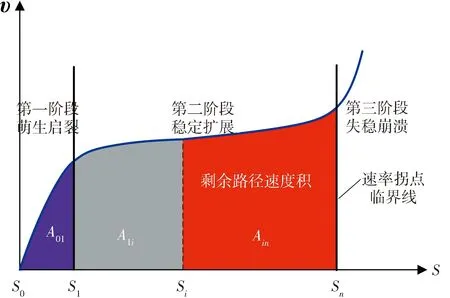
图8 表面裂纹速度积计算示意图

将扩展过程中任一点Si的速度积大小用Ai表示：

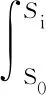
(17)

分析式(17)可知，Ai的大小是S对υ积分求面积，同理，如图8，对任意两个点Si，Sj之间的速度积大小可定义为：

(18)

根据以上定义，对于剩余速度积Ain和全域速度积A的计算可分别定义为

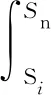
(19)

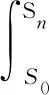
(20)

以表面裂纹情况计算，衰减路径转化后得到速度积散点曲线υ(S)，将各个点运用插值法拟合成图8的幂函数曲线，可表示为：

(21)

其中bi(i=1, 2, 3，...，M)表示常数.

通过以上定义可知，全域速度积还可代换为A=Ai+Ain，则安全系数F=A/Ai，计算失效点Si的剩余安全裕度为：

M=1-1/F=Ain/A=Ai+Ain/A

(22)

随着裂纹扩展安全裕度不断降低，红色面积Ain逐渐快速趋向于0.

3.2 速度积安全裕度模型实例

以压力容器常用材料为16MnR为例，假设壁厚t=20 mm的容器内部存在一条初始裂纹深度a0=6 mm，长度2c0=30 mm的表面裂纹，即(a/t)0=0.3, (a/c)0=0.4.通过关联函数模型计算并拟合得到y=1.12343x1+1.73772x2-5.88087x3+5.21485x4-1.62323x5+0.01806的关联函数，然后计算得到安全衰减路径. 由于裂纹扩展过程中变成穿透裂纹，所以出现断点跳跃情况. 同时考虑了形成初始裂纹之前的微小短裂纹扩展，且假设微小短裂纹的扩展情况满足上面长裂纹拟合的深度与长度变化的关联函数表达式，最终得到裂纹从裂纹源形成到失效的全域衰减路径，如图9.

图9 表面裂纹安全衰减路径实例计算示意图Fig.9 Schematic diagram of calculation of safety attenuation path of surface crack

通过关联函数计算裂纹从微小短裂纹出现到最后崩溃的全域衰减路径，同样进行速度积转化，如图，由放大图可以看出考虑微裂纹扩展时，裂纹扩展速率是先增大后减小最后进入长裂纹扩展阶段，其趋势与图7中长短裂纹变化一致，同时文献[19-20]也指出短裂纹扩展速度随长度增长而降低，到达某一尺寸后再迅速增大然后进入长裂纹扩展速率趋势.计算安全裕度时考虑其速率拐点，取速度变化量是前一次速度变化量的两倍为速率拐点作临界线，这里取速率拐点为S=0.874 5,υ=0.306 77，对应则的Lr=0.5450,Kr=0.4660，如图10.

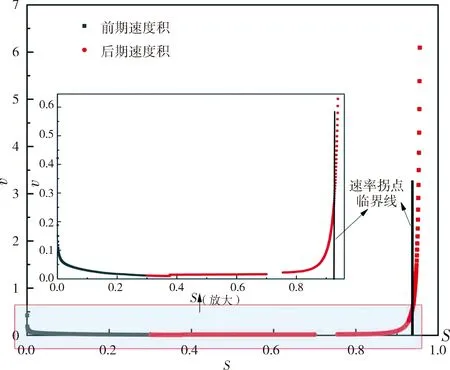
图10 表面裂纹速度积实例计算示意图Fig.10 Schematic diagram of calculation of surface crack velocity product example

将临界线后面第三阶段速度进行省略然后利用速度积分求面积来表征安全裕度，与射线法，衰减路径法和模糊评定法计算的安全裕度进行比较，运用寿命安全裕度评估剩余路径速度积安全裕度模型的合理性，计算结果由图11和表3所示.

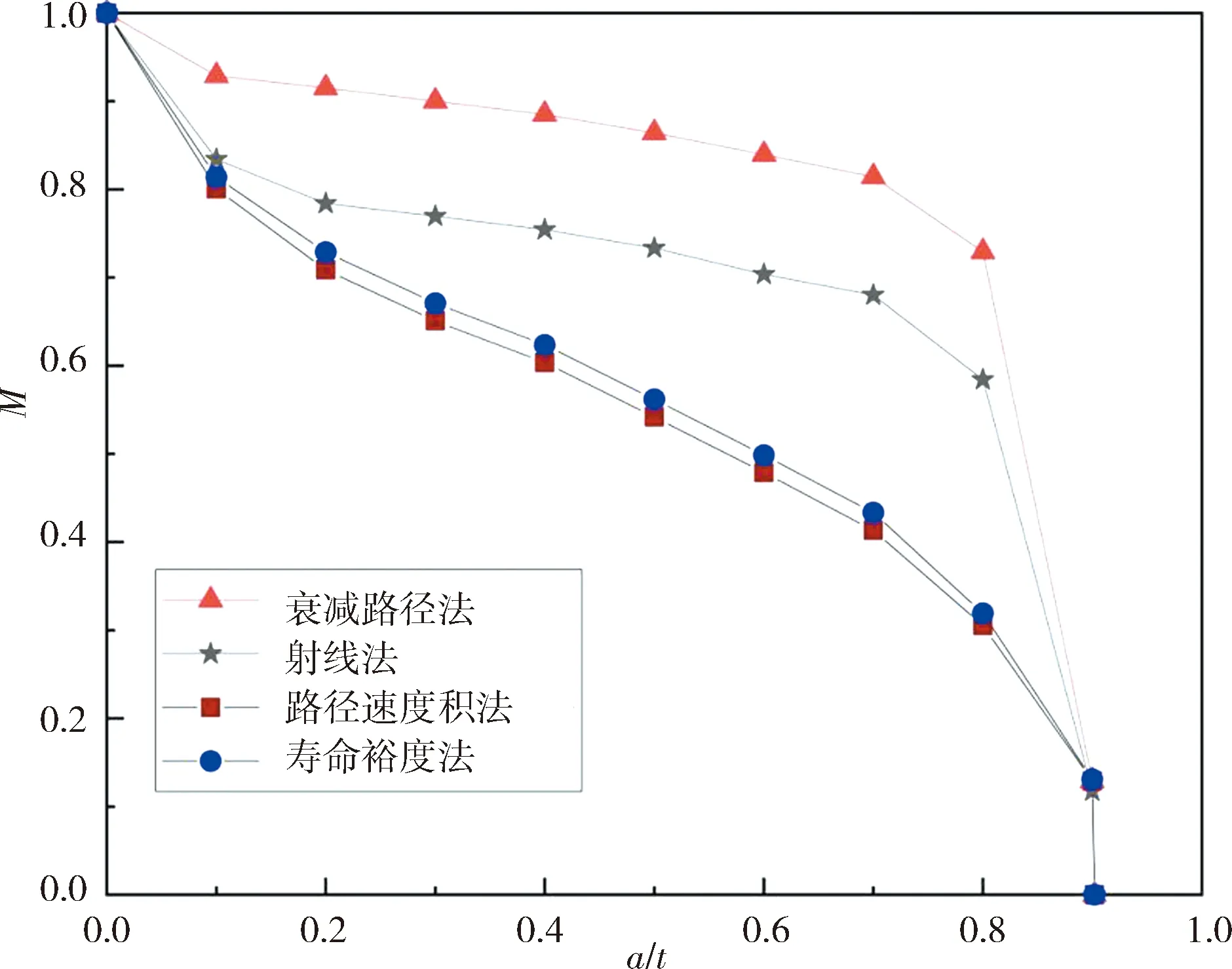
图11 安全裕度实例计算对比图

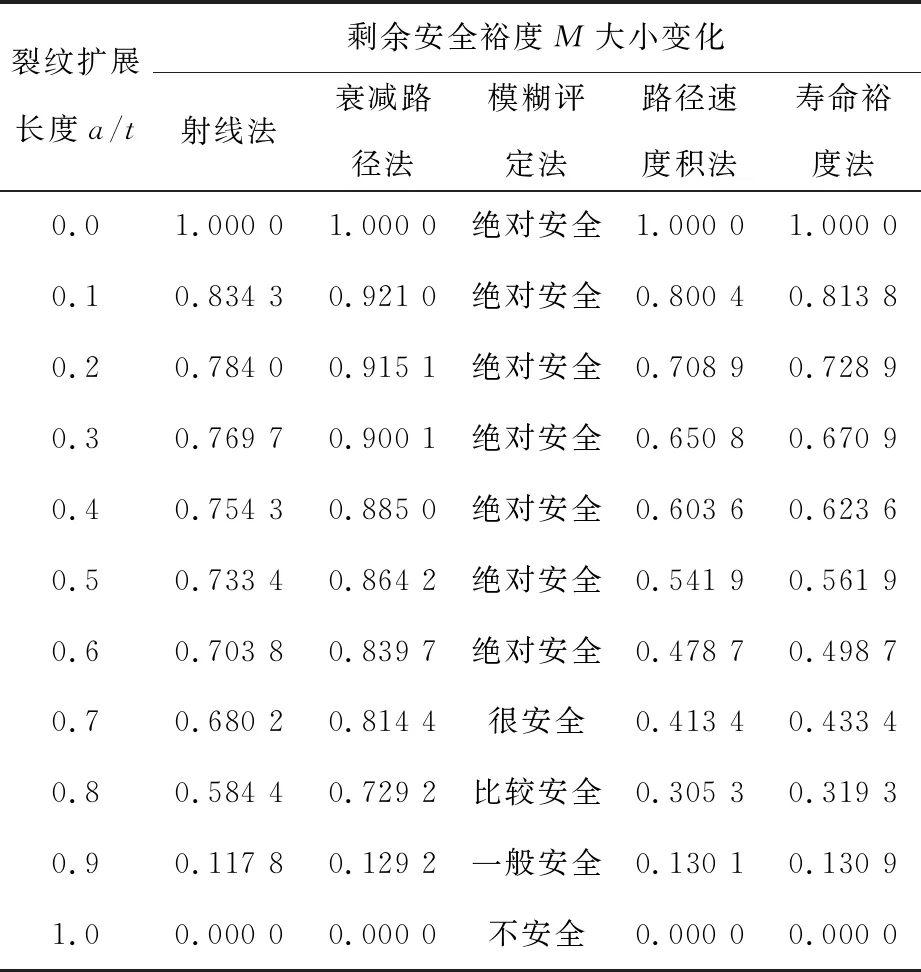
表3 裂纹变化时的剩余安全裕度大小

从图11和表3可以看出，裂纹扩展尺寸均匀变化时，射线法，衰减路径法和模糊评定法变化趋势初期比较平缓，当到达0.8后时，剩余裕度会出现突然降低的变化，而路径速度积随着裂纹尺寸变化趋势平缓且与图8中速度υ有关，速度越大安全裕度下降越快.计算的寿命裕度变化与路径速度积变化规律基本也一致.与衰减路径法相比，路径速度积法的差别可达42%左右，而与寿命裕度法相比最大差别仅为2%.说明路径速度积法更符合裂纹扩展下安全裕度变化，能较好的实时表征动态安全裕度的大小.

4 结 论

本文主要针对含缺陷压力容器安全评估展开研究.传统安全裕度判定方法如射线法只能判断设备是否安全，而无法准确得出剩余安全裕度大小，针对这一局限，本文通过找出不同类型裂纹扩展形状关联变化函数，得到裂纹的安全衰减路径，进而考虑裂纹扩展变化中的时变性建立路径速度积的安全裕度表征模型.并与射线法、衰减路径法和模糊评定法进行比较，从剩余寿命法角度对比了其实用性，论证模型的可靠性.本文主要研究内容如下：(1) 基于Paris公式进行迭代得到裂纹扩展规律公式，应用Newman等的数值计算K的理论，考虑裂纹存在闭合效应下埋藏裂纹和表面裂纹扩展规律变化情况，改变Paris公式中材料系数m证明裂纹扩展变化与材料有关，并利用Python计算机语言进行模型编程，得到不同初始值下裂纹的变化规律图，建立埋藏裂纹和表面裂纹在扩展过程中深度a和长度c的关联变化函数.(2) 基于传统安全裕度模型无法考虑裂纹扩展下时变性问题，根据速度积概念，建立了新的大型压力容器剩余安全裕度模型.以表面裂纹为例进行讨论分析，从寿命安全裕度角度评价路径速度积安全裕度模型，结果符合较好.