基于扰动观测器的时变负载四旋翼无人机自适应有限时间控制
武晓晶 郑文棪 吴学礼 甄然 邵士凯


摘 要:针对具有未知外部扰动和阻力系数的时变负载四旋翼无人机系统,提出了一种复合有限时间控制策略。首先,通過牛顿-欧拉方法建立了完整的四旋翼无人机数学模型。位置环采用自适应参数校正方法对负载进行估计,并与反步递推控制相结合,在阻力系数未知情况下设计了自适应轨迹跟踪控制器。其次,采用基于扰动观测器的有限时间滑模控制器,并利用Lyapunov稳定性理论进行无人机系统位置环和姿态环渐近稳定和有限时间稳定性验证。最后,通过数值仿真进行验证。结果表明,所提控制器提高了系统的收敛速度,减少了外界扰动对系统的影响。研究方法克服了已有研究要求阻力系数和负载已知的局限性,提高了系统的抗干扰能力,对于增强四旋翼无人机的实际应用性具有一定的参考价值。
关键词:自动控制理论;四旋翼无人机;时变负载;扰动观测器;反步递推控制;滑模控制
中图分类号:TN958.98 文献标识码:A
doi:10.7535/hbkd.2021yx06005
Adaptive finite-time control for quadrotor UAV with time-varying load based on disturbance observer
WU Xiaojing1,ZHENG Wenyan1,WU Xueli1,2,ZHEN Ran1,SHAO Shikai1
(1.School of Electrical Engineering,Hebei University of Science and Technology,shijiazhuang,Hebei 050018,China;2.Hebei Provincial Research Center for Technologies in Process Engineering Automation,Shijiazhuang,Hebei 050018,China)
Abstract:For the quadrotor unmanned aerial vehicle (UAV) system with time-varying load,the compound finite-time control strategy was proposed in the presence of unknown external disturbances and unknown drag coefficients.Firstly,a complete mathematical model of quadrotor UAV was established by Newton-Euler method .An adaptive trajectory tracking controller with unknown drag coefficient was designed by combining the adaptive parameter correction method of position loop with backstepping control to estimate load.Then,a finite-time sliding mode controller and Lyapunov stability theory were used so that the position loop and the attitude loop were proved to be asymptotically stable and finite-time stable,respectively.Finally,it was verified by numerical simulation.The results show that the proposed controller improves the system convergence rate,and reduces the influence of outside disturbance to the system.This method overcomes the limitations of known drag coefficients and load in the existing research,improves the anti-interference ability of the system,and has certain reference value for enhancing the practical application of the quadrotor UAV.
Keywords:
automatic control theory;quadrotor unmanned aerial vehicle (UAV);time-varying load;disturbance observer;backstepping control;sliding mode control
四旋翼无人机具有体积小、携带方便、使用简单、价格便宜、机动性较强等特点。近年来,其应用范围逐渐从军事领域扩展到民用领域[1]。在工业生产线巡检、农作物生长情况监测、实时画面转播、道路监管等领域被广泛使用[2],因此,无人机的控制问题受到了广泛关注。众所周知,四旋翼无人机是一种典型的非线性、欠驱动、强耦合系统,又由于其质量较小、易受风扰动,给无人机在实际应用中的控制问题带来了巨大挑战[3]。
针对四旋翼无人机的控制问题,传统的PID控制算法[4-5]、LQR控制算法[6-8]等线性控制方法先后被应用于无人机控制上,但是这些线性控制方法不能保证无人机系统具有较好的控制性能。随后,反步控制、自适应控制、滑模控制等一系列非线性控制方法被相继提出[9-13]。文献[9]针对存在参数不确定性和外部扰动的四旋翼无人机系统,设计了基于扰动观测器的自适应滑模控制策略。文献[10]结合鲁棒自适应反推控制方法和快速终端滑模控制方法,确保系统的稳定性和控制器的鲁棒性。文献[11]研究了一类具有未知外部复合扰动的四旋翼无人机姿态系统,提出一种新的指数式非奇异终端滑模控制,使系统获得了较好的控制性能。为了实现存在参数不确定性的四旋翼无人机系统姿态轨迹的全局渐近跟踪,文献[12]提出了一种自适应滑模反推控制方案。文献[13]针对存在外部风扰的无人机系统,设计了基于非线性扩张观测器的滑模控制器,并通过仿真实验,验证了跟踪误差的收敛性。然而,上述研究都是针对具有固定负载的无人机进行研究,而在实际应用中,四旋翼无人机经常被用于运输货物和喷洒农药等工作,负载可能是时变的。
为了解决上述问题,文献[14—16]研究了具有时变负载的四旋翼无人机的控制方法。其中,文獻[14]为四旋翼无人机系统设计了一种自适应控制器,用来补偿负载质量的不确定性。文献[15]提出了一种基于反推法的分数滑模控制器用于具有时变负载的四旋翼无人机系统,该控制器实现了控制系统跟踪轨迹的渐近稳定。文献[16]基于滑模控制方法设计了一种鲁棒控制方案,实现了存在时变负载的四旋翼无人机姿态跟踪误差的渐近稳定。
然而,上述研究所提出的控制方法都只能保证四旋翼无人机系统渐近稳定,即:系统状态只有当时间趋近于无穷大的时候才能收敛到平衡点。实际应用中,对四旋翼无人机系统收敛的快速性提出了更高的要求,有限时间控制可以确保状态变量在限定的时间内收敛到平衡点。因此,四旋翼无人机系统的有限时间控制研究具有非常重要的意义。文献[17]针对四旋翼无人机姿态子系统,基于指定姿态轨迹,提出了一种基于有限时间控制的姿态跟踪算法,但是,此系统阻力系数已知,而且没有考虑位置子系统的控制器设计。文献[18]针对具有未知外部扰动的四旋翼无人机系统,基于改进的Overtorque等效控制算法,提出了一种自适应多变量有限时间稳定控制算法,但是没有考虑无人机的时变负载。文献[19—20]基于扰动观测器,针对四旋翼无人机设计了有限时间控制器,然而,此研究未考虑阻力系数未知和时变负载对系统的影响。
基于以上分析,本文面向具有未知外部扰动、时变负载和未知阻力系数的四旋翼无人机系统,分别针对位置环和姿态环,提出了自适应反步递推控制方法和基于扰动观测器的有限时间滑模控制方法。
1 四旋翼无人机数学模型
四旋翼无人机“Ⅹ”形机身结构如图1所示。
无人机的4个旋翼分别由4个电机驱动,2个相邻旋翼的旋转方向相反。Ωii=1,2,3,4为转子的角速度。惯性参考坐标系E=ex,ey,ez描述无人机相对于地面的位置变化。机身固定坐标系B=bx,by,bz描述四旋翼的空间位置坐标。三维空间中,状态变量ξ=x,y,zT和δ=,θ,ψT分别描述无人机系统的位置信息和姿态信息。其中姿态角,θ,ψ分别代表滚转角、俯仰角、偏航角。根据设计要求,给出姿态角的范围(-π/2<<π/2)、(-π/2<θ<π/2)、(-π/2<ψ<π/2)。为了建立准确并适合于控制器设计的数学模型,对四旋翼无人机系统进行以下假设:
假设1四旋翼无人机是一类刚体;
假设2四旋翼无人机的机体结构是对称的;
假设3四旋翼无人机飞行过程中,重力加速度不随位置的变化而变化;
假设4惯性参考系是地面,机身重心与刚体固定坐标系的原点重合。
3 数值仿真
为了验证定理1和定理3中所提出的四旋翼无人机自适应反步控制器和有限时间滑模控制器的有效性和优越性,采用Matlab软件进行仿真,并在设计参数相同的条件下与不考虑时变负载的控制器进行对比。四旋翼无人机系统的初始状态值设置为(x,y,z)=(0.1,2.5,2) m和(,θ,ψ)=(0.4π,0.4π,0.4π) rad,选取参考轨迹xd=2cos t,
yd=2sin t,zd=0.5t,ψd=0,
外部扰动
机模型参数和控制器设计参数分别如表1和表2所示。
为了探究时变负载对控制器的影响,将四旋翼的质量和负载变化模拟为正弦函数,静态过载和指数下降的连续状态,飞行过程中的负载变化曲线如图3所示。相应的仿真结果如图4—图8所示。
该系统的三维轨迹图和各个方向的投影图如图4所示。图5和图6分别表示位置子系统和姿态子系统的跟踪曲线。位置子系统x,y,z的跟踪误差曲线ex=x-xd,ey=y-yd,ez=z-zd和姿态子系统,θ,ψ的跟踪误差曲线e=-d,eθ=θ-θd,eψ=ψ-ψd如图7和图8所示。由图4—图8可知,所设计的控制器使得四旋翼无人机系统具有较好的跟踪性能。
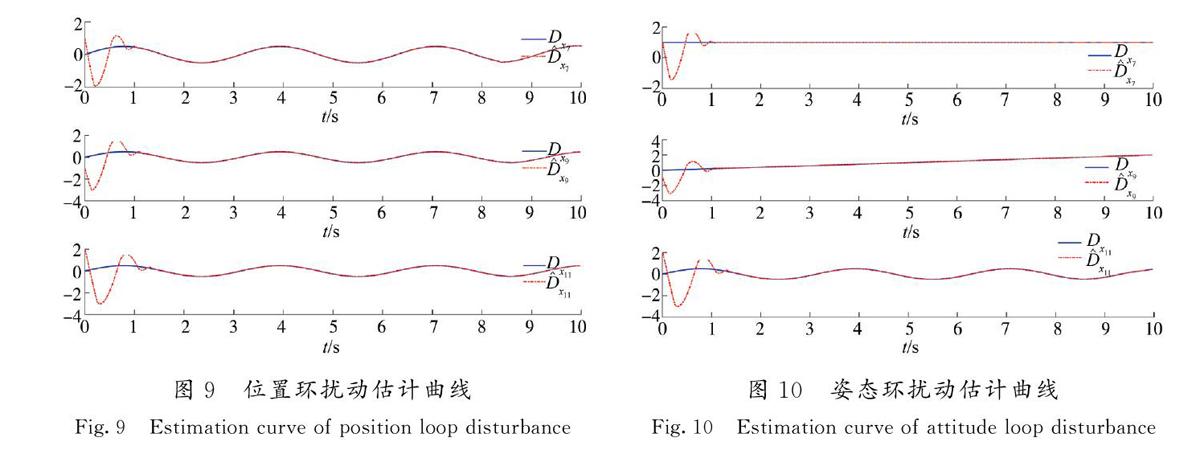
扰动观测器对外部扰动的估计曲线如图9所示,观测器可以准确地估计外部扰动。此外,为了验证扰动观测器对不同扰动的有效性,图10显示了扰动观测器针对不同外部扰动Dx7=1,Dx9=0.2t,Dx11=0.5sin2t的估计曲线。由图9和图10可知,扰动观测器可以在有限时间内准确地估计未知的外部扰动。
为了说明本文控制方法的优越性,与文献[19]的控制方法进行对比仿真。得到的对比仿真结果如图11—图12所示。其中,位置子系统轨迹跟踪曲线如图11所示,姿态子系统轨迹跟踪曲线如图12所示。由图11可知,本文提出的控制策略具有更好的跟踪性能。由图12可知,本文所提出的有限时间控制方法可以提高姿态子系统的跟踪速度。
4 结 语
本文针对具有未知阻力系数、未知外部扰动和时变负载的四旋翼无人机系统设计了位置环和姿态环控制器。考虑了实际飞行过程中,四旋翼无人机系统同时具有时变负载、未知外部扰动和未知阻力系数的情况,利用自适应控制策略,打破了已有研究的局限性,提高了系统的收敛速度和鲁棒性;同时,针对四旋翼无人机系统姿态环,提出了一种新的滑模面。基于所设计的滑模面和扰动观测器,设计了有限时间控制策略,提高了系统的收敛速度,减少了外界扰动对系统的影响。
本文所设计的控制器虽然使得系统能够在有限时间内收敛,但尚未实现系统状态未知时的有限时间控制。接下来需要进一步完善数学模型和控制器,使四旋翼无人机系统能够实现输出反馈控制,更符合实际需求,进而达到更好的控制效果。
参考文献/References:
[1] 方璇,钟伯成.四旋翼飞行器的研究与应用[J].上海工程技术大学学报,2015,29(2):113-118.
FANG Xuan,ZHONG Bocheng.Research and application of four-rotor aircraft[J].Journal of Shanghai University of Engineering Science,2015,29(2):113-118.
[2] PHILLIPS B,HRISHIKESHAVAN V,YEO D,et al.Flight performance of a package delivery quadrotor biplane[C]//7th American Helicopter Society Technical Meeting on VTOL Unmanned Aircraft Systems and Autonomy.[S.l.]:American Helicopter Society International,2017:1-11.
[3] BERGAMASCO M,LOVERA M.Identification of linear models for the dynamics of a hovering quadrotor[J].IEEE Transactions on Control Systems Technology,2014,22(5):1696-1707.
[4] GARCA R A,RUBIO F R,ORTEGA M G.Robust PID control of the quadrotor helicopter[J].IFAC Proceedings Volumes,2012,45(3):229-234.
[5] ZHONGHAO D Y.PID control of four-rotor aircraft based on quaternion[J].Applied Mechanics and Materials,2014,484/485:1071-1075.
[6] ALOTHMAN Y,GUO M H,GU D B.Using iterative LQR to control two quadrotors transporting a cable-suspended load[J].IFAC-Papers-OnLine,2017,50(1):4324-4329.
[7] 王志方,付興建,李同.四旋翼飞行器的LQR优化控制[J].传感器世界,2017,23(3):17-23.
WANG Zhifang,FU Xingjian,LI Tong.LQR optimal control for quadrotor aircraft[J].Sensor World,2017,23(3):17-23.
[8] RYAN T,JIN KIM H.LMI-based gain synthesis for simple robust quadrotor control[J].IEEE Transactions on Automation Science and Engineering,2013,10(4):1173-1178.
[9] WANG B,YU X,MU L X,et al.Disturbance observer-based adaptive fault-tolerant control for a quadrotor helicopter subject to parametric uncertainties and external disturbances[J].Mechanical Systems and Signal Processing,2019,120:727-743.
[10]LABBADI M,CHERKAOUI M.Robust adaptive backstepping fast terminal sliding mode controller for uncertain quadrotor UAV[J].Aerospace Science andTechnology,2019,93.doi:10.1016/j.ast.2019.105306.
[11]LIU H B,WANG H P,SUN J L.Attitude control for QTR using exponential nonsingular terminal sliding mode control[J].Journal of Systems Engineering and Electronics,2019,30(1):191-200.
[12]CHINGOZHA T,NYANDORO O.Adaptive sliding backstepping control of quadrotor UAV attitude[J].IFAC Proceedings Volumes,2014,47(3):11043-11048.
[13]ZHAO L,DAI L W,XIA Y Q,et al.Attitude control for quadrotors subjected to wind disturbances via active disturbance rejection control and integral sliding mode control[J].Mechanical Systems and Signal Processing,2019,129:531-545.
[14]DAI S C,LEE T,BERNSTEIN D S.Adaptive control of a quadrotor UAV transporting a cable-suspended load with unknown mass[C]//53rd IEEE Conference on Decision and Control.[S.l.]:IEEE,2014:6149-6154.
[15]VAHDANIPOUR M,KHODABANDEH M.Adaptive fractional order sliding mode control for a quadrotor with a varying load[J].Aerospace Science and Technology,2019,86:737-747.
[16]WU X W,XIAO B,QU Y H.Modeling and sliding mode-based attitude tracking control of a quadrotor UAV with time-varying mass[J/OL].ISA Transactions.[2019-08-17].https://pubmed.ncbi.nlm.nih.gov/31439392/.
[17]ZHANG J,DU H B,ZHU W W,et al.Attitude trajectory planning and finite-time attitude tracking control for a quadrotor aircraft[C]//IECON 2018-44th Annual Conference of the IEEE Industrial Electronics Society.[S.l.]:IEEE,2018:6167-6171.
[18]TIAN B L,CUI J,LU H C,et al.Adaptive finite-time attitude tracking of quadrotors with experiments and comparisons[J].IEEE Transactions on Industrial Electronics,2019,66(12):9428-9438.
[19]WANG N,DENG Q,XIE G M,et al.Hybrid finite-time trajectory tracking control of a quadrotor[J].ISA Transactions,2019,90:278-286.
[20]SHARMA M,KAR I.Finite time disturbance observer based geometric control of quadrotors[J].IFAC-PapersOnLine,2020,53(1):295-300.
[21]SHEN Y J,HUANG Y H.Uniformly observable and globally Lipschitzian nonlinear systems admit global finite-time observers[J].IEEE Transactions on Automatic Control,2009,54(11):2621-2625.
[22]SHTESSEL Y B,SHKOLNIKOV I A,LEVANT A.Smooth second-order sliding modes:Missile guidance application[J].Automatica,2007,43(8):1470-1476.
[23]ZHANG J Q,GU D W,REN Z H,et al.Robust trajectory tracking controller for quadrotor helicopter based on a novel composite control scheme[J].Aerospace Science and Technology,2019,85:199-215.
收稿日期:2021-04-21;修回日期:2021-09-10;責任编辑:冯 民
基金项目:国家自然科学基金(62003129,61903122);河北省研究生创新资助项目(CXZZSS2021098);国防基础计划研究项目;河北省重点研发计划项目(19250801D)
第一作者简介:武晓晶(1985—),女,河北石家庄人,副教授,博士,主要从事非线性系统控制及无人机自主飞行控制、协同控制方面的研究。
通讯作者:甄 然教授。E-mail:zhenranzr@126.com
武晓晶,郑文棪,吴学礼,等.
基于扰动观测器的时变负载四旋翼无人机自适应有限时间控制
[J].河北科技大学学报,2021,42(6):579-590.
WU Xiaojing,ZHENG Wenyan,WU Xueli,et al.
Adaptive finite-time control for quadrotor UAV with time-varying load based on disturbance observer
[J].Journal of Hebei University of Science and Technology,2021,42(6):579-590.

