传感器电解质材料热膨胀性能和热稳定性变化规律研究

高君华， 郑瑞伦

(1.重庆文理学院 电子信息与电气工程学院， 重庆 402160； 2. 黑龙江大学 电子工程学院， 哈尔滨 150080)

1 引 言

固体电解质氧传感器在国防军事、空间技术和汽车工业中具有非常重要的应用价值，其中氧化锆(ZrO2)固体电解质传感器可以监测和控制各种燃料气氛冶金反应等，已广泛应用于环保、材料、化工、冶金、能源、宇航等领域，是应用最为广泛的固体电解质氧传感器.氧传感器主要由铂电极和钇稳定的氧化锆固体电解质材料制成[1].由于长期工作于高温可变的环境，氧传感器的热力学性能随温度变化显著，这不仅直接影响传感器的工作温度和性能，而且电解质与电极材料等材料因热膨胀系数变化不同引起开裂、形变、脱落等，将直接影响传感器的工作寿命.因此，探讨钇稳定氧化锆固体电解质的热力学性能及热稳定性随温度和时间的变化规律，是一个亟待解决的重要问题.为此，明确氧化锆(ZrO2)的热膨胀等热力学性能及其热稳定性具有重要有意义.目前，国内外已有一些文献对ZrO2固体电解质的热学性能进行了研究.

Yang等[2]研究了尺寸效应对传统烧结法制备ZrO2/ ZrW2O8复合材料热膨胀的影响；戴建伟等[3]研究了ZrO2掺杂对La2Ce2O7力学性能以及热膨胀系数、热传导率等热物理性能的影响；Maneesha等[4]采用脉冲激光沉积技术沉积了ZrO2/ Y2O3多层膜，并对其热稳定性和热膨胀性质进行了研究；Kostanovskiy等[5]在1200 K～2700 K温度范围内，对ZrO2的线性膨胀和热系数进行了实验研究；Wang等[6]研究了非晶硅和硅酸盐稳定的ZrO2中空纤维的热导率和热稳定性；Ansari等[7]采用准谐波近似(QHA)的密度泛函理论(DFT)计算了温度变化对单层ZrO2纳米片弹性性能的影响；Gorelov[8]研究了ZrO2中的高温相变问题；Jin等[9]在广义梯度近似(GGA)和准谐波德拜模型中，利用平面波伪势法研究了四方ZrO2在高压和高温下的热力学性质；Kwon等[10]纳米粉体在1200 ℃烧结制备了高密度单斜晶系ZrO2，研究了老化和再热单斜ZrO2电导率的变化.但这些文献主要是对ZrO2的热力学性质进行的实验研究，而未从理论角度深入探讨影响单斜相ZrO2的热膨胀系数及其热稳定性的内在因素.

因此，本文将应用固体物理理论，研究氧传感器固体电解质ZrO2的热膨胀等热力学性能及其热稳定性随温度和时间的变化规律，探讨原子非简谐振动的影响，以期对解决固体电解质氧传感器稳定性问题提供理论指导意义.

2 物理模型和简谐系数与非简谐系数

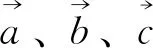
图1 ZrO2的单斜相结构与原子分布Fig. 1 Monoclinic structure and atom distribution of ZrO2

ZrO2固体电解质通常工作于较高温环境，研究它热力学性质时，可不考虑原子内部电子的运动，将原子视为彼此相互作用的质点，每个原子在平衡位置附近作非简谐振动.设最近原子距离为r，一个原子平均相互作用能为φ(r)，将φ(r)在平衡位置r0附近展开，偏离ξ=r-r0很小时，有：

(1)

其中，ε0、ε1、ε0分别是简谐系数和第一、第二非简谐系数.

对Zr这类过渡金属，Zr-Zr原子相互作用势可写为[11]：

(2)

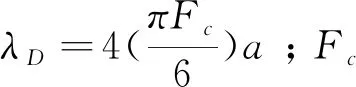
对Zr-O这类离子键结合，Zr-O原子相互作用势可写为[12]：

(3)

这里，q=2e是锆(Zr)离子的电荷；α为马德隆常数：α=1.6381；z0为锆(Zr)离子最近邻的离子数；ρ为排斥相互作用范围参数，可取为锆(Zr)离子半径的5倍；λ为排斥能参量，取λz0=2.1×10-8erg[12].

对氧原子与氧原子，两原子相互作用势可写为范德瓦尔势形式[13]：

(4)

其中，D为阱深；r0为φ(r)=0时两原子间距离，a、b、r0、D可由具体势能曲线来确定.

由(2)、(3)和(4)式，结合图1所示结构，可求得考虑到最近邻(第1近邻)、次近邻(第2近邻)、再次近邻(第3近邻)……，一个锆(Zr)原子受到的平均相互作用能φZr(r)和一个氧(O)原子受到的平均相互作用能φO(r)，进而求得氧(O)原子和锆(Zr)原子振动的简谐系数ε0O、ε0Zr和第一非简谐系数ε1O、ε1Zr以及第二非简谐系数ε2O、ε2Zr

3 原子振动频率和阻尼系数随温度和时间的变化

3.1 原子的振动频率随温度的变化

在原子相互作用下，ZrO2中的每个原子都在其平衡位置附近振动.尽管各原子振动方向不同，但原子的振动频率与振动方向无关.按照固体物理理论[14]，考虑到原子非简谐振动后，原子的振动频率与温度有关，由此得到氧(O)原子和锆(Zr)原子的振动频率ωO和ωZr分别为：

(5)

(6)

这里，ω0O=(ε0O/MO)1/2和ω0Zr=(ε0Zr/MZr)1/2分别为T=0 K时氧原子和锆原子的振动频率.

ZrO2的质心的平均振动频率为：

(7)

3.2 原子的阻尼系数随温度的变化

简谐近似下，原子的运动为等振幅A0和频率为常数的简谐运动.实际原子做的是非简谐运动，不仅原子振动频率不为常数，而且振动会产生大量的声子，声子之间以及声子与材料存在的缺陷(界面、杂质、空位等)之间有相互作用，则必定存在能量损失，使得材料性能降低而缩短使用寿命，而原子的运动因能量损失由简谐振动变为阻尼运动.文献[15]已求出原子的阻尼系数β随温度的变化关系，由此可得：氧(O)原子和锆原子的阻尼系数βO、βzr随温度的变化分别为：

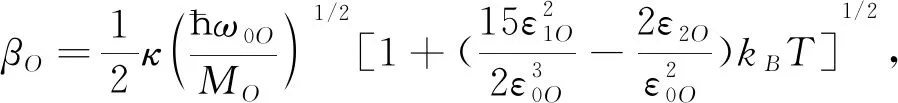
(8)

式中的κ为阻尼对原子振动频率的影响参量.在小阻尼情况下，κ很小.具体数值可由它得到结果与实验比较确定，也可以通过具体材料的物理量随时间的衰减情况估计.

由质心运动定理可得ZrO2平均阻尼系数为：

(9)

4 材料的热膨胀系数和热稳定性随温度和时间的变化

4.1 原子的平均位移随温度和时间的变化

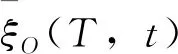
(10)

(11)

将氧化锆原子分子体系简化为位于质心的一些质点体系.取OX轴方向为原子位移方向，氧(O)原子和锆(Zr)原子的振动方向与OX轴方向夹角近似取为零.由此近似求得ZrO2质心平均位移为：

(12)

4.2 热膨胀系数随温度和时间的变化

将(9)式代入热膨胀系数αl的定义式：αl=(1/r0)∂(r0+ξ)/∂T，求得氧化锆的αl随温度和时间的变化为：

(13)

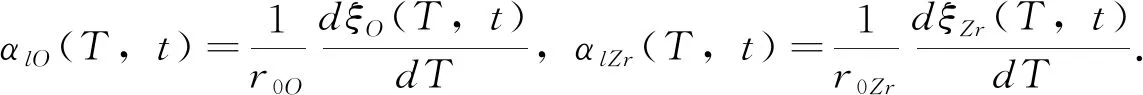
4.3 热稳定性随温度和时间的变化

材料的老化是一种普遍现象，老化会导致材料的性能逐渐降低，甚至完全丧失使用价值[16].老化的原因，除材料氧化外，温度无疑是另一个重要因素.温度的变化引起原子非简谐振动的变化，导致热膨胀性能以及其它性质发生改变.由于ZrO2固态电解质长期在高温可变的环境下工作，热膨胀、蓄热和传热等热力学性能随温度变化显著，不仅直接影响传感器的工作性能，而且电解质与电极材料等材料因热膨胀系数变化不同会引起开裂、形变、脱落等现象，将缩短传感器的工作寿命,可用温度稳定性系数(Temperathure stability)来反映热膨胀性能的热稳定性，因此，热膨胀性能温度稳定性系数[10]可定义为：

(14)

其中，αl0是开始测量时的热膨胀系数由(14)式看出，ZrO2电解质热膨胀性能稳定性，除与材料组成结构、原子相互作用势和振动情况外，还与使用时间和使用环境的温度等有关.

氧(O)原子和锆(Zr)原子阻尼系数随温度的变化率分别为：

(15)

5 原子非简谐振动对传感器电解质材料热膨胀性能和热稳定性的影响

表1给出了锆原子质量MZr、氧原子质量MO、ZrO2分子质量MZrO2、氧原子及锆原子的简谐系数ε0、第一、二非简谐系数ε1、ε2[17].

表1 原子及分子的质量、简谐及非简谐系数

由(5)-(7)式得到原子振动频率随温度的变化,见图2(a).图2(b)给出非简谐与简谐的差值，即非简谐效应对原子振动频率的影响随温度的变化图中曲线0、1、2分别是简谐、考虑到第一非简谐、同时考虑到第一、二非简谐的结果.

由图2看出：(1)简谐近似下，原子振动频率为常量；考虑到非简谐效应后，原子振动频率随温度的升高而线性增大，同时考虑第一、二非简谐的值大于只考虑第一非简谐的值；(2)温度越高，非简谐效应对原子振动频率的影响越大，即温度越高，非简谐效应越显著例如：T=300 K时，非简谐下的原子振动频率与简谐近似下的差值为3.82×1010s-1，T=1000 K时，其差值为12.74×1010s-1.

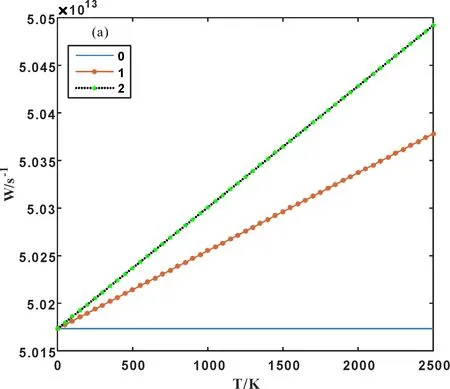
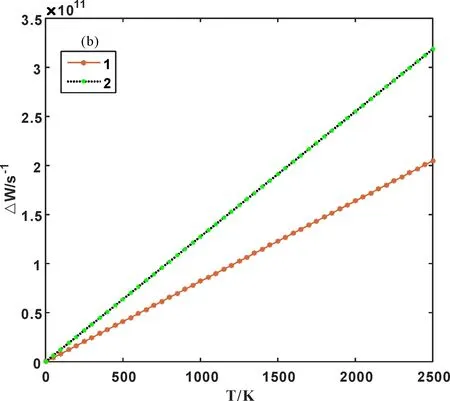
图2 原子振动频率(a)及非简谐效应的影响(b)随温度的变化Fig. 2 Changes of atomic vibration frequency: (a) and the influence of anharmonic effect on it (b) with temperature

由(8)、(9)式得到原子振动阻尼系数随温度的变化，见图3(a).图3(b)给出非简谐与简谐的差值，即非简谐效应对原子振动阻尼系数的影响随温度的变化图中曲线0、1、2的含义同图2.由图3看出：(1)简谐近似下，原子振动阻尼系数为常量；考虑到非简谐效应后，原子振动阻尼系数随温度的升高而线性增大，同时考虑第一、二非简谐的值大于只考虑第一非简谐的值；(2)考虑到非简谐效应后，温度越高，原子振动阻尼系数与简谐近似下的差值越大，即温度越高，非简谐效应越显著.例如：T=300 K时，非简谐下的原子振动频率与简谐近似下的差值为5.19×10-11s-1；T=1000 K时，其差值为17.3×10-11s-1.

由(11)、(12)式得到原子平均位移随随温度和时间的变化见图4.图中曲线0、1、2的含义同图2.

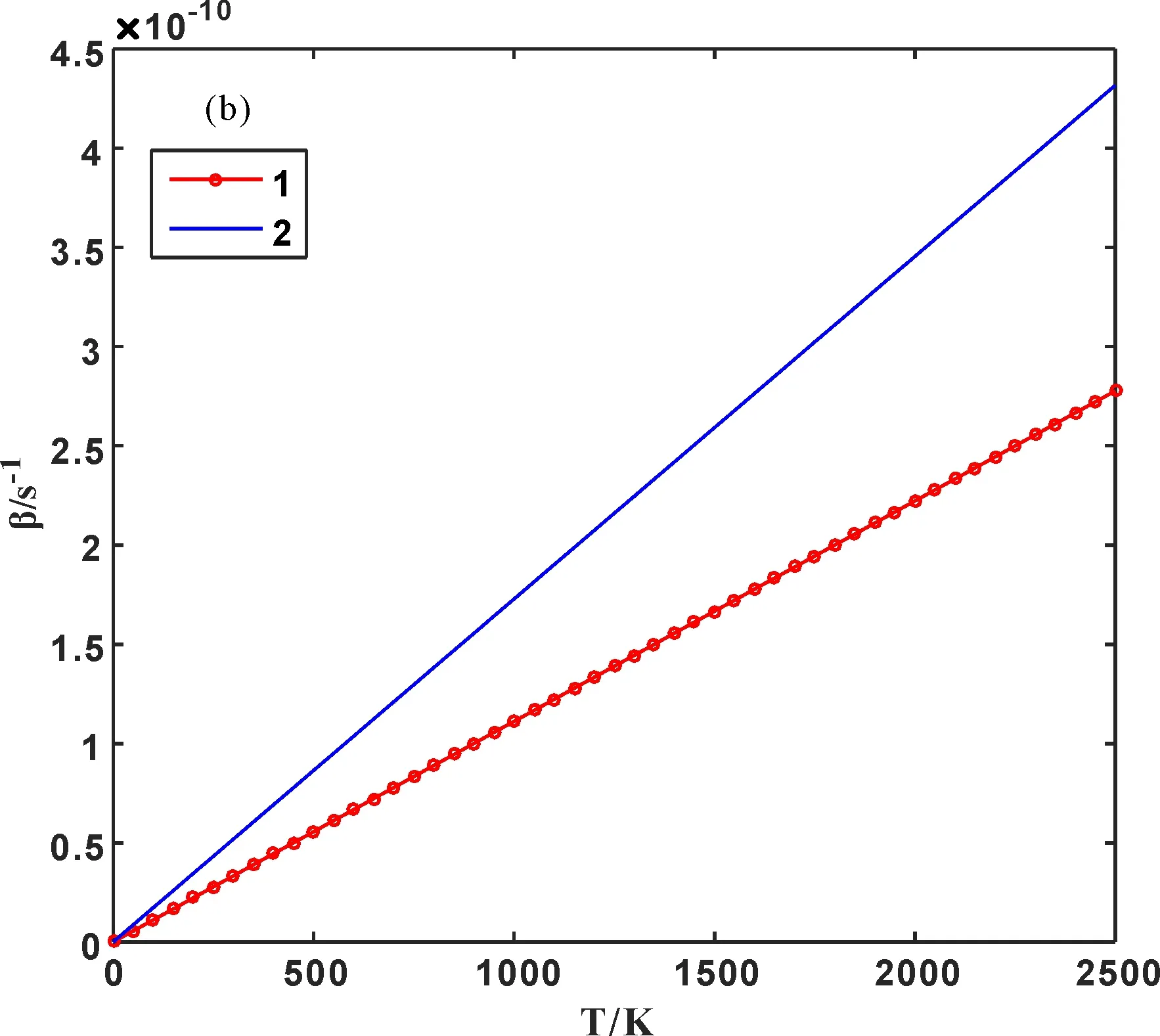
图3 原子振动阻尼系数(a)非简谐效应的影响(b)随温度的变化Fig. 3 Changes of atomic vibration damping coefficient (a) and the influence of anharmonic effect on it (b) with temperature

由图4看出,(1)简谐近似下，原子平均位移不随温度和时间而变化；(2)考虑到非简谐效应后，原子平均位移随温度的升高而线性增大，且同时考虑第一、二非简谐的值小于只考虑第一非简谐的值，但差值较小，如当温度T=300 K时，只考虑第一非简谐的原子平均位移为8.888×10-14m，而同时考虑第一、二非简谐时的值为8.887×10-14m，相差了0.11%；(3)考虑到非简谐效应后，原子平均位移随时间非线性减小，且时间越长与简谐近似结果越相近.例如：当温度T=300 K，t =100天时，非简谐下的原子平均位移为3.16×10-14m；t =300天时，其值为0.74×10-14m；而当T=800 K，t =100天时，非简谐下的原子平均位移为8.42×10-14m；t =300天时，其值为1.96×10-14m.

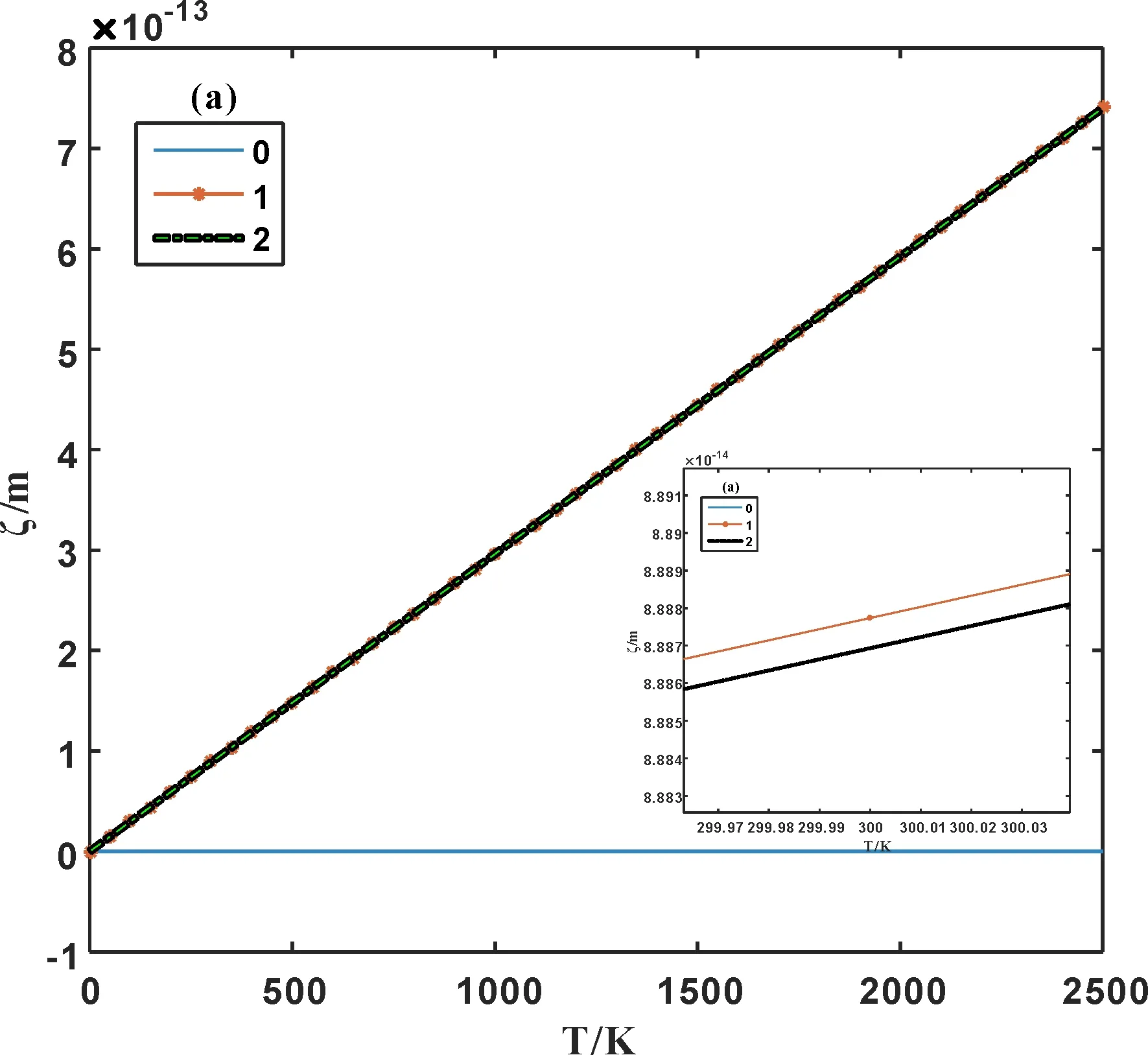
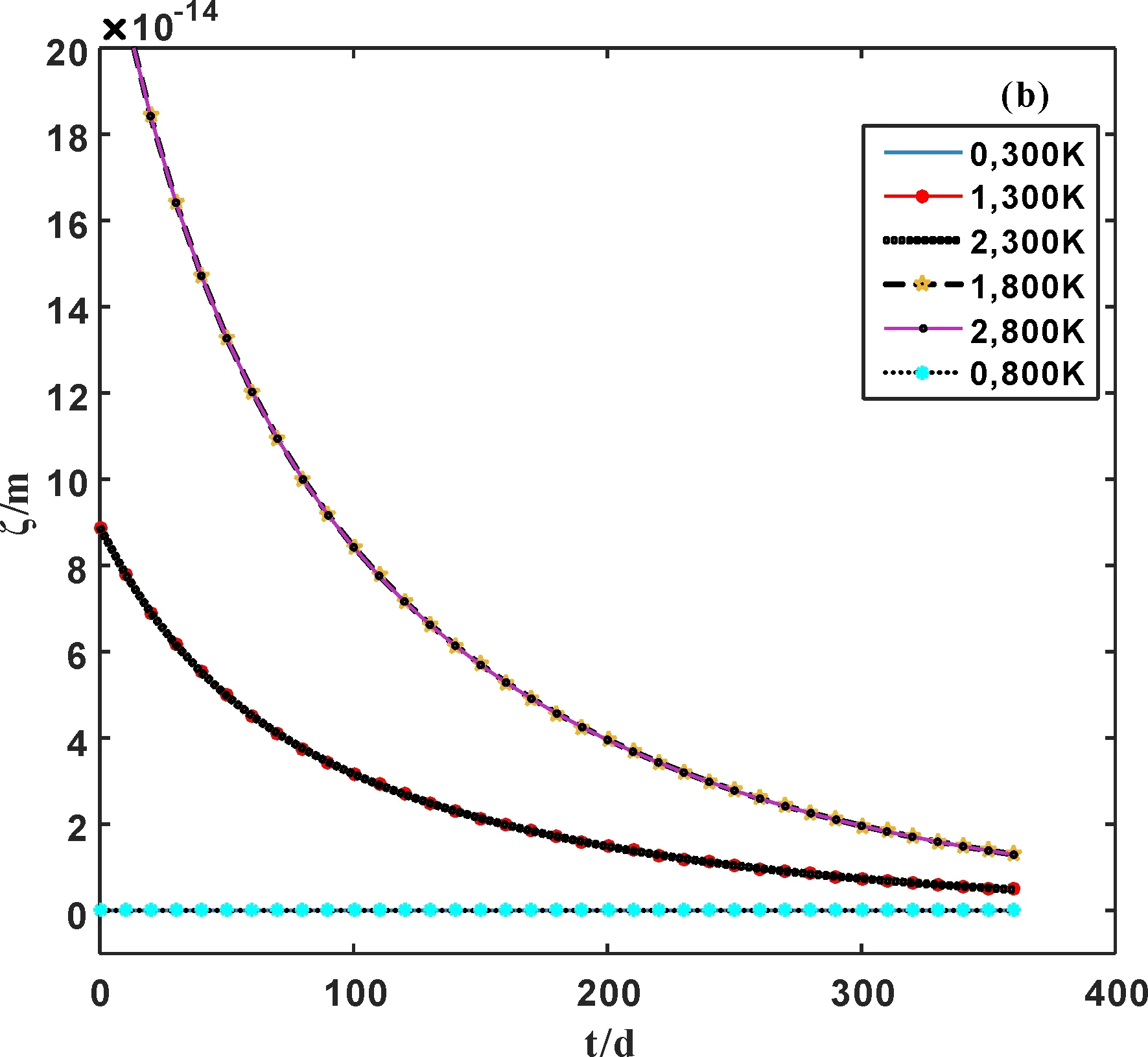
图4 原子平均位移随温度(a)和时间(b)的变化Fig.4 Variations of the average atomic displacement with temperature (a) and time (b)

由(14)式得到ZrO2热膨胀系数随温度和时间的变化见图5(a)、(b).图中曲线0、1、2的含义同图2.为了比较，图5(c)给出文[13]给出处于四方相氧化锆ZrO2的热膨胀系数随温度的变化.

由图5看出：(1)简谐近似下，ZrO2热膨胀系数不随温度和时间而变化；(2)考虑到非简谐效应后，热膨胀系数随温度的升高而减小，但变化较小，如在温度从T=300 K变化到T=1200 K，热膨胀系数由1.246×10-6K-1减小到1.244×10-6K-1，减小了0.16 %；且同时考虑第一、二非简谐的值小于只考虑第一非简谐的值，但差值较小；(3)考虑到非简谐效应后，热膨胀系数随时间近线性减小;(4)单斜相ZrO2的热膨胀系数小于同温度下四方相的值，但量级相同.

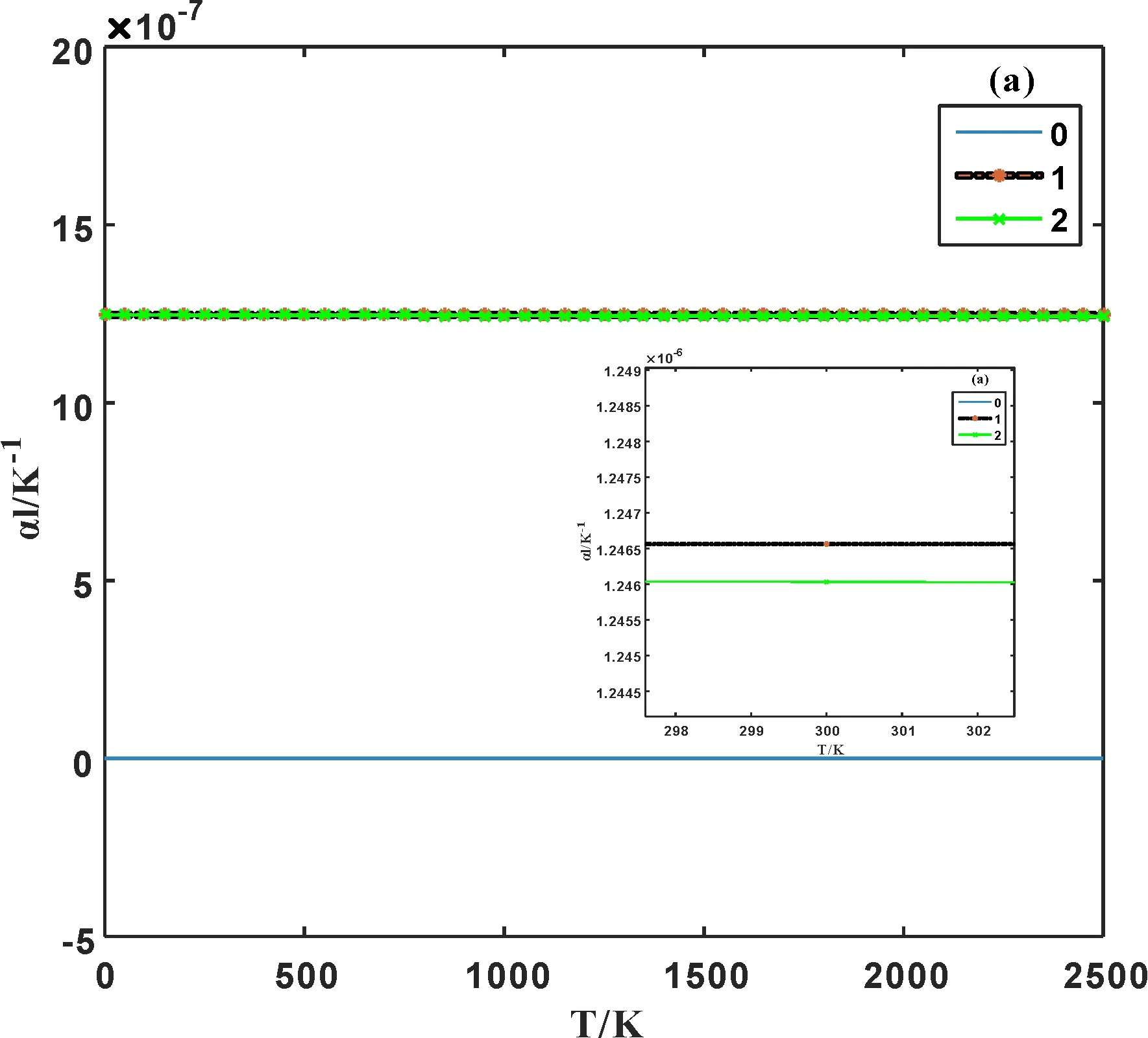
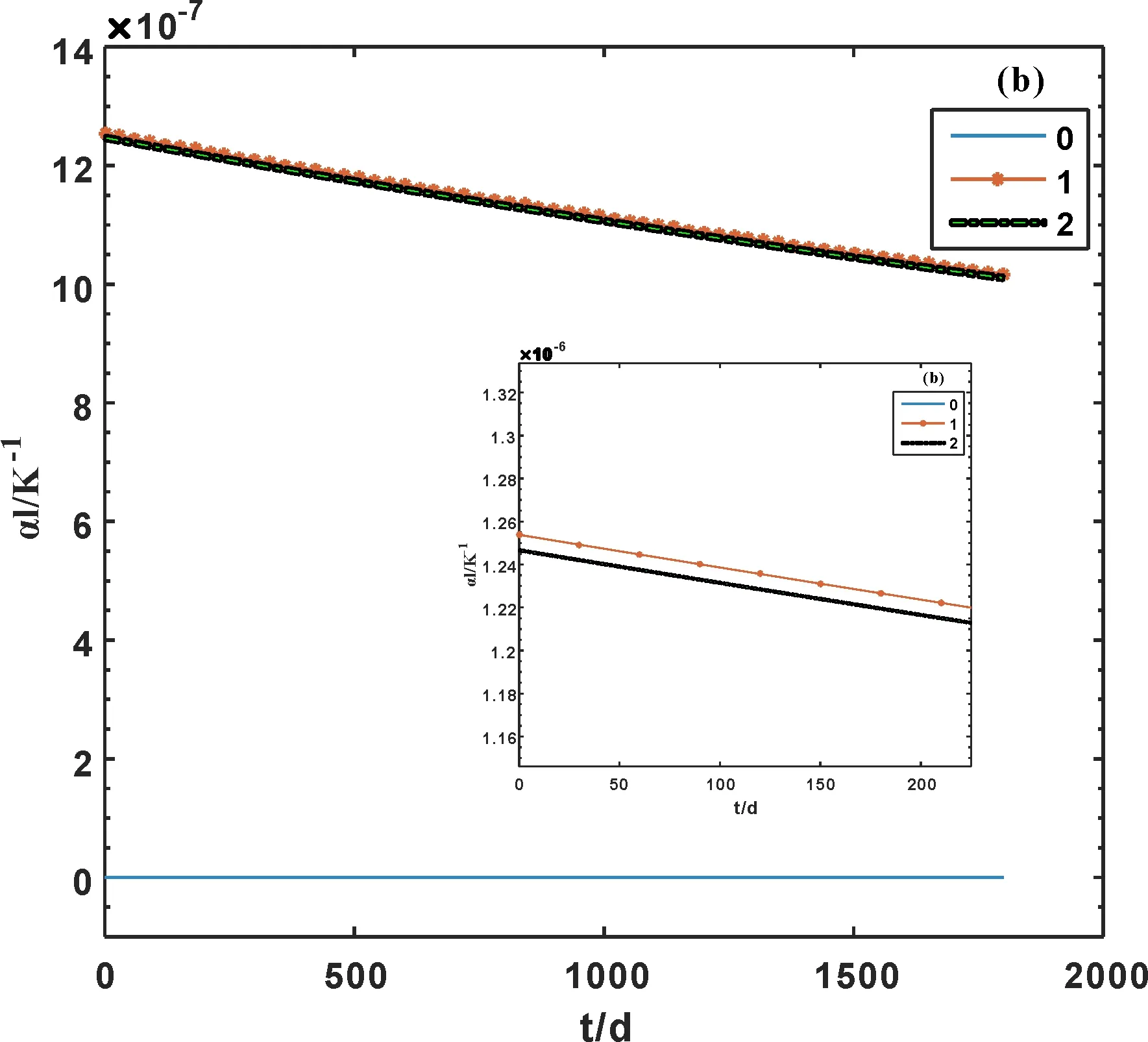
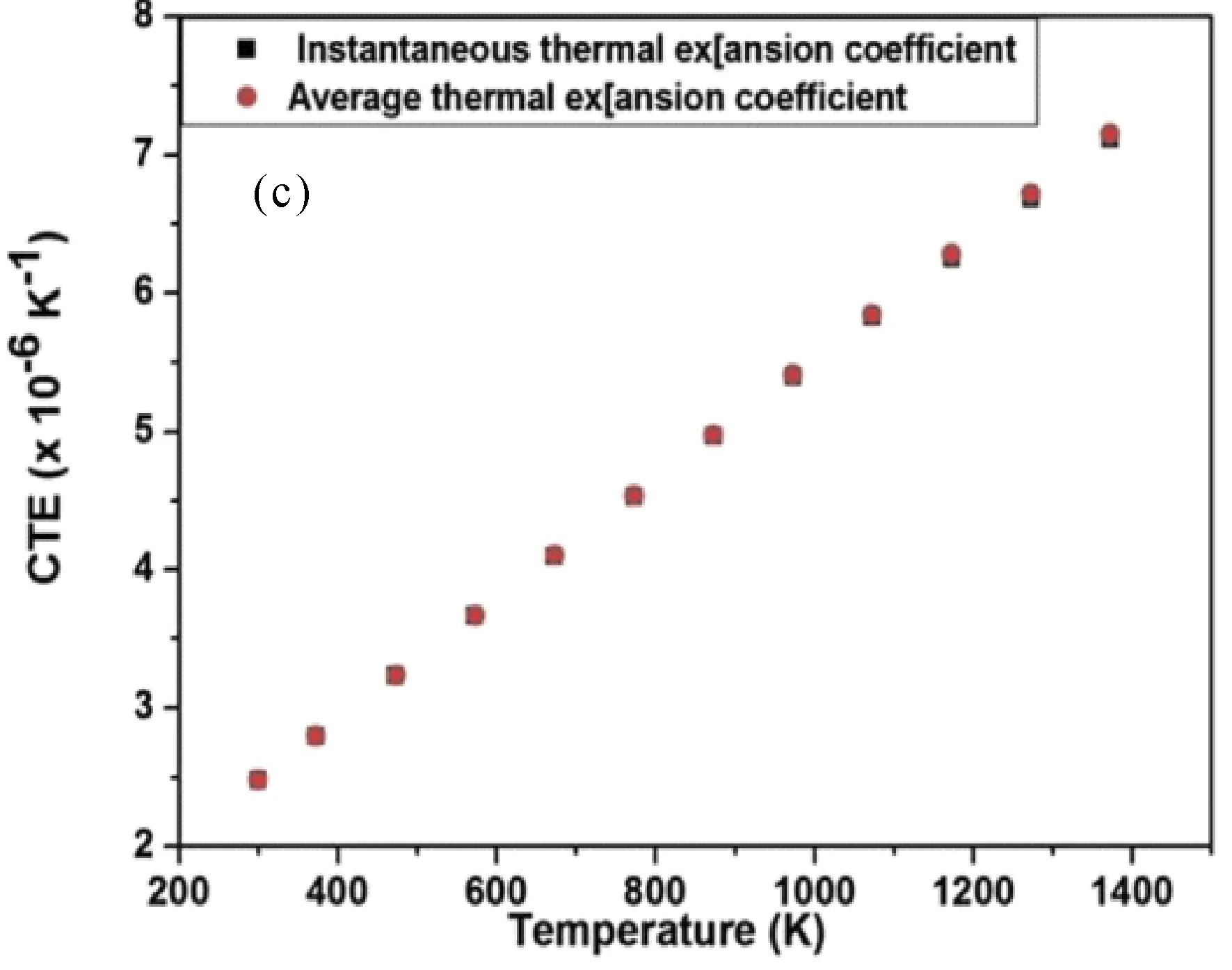
图5 单斜相ZrO2热膨胀系数随温度 (a)、时间(b)的变化和四方相热膨胀系数随 (c)随温度的变化[4]Fig. 5 Changes of thermal expansion coefficient of monoclinic phase ZrO2 with temperature (a), time (b) and that of tetragonal phase with temperature (c)

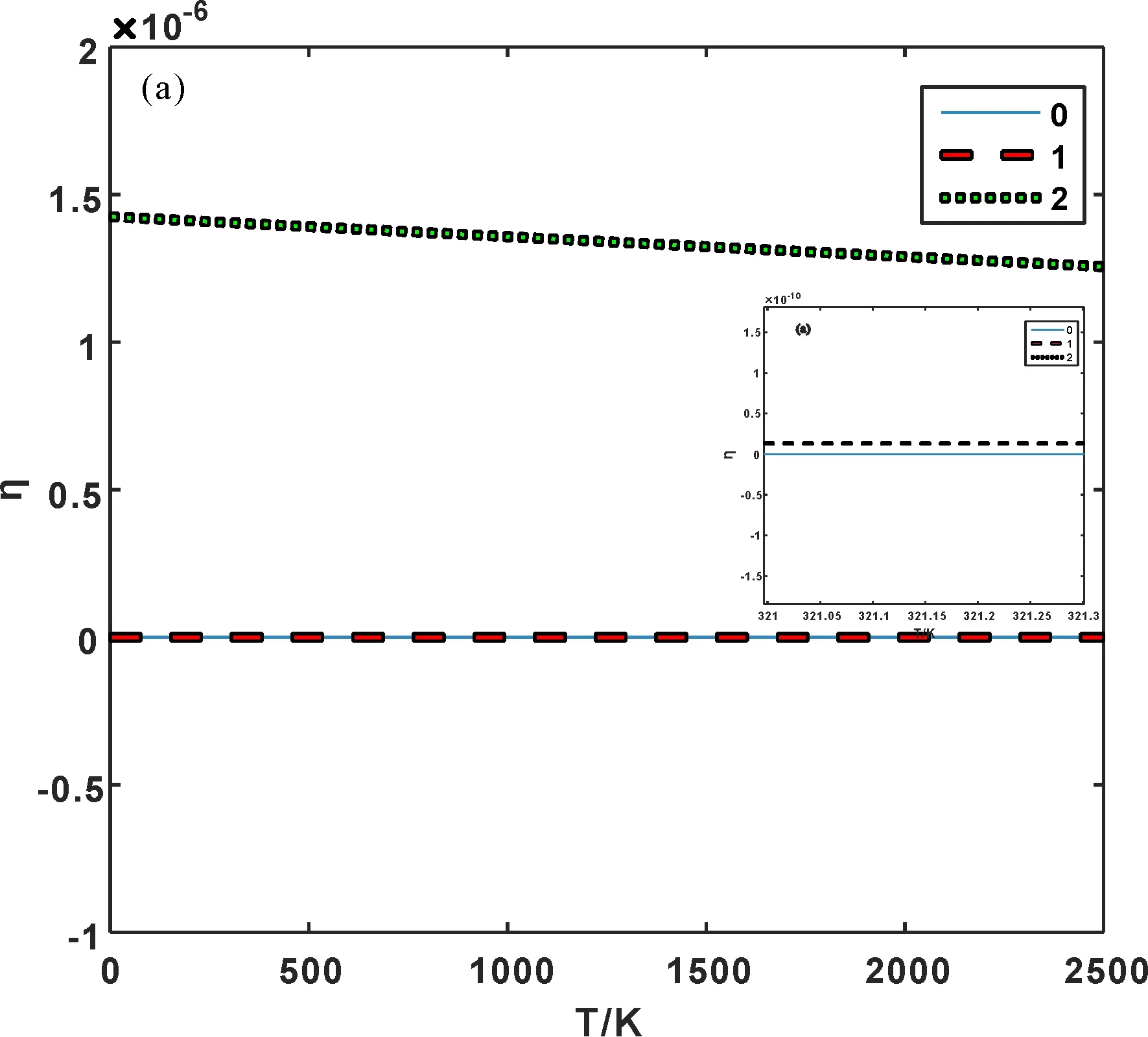
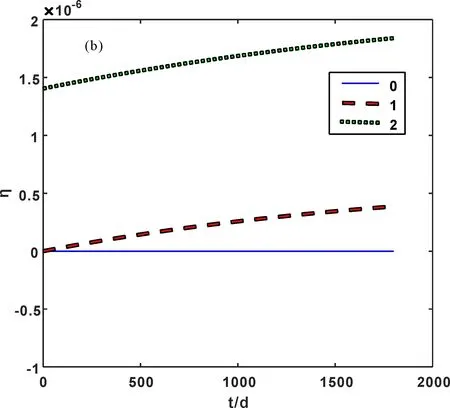
图6 ZrO2热膨胀性能温度稳定性系数随温度(a)和时间(b)的变化Fig. 6 Changes of temperature stability coefficient of thermal expansion of ZrO2 with temperature (a) and time (b)

由(14)、(15)式得到热膨胀性能温度稳定性系数随温度和时间的变化见图6(a)、(b).由图6看出：(1)简谐近似下，热膨胀性能温度稳定性系数不随温度和时间的变化而变化；(2)考虑到非简谐效应后，热膨胀性能温度稳定性系数随温度的升高而减小，其中同时考虑到第一、二非简谐项后，变化较为显著，如温度T=300 K时，热膨胀性能温度稳定性系数为1.405×10-6K-1，而只考虑第一非简谐项的结果为1.35×10-11K-1；(3)考虑到非简谐效应后，热膨胀性能温度稳定性系数随时间的而非线性增大，且同时考虑第一、二非简谐的值大于只考虑第一非简谐的结果，时间越长，简谐与非简谐的差值越大，即非简谐效应越显著.

6 结 论

研究氧传感器电解质材料原子振动特点和热膨胀系数及其热稳定性随温度和时间的变化规律，以ZrO2固体电解质材料为例，探讨原子非简谐振动的影响.结果表明：(1)简谐近似下，原子振动频率为常量；考虑到非简谐效应后，原子振动频率随温度的升高而线性增大，且温度越高，非简谐效应对原子振动频率的影响越大；(2)简谐近似下，原子振动阻尼系数为常量；考虑到非简谐效应后，原子振动阻尼系数随温度的升高而线性增大，且温度越高，简谐与非简谐的差值越大；(3)简谐近似下，原子平均位移不随温度和时间变化；考虑到非简谐效应后，原子平均位移随温度的升高而线性增大，且同时考虑第一、二非简谐的值小于只考虑第一非简谐的值，但差值较小；考虑到非简谐效应后，原子平均位移随时间非线性减小，且时间越长与简谐近似结果越相近；(4)简谐近似下，ZrO2热膨胀系数不随温度和时间而变化；考虑到非简谐效应后，热膨胀系数随温度的升高、时间的增长而减小，但随温度变化较小，如在温度从T=300 K变化到T=1200 K，热膨胀系数由1.246×10-6K-1减小为1.244×10-6K-1，减小了0.16%；(5)单斜相ZrO2的热膨胀系数小于同温度下四方相的值，但量级相同；(6)简谐近似下，热膨胀性能温度稳定性系数不随温度和时间的变化而变化；考虑到非简谐效应后，热膨胀性能温度稳定性系数随温度的升高而减小，随时间的增长而增大，其中同时考虑到第一、二非简谐项后，变化较为显著，这表明：温度越高，时间越短，ZrO2热膨胀系数的稳定性越好.