基于无人机航测技术的道路交叉口空间信息提取方法
王伟娜
(上海城建职业学院,上海310110)
0 引言
与载人飞机相比,无人机因其自身具有的重量小、机动性强和耗资少等优势,在实际中得到了广泛应用[1]。无人机进入灾难现场或者战场时,可利用自身优势对危险区域进行监视与监控,并且自动收集数据、地理或位置信息,甚至攻击数据[2]。因此,无人机在民用和军用中的应用更加广泛,如在军事应用方面,无人机可以更好地完成电子干扰、环境侦查以及相关监视等任务;在民事应用方面,无人机可以达到相关的航测、气象监测以及低空影像采集等多种目标。
由于道路交叉口是事故的多发地段,因此可以通过提取道路交叉口空间信息,实现更好的交通规划等。李康等[3]提出基于无人机大场景序列的数据自动采集方法。该方法为了实现空间数据采集与信息提取的相关目标,设计了一个基础模块,即无人机自动控制模块,并根据研究区域的实际情况设计无人机航线以及拍摄坐标,通过计算机可视化技术对无人机工作过程实现全面监控,以此提取无人机采集到的信息,实现空间数据采集与信息提取,但该方法无法通过转换四元素与欧拉角的信息获取精准位置,导致信息提取准确率过低。陈隆等[4]提出基于无人机倾斜摄影与三维实景建模空间数据采集方法。该方法对无人机倾斜摄影测量系统进行了详细剖析,并利用该技术采集空间数据,在此基础上利用采集的数据构建了三维模型,实现无人机空间信息提取,但该方法采集所需信息较少,造成空间信息提取的时间过长。
为了解决上述方法中存在的问题,提出基于无人机航测技术的道路交叉口空间信息提取方法。通过扩展卡尔曼滤波构建系统方程,准确对无人机进行定位,采集无人机航测信息,并根据所得信息构建道路交叉口空间三维模型,以此达到提高航测数据挖掘准确率,缩短了信息提取时间的最终目标。
1 卡尔曼滤波的扩展
1.1 无人机非线性模型
通过下列方程式表示无人机非线性模型[5],即
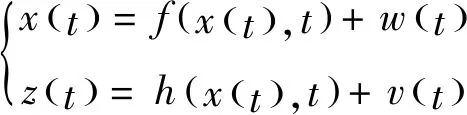
(1)
x(t)和z(t)分别为无人机状态变量;f(x(t),t)与h(x(t),t)分别为导航方程和观测方程;w(t)与v(t)分别为噪声向量以及观测噪声。
此时,无人机飞行时状态为
X=[x,y,z,u,v,w,q0,q1,q2,q3,g]T
(2)
(x,y,z)为在导航路线中的无人机位置信息;(u,v,w)为无人机在当前位置的速度;(q0,q1,q2,q3)分别为无人机姿态角;g为重力加速度。
1.2 无人机导航方程的推导
在上述分析基础上,本文通过推导系统导航INS得到无人机导航方程[6]。
1.2.1 姿态角变化率
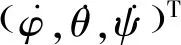
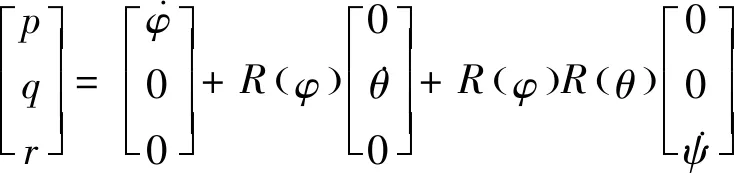
(3)
(4)
1.2.2 无人机数据采集
利用IMU可获取无人机飞行过程中由于旋转产生的向心加速度、重力加速度和速度。因此,结合该结果可以实现对于无人机加速度的精准计算[7]。
假设在无人机坐标系中,加速度向量与重力向量分别为(ax,ay,az)T和(gx,gy,gz)T,机体线速度与角速度和向心加速度有关,得到
(5)

1.2.3 位置变化率
通过加速度一次积分得到无人机运行速度,此时2次得到位置值为

(6)
则位置变化率与欧拉角与四元素的关系为
(7)
2 道路交叉口空间信息提取
利用最小二乘法计算近似解,将平面坐标观测值共线方程进行迭代,计算最佳数值。三维重建精度可以通过光束法平差进行提升,任选一张图像作为单元,测量该图像像素点坐标,并通过共线方程式列出数据采集结果误差方程,获得加密点近似值的坐标与外方位元素,以此达到数据采集结果修正的相关研究目标。在此基础上利用采集到的信息构建道路交叉口空间三维模型,实现道路交叉口空间信息提取。
2.1 数据采集结果修正
假设(X,Y,Z)与(XS,YS,ZS)分别为世界坐标系以及相机坐标系;S为无人机摄影中心;M与m分别为相机坐标系上的一点以及摄影节点;(Xm,Ym,Zm)为无人机航测过程中的空间辅助坐标。已知S,m,M三点共式,利用平面坐标与空间辅助坐标相像的关系可解出共线方程式:
x-x0=
(8)
y-y0=
(9)
x0、y0和f为影像的内方位元素,与平面中心点和摄像机主距相像。
得知共线方程的线性化,将其展开并列为:
(10)
(11)
dXS、dYS、dZS、dφ、dω和dκ为外方位元素的修正结果;Fx0和Fy0为该方程的近似值;dX、dY和dZ为坐标修正结果。
2.2 实现空间信息提取
假设无人机航测数据采集过程中,P为航测数据采集过程中所允许的误差,则无人机航测数据采集误差最小化方程为
(12)
对上述仿真进行消元处理,即可获取无人机航测数据误差校正结果。
根据无人机飞行路线规划定义拍摄图像、拍摄高度和间隔等参数,并将同名点之间重复图像,根据图像测量原理与之匹配,利用获得的点云密集点构建道路交叉口空间的三维网络模型[8]。
多边形网络模型由带有三维坐标信息三维点云构建,展现模型最真实的形态特点。可利用多边形网络模型获取物体不规则形态与物体多面体的形状特点。在原有三维坐标点云基础上,利用高分辨率影像,构建显示物体形态的三维多边形网格,以此完成道路交叉口空间的三维模型构建,利用该模型提取道路交叉口空间信息,以此达到相关的研究目标。
3 实验分析
为了验证基于无人机航测技术的道路交叉口空间信息提取方法的有效性,需要对航测无人机的空间信息进行自动提取,并验证其有效性。实验环境由MATLAB 7.1仿真软件构建,并根据Visual C++6.0对实验程序进行编写。
分别采用无人机道路交叉口空间数据自动采集方法、基于无人机大场景序列的数据自动采集方法(方法1)和无人机倾斜摄影测量的地理空间数据采集(方法2)进行位置信息测试,测试结果如图1所示。

图1 各方法的位置信息
通过图1中数据得知,本文方法的无人机飞行位置与实际测量值极为接近,而方法1和方法2获取的无人机飞行位置角度存在过高和过低的问题。相比之下,本文方法的无人机飞行位置定位效果更好,这是由于该方法通过用卡尔曼滤波推导出观测方程与状态方程,准确获得无人机的位置信息,实现无人机的精准定位。
在上述实验的基础上,为进一步验证不同方法的实际应用效果,进行了道路交叉口空间信息提取准确率比较。
假设无人机工作过程中,在正常信息中会掺杂一定的异常信息,这部分信息用{a1,a2,…,an}表示,其数量为n,则{b1,b2,…,bm}为异常信息对应属性构成。随机在异常信息中选择1组数据ap,此类型信息特征向量用bq描述。
不同算法性能高低可根据运行中无人机航测数据库中所挖掘的异常信息是否准确进行判断。所以在进行道路交叉口空间信息提取过程中,需要对无人机航测数据挖掘准确率进行判断,具体描述为
(13)
分别采用本文方法、方法1和方法2,对道路交叉口空间信息提取过程中的无人机航测数据挖掘准确率进行测试,测试结果如图2所示。
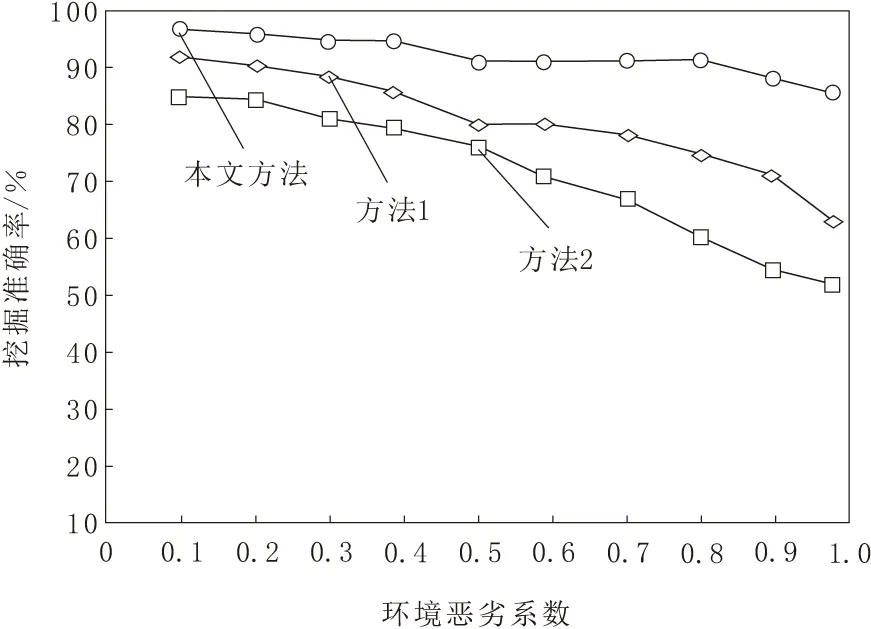
图2 不同方法的挖掘准确率
根据图2中数据可知,随着环境恶劣系数的增加,方法1与方法2的挖掘准确率在逐渐下降,而本文方法的挖掘准确率始终高于方法1和方法2。这是由于基于无人机航测技术的道路交叉口空间信息提取方法通过卡尔曼滤波列出方程矩阵,确定无人机的位置信息,以此采集无人机航测数据,可以有效提高挖掘准确率。
分别采用本文方法、方法1和方法2对道路交叉口空间信息提取时间进行测试,测试结果如图3 所示。
分析图3实验数据得知,随着环境恶劣系数的增加,不同方法的道路交叉口空间信息提取时间也在不断增多,但本文方法的道路交叉口空间信息提取时间始终低于方法1和方法2,验证了所提方法对道路交叉口空间信息提取的速度较快。
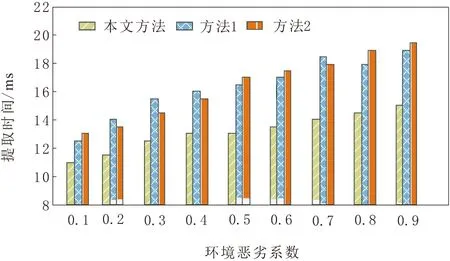
图3 不同方法的挖掘时间
4 结束语
随着无人机小型化和智能化的发展,该行业与现实应用结合越来越密切,但是利用无人机进行地理位置观测、监测和数据传输仍存在不足,阻碍无人机对数据采集。为此进行了基于无人机航测技术的道路交叉口空间信息提取研究。通过推导卡尔曼滤波获得状态方程与观测方程,以此监测无人机位置,利用无人机采集数据信息建立道路交叉口空间三维建模,实现了道路交叉口空间信息提取,促进了无人机在数据采集以及信息提取领域中的进一步发展。

