基于ANSYS的自动扶梯桁架结构分析及实验研究*

杨天玲，朱道林,张海波,黄金永

(1.浙江机电职业技术学院 智能制造学院,浙江 杭州 310053;2.浙江新联民爆器材有限公司，浙江 杭州 310011;3.杭州西奥电梯现代化更新有限公司,浙江 杭州 311102)

0 引 言

自动扶梯的金属桁架是整个扶梯的承重结构,其强度和挠度直接影响自动扶梯的正常运行。但在GB16899—2011[1]和EN115—1:2017[2]标准中,却只规定了自动扶梯的金属结构架的挠度要求:自动扶梯或自动人行道的自重加上5 000 N/m2的载荷,计算或实测的最大挠度,不应大于支撑距离的1/750;对于公共交通型自动扶梯和自动人行道,最大挠度不应大于支撑距离的1/1 000。

但在上述标准中,对如何验证是否满足该标准没有做进一步的规定。标准中对自动扶梯桁架只有挠度要求。但实际上还必须要考虑,整个桁架结构的应力水平是否在材料许用的应力范围内,以及上弦杆受压的稳定性问题。

在GB50017—2017[3]10、DIN18800—T1[4]、DIN18800—T2[5]标准中,虽然对类似钢结构计算给出了经验性的理论计算方法,但是需要大量繁琐的手动计算。

朱昌明[6]简述了自动扶梯桁架计算的基本理论,但其未对该理论进行细化分析。高原[7]分析了船用自动扶梯在各种晃动工况下的结构强度问题,但是该种工况不同于一般场合的扶梯使用工况。郭玮[8]采用ANSYS有限元方法,对某密封结构进行了仿真研究,并采用实体模型进行了建模分析;但是该结构不同于桁架的薄壁结构。王肖英[9]采用ANSYS方法对某传动轴结构进行了静力学分析,同样也采用了实体模型。在对桥梁结构进行分析时,白鸿宇[10]主要采用了拓扑优化模块。在对自动扶梯桁架挠度进行分析时,周游[11]只是基于ANSYS,分析了型材偏差对桁架挠度的影响。方晓旻[12]对自动扶梯金属结构轻量化方法进行了研究,但其未对标准基本要求展开研究。LIANG J[13]采用RFEM软件,对自动扶梯的桁架结构进行了分析;但是因为其采用的是手动建模方式,较难以实现快捷的参数化分析。XIAOWEI Y[14]应用C++语言二次开发ANSYS,对自动扶梯桁架的稳定性进行了分析。

针对自动扶梯桁架在各种工况下所受载荷特征,笔者利用ANSYS软件APDL语言进行参数化建模、约束、施加载荷,并求解不同工况条件下的最大位移和最大应力,校核整体及受压杆件的稳定性,对其薄弱部位进行优化设计,使其满足标准要求。

1 有限元理论基础

在分析比较复杂的变形受力问题方面,有限元分析方法有着非常广泛的应用。

在自动扶梯桁架结构中,通常采用的构件都是薄壁型材,且限制在材料的线弹性范围内。因此,笔者在此使用考虑剪切变形的梁单元BEAM189[15-17]。

针对该模型,根据胡克定理,一个单元节点位移和受力变换如下:

[F]e=[K]e[u]e

(1)

式中:[K]e—单元刚度矩阵,N/m;[u]e—单元节点位移,mm;[F]e—单元载荷矩阵,N。

根据3D梁单元BEAM189特性可知,一个单元节点受力方程扩展到任意节点的力与位移关系如下式所示:

(2)

式中:i,j,m—BEAM 189单元线弹性范围内3个自由度。

对于桁架模型,笔者通过单元位移矩阵的传递,借助有限元的离散方法,引入位移边界条件,将单元边界的载荷等效作用到节点上,以此通过求解,得到每个节点的位移和受力情况。

2 自动扶梯桁架载荷工况

自动扶梯基础参数如下:

提升高度5 300 mm,水平跨距15 000 mm,倾斜角度30°,上平层长度3 240 mm,下平层长度2 294 mm;无中间支撑。

基本参数示意图如图1所示。

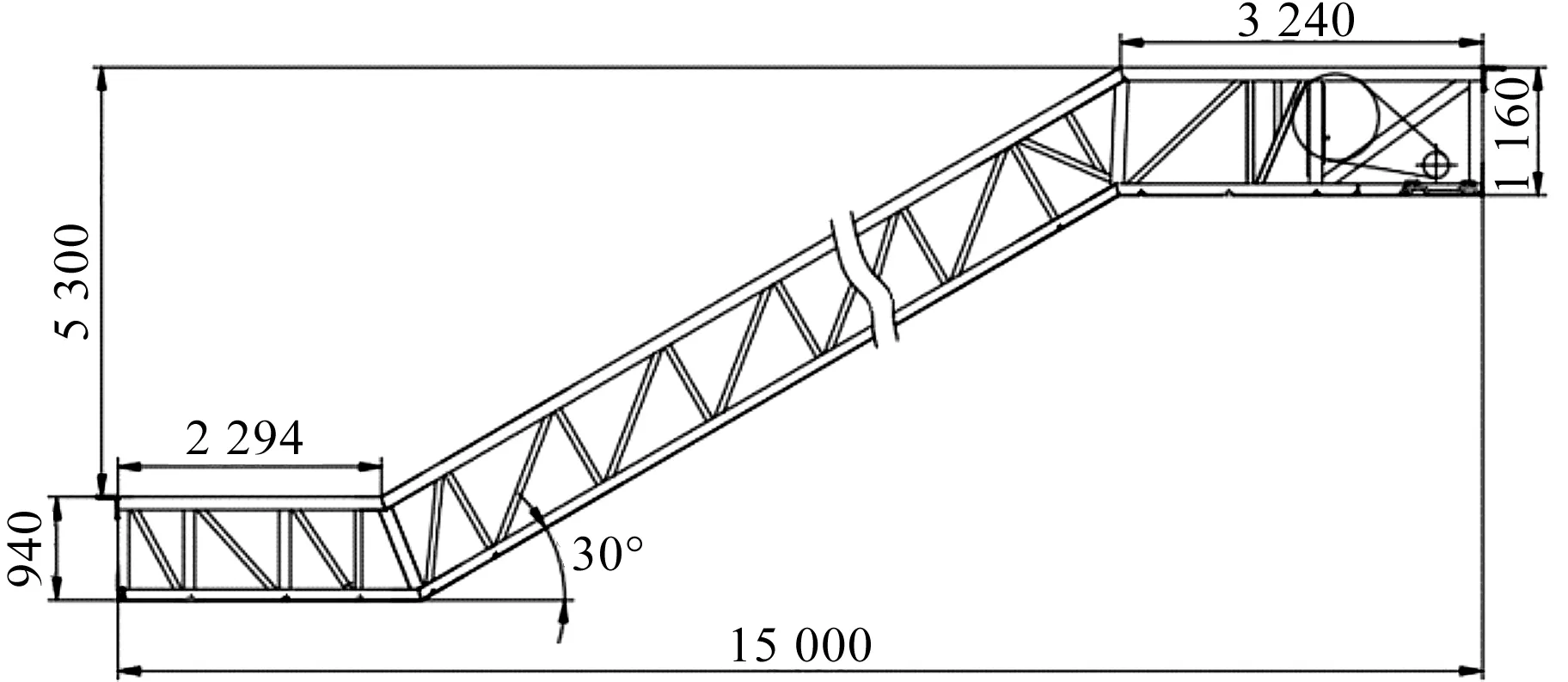
图1 基本参数示意图

2.1 自动扶梯桁架构造

自动扶梯的金属桁架结构主要由上下弦杆、斜腹杆、竖杆、中间横梁、底板等组成,通过焊接的方式,将其连接成整体的结构架。其中,上下弦杆、斜腹杆、竖杆都采用方管型材,中间横梁采用槽钢。

因为上平层安装有主机、主驱动系统、扶手系统等,下平层安装有转向机构和梯路张紧系统,所以要对上、下平层的斜腹杆和竖杆结构进行相应的加固。

自动扶梯桁架截面型材如表1所示。

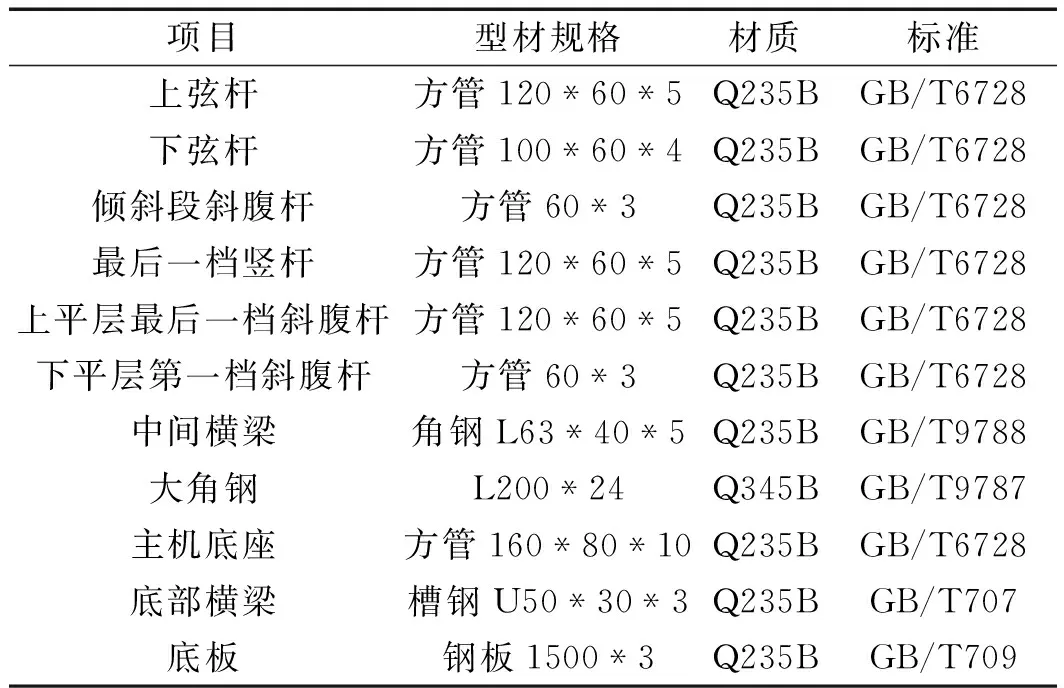
表1 自动扶梯桁架截面型材

桁架截面示意图如图2所示(图中标明各杆件名称及位置)。

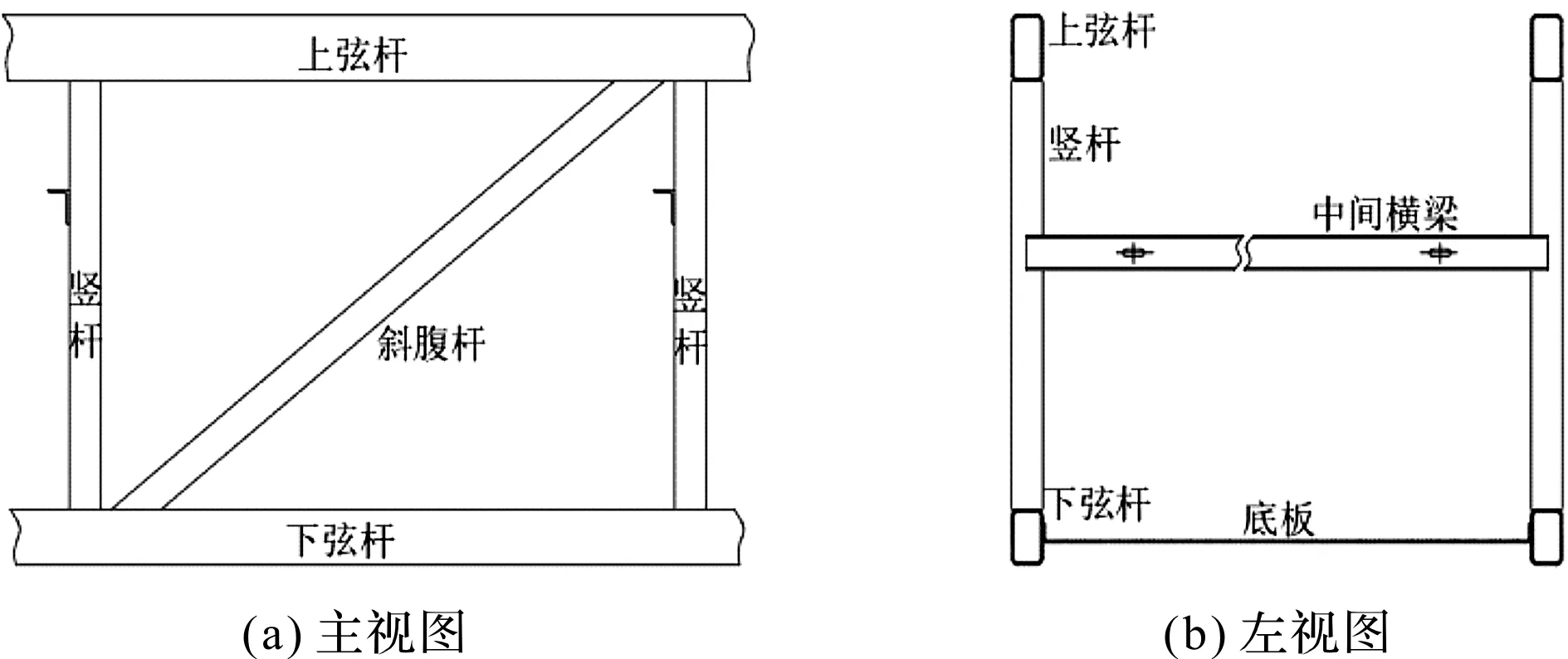
图2 桁架截面示意图

2.2 桁架建模简化

在桁架结构中,笔者针对所有杆件的每一个交叉点都建立一个节点,并按照实际结构连接顺序,将节点连接成线和面,最后构成整个金属桁架的有限元模型,如图3所示。

图3 金属桁架有限元模型

由于桁架结构中所用的型材都是薄壁结构,长度远超过截面尺寸参数,在简化模型时,笔者采用ANSYS专用BEAM189梁单元,底板采用SHELL181壳单元,并赋予材料属性[18]。

材料属性APDL程序语言如下:

……

ET,1,BEAM189

MP,DENS,1,7.85E-6

MP,EX,1,2.06E5

MP,PRXY,1,0.3

ET,2,SHELL181

MP,DENS,2,7.85E-6

MP,EX,2,2.06E5

MP,PRXY,2,0.3

……

在模型完成后,再进行约束。

自动扶梯实际安装结构非常类似简支梁。无支撑桁架约束简图如图4所示。

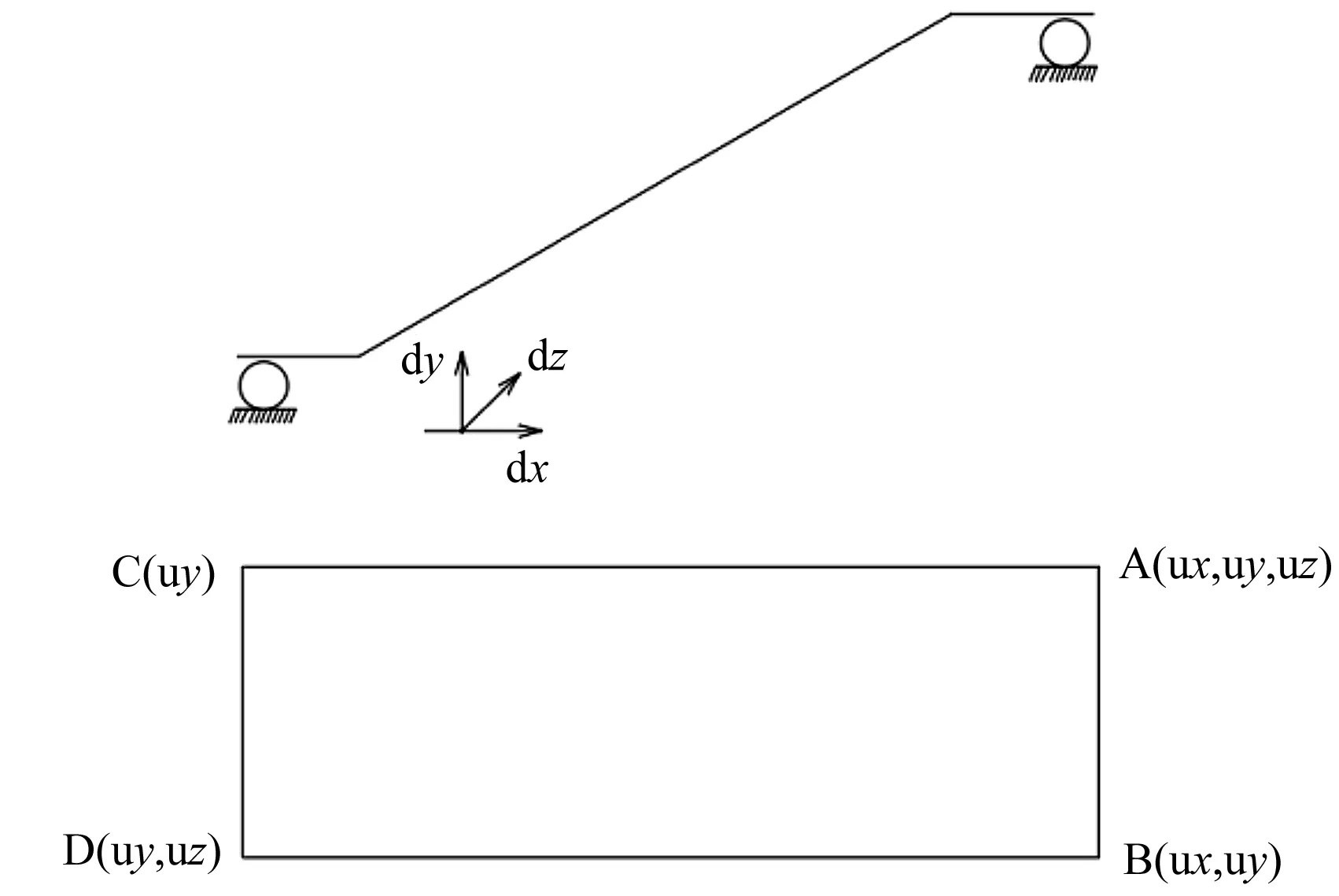
图4 无支撑桁架约束简图

2.3 载荷工况

由于桁架承载了自动扶梯上所有的载荷,包括桁架自身的重量,根据GB50017—2017,在计算钢结构强度时,静态载荷载荷系数取1.35,动态载荷载荷系数取1.5。

组合工况及其用途如表2所示。

表2 组合工况及其用途

APDL语言编写程序时,采用多层嵌套循环,有利于简化程序。例如:

(1)上弦杆模型程序:

……

*DO,I,0,N1

K,NL+1+I,651+1160*I,0

K,NL+101+I,651+1160*I,-HSYSIS

KBETW,NL+1+I,NL+101+I,NL+201+I,DIST,TBIS

*ENDDO

……

(2)扶手系统重量加载程序:

*DO,I,0,1

*GET,LENG_PR,LINE,2,LENG

美国通用电气公司是世界上最大的电器和电子设备制造公司，是《财富》杂志连续4次选出的“全美最受推崇的公司”，也曾连续多年被评为500强之首。美国通用电气公司自1892年成立至今，已经成为一家集科技、传媒、金融服务于一身的多元化经营的国际公司。尽管通用电气公司业务复杂且庞大，但这并没有成为通用电气公司前进的绊脚石。这个“百年老店”能够长盛不衰，与其卓越的人力资源管理密不可分。

*SET,HAND1,LENG_PR*HANDRAIL/4000

FK,2+I*OFFSNUM,FY,-HAND1

*ENDDO

……

2.4 模拟计算结果

根据组合工况一,通过计算可以得到桁架的最大挠度fmax=11.462 mm。由于GB16899—2011标准要求fmax=水平跨距15 000/1 000=15 mm。由此可见,该结果满足标准要求。

组合工况一挠度云图如图5所示。

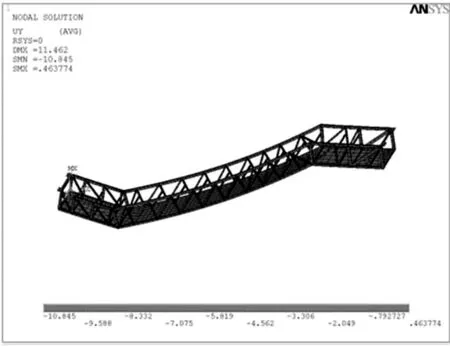
图5 组合工况1挠度云图

组合工况二SEQV应力云图如图6所示。

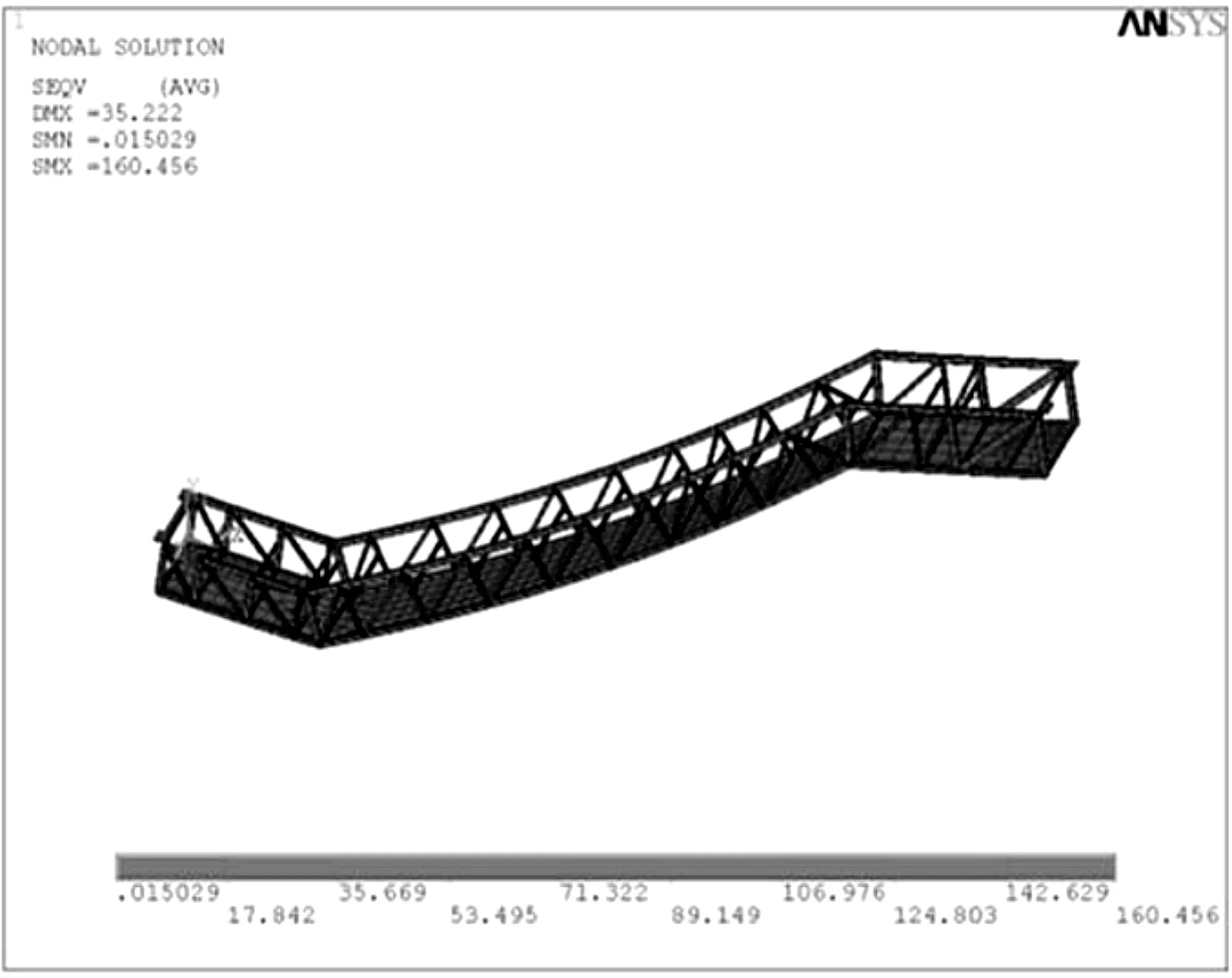
图6 组合工况二SEQV应力云图

根据组合工况二,通过计算可以得到最大应力为σmax=160.46 MPa。

该最大应力满足材料使用标准,即:

σmax<σs

(3)

式中:σs—材料许用应力,σs=235 MPa。

针对上弦杆,由于其主要受压力的作用,还要验算其稳定性。

在构件受压、扭转屈曲状态时,根据如下公式进行验算[3]35:

(4)

式中:N—模拟计算中得到最大轴向力,N;Mx,My—模拟计算中得到x、y向弯矩,N·mm;rx,ry—截面塑性发展系数,封闭截面取1.05;Mplx,Mply—材料绕x轴、y轴许用弯矩,N·mm;A—材料截面积,mm2;f—材料许用抗弯强度,N/mm2。

通过计算可得到其值基本接近于1,符合等效构件弯曲极限状态的许用要求。该结果表明,在最严苛载荷工况条件下,材料的使用率可达到最高。

3 实验验证

接下来,笔者通过挠度测试数据对仿真结果进行验证。

按照GB16899标准中挠度要求,乘客载荷5 000 N/m2时,测量得到的最大变形即为挠度值。按照该载荷密度,笔者将标准砝码(25 kg/个)放置在梯级和楼层板上。

乘客载荷加载图如图7所示。

图7 乘客载荷加载图

按照自动扶梯新检规TSGT7005—2012[19],挠度实验方法如下:

自动扶梯安装好后,设置合理数量挠度测量点(5个及以上测量点),用铅锤法先测量其初始变形量,并记录。

根据简支梁均布载荷受力情况,最大挠度分布在中间靠上的位置上。

笔者在该自动扶梯上共设置了7个测量点,其中3个点密集分布在最大挠度附近,可以拟合该桁架的实测挠度曲线。

乘客载荷示意图如图8所示。

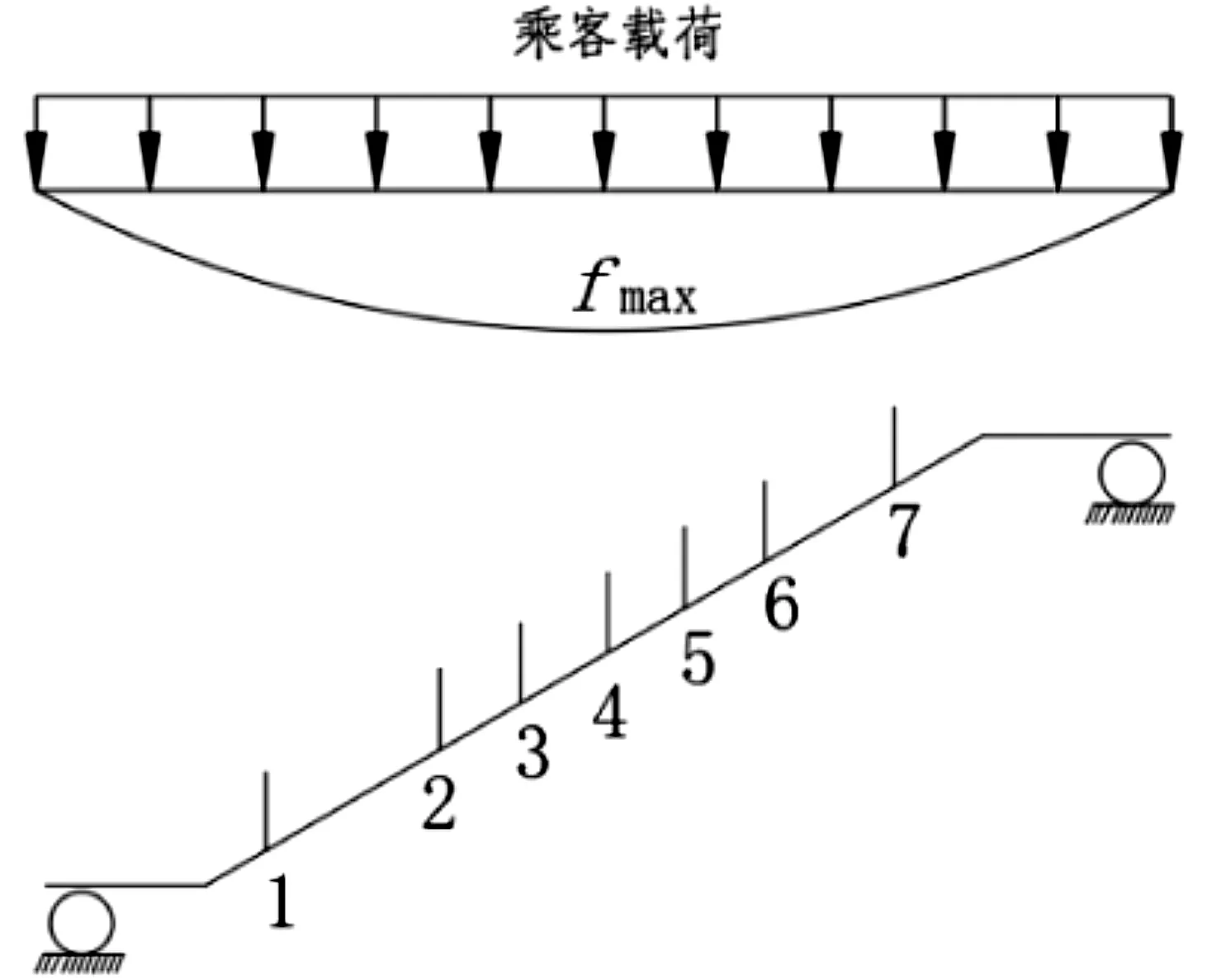
图8 乘客载荷示意图

这些测量点也是仿真模型中建立节点的位置,便于将实测值和模拟值进行比较。笔者在楼层板、梯级上按照标准5 000 N/m2施加载荷,加载10 min后,记录桁架上各点变形量,后一变形量与初始变形量的差值即为乘客载荷引起的挠度值。

仿真模拟值和实测值的对比结果如表3所示。

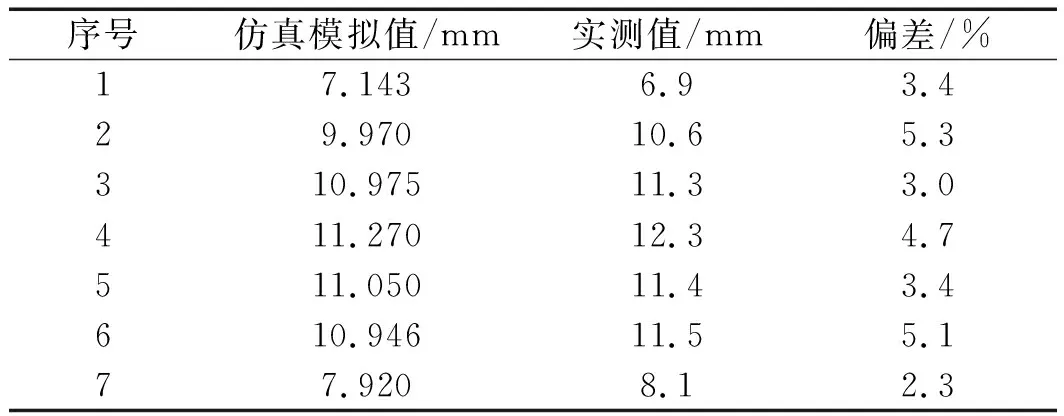
表3 仿真模拟值和实测值对比

从表3可以看出:

仿真模拟值与实测值偏差仅5%左右,两者非常相近,这说明该建模、约束、加载的方式符合自动扶梯桁架的实际情况,计算方法精确度比较高;

点2～7实测值大于模拟值,主要是因为集中载荷大部分位于整体桁架偏上部的位置。

存在这些偏差的原因是:(1)模拟计算中采用的型材截面都是理论截面,而实际型材尺寸往往都是下偏差;(2)桁架实际是焊接连接,模拟计算时杆件相互之间都是固定连接的,连接方式不同也有误差存在。

自动扶梯挠度仿真模拟值和实测值对比图如图9所示。

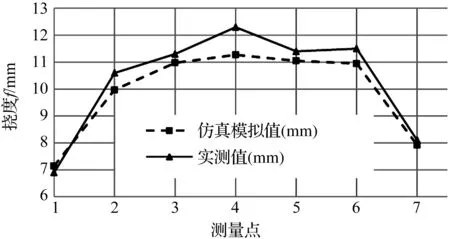
图9 仿真模拟值和实测值对比图

由图9的对比图可以看出:两者曲线走势比较吻合,且两者挠度达到最大值的位置都是在桁架中点偏上的点4处。

4 结束语

为了对自动扶梯的桁架进行受力分析,笔者采用ANSYS软件,对自动扶梯桁架各种工况载荷进行了静力学分析,应用APDL语言编程方式对其挠度、应力及稳定性进行了分析,并通过挠度测试数据对仿真结果进行了验证。

研究结果表明:

(1)APDL编程方式参数化程度高,通过输入不同参数值就可以计算各类桁架结构,为类似桁架类结构的计算分析提供一种可借鉴的参考方法,节约了大量实验时间;

(2)自动扶梯挠度仿真模拟值和实测值偏差5%左右,两者曲线走势非常吻合,说明模拟计算可靠性比较高,具有较好的推广意义。

在下一阶段的工作中,笔者将继续深入研究和拓展此种模拟计算方法,同时研究极端工况(例如风载荷、雪载荷、地震载荷、乘客载荷分布不均等)对自动扶梯桁架强度的影响。

由于上述这些特殊工况与标准中要求的工况有较大差异,在今后的研究中,可能需要进一步优化和改进计算方法,并设计相关实验,以实现对特殊工况的更好模拟。