基于变模式提取与去趋势波动分析的液压泵故障诊断研究*

金林彩,叶杰凯,汤小明,赵 健,易灿灿

(1.丽水市特种设备检测院,浙江 丽水 323000;2.武汉科技大学 机械自动化学院,湖北 武汉 430081)

0 引 言

随着液压技术的高速发展,凭借液压元件精密度高、抗载荷和自动化等优点,目前,液压系统已被广泛应用于机床、化工和工程机械等领域。

作为液压系统的核心,液压泵是保证整个系统正常运行的关键,其健康状态将直接影响大型装备能否长期安全稳定地运行[1,2]。因此,及时迅速地对液压泵的故障进行识别,对提高液压系统运行的可靠性,降低其运行维护成本有着重要的意义。

在液压系统的故障诊断中,基于振动信号的时频分析是一种常用的检测方法。液压泵长期在变转速与变负载的工况下运行,当其发生故障时,所测得的故障振动信号往往呈现非线性和非平稳的特性,再加上还有其他强噪声等因素的干扰,因此,如何对液压泵故障进行快速、准确地识别,并提取出有效的故障特征,一直以来都是液压泵故障诊断的难点[3]。

经验模式分解(empirical mode decomposition,EMD)是HUANG N E等人[4]提出的一种多分量信号自适应分解算法,其具有正交性、完备性等优点;虽然EMD在故障诊断领域已经得到了广泛应用,但其存在模式混叠、包络拟合以及对噪声敏感性不足等问题[5,6]。JONATHAN S[7]提出了一种局域均值分解(local mean decomposition,LMD)方法,其在减少迭代次数、抑制边界效应等方面要优于EMD;不过该方法也存在不少缺点,比如算法效率低、模式混淆等。

变分模式分解(variational mode decomposition,VMD)是DRAGOMIRETSKIY K等人[8]提出的一种新的自适应分解算法。该方法通过迭代寻找变分模型最优解,将振动信号分解为一组模式分量;同时在迭代过程中,不断更新每个模式分量的中心频率和频带,从而可以对振动信号进行自适应划分[9]。

由VMD算法和基本原理可知,其分解结果受惩罚参数和分量个数的制约,且必须在开始分解之前确定模式数量。当设置模式的数量过高时,会出现一定的干扰模式,影响其对有效信息的提取;当设置模式的数量过低时,又会出现模态混叠现象[10]。

为了在液压泵振动信号中更好地提取到其微弱的故障特征,需要对信号分解方法进行优化。在VMD的基础上,研究人员又提出了一种新的模式分解算法,即变模式提取(VME)[11]。在采用VME对信号进行处理时,首先需要通过VMD将信号分解成各模式分量,然后利用Wiener滤波器对各分量进行滤波,最后根据得到的信号中心频率近似值,对中心频率附近的特定模式进行提取,且提取的该特定模式与经VMD分解后的其他模式分量无关。

与传统的VMD相比,VME消除了对分量数量的限制,具有更高的收敛速度,同时也大大降低了提取特定模式分量的计算量。因此,VME在液压泵故障诊断领域具有良好的应用前景。

近年来,有学者将非线性时间序列分析方法用于对振动信号的处理,通过提取标度指数来进行故障识别[12，13]。去趋势波动分析(DFA)是PENG C K等人[14]提出的一种计算时间序列长程相关性标度指数的方法,其优点在于可以将不同阶的外来趋势项从时间序列中去除,还原时间序列本身所具有的统计行为特征。目前,DFA在气象、金融和地震波等领域应用广泛。MOURA E P等人[15]采用DFA对齿轮故障进行了识别,达到了故障分类和降维的目的,效果十分显著。

另外,在数据降维方面,为了更好地保留局部重要几何结构的数据,有别于传统的主成分分析(principal component analysis,PCA)方法,HE X[16]提出了局部保留投影(locality preserving projection,LPP)法。该方法首先将高维度数据投影到低维子空间中,再对降维后的投影数据进行聚类分析,由此得到较好的聚类效果。在数据处理过程中,该方法不仅可以降低原始空间数据的计算复杂度,减少冗余信息对模型的干扰,还可以最大限度地保留局部数据结构中的有效信息,提高故障分类的准确率。

为此,在利用VME对信号进行模式分解的基础上,笔者提出一种基于去趋势波动分析与小波降噪的液压泵故障信号降噪和故障模式分类方法。该方法首先通过VME对原始振动信号进行分解,得到多个不同的模式分量IMFs,再对中心频率附近的特定模式分量进行提取,然后通过去趋势波动分析(DFA)方法,区分有用信号分量和噪声信号分量,最后对重构的信号进行多统计学特征计算和LPP降维,以实现对不同液压泵故障类型进行聚类分析。

1 理论描述

1.1 变模式提取算法(VME)

对于输入信号f(t),将其分解为期望模式ur(t)和剩余信号fk(t),则其表达式为:

f(t)=ur(t)+fk(t)

(1)

期望模式ur(t)应在其中心频率附近,因此,可通过最小化,得到其表达式为:

(2)

式中:δ(·)—狄拉克分布;*—卷积;ωr—中心频率;I1—期望模式的带宽。

为实现完全准确的变模式提取,此处使用具有以下频率响应的滤波器:

(3)

此外,为了使fk(t)与ur(t)之间的频谱重叠最小化,使用以下惩罚函数,即:

(4)

式中:γ(t)—所用滤波器的脉冲响应。

在满足式(1)的约束条件下,将I1和I2最小化,即:

(5)

式中:η—用于平衡I1和I2的参数。

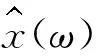
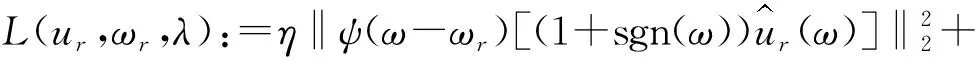
(6)

式中:λ—拉格朗日乘数。

使用乘数算法的交替方向法,即通过优化一系列迭代子,就可以解决最小化问题。第(m+1)次迭代中的期望模式函数可由以下表达式获得:

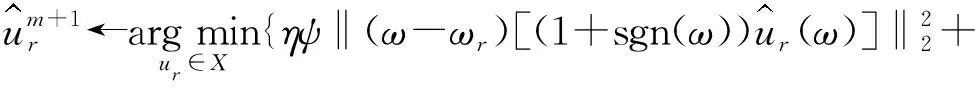
(7)

(8)

式中:m—迭代次数。

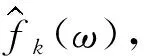
(9)

(10)

最后,通过对偶上升法,可得到拉格朗日乘数λ的简化表达式:

(11)

式中:ζ—更新参数。

VME的具体实现过程如下:

(2)令m=m+1,并执行整个循环;

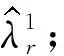
(6)设定值大于零的判别精度ξ,直到收敛满足:

(12)

收敛满足式(12)即可停止循环,输出结果;否则重新回到步骤(2)重新运算。

1.2 去趋势波动分析(DFA)

设存在时间序列x(t),t=1,2,3,…,N,对该序列进行去趋势波动分析的步骤如下:

(1)求时间序列x(t),t=1,2,3,…,N的累积离差:

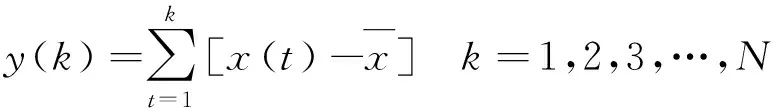
(13)

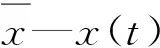
(2)将时间序列y(k)等分成Ns个不重叠的窗口,每个窗口包含s个采样点,则Ns=[N/s]。

假设每个区间都具有一个有关时间t的p阶趋势,则每个窗口内的趋势方程可表达为:

(14)

其中:通过对该窗口的数据进行最小二乘拟合,可以得到βj(j=0,1,2,…,p),则可得拟合曲线ys(k)。

(3)消除每一窗口时间序列y(k)的趋势项ys(k):

Δys(k)=y(k)-ys(k)

(15)

(4)计算时间序列Δys(k)的二阶波动函数:

(16)

(5)将窗口大小s按照一定步长递增,重复步骤(2～4),可得到波动函数F(s)随窗口大小s变化的曲线。

若该曲线服从幂律关系,则存在:

F(s)～sα⟹F(s)=Asα

(17)

上式表明,x(t)具有自相似分形特征。

分别求F(s)和s的对数,得到双对数图,则lg(F(s))与lgs呈现线性关系,其斜率便是尺度指数α,可用最小二乘法得到:

lg(F(s))=lgA+αlgs

(18)

1.3 局部保留投影(LPP)降维

令矩阵Z=(z1,z2,…,zn)∈Ra1×n为样本集合(其中:n为样本数,a1为样本原始维度),则LPP的目标函数为:

(19)

式中:a2(≪a1)—低维子空间维度。

原始空间数据投影到低维子空间中得到投影矩阵Q∈Ra1×a2。

相似性矩阵H∈Ra1×n的定义为:

(20)

式中:t—常量;τ—大于0。

经过变换与推导,LPP可定义为:

(21)

式中:L—拉普拉斯矩阵,L=G-H;G—对角矩阵。

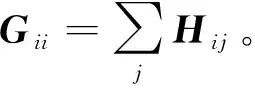
综上所述,笔者所提出方法的具体实现步骤如下:

(1)对原始液压泵振动信号x(t)进行变模式提取(VME),分解获得一系列模式分量IMFi(i=1,…,n);利用去趋势波动分析DFA的方法对分解的IMFi(i=1,…,n)计算标度指数αi(i=1,…,n);

(2)确定标度指数阈值θ,标度指数小于阈值θ对应着与噪声相关联的模式分量IMFp(p=1,…,t,t≤n),标度指数大于阈值θ对应着与噪声无关的模式分量IMFq(q=1,…,e,e≤n,n=e+t);对IMFp进行小波降噪,抑制噪声对高频有用信号的干扰;

(3)将标度指数高于阈值θ的模式分量IMFq和小波降噪后的IMFp进行信号重构,然后对重构信号计算多个统计学特征,如平均值、有效值、峰值等,利用局部保留投影算法(LPP)对高维数据进行降维,从而完成对液压泵不同故障模式的聚类分析。

笔者所提出的方法的技术路线图如图1所示。

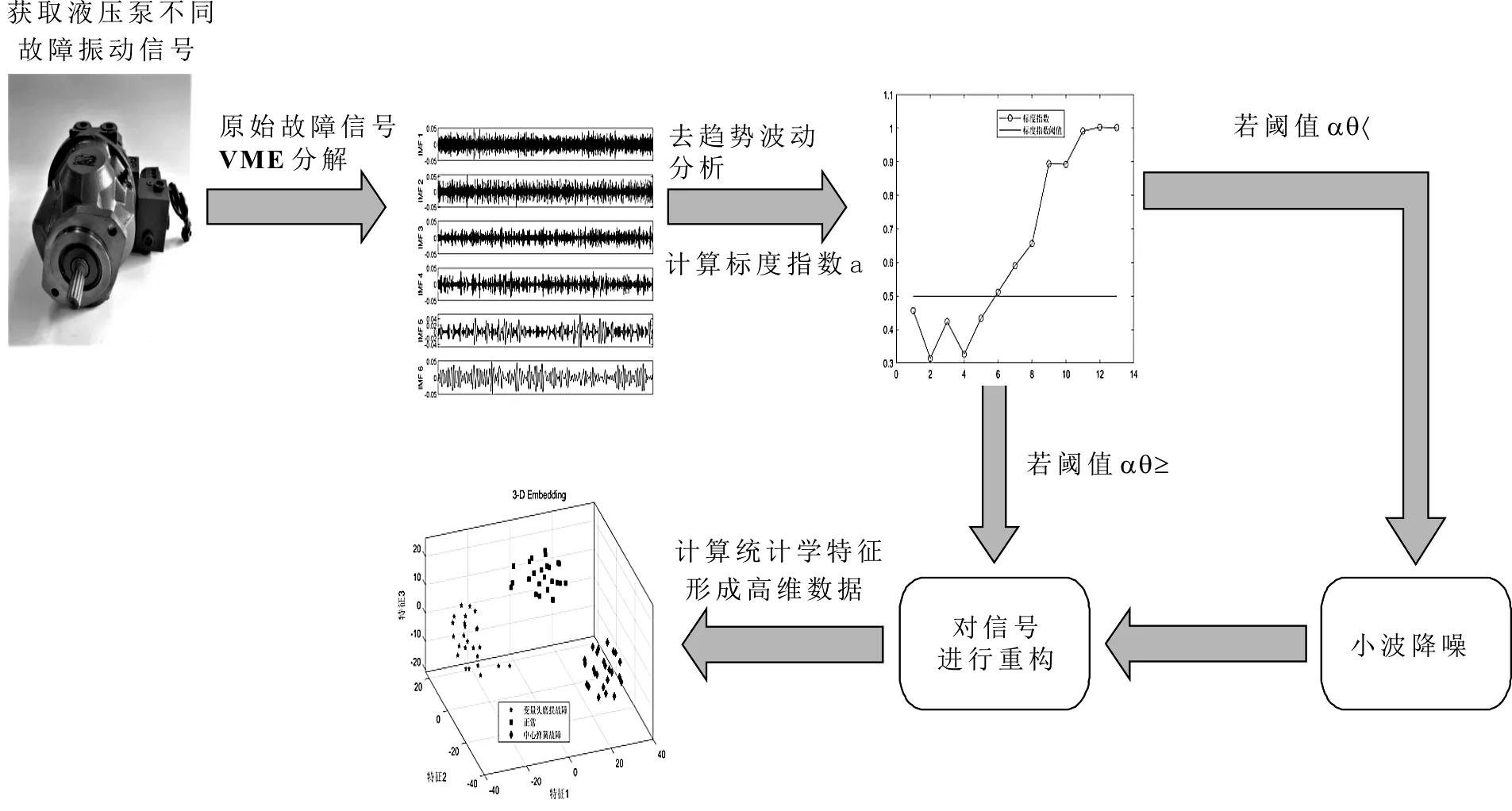
图1 该方法的技术路线图

2 液压泵故障仿真信号分析

为了说明笔者所提出方法的可行性,笔者构造仿真信号进行了验证,设置该仿真信号如下式所示:

I1(t)=3cos(60πt)
I3(t)=cos(100πt+10t)(3+sin(6πt))
I2(t)=cos(100πt+10t2)(3+cos(30πt))
I=I1+I2+I3+n(t)

(22)

式中:I—多分量调幅-调频信号,I=I1+I2+I3。

为了评价方法的噪声鲁棒性,笔者对信号添加SNR=10 dB的高斯白噪声。

仿真信号时域波形及其构成模式分量图如图2所示。

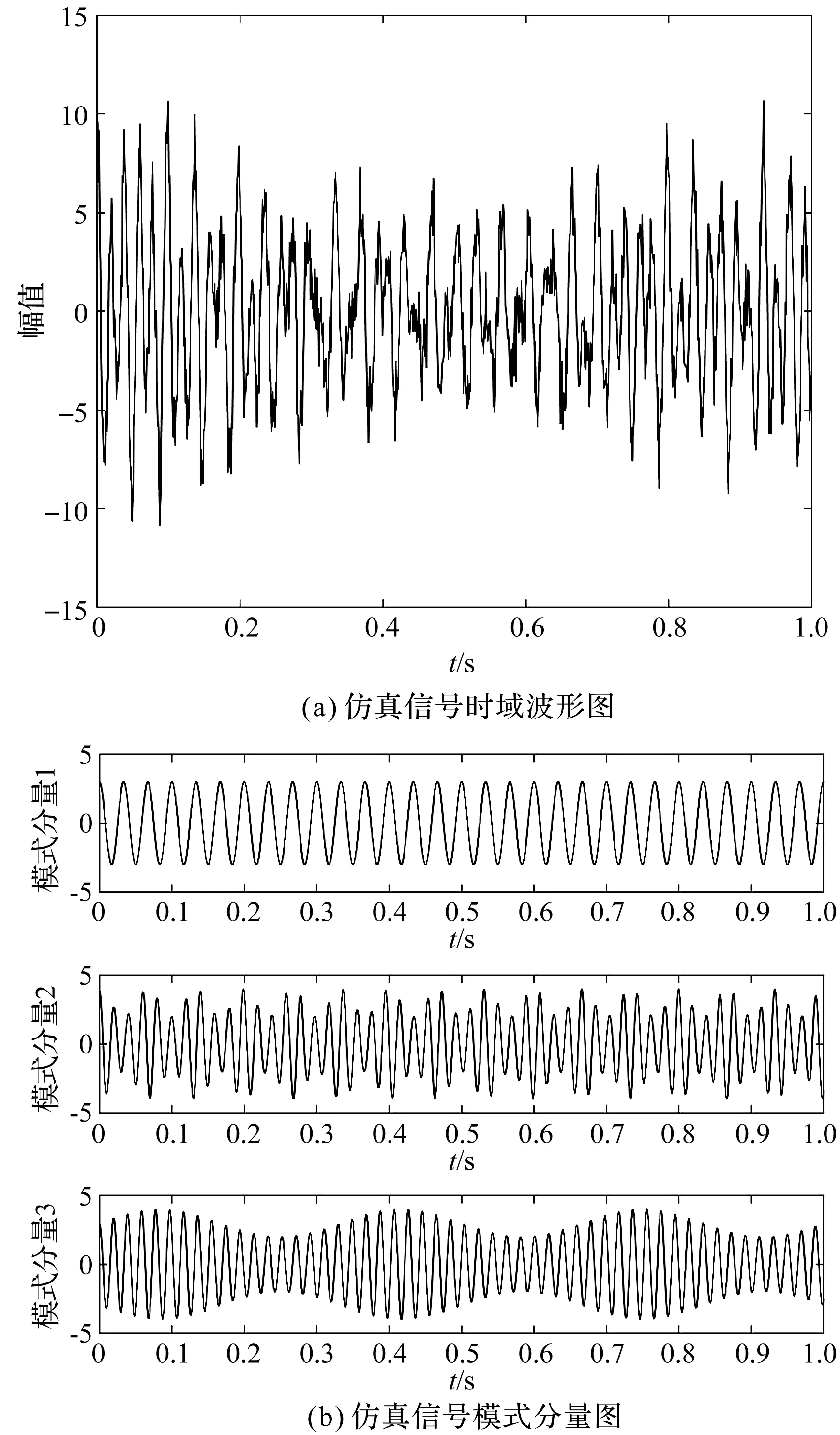
图2 仿真信号时域波形及其构成模式分量图

2.1 采用常用算法的分解结果

为了便于比较分析,笔者分别采用经验模式分解(EMD)、局部均值分解(LMD)和变分模式分解(VMD)对仿真信号进行信号分解。

采用EMD、LMD和VMD的模式分解结果如图3所示。

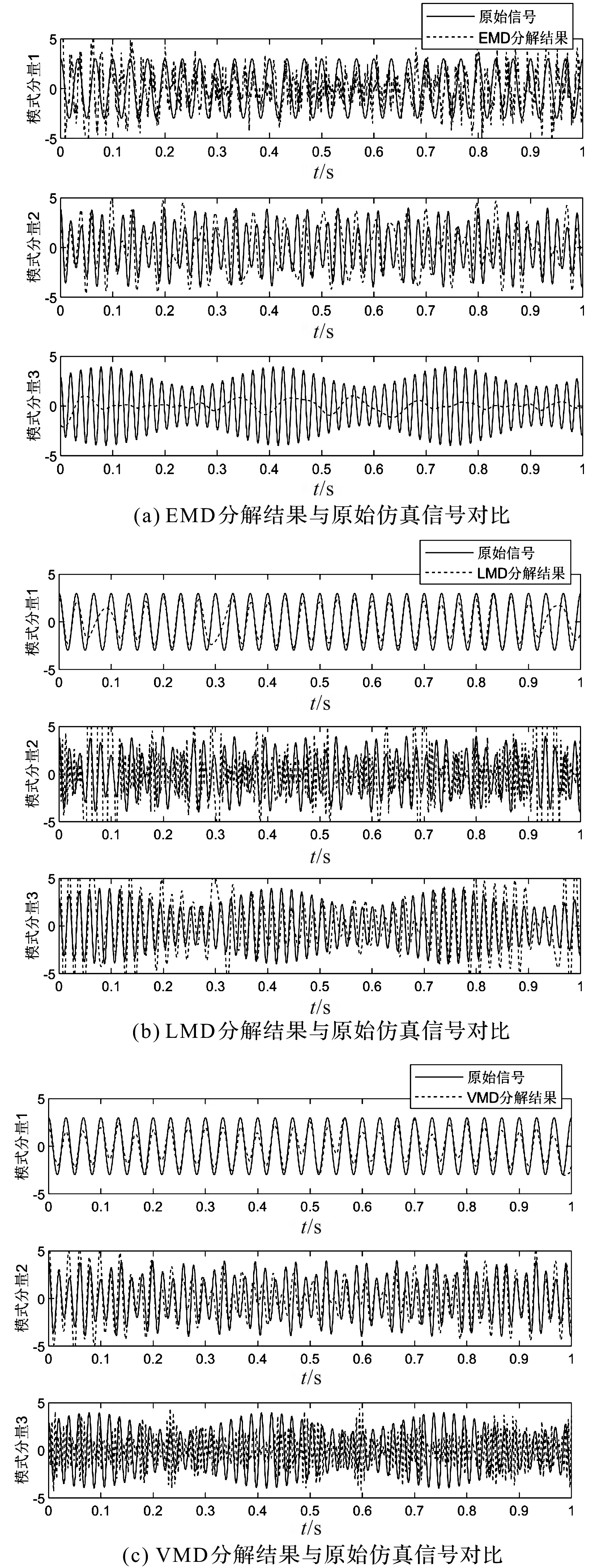
图3 EMD,LMD和VMD的模式分解结果

从图3中可以看出:由于受到噪声的影响和理论方面的欠缺,上述常用的分解算法无法将3个模式分量准确地分解出来。

为此,笔者采用VME分解算法对仿真信号进行处理。

2.2 采用VME的分解结果

VME的模式分解结果与原始信号对比如图4所示(图中,虚线分量为VME分解后的结果,实线分量为原始仿真信号)。

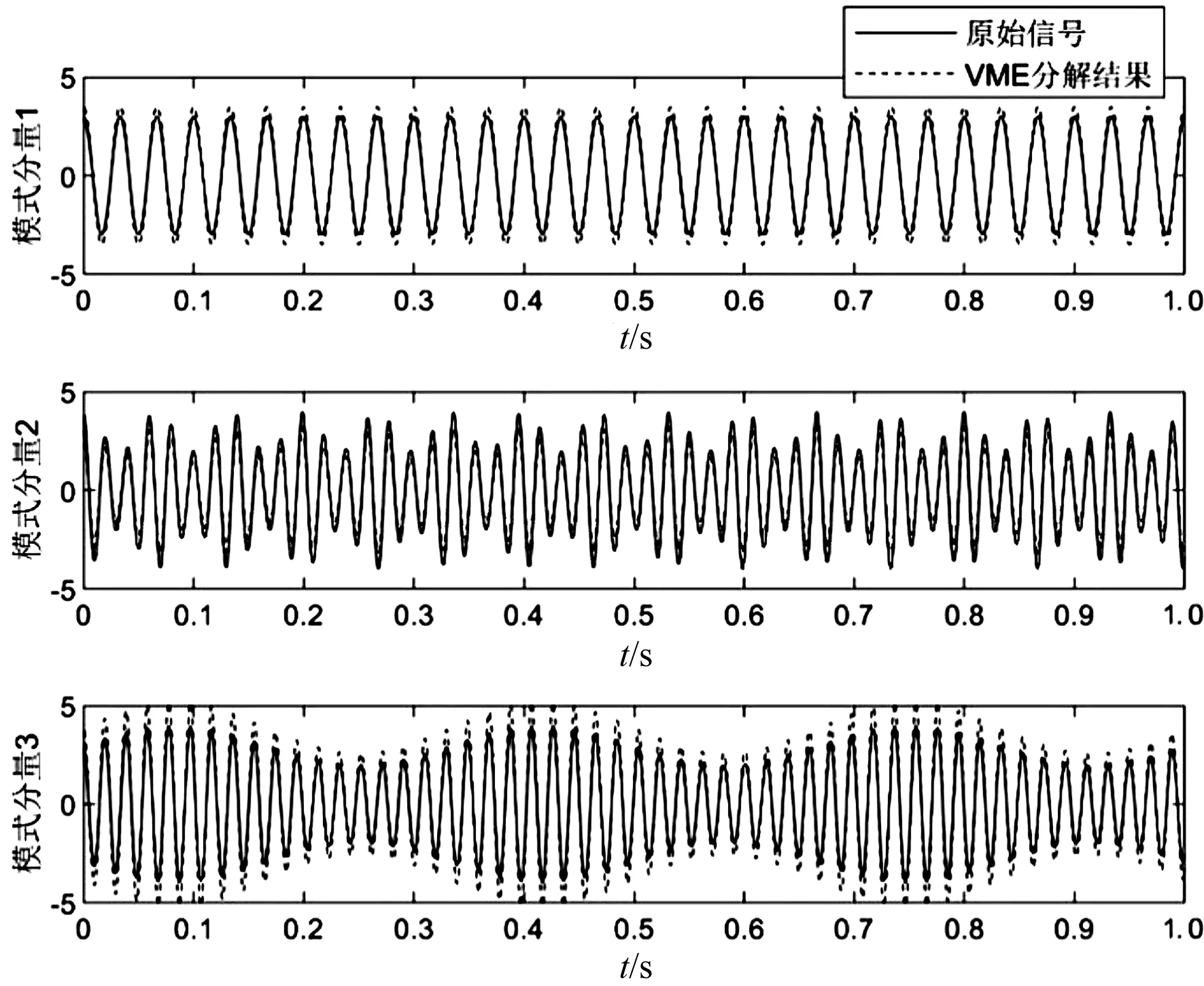
图4 VME的模式分解结果及与原始仿真信号对比

图4结果显示:VME更准确地实现了信号的模式分解,更好地保留了信号各分量的特征。

笔者根据分解结果与原始信号的偏差大小,计算各分解算法模式分解的均方根误差(RMSE)。

各算法分解结果的均方根误差如表1所示。

表1 各算法分解结果的均方根误差

通过以上比较可知:VME相较其他经典分解算法具有更好的分解效果,将其应用于液压泵振动信号分析,可以有效地实现对故障特征的识别及提取。

3 实验及结果分析

为了验证上述方法的有效性,笔者通过轴向柱塞泵液压实验系统,来对采集到的振动信号进行分析处理。

3.1 故障实验

该试验装置为斜盘式轴向柱塞泵,型号为25YCY14-1b,柱塞数为7。在实验过程中,笔者分别采集正常状态、变量头磨损故障、中心弹簧故障的泵壳振动信号,通过本文提出的方法实现液压泵3种不同故障模式的分类。

液压泵故障实验台结构简图如图5所示。

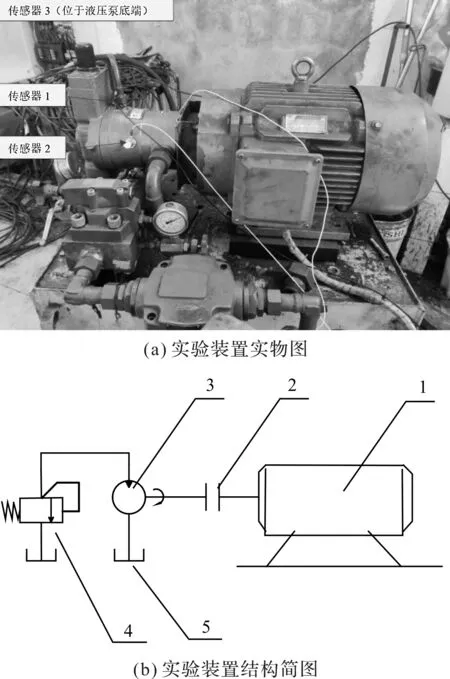
图5 液压泵故障实验台结构简图1—电机;2—联轴器;3—液压泵;4—溢流阀;5—油箱

液压泵试验参数设置表如表2所示。

表2 液压泵试验参数设置表

实验测得液压泵不同故障类型信号的时域图如图6所示。

然后,笔者对振动信号进行变模式提取(VME)分解。

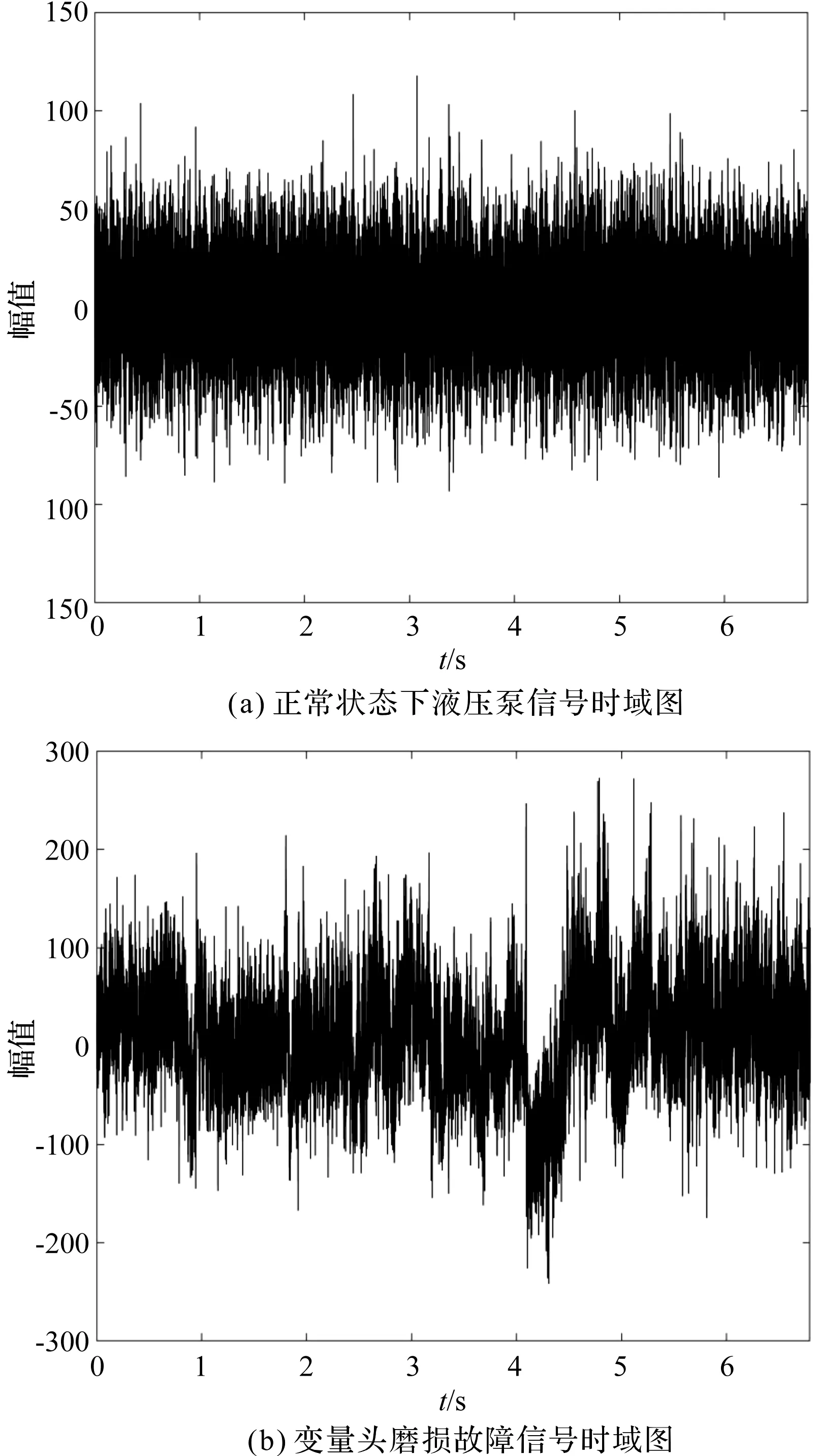
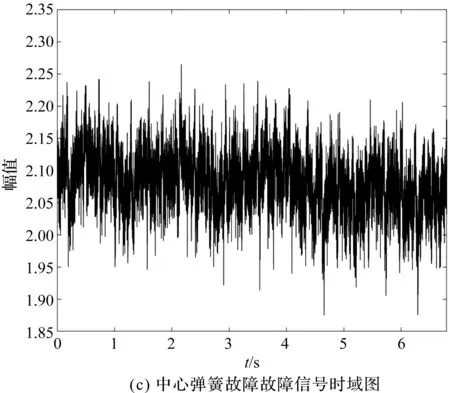
图6 液压泵不同故障类型信号时域图

液压泵不同故障类型信号VME分解示意图如图7所示。

最后,笔者利用所提出的方法,对VME分解后的信号进行去趋势波动分析,其中,标度指数的阈值设定为θ=0.5。

分解后得到的模式分量标度指数分布图如图8所示。

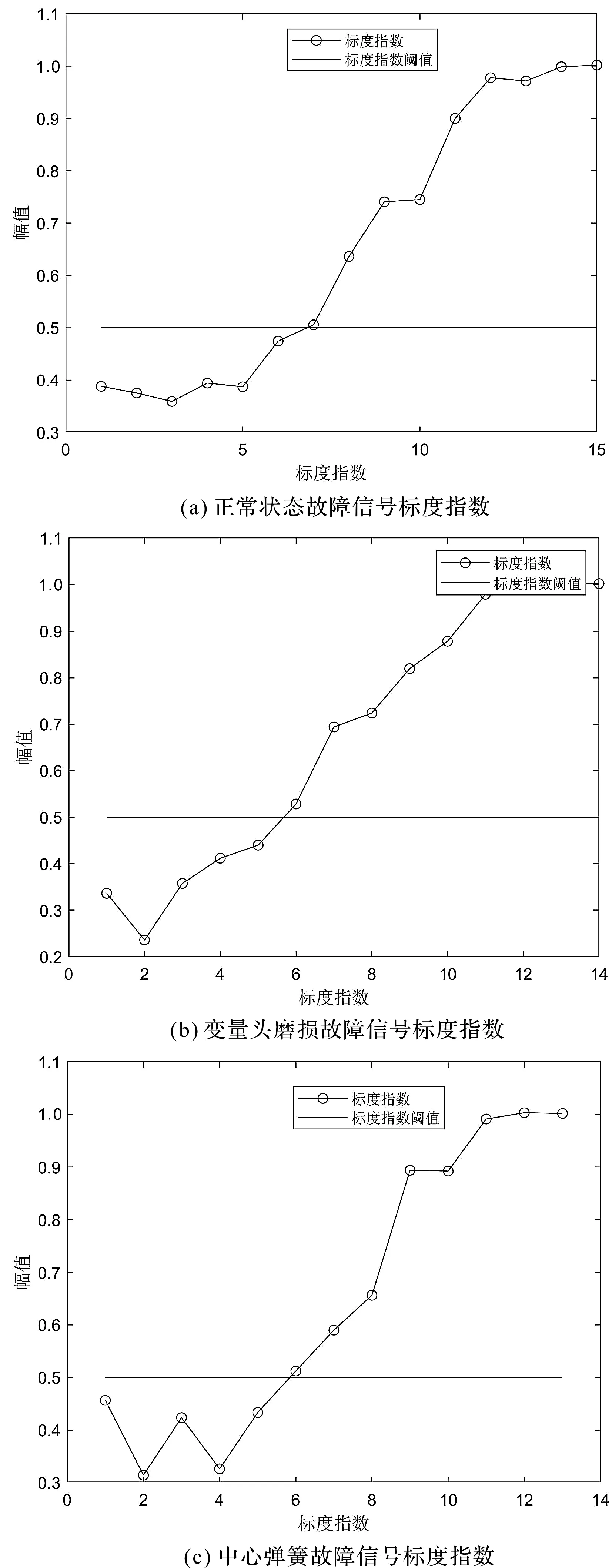
图8 分解后模式分量标度指数分布图

通过图8可以发现:前面分解得到的模式分量的标度指数都要低于阈值θ=0.5,因此,有必要对其进行降噪处理,然后进行信号的重构,以获得具有较高信噪比的液压泵振动信号。

同时,笔者通过计算平均值、有效值、峰值、方根幅值、歪度、峭度等16个重构的时域特征参数,形成高维的数据结构,并在高维空间进行LPP降维聚类。

采用笔者提出的方法对液压泵故障进行分类识别,所得的结果如图9所示。

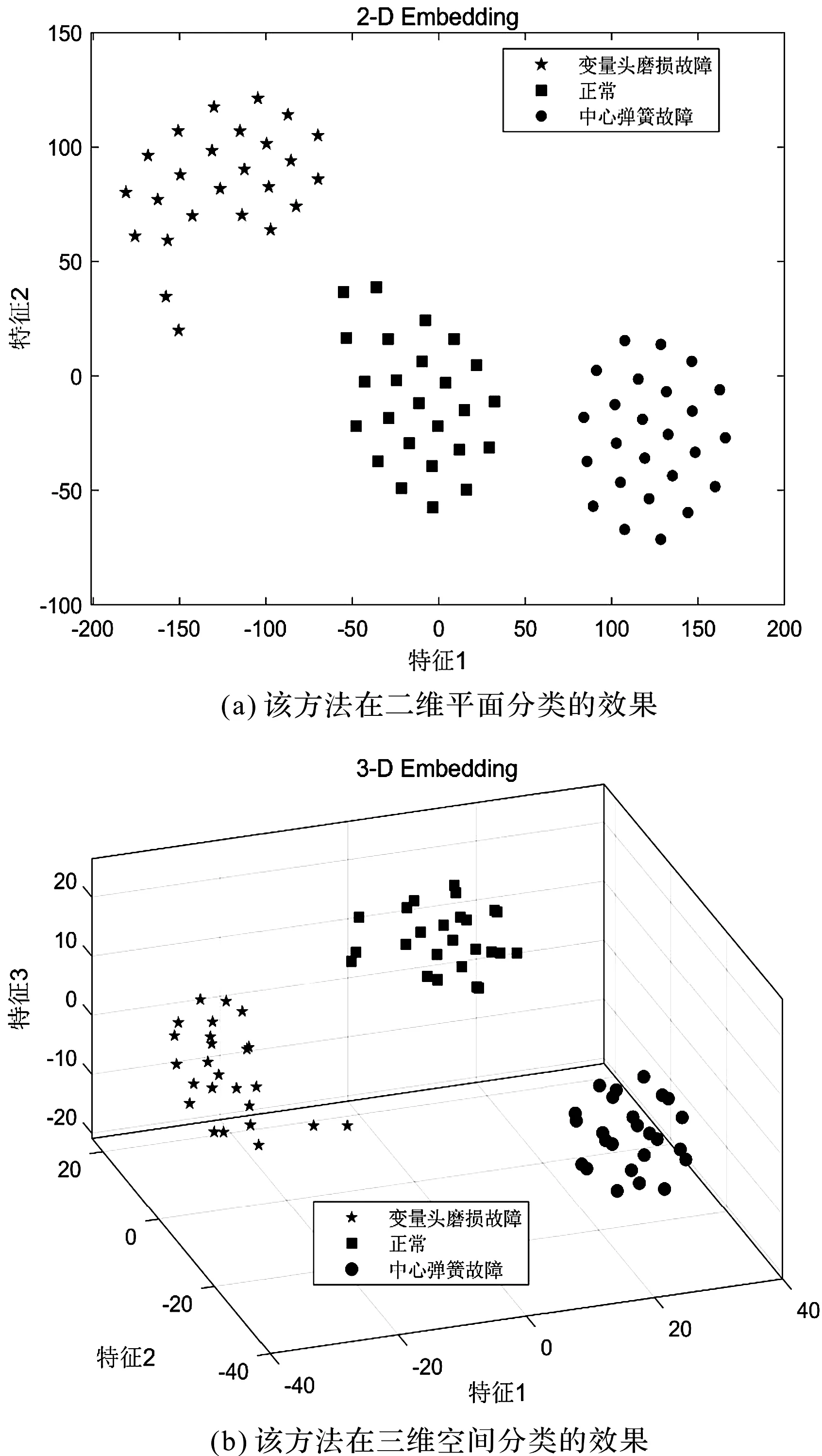
图9 该方法对液压泵故障分类的结果

3.2 对比分析

为了进一步说明该方法的有效性,笔者不用变模式提取(VME)方法和去趋势波动分析(DFA)的手段进行信号的分解和重构,而直接利用经典的PCA及LPP算法对原始数据进行多统计学特征计算,并进行降维聚类。

笔者采用其他降维方法对液压泵故障进行分类识别,所得的结果如图10所示。

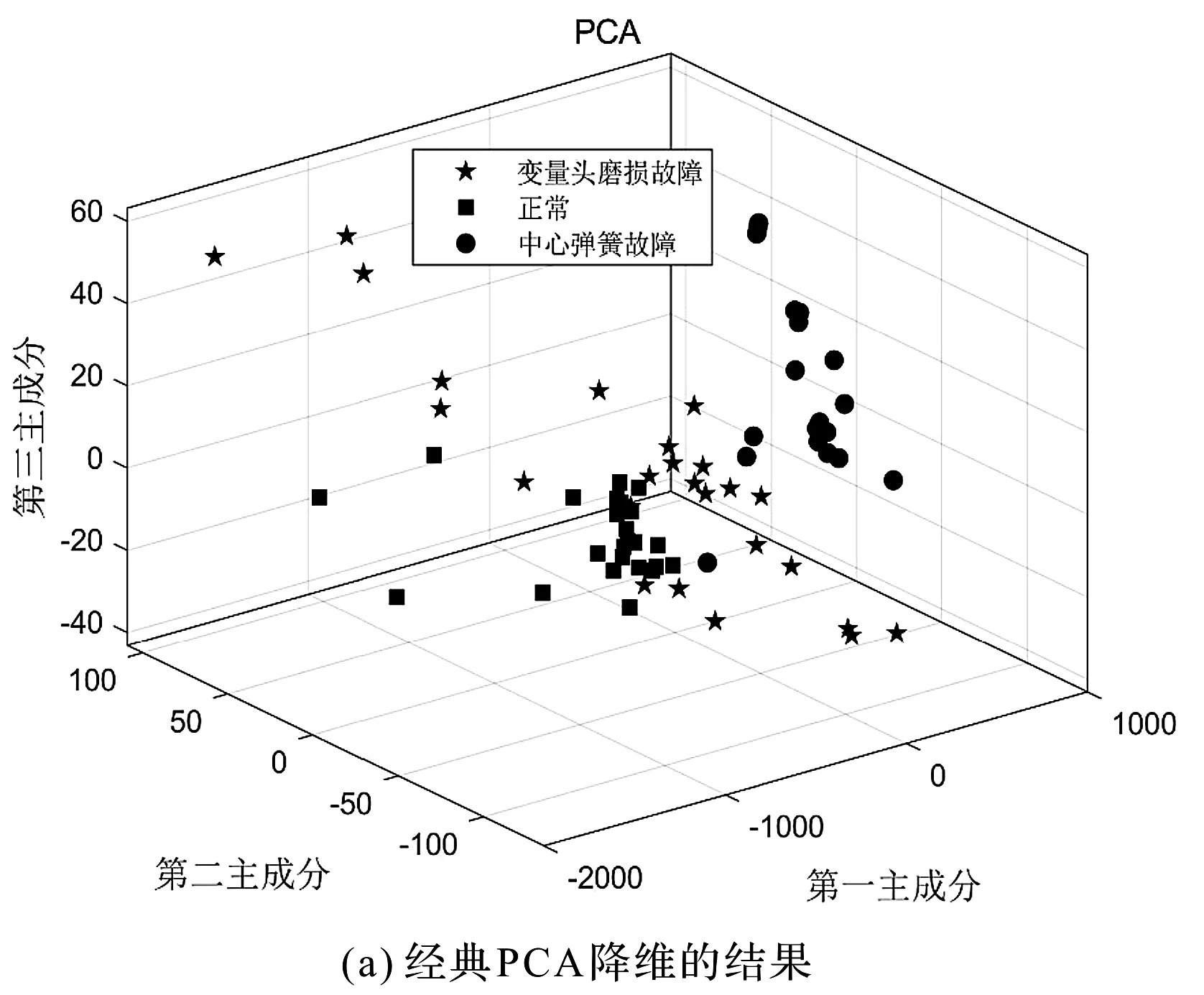
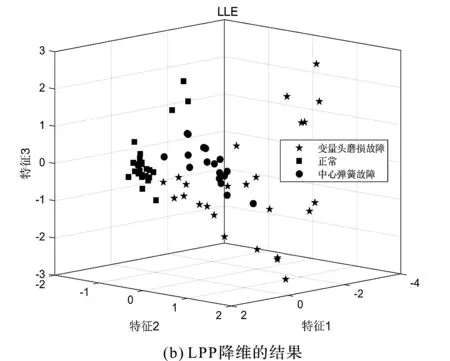
图10 其他降维方法对液压泵故障分类的结果

通过对比图9与图10可以看出:笔者提出的联合VME方法和DFA的方法,在液压泵故障信号降噪和降维处理上具有更佳效果,能够对多个不同故障类型的振动信号进行准确识别。

4 结束语

为了解决液压泵故障诊断识别精度不高的问题,笔者提出了一种基于变模式提取(VME)与去趋势波动分析(DFA)的信号去噪方法,并利用局部保留投影(LPP),实现了对液压泵不同故障类型的准确聚类。

该研究的主要内容和结论如下:

(1)利用变分模式提取(VME)的方法对液压泵振动信号进行了模式分解,消除了分解过程中对分量数量的限制,提高了其运算效率;

(2)通过去趋势波动分析(DFA)方法,对提取的模式分量计算相应的标度指数,利用标度指数作标准来判断是否运用小波降噪进行处理,并通过LPP算法对数据进行了降维和聚类分析;

(3)将笔者所提方法应用于液压泵故障实验台振动信号分析,结果表明,该方法可以作为机电系统液压故障诊断的一种手段。

在后续的研究中,笔者将针对二元甚至多元的VME,推导出多元变分模式提取算法,并将其应用于机电系统故障诊断中。