基于AMESim-MATLAB的伺服直驱闭式泵控系统仿真模型*

张敬芳,陈文斌,仇庚廷,杨明昆,陈革新*,艾 超

(1.河北机电职业技术学院 机械工程系,河北 邢台 054000;2.燕山大学 机械工程学院,河北 秦皇岛 066004;3.燕山大学 河北省重型机械流体动力传输与控制实验室,河北 秦皇岛 066004;4.燕山大学 先进锻压成型技术与科学教育部重点实验室,河北 秦皇岛 066004)

0 引 言

在电液伺服控制系统中,虽然伺服阀控系统具有良好的控制性能[1-3],但因其系统构型复杂,溢流与节流的损失会使系统严重发热,导致系统功率损失很大[4,5]。

伺服直驱闭式泵控系统主要是通过伺服电机的旋转,来同轴驱动液压泵,从而起到调节系统的输出压力与流量,改变液压执行机构运动的目的[6]。该系统具有高效节能、功重比大、环境友好、对油品要求低等优点[7],发展应用前景广阔。

由于伺服直驱泵控系统是典型的机电液系统,存在负载参数时变、外部激励与内部干扰严重、机电液多参量作用等问题,尤其是在伺服直驱泵控系统的位置控制方面。

FU Yong-ling等人[8]设计了一种非线性比例积分位置控制器,用该控制器来补偿静摩擦带来的不利影响,使得伺服直驱泵控系统具有了较高的位置精度。喜冠男等人[9]采用分段PID控制、速度分级控制和复合控制方法,来对位置进行控制,有效提高了泵控系统的响应速度和位置精度。CAO Fu-lu等人[10]应用遗传算法对PID控制器的参数进行了优化,提高了系统的响应速度,降低了系统的稳态误差。陈革新等人[11]提出了一种电液伺服闭式泵控系统的位置前馈补偿控制算法,采用该算法可以大幅提高系统位置的控制性能。王玄等人[12]设计了一种基于预测控制的模型预测控制器,有效解决了泵控非对称液压缸系统位置的超调问题。ZAD H等人[13]设计了一种预测控制器,增强了系统位置控制的抗扰动能力,提高了系统的鲁棒性。魏晓朝等人[14]采用了遗传算法来优化前馈-反馈PID控制,以减少系统的超调量与调节时间,增强了系统的控制性能[15，16]。REZAYI S等人[17]提出了一种新型滑模变结构控制策略,解决了具有加速度约束的电液伺服系统的位置跟踪问题。REN Guangan等人[18]基于定量反馈理论设计了一种线性位置控制器,增强了系统位置控制的抗摄动能力。

上述研究多从控制策略层面提高了系统位置的控制精度,增强了系统鲁棒性,但并没有从仿真模拟的角度对系统进行分析,并且没有搭建相应的仿真模拟数字平台。

针对上述缺陷,笔者以位置控制为目的,利用AMESim与MATLAB来仿真模拟系统的运行状态,并根据现有实验条件,对仿真模型的仿真效果进行验证。

1 伺服直驱闭式泵控系统

1.1 系统原理介绍

笔者建立了伺服直驱闭式泵控系统,该系统的液压原理图如图1所示。

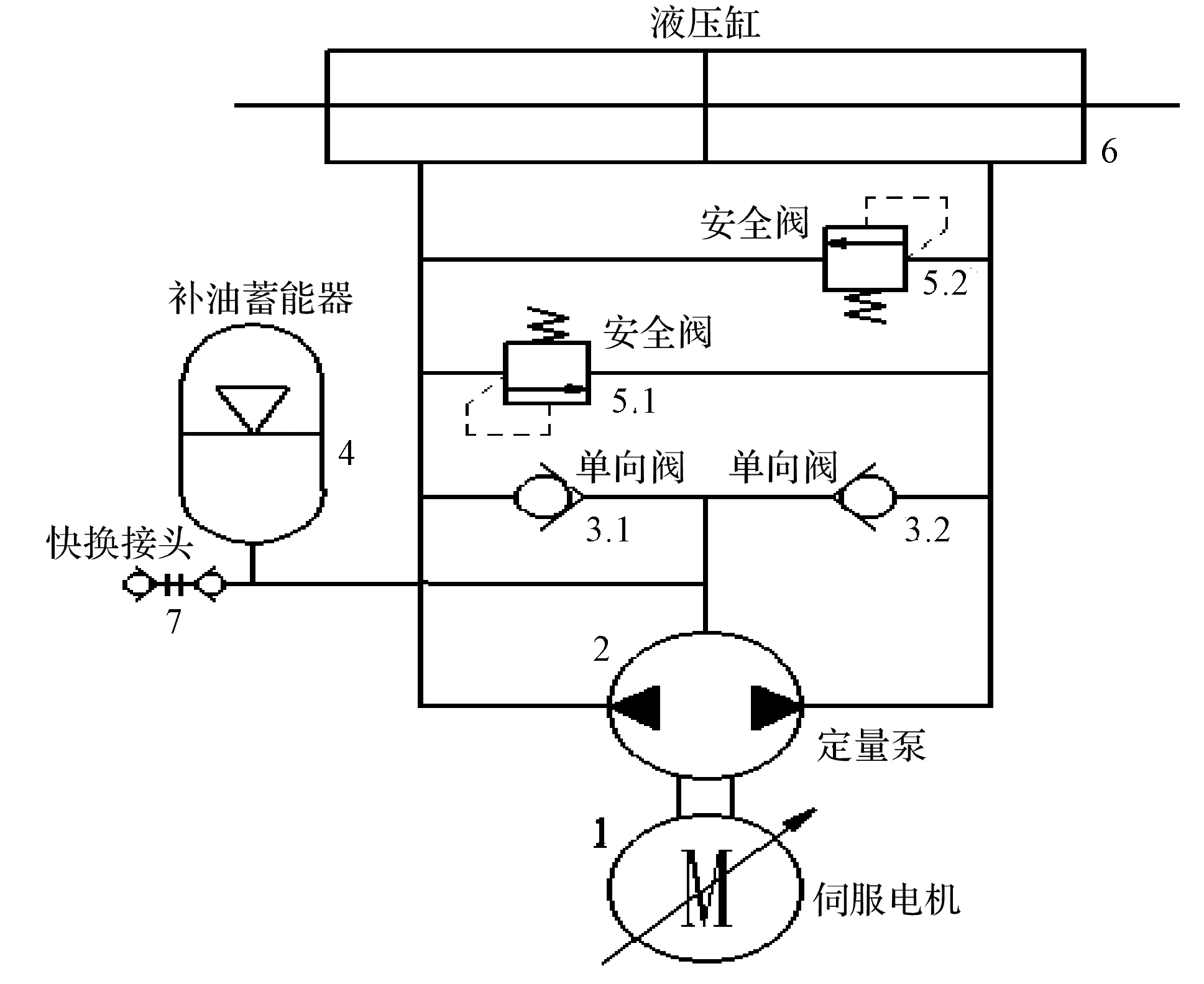
图1 伺服直驱闭式泵控系统液压原理图

图1中,安全阀在系统中起安全保护作用,定量泵两端直接与两活塞杆腔相连;伺服电机通过改变转速与转矩,对系统的流量和压力进行控制,从而可以调节液压缸作用在负载上的位移与出力。

当系统油液泄漏时,可采用蓄能器起补充作用,避免电机出现吸空现象;当系统中油液压力低于设定值时,可外接泵站,经由快换接头对系统油液进行补充。

安全阀对液压缸左右两腔极限压力值起限制作用。当压力升高时,多余油液进入补油蓄能器中。

1.2 数学模型建立

(1)伺服电机数学模型

首先,笔者建立了伺服电机的数学模型。其中的定子磁链方程为:

(1)

式中:ψdψq—定子磁链d-q轴分量;LdLq—定子电感d-q轴等效电感,H;idiq—定子电流d-q轴分量,A;ψf—永磁体磁链,H。

定子电压方程为:

(2)

式中:UdUq—定子电压d-q轴分量,V;Rs—定子电阻,Ω;ωe—转子角速度,rad/s。

电磁转矩方程为:

(3)

式中:Te—电磁转矩,N·m;Pn—极对数。

运动方程为:

(4)

式中:TL—电机轴负载转矩,N·m;JL—等效转动惯量;ωm—电机机械角速度,rad/s;D—电机阻尼系数。

负载扭矩方程为:

(5)

式中:V—液压泵排量,L/min;ΔP—液压泵进出口压差,bar;ηm—液压泵容积效率;K—比例系数。

(2)定量泵数学模型

然后,笔者建立了定量泵的数学模型,其方程式为:

Qp=Dpωp-CpPL

(6)

式中:Qp—定量泵输出流量,m3;Dp—定量泵额定排量,m3/rad;ωp—定量泵角速度,rad/s;Cp—定量泵泄漏系数,m3/(s·Pa);PL—系统压力,MPa。

(3)液压缸数学模型

最后,笔者建立了液压缸的数学模型。其液压缸的流量连续性方程为:

(7)

式中:QL—液压缸负载流量,m3;Ap—液压缸有效作用面积,m2;xp—液压缸输出位移,m;Ctc—液压缸总泄漏系数,m3/(s·Pa);Vt—总压缩容积,m3;βe—有效体积弹性模量,Pa。

液压缸和负载力平衡方程为:

(8)

式中:mt—活塞上总质量,kg;Bp—总粘性阻尼系数,N/(m·s-1);K—负载弹簧刚度,N/m;FL—活塞上的任意外负载力,N。

2 AMESim与MATLAB联合仿真

2.1 系统AMESim模型

笔者建立伺服直驱闭式泵控系统的AMESim模型,如图2所示。

图2 伺服直驱闭式泵控系统AMESim模型1—伺服电机;2—转换增益;3—控制模块;4—定量泵;5—液压油;6—蓄能器;7—补油单向阀;8—安全溢流阀;9—干扰信号;10—干扰力;11—位移传感器;12—外负载;13—液压缸

图2中,除液压基本元件外,系统AMESim模型中还包括位移传感器、外负载模块、干扰信号模块等。

AMEsim模型参数如表1所示。

表1 AMEsim模型参数表

2.2 控制器设计

在滑模运动中,要先有一个向滑模面靠近的过程,该过程考验的是系统能否快速响应;然后,要确保对象在滑模面上能稳定、准确地运行。

为了提高系统的快速性与稳定性,第一阶段要基于指数趋近律的控制策略,引入等效控制部分,以便控制对象快速达到滑模面,缩短系统的响应时间;第二阶段要利用模糊控制理论,解决控制的切换问题,以基本消除系统抖振现象,使系统整体性能得到显著提高。

最终,笔者以普通滑模运动为基础,建立了改进控制算法,并利用MATLAB的Simulink模块建立了控制器模型,如图3所示。

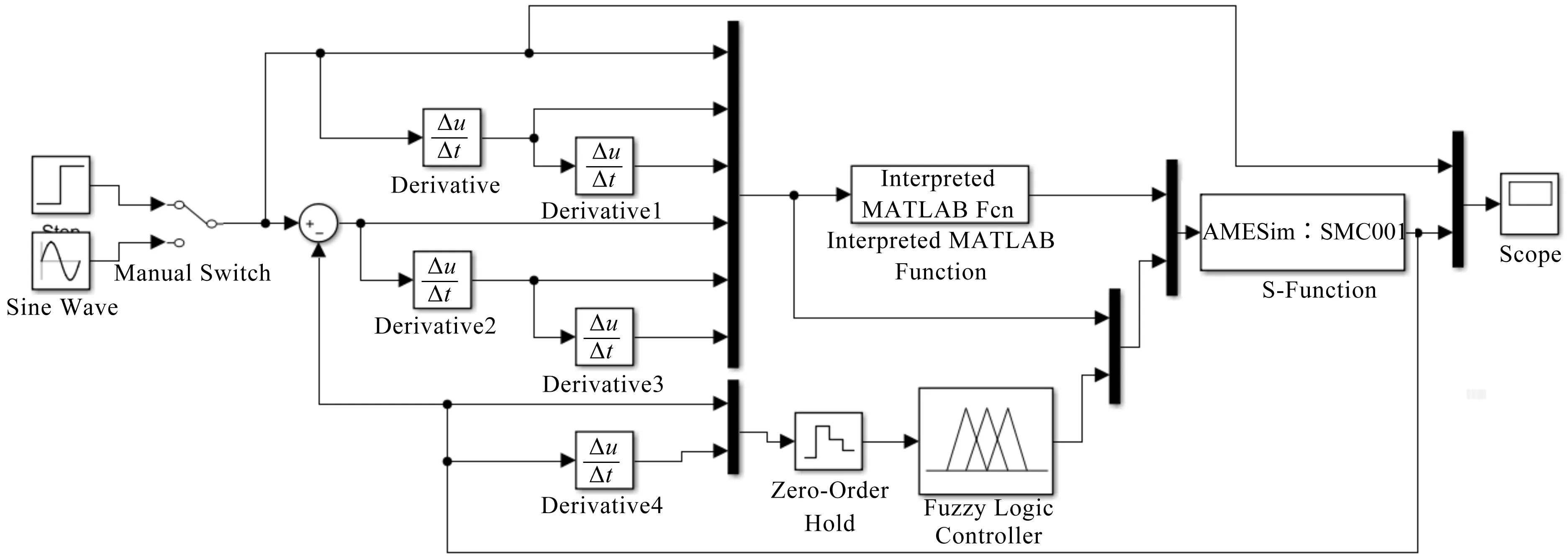
图3 数学模型仿真图

2.3 系统联合仿真

笔者按以下步骤建立其数字模拟平台:

(1)为保证模型间的实时沟通,需正确安装系统编译器;

(2)对两模型间的沟通变量进行设置;

(3)设置两模型间的接口路径。其中,关键一步是解决AMESim与Simulink的接口路径设置问题,保证MATLAB能够在AMESim中顺利启动。

此处将两平台通讯类型设置为SimuCosim通讯。同时,为方便仿真设计,要引出AMESim仿真模型中系统的位移信号和控制信号。

Simulink与AMESim的接口设置图如图4所示。

图4 Simulink与AMESim的接口设置图

3 实验及结果分析

3.1 实验平台

该实验平台由液压部分与电气部分两部分组成。其中,液压部分由蓄能器、内置式位移传感器等基本元件组成,如图5所示。

图5 液压实验平台

除断路器、继电器等基本元件外,实验平台的电气部分还包括制动电阻、倍福采集模块、电抗器、穆格二代控制器、驱动器等元件,如图6所示。

图6 电气柜图

笔者利用穆格控制器软件MACS,基于Codesys编程语言,编写了改进滑模变结构控制算法的程序,经编译成功后进入实验流程。

系统模拟量与数字量由倍福采集模块传输至控制器中进行处理,控制器经一定运算处理后,反馈到电机电流环中进行控制。

3.2 实验结果分析

3.2.1 阶跃响应关键参数曲线分析

当系统的输入信号为阶跃信号时,笔者将液压缸位移的期望位置、实验平台实际位置、理论平台仿真位置三者进行了对比。

其中,位移曲线对比图如图7所示。

图7 位移曲线对比图

由图7可知:(1)该仿真平台得到的结果基本上与阶跃输入信号及实验结果相吻合;(2)系统的稳态精度较高。

3.2.2 正弦响应关键参数曲线分析

当系统的输入信号为频率0.5 Hz,振幅20 mm的正弦信号时,仿真模型与实验平台的液压缸位移响应曲线的对比结果,如图8所示。

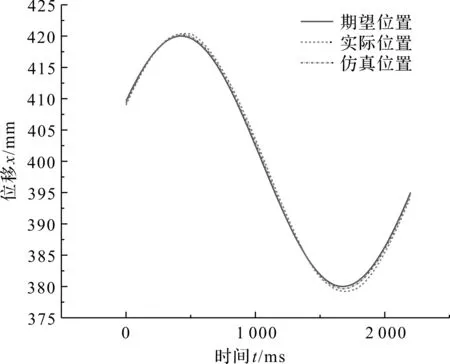
图8 位移曲线对比图

由图8可知:(1)仿真平台对正弦输入信号的响应较为理想,与实验结果较为吻合;(2)实验结果仍存在一定的超调与滞后现象,需要对系统部分参数做进一步的整定。

4 结束语

为了实现伺服直驱闭式泵控系统对位置的高精度控制,笔者提出了一种基于AMESim与MATLAB的伺服直驱闭式泵控系统仿真模拟平台。

首先笔者建立了伺服电机、液压泵、伺服缸数学模型,然后建立了整个液压系统的仿真模型,并基于MATLAB建立了改进滑模变结构控制策略的数学模型,最后将正弦与阶跃位置输入信号下实验平台与仿真模型得到的结果进行了对比分析,结果表明,该仿真平台在允许误差范围内基本与实验曲线相吻合,该仿真模型能够反映系统的动态响应特性。

具体的过程主要有:

(1)在AMESim-MATLAB软件中构建了系统数学模型,并对接口参数进行了配置;

(2)将正弦信号与阶跃信号作为输入信号,对比分析了实验平台与仿真模型得到的结果,得到了系统的跟随性能与稳态精度;

(3)实验结果表明:在阶跃位置输入信号下,系统响应时间约为2 s,稳态精度达0.01 mm;在正弦位置输入信号下,系统幅值约有0.25 mm误差,相位滞后约10°,在允许的误差范围内。

在后续的研究中,笔者将基于该伺服直驱闭式泵控系统仿真模型,进行高性能控制算法的实践。