基于随机森林的滚动轴承故障辨识方法研究*

王兰兰,朱 捷,周正平,常兆庆

(1.郑州铁路职业技术学院,河南 郑州 451460;2.郑州航空工业管理学院 管理工程学院,河南 郑州 450046;3.南京航空航天大学 自动化学院,江苏 南京 211106;4.江苏曙光光电有限公司,江苏 扬州 225000)

0 引 言

滚动轴承是旋转机械的关键部件,一旦其发生故障,会严重影响设备的安全稳定运行,并可能会造成安全事故,以及难以估计的经济损失。因此,准确识别滚动轴承的故障状态,并对轴承进行故障诊断具有重要的意义[1,2]。

滚动轴承故障辨识属于典型的多分类问题。随着当前机械设备(旋转机械)逐步向大型化和系统化方向发展,轴承的故障特征也往往具有多样性;并且在对轴承的故障进行信息处理过程中,还往往存在进化的知识,因此,在处理这类复杂数据时,采用传统的单一分类器往往会显得力不从心。

为了提高最终的故障辨识效率,利用融合算法整合多个分类器,将是今后轴承故障辨识领域研究的关键之一[3,4]。

随机森林(random forests,RF)是集成学习的代表算法之一。该算法通过将随机性引入到决策树中,改善了决策树易过拟合的现象,解决了人工神经网络(artificial neural networks,ANN)收敛速度过慢,且易陷于过拟合的问题;同时,也克服了支持向量机(support vector machines,SVM)在处理大样本数据时能力不足的缺点。随机森林算法具有较强的抵抗噪声干扰能力,通过集成多种特征向量,可以有效地提高故障诊断的准确率。

吴海滨等人[5]通过改进多尺度幅值感知排列熵与随机森林,解决了滚动轴承故障类别辨识问题,以及对故障严重程度进行分类的问题。张西宁等人[6]提出了一种基于多维缩放和随机森林的轴承故障诊断方法;该方法先利用多维缩放对故障特征集进行了降维处理,再利用随机森林算法对轴承故障进行了辨识。

为了解决传统的随机森林算法存在的故障特征数目过大、复杂度过高及易产生过拟合等问题,李兵等人[7]提出了一种基于改进随机森林的故障诊断方法;该方法分别改进了决策树bagging方式和综合投票方法,可以很好地对电机轴承故障状态进行识别。者娜等人[8]先利用变分模态分解(VMD)方法,对轴承故障原始信号进行了预处理,并提取出了其特征向量,然后利用随机森林模型对反应堆金属撞击信号进行了识别。陈石等人[9]提出了一种基于小波包能量熵和随机森林的级联H桥多电平逆变器故障诊断方法;该方法利用PCA对故障特征进行了降维,然后再利用随机森林算法对逆变器故障进行了分类,提高了逆变器故障识别的准确率。

由此可见,随机森林算法目前已广泛应用于故障诊断、数据挖掘和图像处理等领域[10-12]。

基于上述分析,笔者提出一种基于随机森林的滚动轴承故障模式辨识方法。首先,提取出滚动轴承振动信号的时域统计指标,作为特征向量;然后,利用随机森林算法对滚动轴承故障进行诊断;最后,利用综合故障模拟实验台的轴承数据,将其与传统分类器的诊断结果进行对比,以验证该模式辨识方法的有效性。

1 原理介绍

随机森林(RF)[13,14]是以CART决策树作为弱分类器的一种集成学习算法。该算法在决策树的基础上引入随机属性选择,其本质是一个包含多个决策树的组合分类器,由Leo Breiman和Adele Cutler于2001年提出。

随机森林由多个决策树{h(x,θm),m=1,2,…M}组成,其中,θm是相互独立的随机向量,其最终的分类结果由多个决策树的综合投票来决定。相比于单个分类器,随机森林算法具有更好的分类结果,可以有效地提升学习系统的泛化能力。

假定一数据集为D={Xi,Yi},Xi∈Rk,Yi∈{1,2,…c},随机地建立一个由多个决策树{h(x,θm),m=1,2,…M}组成的森林,各决策树之间没有关联,当输入样本xi时,随机森林的基决策树都会给出各自的识别结果,最后将投票数多的类别作为该输入的最终分类。

随机森林算法流程如下:

(1)利用bootstrap重采样方法[15]从原始数据集中随机抽取n个样本,组成单决策树的训练集(依次为每一个bootstrap训练集训练组建分类数,共产生n棵决策树构成一片“森林”,这些决策树均不进行剪枝),每个训练集大小约为原始数据集的2/3。虽然随机的有放回采样存在一定的重复率,但可以避免决策树陷入局部最优的情况;

(2)定义训练样本的输入特征个数为M。随机森林中的单棵决策树从根节点开始自上而下递归分裂,每棵决策树在每个节点上分裂时,从M个特征向量里随机(无放回)选择m个特征向量(m取M的向下整数),然后按照分裂节点不纯度最小的原则从上述特征中挑选出一个最好的特征进行分裂生长。m在整个森林生长的过程中保持不变,重复上述过程依次分裂,直至该决策树遍历所有的特征属性;

(3)在分类阶段,通过集合n棵决策树的分类结果,采用相对多数投票原则来决定样本的类别。

随机森林的分类原理决定了它在处理数据时,能够避免由于模型输入数据维数上升而使得分类精度下降的情况,保证了在原始信号特征维数较大的情况下,仍能获得良好的分类效果。

随机森林分类过程如图1所示。

图1 随机森林分类过程

2 随机森林分类模型

2.1 振动信号采集

此处的原始数据来源于一双跨双转子综合故障模拟平台—HZXT-DS-001型综合故障模拟实验台。

该综合故障模拟平台实物图如图2所示。

图2 双跨双转子综合故障模拟平台

该综合故障模拟平台的轴承安装端实物图,如图3所示。

图3 故障轴承安装端

由图3左半部分可见,采样通道共5个。

实验中,笔者测得滚动轴承NSK6308在滚动体故障、保持架故障、内圈故障、外圈故障、正常情况共5种状态下的振动信号各80组。其中,训练样本30组,测试样本20组,剩下30组作为验证样本。

采样转速分别为2 600 r/min、2 800 r/min、3 000 r/min、3 200 r/min,采样频率为8 kHz。

2.2 振动信号处理及特征提取

采样转速在3 000 r/min下,在通道1中采集到滚动轴承的5种运行状态结果,如图4所示。

图4 滚动轴承在部分故障下的振动信号

为了降低采集到的原始信号中环境噪声等干扰信息,笔者先将原始振动信号经一维小波消噪,然后再提取信号中所包含的时域、频域和时频域的多域特征。

最后笔者提取到的16个多域特征如表1所示。

由于有5个通道,此处共可得到5×16=80维的特征,笔者将原始的特征数据集归一化处理至[-1,1]的区间。

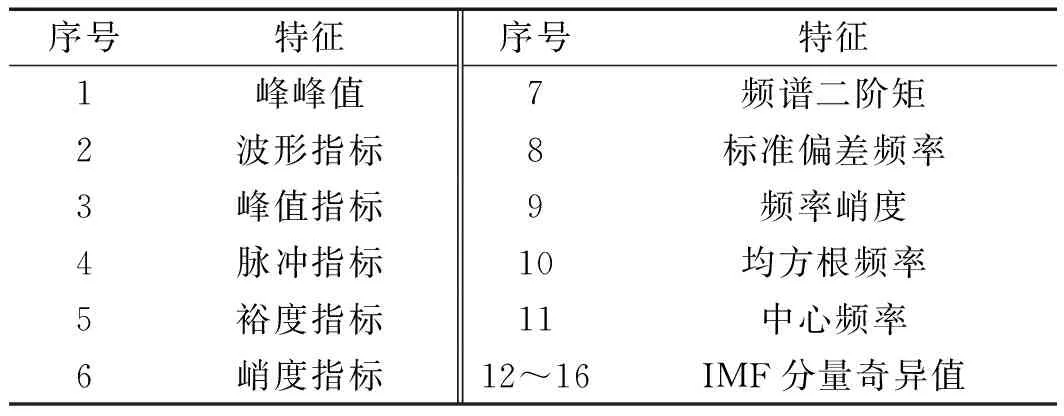
表1 为chi通道构造的原始特征参数(i=1,2,3,4,5)

2.3 基于随机森林的故障辨识模型建立

基于随机森林算法的故障辨识具体流程如下:

输入:高维特征训练集T和测试集U;

输出:故障类别集S;

(1)采集振动数据,并进行处理;

(2)从时域、频域和时频域方面提取特征指标,构建原始数据特征集并进行数据归一化处理;

(3)随机森林故障辨识

1)Fori=1 ∶N(i为基学习器数目,此处的基学习器为决策树)

①对训练集T采用Bagging方法中的重采样算法,得到训练子集Ti;

②利用训练子集Ti训练出决策树,为Hi;

③将测试集U输入至Hi,得到结果Si;

2)对Si利用相对多数投票法得到最终分类结果S;

End

随机森林中基决策树数目与辨识精度的关系曲线图如图5所示。

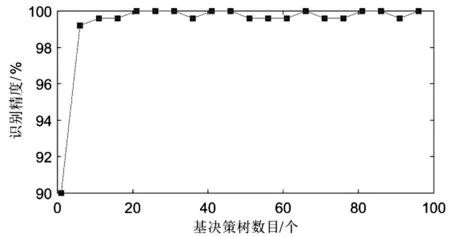
图5 随机森林中基决策树数目与辨识精度的关系

从图5中可以看出:随着基决策树数目增多,随机森林的分类准确率逐渐增加。

图5中,由于基决策树数目为30,笔者在保证单个决策树的识别精度不低于65的基础上,将每个输入值各决策树的特征数设为35。

3 实验与结果分析

3.1 不同转速下随机森林法辨识结果

为了对随机森林故障辨识模型的故障分类能力进行验证,在2 600 r/min、2 800 r/min、3 000 r/min、3 200 r/min几种采样转速下,笔者分别对几种故障状态进行故障辨识。

不同转速下,随机森林的分类识别率如表2所示。

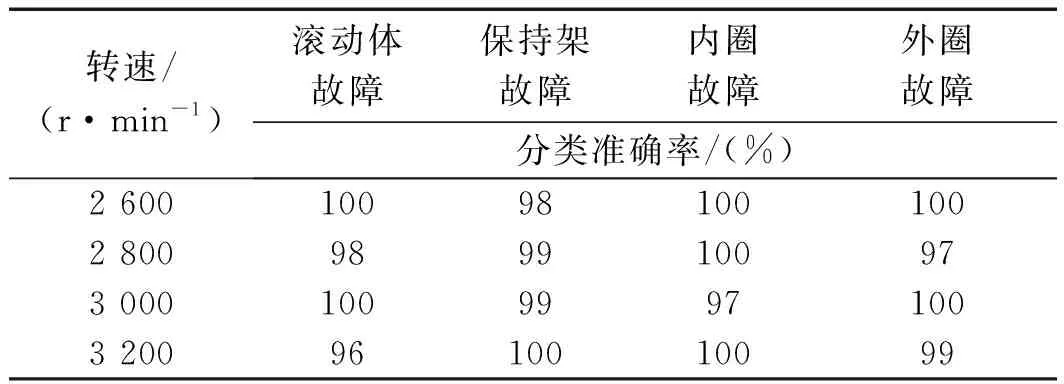
表2 随机森林不同转速下故障辨识结果

从表2中看出:在不同转速下,随机森林对几种故障状态的分类准确率都比较高。

3.2 不同分类器的辨识精度对比

为了验证随机森林法在故障辨识精度上的优越性,笔者将该算法获得的分类准确率与分类器,即BP神经网络(back propagation neural network,BPNN)、k近邻分类(k-nearest neighbor classification,KNN)、支持向量机(support vector machines,SVM)获得的分类准确率进行了对比。

不同分类器的分类结果如表3所示。

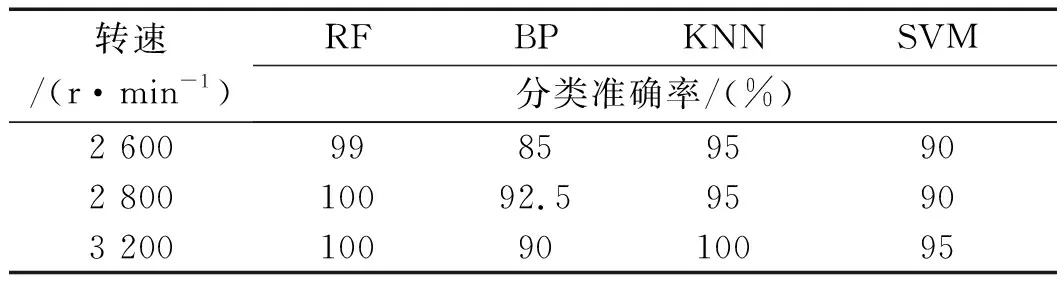
表3 不同分类器的分类准确率

从表3中可以看出:

在不同转速下,随机森林的分类准确率高于其他3种分类方式。这是因为相比传统的分类器BP、KNN、SVM,随机森林不需要繁琐的参数寻优过程和最优的特征向量选择;

同时,随机森林算法可以利用简单的弱分类器(决策树),以投票的形式产生最终的分类结果,从而可以有效地提高诊断的精度。

3.3 变工况下随机森林法的辨识精度

在变工况和转速波动条件下,为了验证随机森林方法的辨识精度,笔者分别选择2 600 r/min～2 800 r/min,2 800 r/min～3 000 r/min,3 000 r/min～3 200 r/min,2 600 r/min～2 800 r/min～3 000 r/min的4个转速范围对随机森林方法的辨识性能进行验证。

在变工况下,随机森林分类识别率如表4所示。

表4表明,在转速波动时,随机森林方法仍然具有较高的辨识精度。

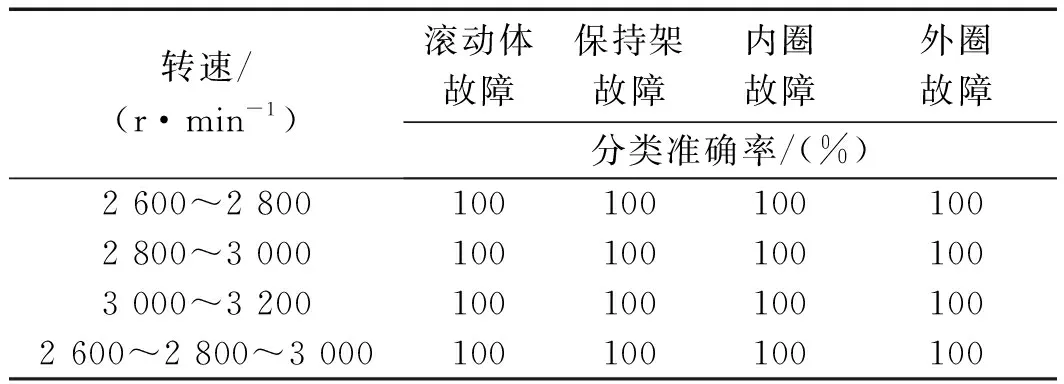
表4 随机森林在变工况下分类准确率

3.4 不同训练样本数下随机森林法的辨识精度

为了进一步测试不同训练样本数目对随机森林法故障辨识精度的影响,笔者随机设置训练样本数目分别为10、15、20、25、30,经测试,得到了不同训练样本数目与故障识别率的关系,如图6所示。

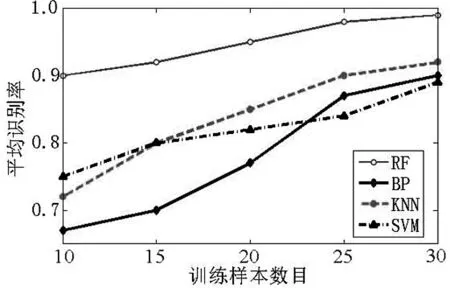
图6 不同训练样本比例对应的平均识别正确率

从图6可以看出:

(1)随着训练样本数目的增加,几种分类器故障识别准确率不断增大;

(2)在训练样本数较少的情况下,随机森林分类识别准确率一直保持稳定,而其他传统分类器的故障分类准确率则受训练样本数目的影响较大。

3.5 不同分类器的抗噪性对比

由于在实际情况下采集到的滚动轴承振动信号往往伴随噪声等干扰信息,为了验证随机森林法的抗干扰能力,笔者在所建立的测试集中加入随机扰动。

扰动矩阵定义为M=0.2*F(120,16),F为随机函数,旨在产生区间为[0,1]的随机数;120表示测试样本的数量为120个,16表示测试集特征参数的个数为16个。

各分类方法故障识别率如图7所示。

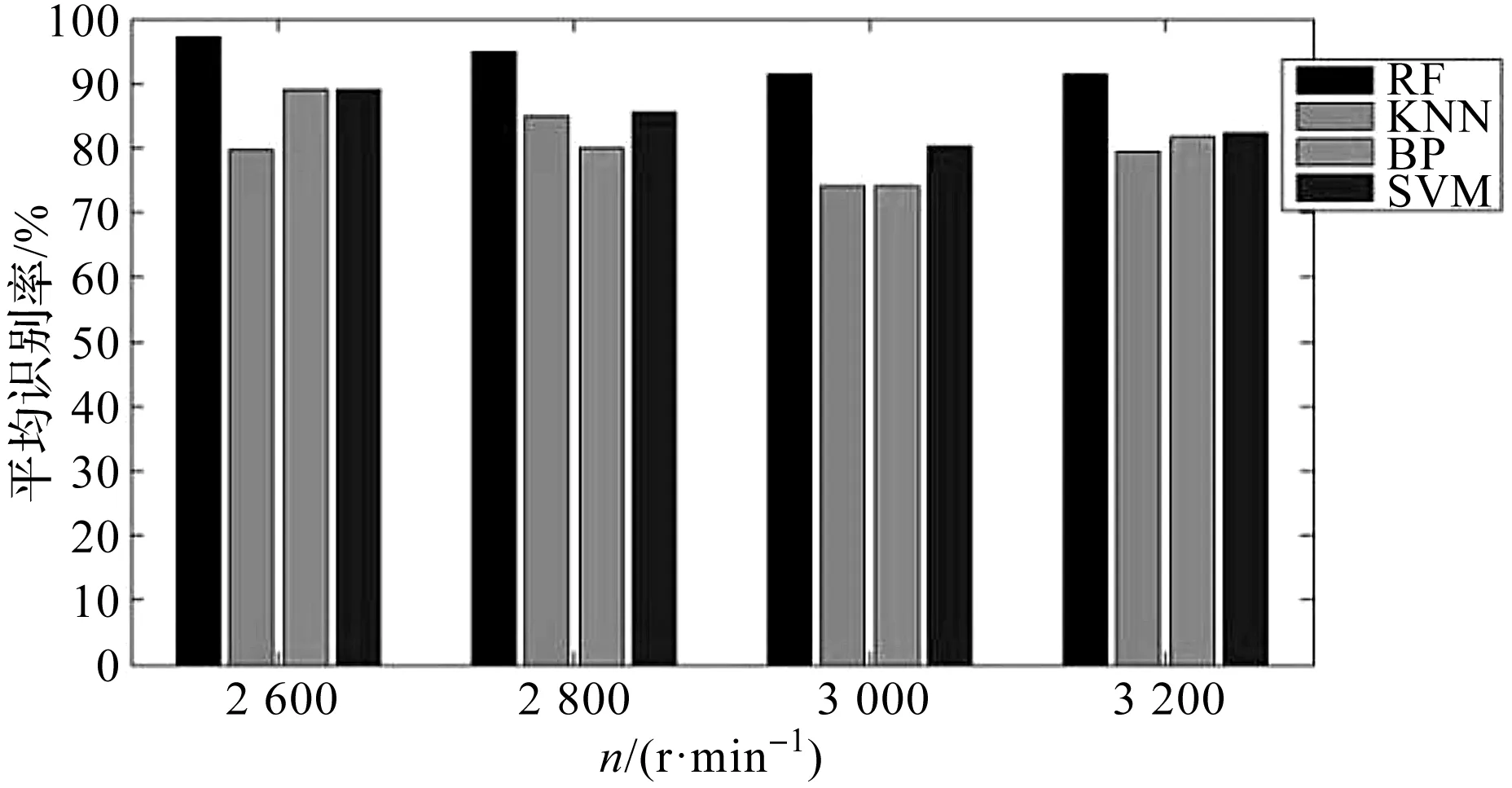
图7 各分类方法在抗噪性方面的对比

图7结果表明:

与传统的分类方法相比,随机森林具有更好的抗噪声等干扰能力。

由此可见,笔者提出的方法在滚动轴承故障辨识方面有良好的工程实用价值。

4 结束语

针对滚动轴承故障诊断中存在的特征选取困难,以及分类精度较低的问题,笔者提出了一种基于随机森林的滚动轴承故障辨识方法。首先,提取出滚动轴承振动信号中的时域特征,将其作为特征向量;然后,以这些特征向量作为随机森林算法的输入,对轴承进行了故障诊断;最后,利用SQI实验平台轴承数据,对该方法的可行性与有效性进行了验证。

研究结果表明:

(1)在不同转速下,随机森林对几种故障状态分类准确率都比较高;并且在变工况和波动转速下,随机森林方法也具有良好的辨识性能;

(2)在不同转速下,与BP、KNN、SVM 3种分类方式相比,随机森林的分类准确率更高;

(3)在样本数目较少的情况下,随机森林仍然能保持稳定的分类识别率;

(4)相较于BP、KNN、SVM分类器,随机森林算法具有良好的抗噪声干扰能力。

在VMD的分解中,分解个数K值的选择直接决定着VMD分解的结果,因此,在后续的工作中,笔者将对如何合理有效地选取K值做进一步的研究。