基于相关支持矩阵机的滚动轴承故障诊断方法研究*

陈 英,陈木荣

(1.长沙民政职业技术学院 电子信息工程学院,湖南 长沙 410004;2.华南理工大学 机械与汽车工程学院,广东 广州 510640;3.广东理工学院 机电工程系,广东 肇庆 526100)

0 引 言

滚动轴承是旋转机械设备中必不可少的重要零件,其状态的好坏直接影响整个机械设备的安全运行。因此,对滚动轴承工作状态的监测及其故障识别一直是学者们的研究热点。

随着对滚动轴承状态判别算法研究的不断深入,各种故障识别器被应用于滚动轴承故障识别领域,并取得了一定的效果[1,2]。

随着模式识别算法的快速发展,各种分类器(算法)被广泛应用于滚动轴承状态识别中,如支持向量机(support vector machine,SVM)、线性判别分析、k近邻、贝叶斯分类器、极限学习机(extreme learning machine,ELM)等[3-8]。

上述经典分类器是在输入特征为向量形式的基础上构造的。而在实际应用中,拾取的滚动轴承振动信号记录了一段时间内的波动信息,使其以二维矩阵的形式得以表现出来。为适应传统分类器对输入数据的形式要求,通常需要将拾取的特征矩阵重塑为向量,或以向量形式提取特征。然而,由于二维振动信号行和列之间的高度相关性,矢量化会破坏特征矩阵的列或行之间的结构信息[9]。

为了解决上述问题,LUO Luo等人[10]提出了一种新的支持矩阵机(support matrix machine,SMM),它可以充分利用特征矩阵的结构信息,采用交替方向乘子法,来优化SMM的目标函数,获得良好的分类效果。

此外,在SMM的基础上,相关学者又陆续提出了一系列的改进算法。ZHENG Qing-qing等人[11,12]提出了多分类支持矩阵机(multiclass support matrix machine,MSMM)和稀疏支持矩阵机(sparse support matrix machine,SSMM);PAN Hai-yang等人[13]提出了辛增量矩阵机(symplectic incremental matrix machine,SIMM);YE Yun-fei等人[14]提出了多距离支持矩阵机(multi-distance support matrix machines,MDSMM);LI Xin等人[15]提出了辛加权稀疏支持矩阵机(symplectic weighted sparse support matrix machine,SWSSMM)。

SMM及其改进算法都是以矩阵形式对滚动轴承的含噪信号、冗余特征等进行分类,可以完成不同工况下的分类问题。

随着SMM算法的理论和应用研究的不断增加,该方法的一些不足之处也逐渐显现出来,如结果缺乏必要的概率信息,预测的结果不具有统计意义,预测结果的不确定性无法估算,等。同时,随训练样本集的规模增大,采用该方法所获得的支持向量的个数也呈线性增长,这使得模型的稀疏性有限[16]。

鉴于SMM的不足,笔者结合再生核希尔伯特空间(reproducing kernel Hilbert space,RHKS)[17],并利用贝叶斯统计方法进行推理,提出了一种相关支持矩阵机(relevance support matrix machine,RSMM)。

与SMM方法相比,RSMM是一种基于贝叶斯框架的统计学习方法,该方法利用贝叶斯学习框架,为模型参数施加一个条件概率分布的约束,可以得到稀疏的解空间。同时,在SMM方法中,只有满足Mercer条件限制的核函数,才可以用来构造非线性的SMM。由于RSMM是以贝叶斯统计框架构造的模型,其核函数不受Mercer条件限制,可以获得各类别之间的概率统计信息,从而可以对不确定样本进行分类。

此外,多核函数的引入可以解决由多个不同数据源带来的复杂问题;将先验概率引入到模型权重设置中,利用超参数对权重进行一对一分配,可使多数权值的后验分布近似于零。由此可以说明,RSMM模型是稀疏的,且在复杂数据模式识别中,在特征提取的多元化和异常数据的多样性方面,该方法具有较好的适用性。

综上所述,笔者在矩阵多元化和贝叶斯框架的基础上,提出一种RSMM算法,来获得各类别之间的概率统计信息,进而对不确定样本进行分类;最后,进行滚动轴承故障分类实验,采用滚动轴承数据集对该方法的性能进行检验。

1 相关支持矩阵机

样本数据集为:

ZC={Zi,yj|Zi∈RS×N}

(1)

式中：C—类别数;S—样本数;N—每个样本的长度。

其中:i=1,2,…,N;j=1,2,…,C。

针对式(1),引入初始辅助变量Y∈RS×C和权矩阵W∈RS×C,笔者构造标准噪音回归模型如下:

ysc|wc,ks～Nysc(kswc,1)

(2)

式中:ysc—Y的第s行c列的元素;wc—W的第c列;Nysc(kswc,1)—ysc服从均值为kswc,方差为1的正态分布;ks—特征集数。

ZC核函数K的行也代表训练集中第s个样本数据与其他样本数据的相似度。引入多项概率链接函数,可以将回归目标转化为类别标签,即:

ts=i,ysi>ysj(i≠j)

(3)

因此,根据多项概率似然函数原理,其分类表达式可以表示为:

(4)

式中:u—服从N(0,1)分布;Φ—高斯累积分布函数。

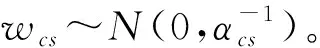
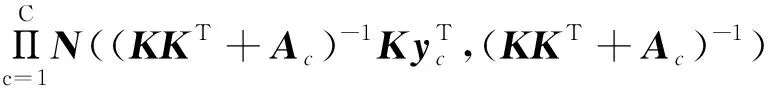
(5)

式中:Ac—由A的c列对应的对角矩阵。

由log边缘似然函数可以推导出:

(6)

式中:C=I+QA-1QT。

C可以分解为:

(7)

式中:C-i—删除第i个样本后的C值。由此可以得出:

(8)

Log边缘似然函数可被分解为:

L(α)=L(α-i)+l(αi)

(9)

式中：ei—稀疏因子;gci—量化因子。

通过求解∂L(A)/∂αi=0,可得驻点αi。

在模型训练过程中,由最大后验概率估计的方法可得:

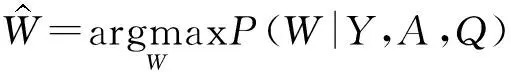
(10)

因此,给定类别时,基于最大后验概率的权重更新方法为:

(11)

根据上式,对于第i类,其辅助变量表达式为:

(12)

先验参数的后验概率分布的表达式为:

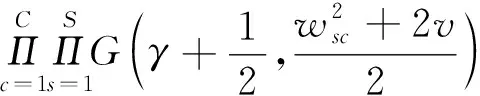
(13)

通过更新和训练,模型参数W的大部分值为0,因此,模型在样本空间和特征空间上均是稀疏的。对于新的样本Znew,利用后验概率式(4)可得:

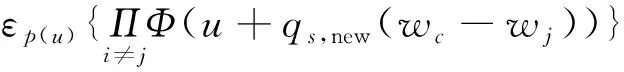
(14)

式(14)即为新样本属于类别c的概率。而最大概率对应的类别即为新样本所属的类别,即:

(15)

2 基于RSMM的诊断方法

为了验证RSMM方法在滚动轴承故障诊断上的有效性,笔者将利用美国凯斯西储大学的滚动轴承数据和湖南大学的滚动轴承试验数据来进行分析与验证。

首先,将利用美国凯斯西储大学数据(故障分类常用数据集)的7种状态,来证明RSMM在识别率、分类效率和小样本等方面与其他方法相比有更好的分类性能;

其次,将利用湖南大学的试验数据(实验数据具有6种状态类型),来进一步验证RSMM的普适性;

最后,为了验证RSMM方法的优越性,选择MSMM、SSMM和SIMM进行对比分析。

由于RSMM、MSMM、SSMM和SIMM等方法的输入元素为矩阵,需要构造输入矩阵来完成分类和建模。多重同步压缩变换(multi-synchro squeezing transform,MSST)作为一种新的信号分析方法,已被证明具有良好的特征提取能力。因此,在此处笔者采用MSST来分析原始信号,以获得可以保存完整结构信息的特征矩阵。

实验的具体步骤如下:

(1)将不同状态(一维时间序列)的样本进行MSST分析,对得到的时频谱进行灰度化和下采样,获得输入特征矩阵;

(2)将训练样本特征矩阵输入到主程序(MATLAB)中,得到决策函数式(15);

(3)将测试样本输入决策函数,得到预测结果;

(4)对各模型的预测结果进行分析,得到各模型的输出识别状态。

3 实验及结果分析

3.1 凯斯西储大学数据验证

为了验证所提方法的有效性,笔者首先利用美国凯斯西储大学滚动轴承数据进行测试。实验选择的滚动轴承型号为SKF6205。

轴承故障模拟试验台如图1所示[18]。

图1 滚动轴承故障模拟试验台

为了模拟滚动轴承的各种故障状态,笔者采用电火花加工技术,分别在滚动轴承的内圈、外圈和滚动体上加工出裂纹。

实验中,采样频率设置为48 000 Hz,电机转速设置为1 730 r/min,负载为2.24 kW。笔者在每种状态下(正常、内圈故障、外圈故障、滚动体故障,故障宽度0.457 2 mm)各采集200个样本(每个样本2 048点)。

实验环境详细设置如表1所示。

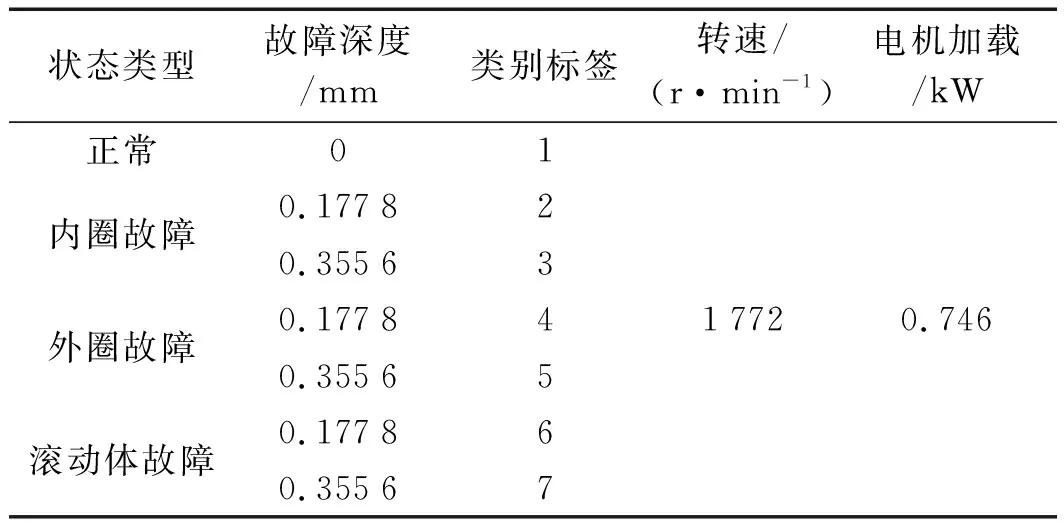
表1 实验环境设置

笔者随机抽取100个样本进行训练,100组作为测试样本。

笔者采用MSMM、SSMM、SIMM和RSMM方法分别对滚动轴承实验数据进行训练和测试。4种方法识别结果的混淆矩阵如图2所示。

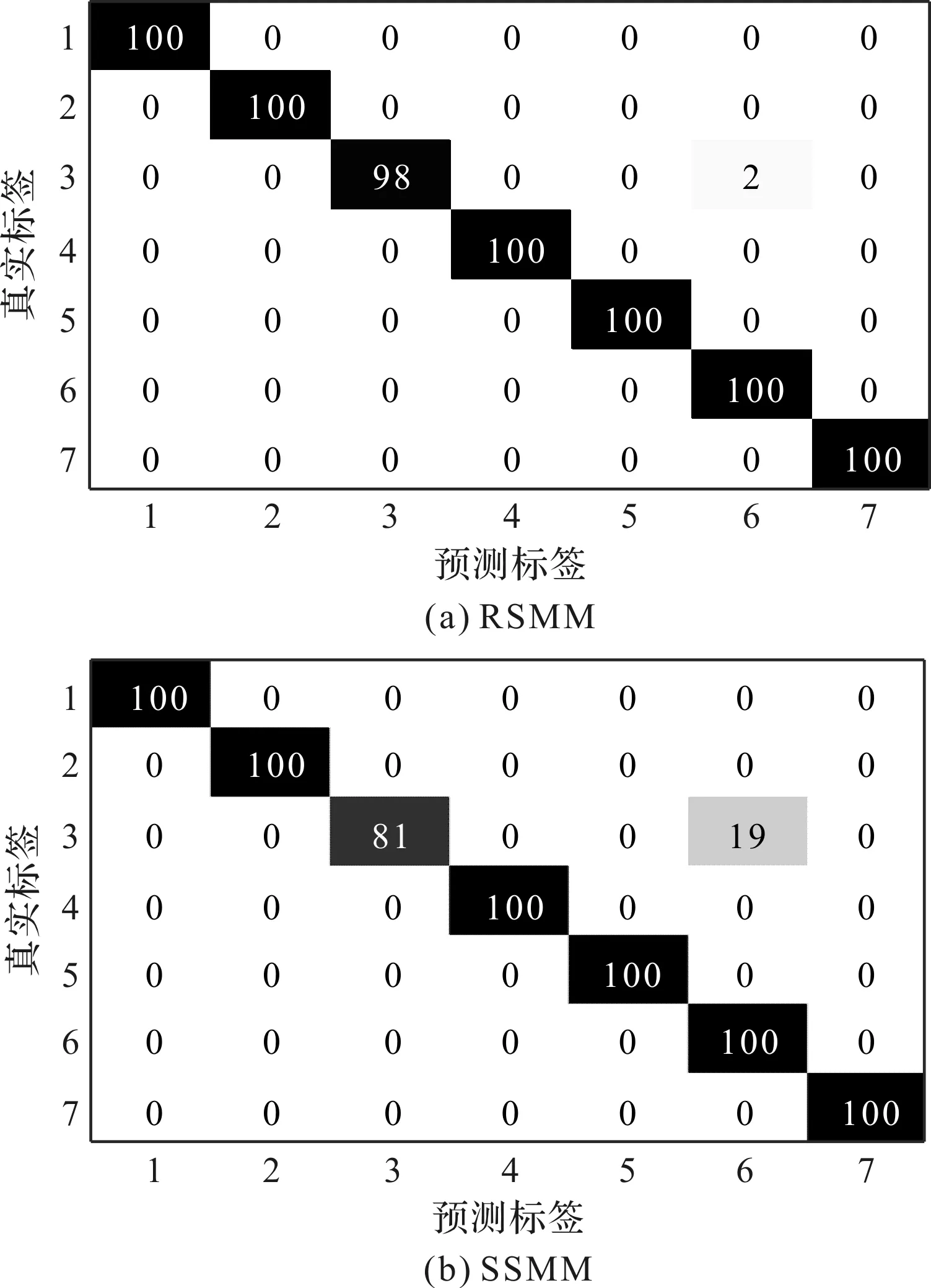
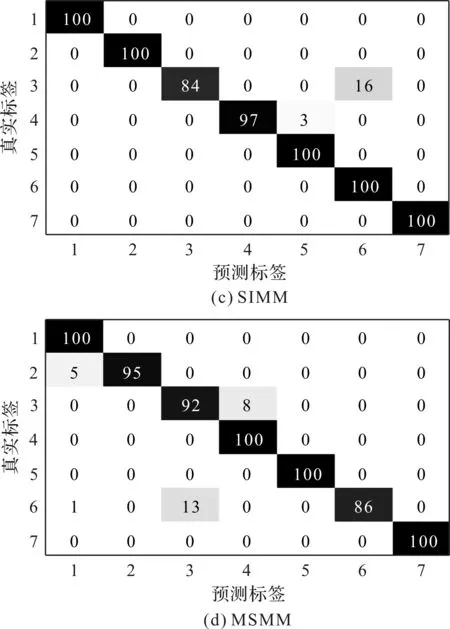
图2 4种方法识别结果的混淆矩阵1，…，7—滚动轴承状态类别标签;横坐标—训练样本的预测标签;纵坐标—训练样本的真实标签

从图2可以看出:(1)在所有方法中,采用MSMM的故障诊断效果最差,这是由于MSMM对数据的要求较高,数据复杂度和数据长度会导致MSMM难以收敛;(2)与MSMM相比,SSMM和SIMM在鲁棒性和冗余性方面具有一定的优势,可以得到更好的分类结果。

但是上述方法的结果缺乏必要的概率信息,预测的结果不具有统计意义,预测结果的不确定性无法估算;同时,该方法获得支持向量的个数基本上随训练样本集的规模呈线性增长,模型的稀疏性有限。

与MSMM、SSMM和SIMM相比,RSMM方法采用核函数获得信号的传输特性,并利用概率框架和先验概率来确定最可能的状态类别。因此,RSMM方法具有更优越的性能。

为了进一步验证RSMM方法分类的客观性,笔者进行5次随机分类实验,即在每个实验中,随机抽取100组样本进行训练,100组作为测试样本。

4种方法的识别结果如图3所示。

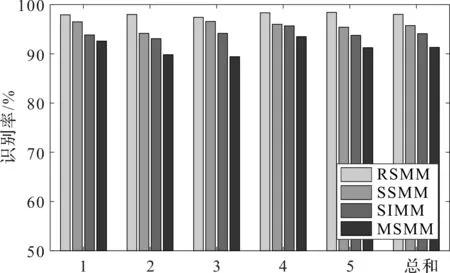
图3 4种分类方法的分类结果1—5—第1—5次随机分类实验

从图3可以看出:在5次随机分类实验中,RSMM的分类效果最好,RSMM方法具有优越的分类性能。

全面评价一种分类方法的分类性能,需要从多个角度进行验证。因此,笔者选取查准率、召回率、F-score、kappa、准确率等指标进行再次验证。在一定范围内,以上5种指标值越大,说明模型的分类性能越好。

各项指标说明如下:

(1)Accuracy为正确率,作为最常用的分类指标,表示分类正确样本在总体样本中所占比例;(2)Recall表示召回率,表示在所有正确分类样本中,正类样本所占比例;(3)Precision表示精确率,表示真正能被模型识别出来的属于正类的样本占比;(4)F1-score为精确率和召回率的调和值;(5)kappa系数常用于一致性检验。

同样,笔者为了克服偶然因素,进行了5次随机实验,实验结果如表2所示。

表2 4种方法分类性能比较(平均值±标准)

从表2可以看出:在各个指标上,RSMM方法都优于其他分类方法,表现出了优越的分类性能。这是因为RSMM方法在贝叶斯框架下进行学习,其核函数不受Mercer条件限制,能够直接完成多分类问题,且不同核函数的引入有效地解决了不同数据源的数据复杂性问题,提高了算法的分类精度;而SSMM、SIMM、MSMM方法在分类较多、数据较复杂的情况下,分类能力不足。

除了识别率外,分类效率也是评价机器学习方法的一个重要指标。

笔者随机抽取100个样本作为训练样本,其余100个样本作为测试样本。从原始信号的输入到分类结果的输出,记录整个分类过程所消耗的时间。

4种分类方法的分类效率如表3所示。

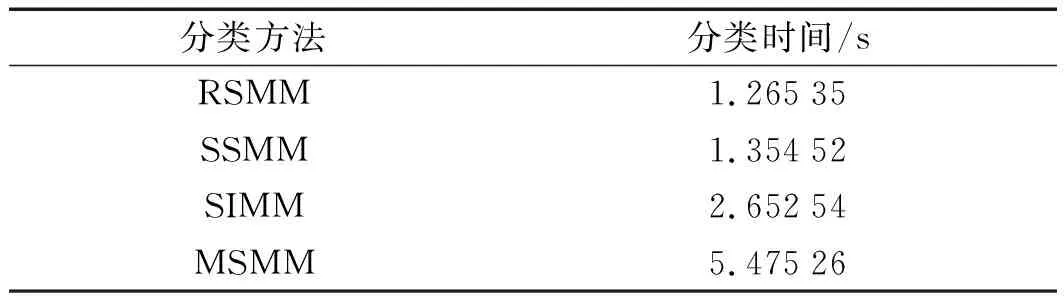
表3 4种分类方法的分类效率对比

由表4可知,利用美国凯斯西储大学滚动轴承数据集,验证了RSMM方法的优越性。

3.2 湖南大学数据验证

为了进一步说明RSMM方法的普适性,笔者再次选择湖南大学滚动轴承数据集进行验证[19]。

该滚动轴承故障模拟试验台如图4所示。

图4 滚动轴承故障模拟试验台

实验环境设置如表4所示。

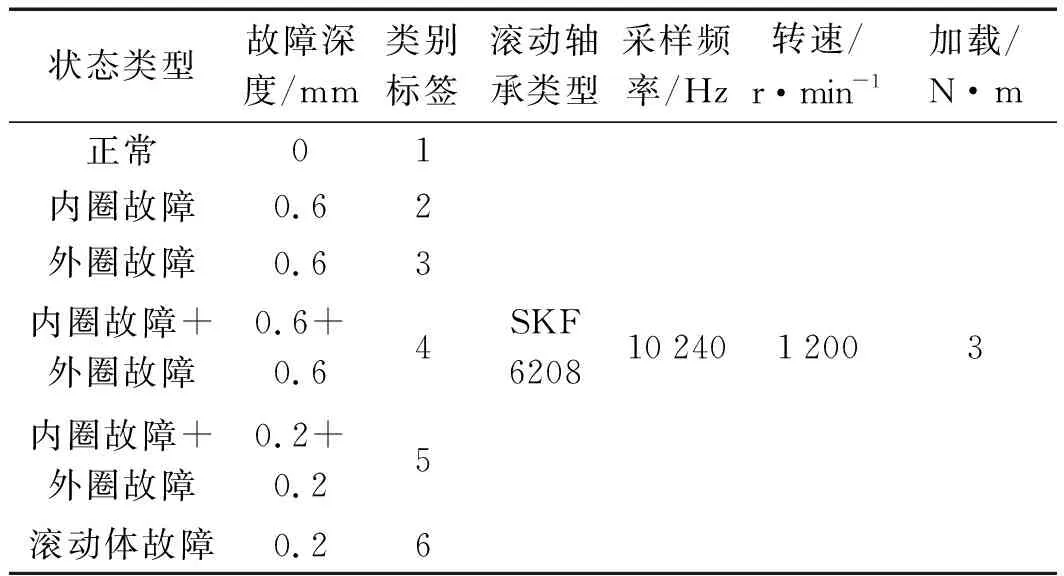
表4 实验环境设置

在实验过程中,笔者随机抽取100组样本(每个样本1 024个点)进行训练,100组作为测试样本。

4种方法的分类识别结果如图5所示。

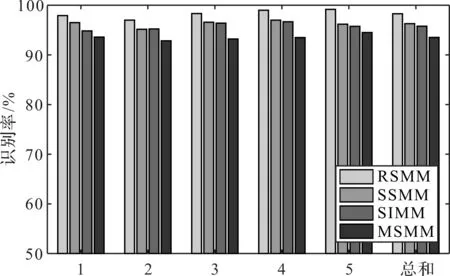
图5 4种分类方法的分类结果

从图5可以看出:在5次随机实验中,RSMM的分类效果仍然最好。该结果进一步证明了笔者所提出的方法的优越性。

为了全面评价该方法的分类性能,笔者仍然选取查准率、召回率、F-score、Kappa、准确率等指标,同时选择SSMM、SIMM、MSMM 3种分类方法进行对比分析,以验证RSMM方法在5种指标下的优越性能。

为了克服偶然因素,笔者独立进行5次随机实验。

4种方法分类性能比较的实验结果如表5所示。

表5 4种方法分类性能比较(平均值±标准)

综上所述,根据Accuracy、Recall、Precision、F-score和Kappa等衡量指标下的对比结果可知,在以上4种方法中,RSMM方法的识别结果明显要优于SSMM、SIMM和MSMM方法。

分析原因可知:

(1)RSMM是一种基于贝叶斯框架的统计学习方法,该方法在贝叶斯框架下进行模型训练,其核函数不受Mercer条件限制,可以获得各类别之间的概率统计信息,进而可以对不确定样本进行分类;

(2)MSMM是一种平行超平面分类器,当输入数据包含多种复杂特征信息时,数据的复杂性和数据的长度会导致MSMM难以收敛;

(3)采用SSMM和SIMM构建模型的前提是回归矩阵具有低秩特性,在面对大多数矩阵是多秩的情况下,SSMM和SIMM方法很难发挥其模型本身的优势。

相比SSMM、SIMM和MSMM方法,RSMM方法是借助于贝叶斯框架思想构造出来的概率统计模型,因此,在采用该方法对不确定样本(尤其是复杂数据问题)进行分类时,RSMM具有明显的优势。

4 结束语

为了解决采用支持矩阵机(SMM)进行分类建模时,缺乏必要的概率信息,而导致其产生的稀疏性和鲁棒性不明确的问题,笔者以贝叶斯理论框架为基础,提出了一种相关支持矩阵机(RSMM),来获得各类别之间的概率统计信息,进而对不确定样本进行了分类;最后,进行了滚动轴承故障分类实验,采用滚动轴承数据集对该方法的性能进行了检验。

研究结论如下:

(1)RSMM以样本信号矩阵作为分类器的输入,在建模中引入概率框架和先验概率,使预测结果具有必要的概率信息,并且使预测结果具有统计意义;

(2)在贝叶斯框架下,采用RSMM方法进行模型训练,其核函数不受Mercer条件的限制,可以获得各类别之间的概率统计信息,进而可以对不确定样本进行分类;

(3)滚动轴承故障分类实验证明,在在Accuracy、Recall、Precision、F-score和Kappa等各项衡量指标方面,RSMM方法均表现出其良好的性能。

由于RSMM方法在滚动轴承故障诊断方面具有良好的表现,可以将其推广到其他旋转机械的故障诊断中。然而,RSMM方法仍然存在一些需要改进的地方,如特征冗余性等。

因此,在今后的工作中,笔者所在课题组将对建模过程中的特征冗余性问题进行研究,以进一步提高该算法的识别精度。