基于SVD和SET的滚动轴承故障诊断研究*
于 湘,方玉峰,高 煜,陈 光,夏伶勤
(浙江机电职业技术学院 增材制造学院,浙江 杭州 310053)
0 引 言
如今,机械设备正逐步朝着精密化及智能化方向发展,机械零部件在机械设备运转过程中起着重要作用。滚动轴承是旋转机械的核心部件,它一旦发生故障会造成机械设备的损伤,不仅会造成巨大的经济损失,其损伤严重时还可能会造成人员伤亡。因此,对滚动轴承进行故障诊断工作是非常有必要的[1-3]。
目前,对滚动轴承的故障进行诊断的方法有很多种,其中非常常见是基于振动信号的方法[4]。由于轴承在运转过程中会受到诸多干扰,导致所采集到的振动信号中,不仅包含轴承相应的特种成分,还包含大量的噪声。因此,轴承振动信号是一种典型的非线性、非平稳信号。
采用时频分析方法可以有效地处理此类非线性、非平稳信号。常用的时频分析方法主要有:短时傅里叶变换(short-time Fourier transform,STFT)[5]、Wigner-Ville时频分布(Wigner-Ville distribution,WVD)[6]和小波变换(wavelet transform,WT)[7]等。这类方法都属于传统的时频分析方法,都有各自的弊端,而且它们还有一个共有问题,即时频聚集性不高。
近年来,时频后处理算法逐步进入人们的视野。2017年,YU Gang等人[8]提出了一种新的时频后处理方法,即同步提取变换(SET)。该方法在短时傅里叶变换(STFT)的基础上,建立起了一种同步提取算子,仅提取时频脊线位置处的时频系数,因而能大大地提高时频聚集性。
奇异值分解(singular value decomposition, SVD)在工程中常常被用作一种降噪的手段,它可以有效去除信号中的噪声。王琛[9]将轴承振动信号用SVD进行了降噪处理,再结合神经网络,提出了一种新型的滚动轴承故障诊断方法。朱丹等人[10]首先在MOMEDA方法中引入了SVD,用来去除背景噪声,然后再进行了算法优化,仿真信号和试验数据分析表明,该方法能对高速列车齿轮箱轴承进行有效的故障诊断。
SVD主要用来对一维信号进行降噪,其中关键的一个环节就是构造合适的数据矩阵。时频分析处理的结果是一个数据矩阵,可以将其放入SVD算法中。文献[11-13]中,用S变换的时频谱图替换了SVD中的数据矩阵,实现了对二维时频谱图进行降噪,并在实际故障诊断中也取得了不错的效果。
该研究提出一种SVD和同步提取变换(SET)相结合的滚动轴承故障诊断方法。首先,笔者对轴承振动信号进行同步提取变换,得到时频谱图;再用SVD对其进行降噪处理,重构波形,包络解调,得到具有故障特征频率的包络谱;最后,将该方法与只进行同步提取变换的方法进行对比,来验证该方法的优越性。
1 理论基础
1.1 同步提取变换
同步提取变换(SET)是一种时频分析后处理技术,以STFT为理论框架,是一种能有效提高时频聚集性的先进方法[14]。
信号s(u)的STFT定义如下:
(1)
式中:g(u-t)—可移动窗函数;u—时间;ω—频率;t—位移因子。
根据帕塞瓦尔定理,式(1)可以写为:
(2)
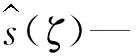
对式(2)进行变换与修正,可以得到:
(3)
定义频率为ω0的一个信号,其解析式可以写为:
s(t)=A·eiω0t
(4)
将式(4)代入到式(3)中,则可以得到:
(5)
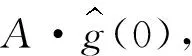
根据上述公式,可以估计出信号的瞬时频率为:
(6)
式中:∂tGe(t,ω)—Ge(t,ω)对时间的一阶偏导数。
根据式(6),提取STFT时频谱在瞬时频率处的时频系数。该过程被称为同步提取变换(SET)。
它的表达式可以写为:
Te(t,ω)=Ge(t,ω)δ(ω-ω0(t,ω))
(7)
式中:δ(ω-ω0(t,ω))—同步提取算子(SEO)。
采用该方法可以进行信号重构,重构信号的公式可以表示为:
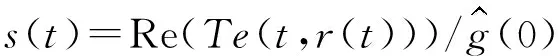
(8)
式中:Re(·)—取实部。
1.2 奇异值分解
在数学领域,奇异值分解(SVD)是一种对矩阵进行分解的方法。它被广泛应用于故障的诊断领域,起着去除噪声的作用,因而具有很重要的应用价值[15-17]。
设一个实矩阵L∈Rm×n,必定存在两个正交矩阵:U=(u1,u2,…,um)∈Rm×m和V=(v1,v2,…,vn)∈Rn×n,使得:
L=UAVT
(9)
其中,A=(diag(σ1,σ2,…,σq),0)或者其转置,且为对角矩阵,这取决于m
在这些奇异值中,前几个较大的奇异值主要反映的是特征信号,其余则反映噪声,把这些较小的奇异值置0,再反变换回去,就可以达到去除噪声的作用。
设有Y=(y(1),y(2),…,y(N))为离散数字信号,可以构造Hankel矩阵如下:
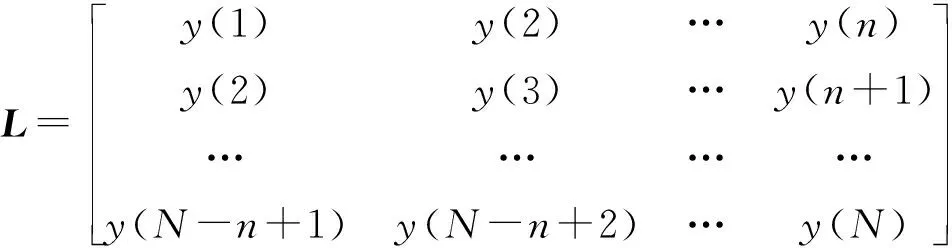
(10)
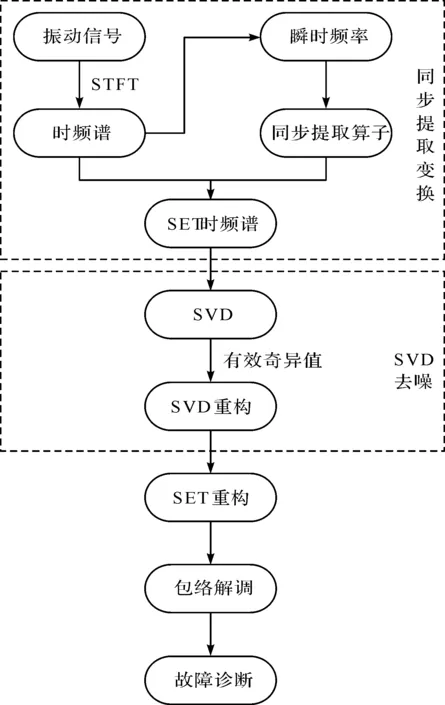
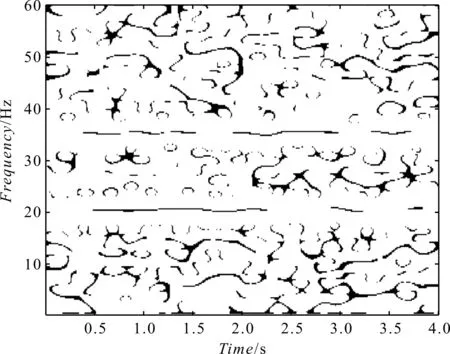
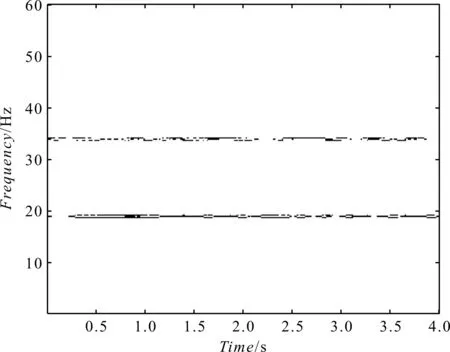
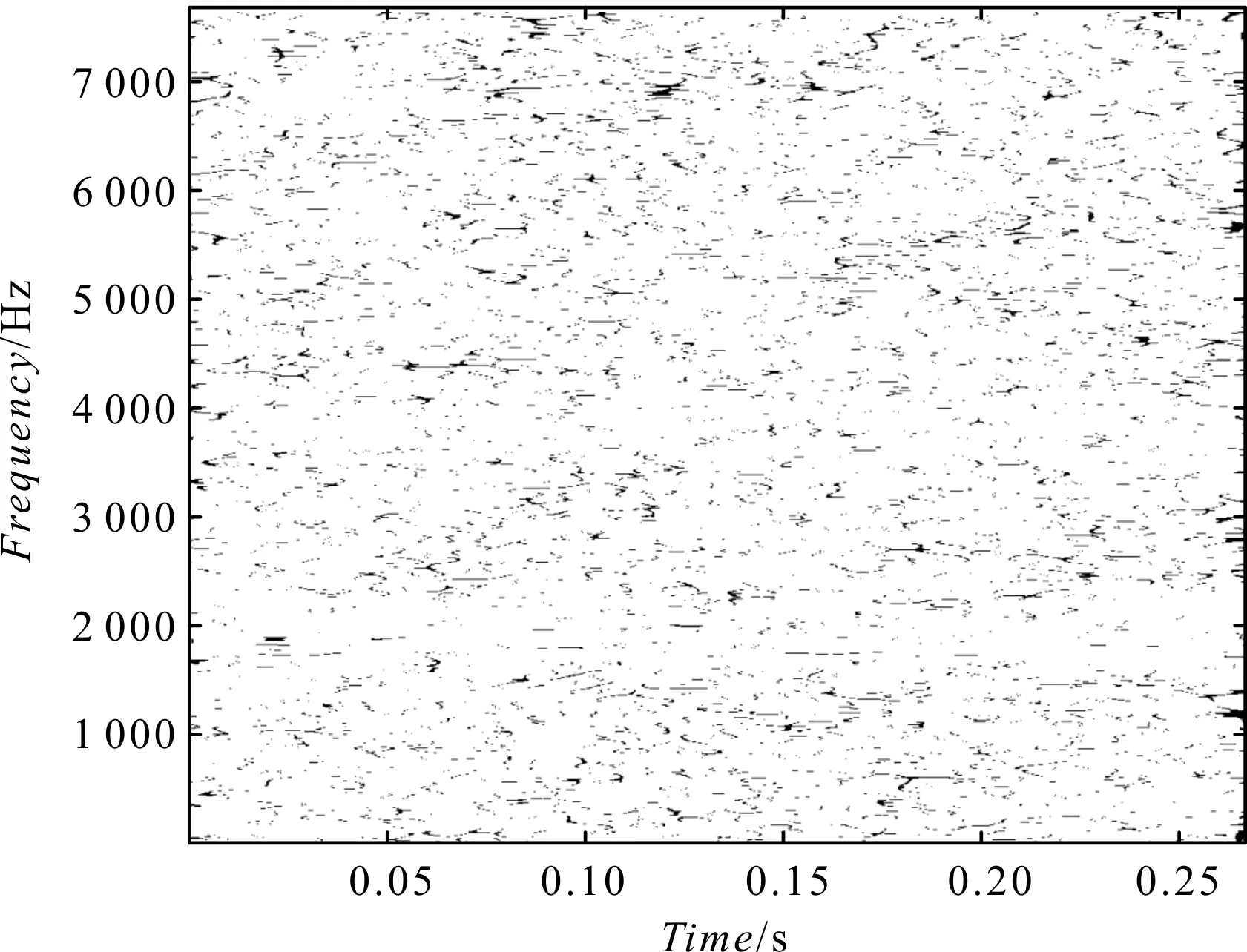
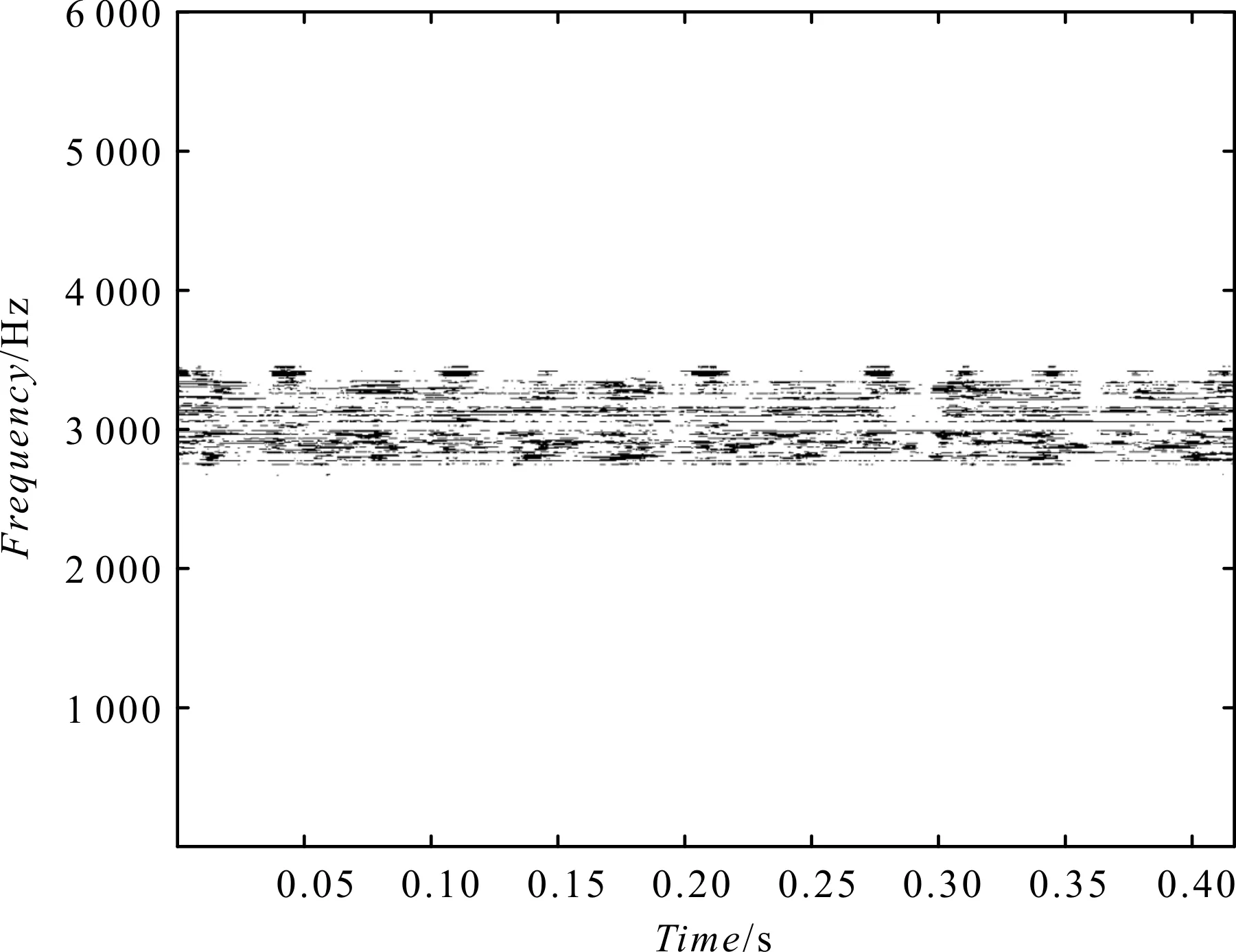
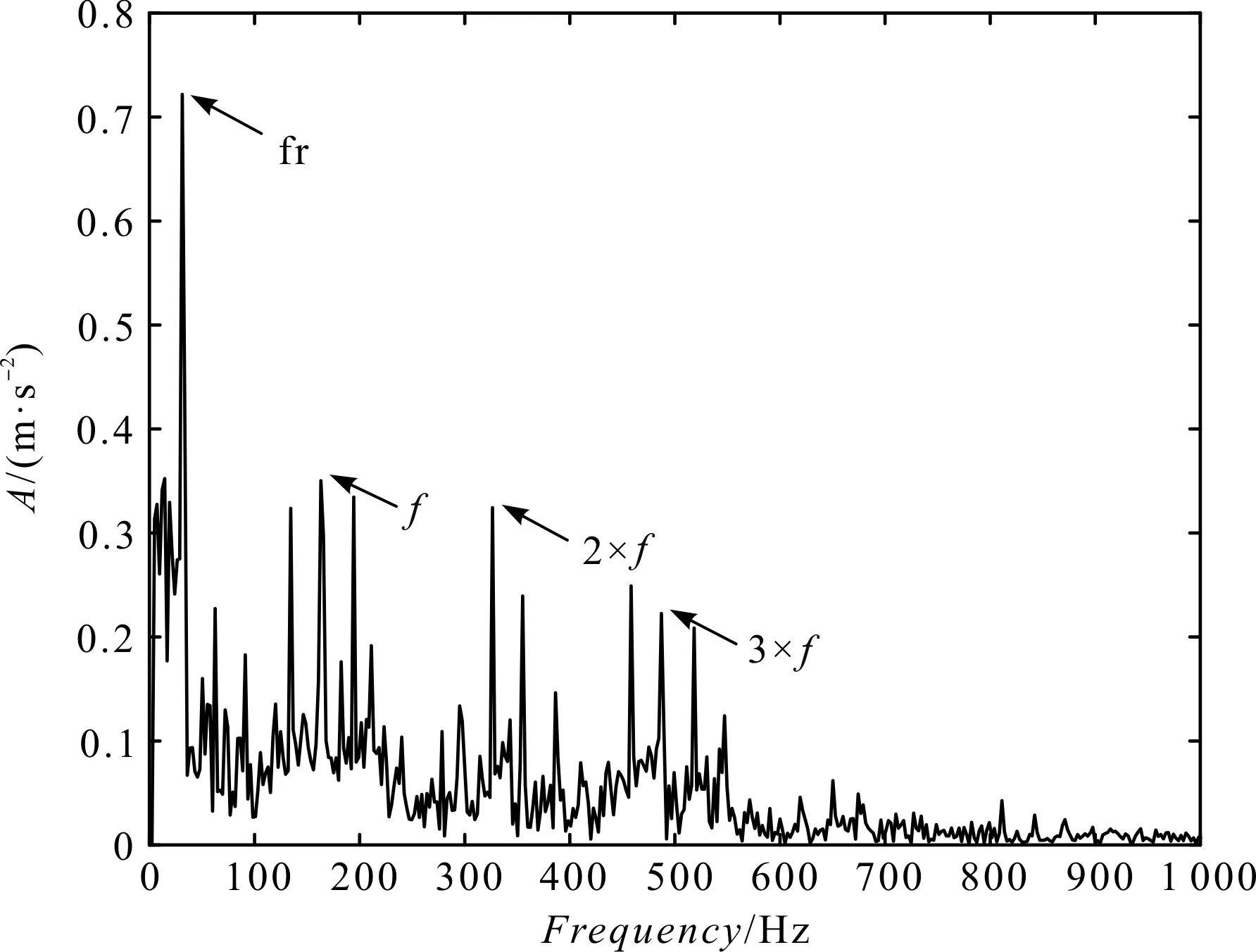
式中:1 基于SVD和SET的滚动轴承故障诊断实现流程如图1所示。 图1 SVD与SET结合的故障诊断方法流程 对采集到的轴承振动信号进行诊断分析的具体步骤如下: (1)STFT,得到时频谱; (2)通过估计信号的瞬时频率,构造同步提取算子,并将其作用于STFT时频谱,得到SET时频谱; (3)用SET时频谱代替SVD中的Hankel矩阵,得到奇异值序列,通过选取有效的奇异值,进行SVD重构,达到SET时频谱去噪的效果; (4)SET时频谱重构得到时域信号,进行包络解调,得到包络谱,最后进行轴承故障诊断。 笔者构造了一个简单的信号,并用SET方法和SVD与SET相结合的方法对该信号进行处理,通过处理结果的对比,来验证该方法的优势。 构造的信号表达式为: x(t)=sin(2π·20t)+sin(2π·35t) (11) 信号的采样频率为120 Hz,采样时间为4 s的时域波形如图2所示。 图2 时域波形 该信号由频率为20 Hz和频率为35 Hz的谐波信号简单叠加组成,并在此信号中,笔者加入信噪比为2 dB的高斯白噪声。 笔者采用SET方法对该信号进行处理,其结果如图3所示。 图3 SET时频谱图 从图3中可以看到:信号瞬时频率周围存在着大量的噪声,使得时频谱图看起来较为混乱,可读性较差。 在图3的基础上,笔者进行SVD分解,得到的奇异值序列如图4所示。 图4 奇异值序列 笔者选取前3个有效的奇异值进行了SVD重构,重构后的结果如图5所示。 图5 基于SVD的SET时频谱图 对比图3和图5可以发现:图3中的大部分噪声得到了去除,图5中仅保留了信号的瞬时频率20 Hz和35 Hz,而且时频谱图十分清晰,可读性较高。 通过该简单的对比可以发现:SVD和SET相结合的方法能有效去除噪声,而且可以提高时频谱图的可读性。 接下来,笔者将使用滚动轴承外圈和内圈的故障数据,对基于SVD和SET相结合方法的有效性进行验证。 此处所使用的滚动轴承故障试验系统如图6所示。 图6 轴承故障试验系统 该系统主要由模拟轴承故障的试验台、压电式加速度传感器、MI6008型数据采集分析仪和笔记本电脑等组成。 在进行测试实验时,笔者先安装正常轴承,再安装故障轴承;启动设备进行试验数据采集,将采集到的数据传到电脑中,进行数据处理分析[18-20]。 该次使用的故障轴承型号为6307,电机转速为1 496 r/min,采样频率为15 360 Hz。 故障轴承的具体参数如表1所示。 表1 故障轴承参数 笔者使用轴承外圈故障的数据。外圈故障信号的时域波形如图7所示。 图7 时域波形 笔者先用SET处理该振动信号,其结果如图8所示。 图8 SET时频谱图 从图8中可以观察到:滚动轴承的故障信息完全被噪声所淹没,时频谱图完全识别不到有效的信息。 然后,笔者对图8进行SVD降噪,其结果如图9所示。 图9 基于SVD的SET时频谱图 从图9中可以发现:通过SVD降噪去除了大部分噪声,去噪后的SET时频谱图可读性大大提高,且能清楚地看到滚动轴承故障特征频率集中的频段。 笔者再对去除噪声后的SET时频谱图进行重构,其结果如图10所示。 图10 重构的时域波形 与原始振动信号相比,重构的时域波形噪声明显减少,而且滚动轴承的故障冲击特征也得到了突出显示。 笔者对重构后的信号进行包络解调,得到其包络谱如图11所示。 图11 重构信号的包络谱 从图11中,可以清晰看到滚动轴承外圈故障频率的1~5倍频,从该包络谱中可以判断出滚动轴承外圈发生了故障。该结果也与滚动轴承外圈的实际情况相符。 笔者对原始振动信号进行包络解调。原始信号的包络谱如图12所示。 图12 原始信号的包络谱 从图12中,只能看到滚动轴承故障特征频率的1~3倍频。与图11相比,图12中的噪声较大,包含的故障特征频率信息较少。 下面,笔者再使用美国凯斯西储大学的故障轴承实验数据,来验证该方法的有效性。 滚动轴承故障模拟试验台如图13所示。 图13 故障模拟试验台 待检测的轴承支撑着电动机的转轴,在电动机驱动端的轴承座上方放置一个加速度传感器,用来采集故障轴承的振动加速度信号。其中,轴承型号为SKF6205,电机转速为1 796 r/min,采样频率为12 000 Hz。 故障轴承的具体参数如表2所示。 表2 故障轴承参数 本研究将使用上述轴承内圈故障的数据。内圈故障信号的时域波形如图14所示。 图14 时域波形 接下来的处理步骤和外圈故障处理步骤一样。SET处理的结果如图15所示。 图15 SET时频谱图 从图15中可以观察到:由于噪声较大,滚动轴承的故障信息完全被噪声所淹没,无法读取到有效的信息。 对图15进行SVD降噪,其结果如图16所示。 图16 基于SVD的SET时频谱图 由图16中可知:原来的噪声大部分被清除了,滚动轴承的故障信息清楚地显现出来,时频谱图的可读性也提高了。 笔者对去噪后的SET时频谱图进行重构,对重构后的信号进行包络解调,最后得到其包络谱,如图17所示。 图17 重构信号的包络谱 从图17中,可以清晰看到轴承的转频(fr)和轴承的故障特征频率及其倍频;并且从该包络谱中可以判断出滚动轴承的内圈已经发生了故障。该结果也与滚动轴承内圈的实际情况相符。 通过上述的对比分析可知: (1)基于SVD和SET的方法能有效去除原始振动信号中的噪声,得到清晰、整洁的时频谱图; (2)相比于单独进行的SET方法,基于SVD和SET的方法有明显的优势; (3)通过包络谱的对比,说明笔者提出的基于SVD和SET的方法应用于滚动轴承的故障诊断是有效的。 由于SET无法在时频谱图中清晰、准确地表达出滚动轴承的振动信号特征,为此,基于SVD在降噪方面的优势,笔者提出了一种SVD与SET相结合的滚动轴承故障诊断方法,即先采用SET方法对轴承振动信号进行同步提取变换,再利用SVD重构对其进行降噪处理,最后通过滚动轴承的外圈、内圈故障数据对该方法的有效性进行了验证。 研究结果表明: (1)相比于只进行SET处理的方法,SVD与SET相结合的方法具有很大的优势,即噪声明显减少,滚动轴承的故障冲击特征得到了突出显示; (2)采用SVD与SET相结合的方法,重构信号的包络谱上可以显示轴承的故障特征频率及其倍频,从而判断出滚动轴承是否发生了故障; (3)实际轴承信号的处理结果显示,SVD与SET相结合的方法是有效的,可以很好地应用于滚动轴承的故障诊断。 以上研究工作主要针对的是滚动轴承出现局部故障时,振动信号的处理以及故障诊断。SVD与SET相结合的方法在故障信号降噪和解调方面有优势,因此,在接下来的工作中,笔者会研究将方法应用于复杂装备滚动轴承的故障诊断,并且对该方法进行优化。2 基于SVD与SET的诊断方法
3 SVD与SET结合的优势


4 故障诊断试验
4.1 外圈故障分析



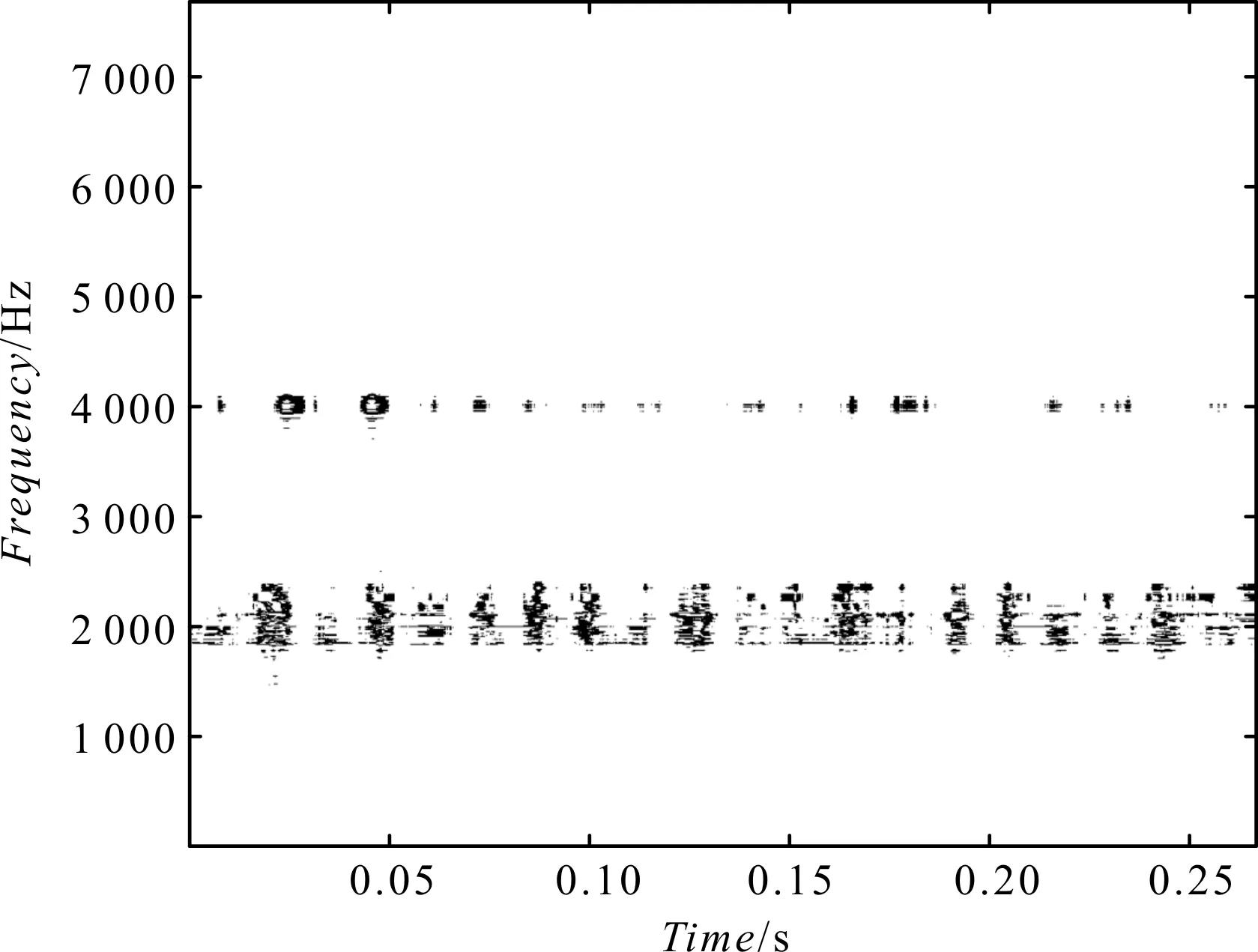

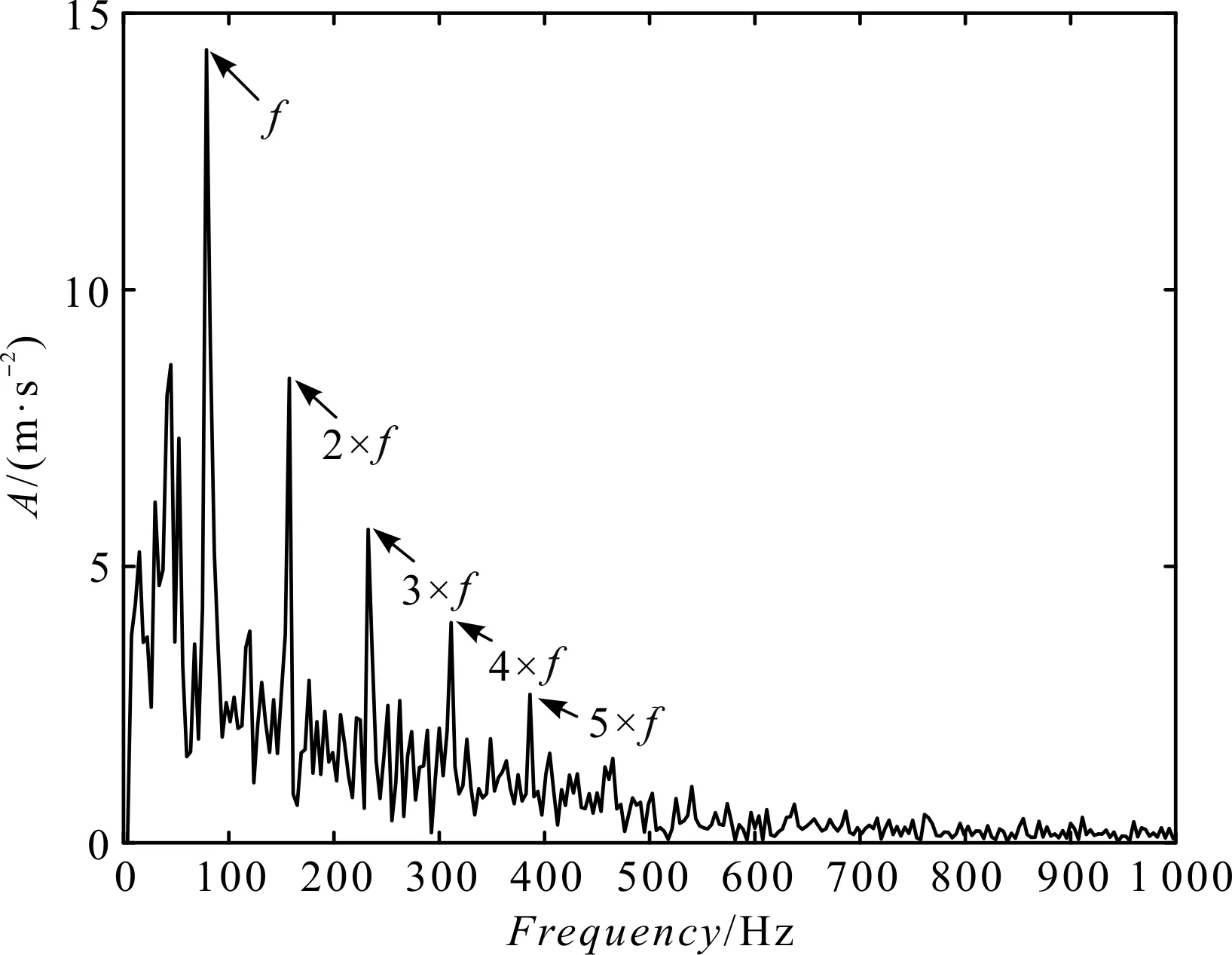
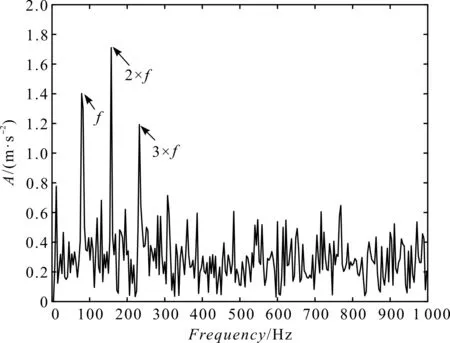
4.2 内圈故障分析



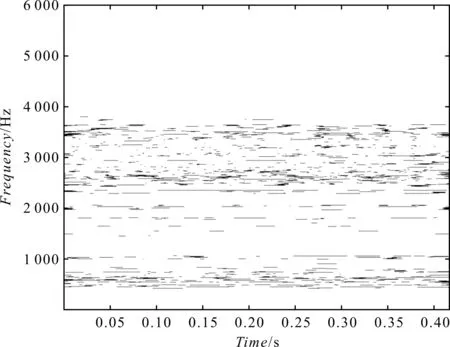
5 结束语

