基于CESGD和IMCCN的轴承故障识别研究*

沈为清,周正平,常兆庆

(1.江苏财经职业技术学院 智能工程技术学院,江苏 淮安 223003;2.南京航空航天大学自动化学院,江苏 南京 211106;3.江苏曙光光电有限公司,江苏 扬州 225000)

0 引 言

目前,滚动轴承已广泛应用于各类旋转机械设备中。因此,及时对滚动轴承进行状态监测具有重要意义[1]。

在工程实际中采集的轴承振动信号较易受到环境噪声的干扰,且表现出一定的非线性和非平稳性特征[2],导致传统的“特征提取—故障识别”的故障模式识别方法受到一定的限制[3]。

而采用卷积神经网络(convolution neural network,CNN)[4]时,它能自动从轴承振动信号中学习具有判别性的特征,从而可以克服传统故障识别方法的缺陷。但文献[5]指出,若直接将原始振动信号输入CNN中,信号的噪声会降低CNN的特征提取能力、故障识别能力,减缓其收敛速度。为了减弱噪声的干扰,彭鹏等人[6]将轴承振动信号堆叠转化成灰度图,然后将灰度图输入CNN中进行轴承故障识别,识别准确率达95%以上。胡茑庆等人[7]首先利用经验模态分解(empirical mode decomposition,EMD)方法对振动信号进行降噪,然后利用CNN进行自动特征提取与故障判别,最后得到的轴承故障识别准确率可以达到96%。

但上述研究中所使用的经验模态分解降噪方法存在模态混叠与端点效应等缺陷[8]。同时,直接将轴承的振动信号堆叠转化成灰度图的方法也存在较大的缺陷[9]。

辛几何分解(SGD)[10]是一种较为新颖的信号分解方法,它具有较为严格的数学基础,在故障诊断领域有一定的应用前景;但原始SGD分解结果的稳定性较低[11]。

在上述研究的基础上,笔者提出一种基于完备集成辛几何分解(CESGD)和改进多通道卷积网络(IMCCN)的滚动轴承故障识别方法。首先,对采集到的轴承振动信号进行CESGD分解;然后,进行集成平均并重构信号;最后,将重构信号输入IMCCN网络中,进行自动特征提取与故障识别。

1 CESGD信号降噪

1.1 SGD理论基础

由于SGD基于矩阵分解理论,它首先需要利用轴承振动信号x=x1,x2,…,xn来构造矩阵X。

矩阵X表达式如下:

(1)

式中:d—嵌入维度;τ—延迟时间。

其中：m=n-(d-1)。

进而得到协方差矩阵A:

A=XTX

(2)

然后,构造Hamilton矩阵M:

(3)

再根据Hamilton矩阵M构造辛正交矩阵Q:

(4)

式中:B—上三角矩阵;N—B的Schmidt正交化。

计算矩阵Q的特征值为λ1,λ2,λ3,…,λd,则矩阵A的特征值如下:

(5)

σ1>σ2>…>σd

(6)

σi的分布称为A的辛几何谱,Qi为对应于A特征值σi的特征向量。

令S=QTX,Z=QS,计算变换系数矩阵:

(7)

对Si进行变换,可得到Zi:

Zi=QiSi

(8)

则轨迹矩阵Z可以表示为:

Z=Z1+Z2+…+Zd

(9)

定义Zi中的元素为Zij,1≤i≤d,1≤j≤m,并且令:

(10)

则对角平均转换矩阵为:

(11)

通过对角平均将Z变换为d×n维的矩阵Y,从而可将信号x分解为d个具有不同趋势项和不同频带的SGMCs,即:

x=SGMC1+SGMC2+…+SGMCd

(12)

综上所述,SGD的算法步骤如图1所示。

图1 SGD算法步骤

1.2 CESGD理论

为了降低SGD的重构误差,并增强SGD分解结果的稳定性,笔者借鉴了完备集合经验模态分解的思想对信号进行处理,具体步骤如下:

(13)

(14)

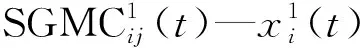
(3)重复步骤(1)、步骤(2);

(4)经N次循环得到2×N×k个SGMCs,并进行集成平均,即:

(15)

(5)根据集成均值和评价指标对信号进行重构,即:

(16)

评价指标Q的表达式如下:

Q=η1Kr+η2rxy+η3exy
0<η1、η2、η3<1
η1+η2+η3=1

(17)

式中:Kr—峭度;rxy—相关系数;exy—能量比。

各指标的权值选取参考文献[12]中的方法。

2 改进多通道卷积网络

实际工程中,大多使用多传感器系统对设备进行监测,以全面地反映机器的运行状态。由于传统的卷积神经网络对多传感器信号的行、列方向均进行卷积,但不同传感器振动信号是相互独立的,需要考虑不同传感器的不同组合[13]3。

因此,笔者提出一种改进多通道卷积网络(IMCCN),其结构如图2所示。

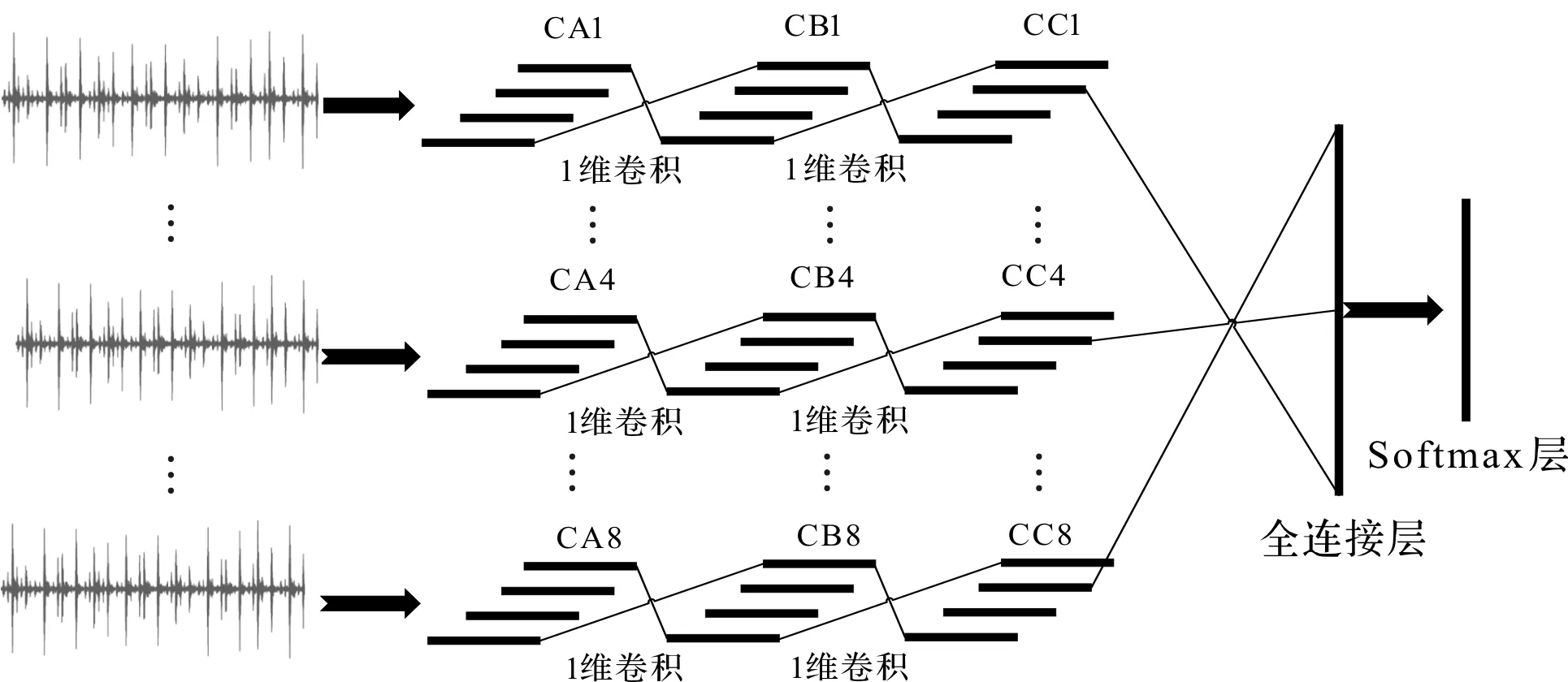
图2 IMCCN网络结构

每个传感器通道有3个卷积单元,笔者采用8个加速度传感器,共24个卷积单元;并选择Softmax层输出故障识别结果。

设输入x=[x1,x2,…,x8],xi(1≤i≤8)代表第i个通道的轴承振动信号,fc和fs分别代表卷积和池化操作。IMCCN的输出如下:

(18)

(19)

(20)

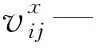
FD表达式如下:

FD(x)=φ(Wx+b)

(21)

式中:φ—ReLU激活函数。

FE表达式如下:

(22)

式中:K—故障类别数;Wj—权重;bj—偏置。

IMCCN的反向传播算法与CNN相同。

3 CESGD-IMCCN识别流程

基于CESGD-IMCCN的滚动轴承故障识别步骤如下:

(1)采集不同故障工况的滚动轴承振动信号样本;

(2)利用CESGD方法和评价指标对信号样本进行分解并重构,以达到降噪的效果;

(3)从重构样本中集中随机选取80%的样本作为训练集,其余作为测试集;

(4)初始化IMCCN参数;

(5)将训练集样本输入IMCCN中进行训练,通过反向传播算法调整网络参数;

(6)使用测试样本对训练好的IMCCN进行测试。

CESGD-IMCCN轴承故障识别流程图如图3所示。

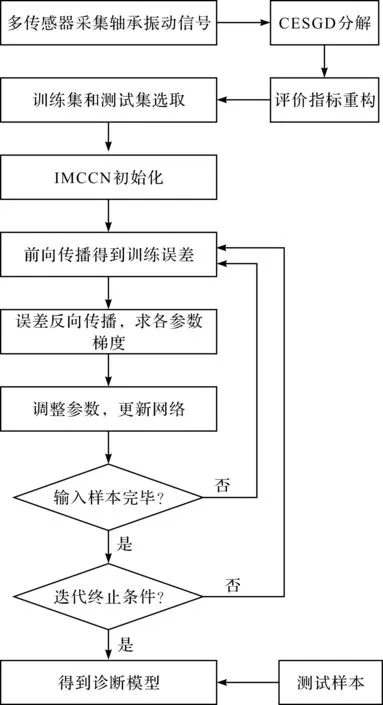
图3 CESGD-IMCCN轴承故障识别流程图

4 实验验证(基于实验室轴承数据)

4.1 轴承数据

为验证CESGD-IMCCN模型的可行性和有效性,笔者在轴承故障模拟实验台上进行测试。

该实验台由电动机、转速控制器、转轴等组成,如图4所示。

图4 轴承故障模拟实验台

此处所使用的8个传感器分别安装在实验台驱动端和风扇端等位置。滚动轴承测试型号为SKF6205。实验前,笔者通过电火花加工方式,在滚动轴承上加工出不同故障尺度的凹槽(轻微故障0.18 mm、中度故障0.36 mm和重度故障0.51 mm)。采样频率为12 000 Hz。工况设置参照文献[14]。

笔者选取了10种轴承运行工况如表1所示(转速均为1 748 r/min)。

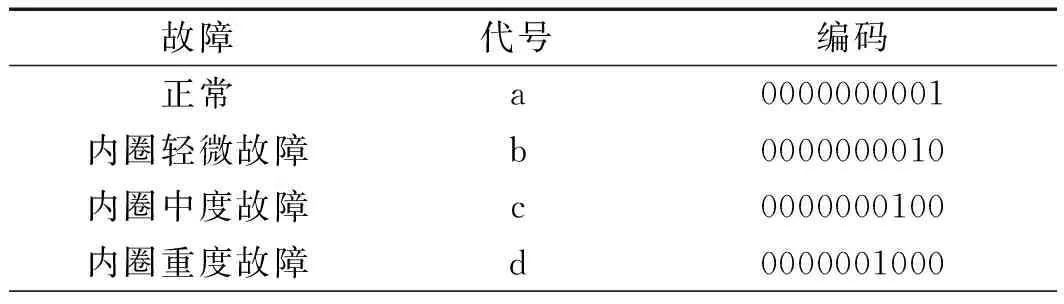
表1 轴承10种运行工况

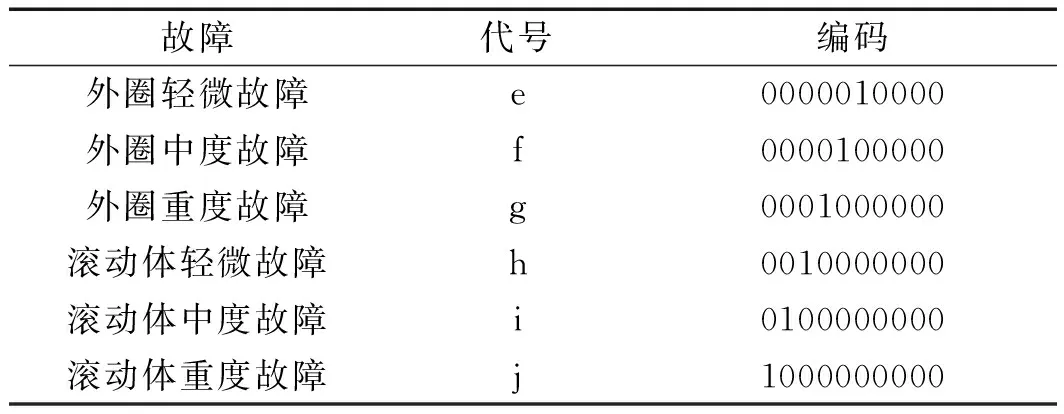
续表

表1中,每种工况下的样本各8 000个,每个样本2 048个采样数据点。

10种运行工况下轴承时域图如图5所示。

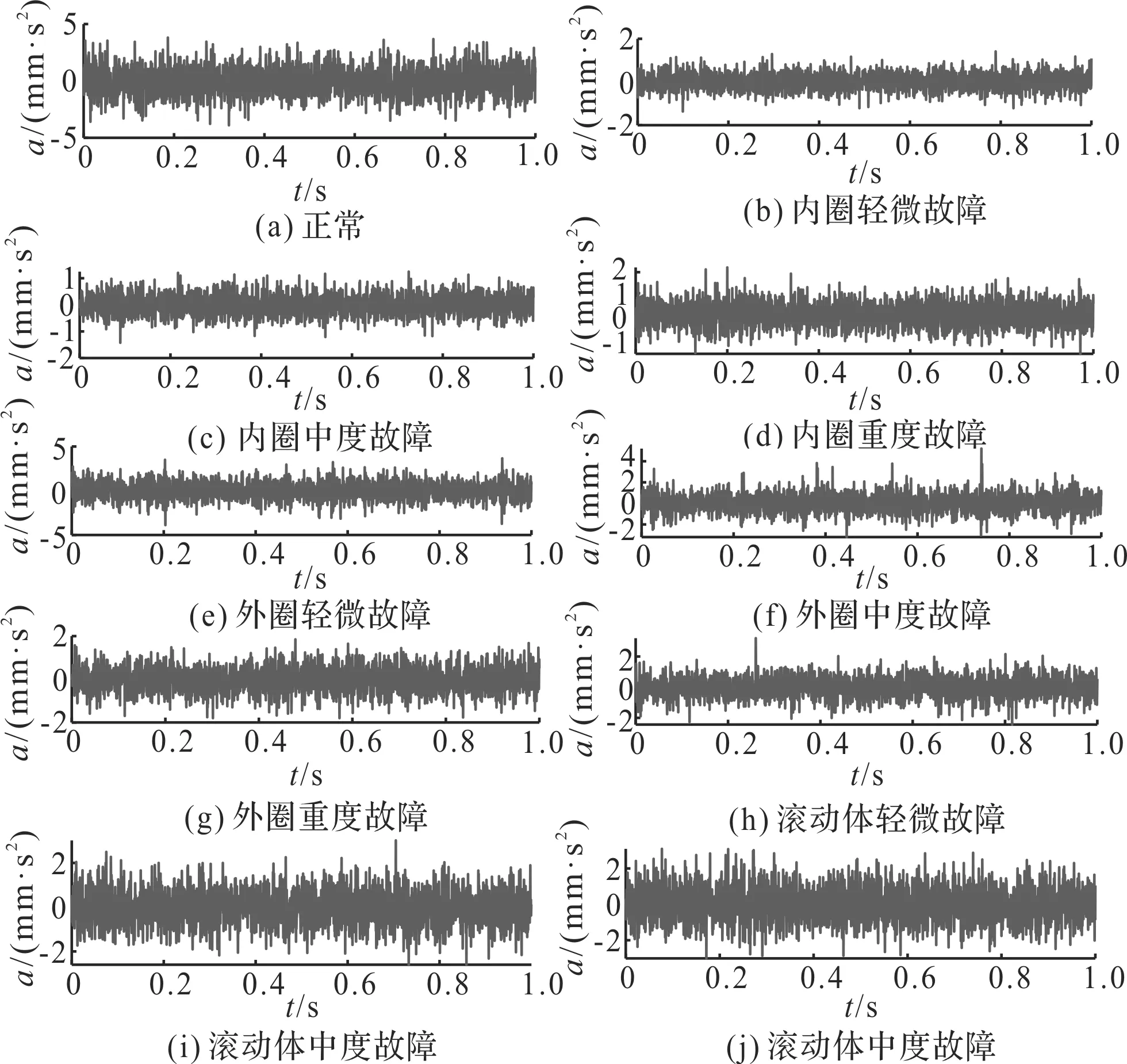
图5 轴承10种运行工况时域波形图

由图5可知：信号受噪声干扰严重,难以对滚动轴承的运行故障工况直接进行有效区分。

4.2 信号分解对比

此处以滚动体轻微故障工况下振动信号为例(工况h),经计算得到滚动体故障频率约为141.1 Hz,转频约29.2 Hz。

笔者采用原始SGD和CESGD对其进行分解。其中,原始SGD分解结果如图6所示。

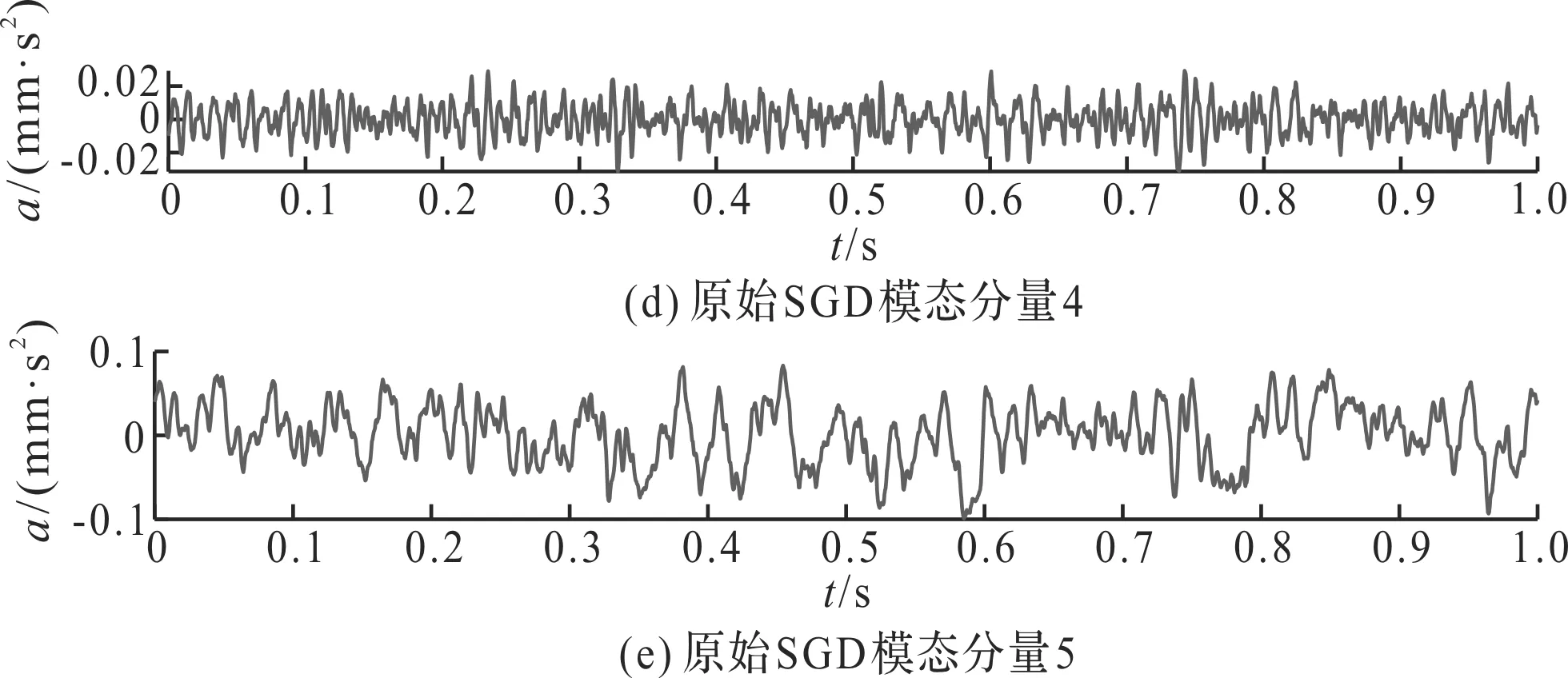
图6 原始SGD分解结果

CESGD分解结果如图7所示。

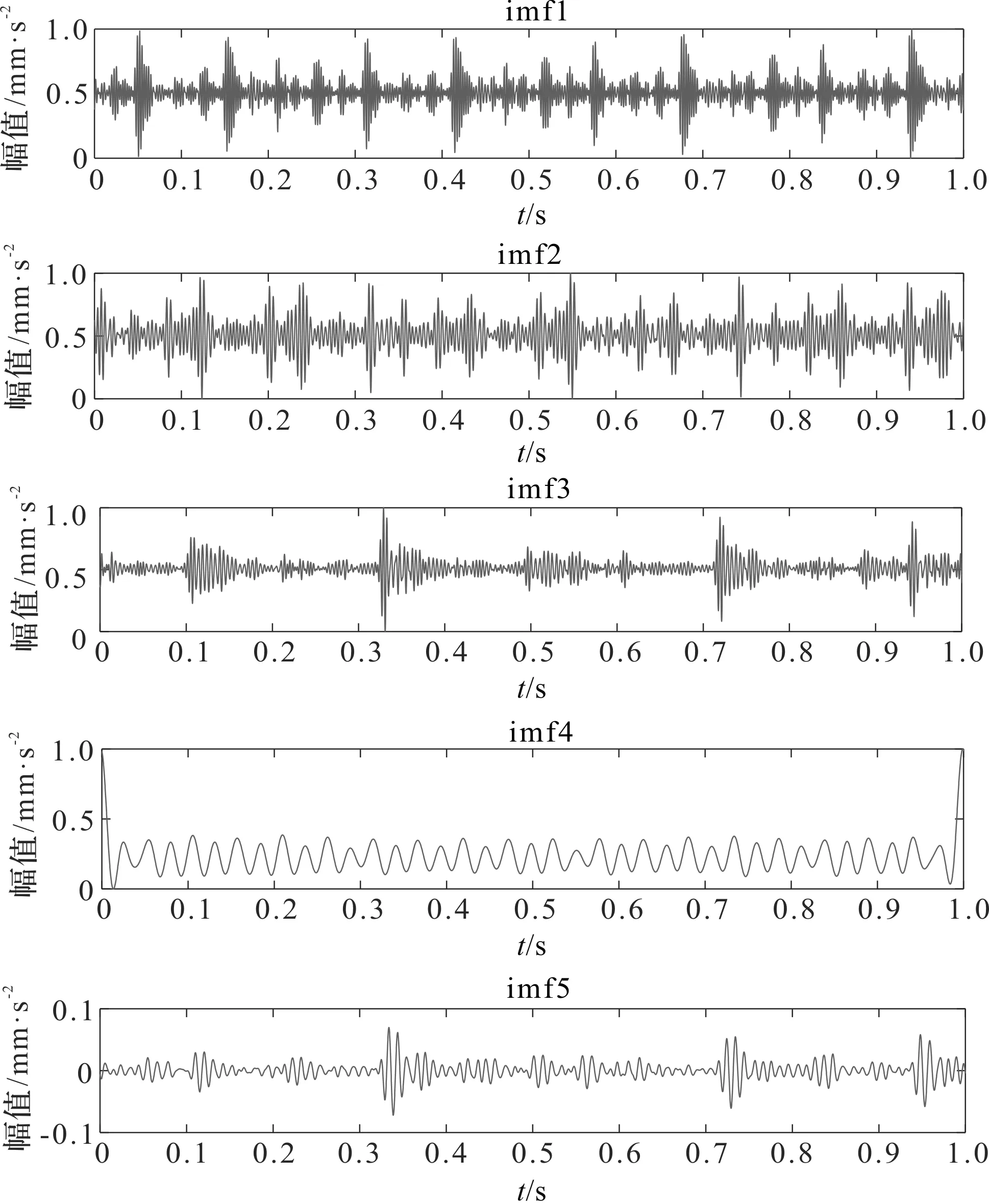
图7 CESGD分解结果

笔者根据评价指标对分解信号进行重构。其中,原始SGD分解重构后的功率谱如图8所示。

图8 原始SGD分解重构信号功率谱

CESGD分解重构后的功率谱如图9所示。

图9 CESGD分解重构信号功率谱

相较于图8,从图9可以明显看出:转频的四分之一倍频5.8 Hz,故障频率140.6 Hz及其2倍频281.3 Hz;该结果验证了CESGD的优越性。

4.3 与其他信号前处理对比分析

笔者采用不同的信号分解方法(CEEMD、EMD、变分模态分解VMD、原始SGD和CESGD)进行对比分析。

经10次实验,采用不同信号分解方法的结果如表2所示。

表2 不同信号分解方法的识别结果

由表2可知:

(1)相较于其他方法,基于CESGD信号分解方法的故障识别率更高,也更稳定;(2)EMD方法由于模态混叠严重,无法进一步给IMCCN提供优秀的训练样本,导致轴承故障识别率较低,仅92%左右;(3)CEEMD和VMD在一定程度上缓解了模态混叠缺陷,其识别效果优于EMD;(4)SGD基于辛几何分析,在分解过程中能有效避免信号发生畸变,相比于VMD和CEEMD,SGD能较准确地分解轴承振动信号;(5)CESGD借鉴了CEEMD的思想,在轴承振动信号中添加符号相反且幅值相等的正负白噪声对,有效地增强了SGD分解结果的稳定性。

4.4 与单传感器的故障识别准确率对比

为验证多传感器的优势,笔者参考了文献[13]5-6中所用的对比方法,将每个通道的信号以相同的方式输入模型,作为1种方法,共8种方法(8个传感器通道,即方法1～方法8)。

经10次实验,不同传感器通道的平均故障诊断准确率如表3所示。

表3 与单传感器故障识别效果对比

表3实验结果表明:单传感器的平均准确率最高为90.13%,最低为85.98%,均低于本文方法;该结果验证了多传感器故障识别的优越性。

4.5 噪声对模型故障识别准确率的影响

笔者通过添加不同信噪比(SNR)的噪声进行对比实验;设置了20 dB、10 dB、5 dB的实验,相应的对比结果如表4所示。

表4 不同噪声下不同方法的对比结果

由表4可知:随信噪比的降低,不同方法的故障识别准确率均有所降低;

但相比于其他方法,CESGD-IMCCN方法的识别率更高,这是因为CESGD在轴承振动信号中添加符号相反且幅值相等的正负白噪声对,有效增强了SGD分解结果的稳定性。

5 实验验证(基于CWRU轴承数据)

为验证CESGD-IMCCN模型的可行性和有效性,笔者再次使用CWRU(美国凯斯西储大学)轴承公开数据集[15]进行测试。

美国凯斯西储大学实验台如图10所示。

图10 CWRU实验台

笔者取CWRU数据集中采样频率12 000 Hz的信号样本;4种工况状态为:内圈故障、外圈故障、滚动体故障以及正常状态;每种故障损失直径分别为0.18 mm、0.36 mm和0.54 mm。

最后,笔者取每种工况下样本各8 000个,每个样本2 048个采样数据点。

CWRU数据集10种工况设置如表5所示。

表5 CWRU数据集10种运行工况

续表

首先,笔者采用4种信号分解方法(EMD、VMD、原始SGD和CESGD)进行对比分析。

经10次实验,4种信号分解方法的平均故障识别结果如表6所示。

表6 4种信号分解方法的平均故障识别结果

由表6可知:相较于其他方法,基于CESGD信号分解方法的故障识别率更高,也更稳定;该结果进一步验证了CESGD前处理的有效性。

其次,笔者采用几种新的深层模型进行对比分析,新模型分别为:文献[16]中的堆栈收缩自编码网络(SCAE)、文献[17]中的深度脊波卷积自编码网络(DRCAN)和文献[18]中的门控循环单元胶囊网络(CNGRU)。

经10次实验,不同深层模型的平均故障识别结果如表7所示。

表7 不同深层模型的平均故障识别结果

由表7可知:相比于SCAE、DRCAN和CNGRU深层模型,IMCCN的故障识别率和稳定性都较高,SCAE、DRCAN和CNGRU 3种深层模型的识别率相差无几;该结果表明,IMCCN模型的通用性较好,同时也进一步验证了IMCCN模型的优越性。

6 结束语

针对传统滚动轴承故障识别算法存在的特征提取与特征选择困难的问题,笔者提出了一种基于CESGD-IMCCN的滚动轴承故障识别方法。首先,利用CESGD对滚动轴承多传感器振动信号进行分解;然后,利用评价指标选择合适的模态分量并进行了重构,再将重构降噪振动信号输入IMCCN进行自动特征提取与故障识别;最后,采用轴承故障模拟实验台轴承数据集和美国凯斯西储大学轴承公开数据集分别进行了实验,验证了CESGD-IMCCN模型具有较好的故障识别效果。

主要结论如下:

(1)提出的CESGD借鉴了完备集合经验模态分解的思想,在信号中添加白噪声对,然后利用SGD将信号分解,对噪声具有较强的鲁棒性,分解结果较为稳定;

(2)将IMCCN用于轴承故障诊断,不同通道数据使用不同的卷积核,更有利于轴承振动信号的特征提取与故障诊断。

在之后的工作中,笔者将进一步研究如何利用SGD对滚动轴承故障信号进行更有效的分解;同时,研究IMCCN更有效的优化方法。