基于CEEMD散布熵和Hjorth参数的混合特征滚动轴承故障诊断研究*
夏理健,刘小平,王 新,田 笑,张立杰
(1.燕山大学 河北省重型机械流体动力传输与控制重点实验室,河北 秦皇岛 066004;2.北京航空航天大学 自动化科学与电气工程学院,北京 100191;3.燕山大学 先进锻压成形技术与科学教育部重点实验室,河北 秦皇岛 066004)
0 引 言
由于滚动轴承经常在重载、冲击和变载荷等复杂工况条件下工作,其故障的发生率极高。滚动轴承发生故障时,会严重影响机械设备的正常运行,甚至会引发安全事故[1]。因此,对滚动轴承进行状态检测和故障诊断,对机械设备的安全运行具有重要意义。
当滚动轴承发生局部故障时,其振动信号通常呈现出非线性和非平稳性的特征。早期的脉冲信号非常微弱,易受到强环境噪声影响,导致故障特征难以提取。因此,有必要通过信号分解的方式来提取其故障特征。
采用经验模态分解(empirical mode decomposition,EMD)及其改进算法获取振动信号特征的方法是当前的热点研究方向之一。刘永强等人[2]利用集合经验模态分解(ensemble empirical mode decomposition,EEMD)和自相关函数峰态系数,对轴承进行了故障诊断,但每次EEMD分解需要加入不同幅值的白噪声,使各个固有模态分量(IMF)中有残留噪声,影响了序列中的有效信息提取,导致其分解精度不高。TORRES M E等人[3]提出了一种完备总体经验模态分解(CEEMD)方法,采用该方法可以减小由白噪声导致的重构信号误差,更好地抑制模态混叠现象,提高分解精度。
熵是分析信号动态变化的有力工具,可以反映信号的混乱程度。信息熵能够有效地检测故障振动信号的动力学突变,因此,利用熵能够反映信号复杂程度的特性,可以达到提取特征信息的目的。其中,排列熵(permutation entropy,PE)应用较为广泛。
陈祥龙等人[4]提出了一种采用改进排列熵,来表示滚动轴承振动信号特征的方法。石志炜等人[5]先用CEEMD分解滚动轴承的振动信号,然后求解IMF分量的排列熵,从而得到了其特征向量。虽然PE计算简单,但其没有考虑幅值之间的大小关系。2016年,ROSTAGHI M等人[6]610-611提出了一种新的信号不规则程度指标—散布熵(DE)。DE算法的速度很快,且考虑了幅值间的关系,具有更好的抗噪能力。李从志等人[7]采用了一种将EMD与DE相结合的方法,实现了对滚动轴承的故障诊断。
由于单一方面的特征只包含部分信息,利用多个物理特征进行混合特征提取可以全面体现故障特征信息,有利于提取更广泛的故障特征信息。
Hjorth参数最早由HJORTH B[8]提出,目前已被广泛应用于脑电信号的特征提取和分析处理。Hjorth参数是一种可以同时描述振动信号在时域、频域中瞬时特征的统计函数。CAESARENDRA W等人[9]在对低速回转轴承状态进行监测的研究中,应用3个Hjorth参数,但在轴承状态监测中的应用效果并不理想。GROVER C等人[10]将EMD与Hjorth参数结合起来,以计算相关性最高的IMF的Hjorth参数作为特征向量,来对滚动轴承进行故障诊断,取得了不错的效果。
但是,只选用相关性最高的IMF来进行计算,必然会丢掉部分故障信号的信息。因此,该方法还有待于进一步改进。
基于上述问题,笔者提出一种基于CEEMD的散布熵与Hjorth参数的混合特征故障诊断方法。首先,对滚动轴承信号进行CEEMD分解,得到若干个IMF分量,并计算各个分量与原始信号的相关性,选取相关性较高的前几个IMF分量;然后,求所选IMF的散布熵和Hjorth参数,形成散布熵特征向量和Hjorth参数矩阵,对Hjorth参数矩阵进行奇异值分解(SVD),利用奇异值向量与散布熵特征向量形成混合特征向量来代表滚动轴承振动信号;最后,利用基于粒子群优化算法(PSO)优化的最小二乘支持向量机(LSSVM),对滚动轴承不同故障特征向量进行训练和识别,利用滚动轴承不同故障试验数据对所提方法进行验证。
1 基本理论和方法
1.1 CEEMD算法理论
由于EMD算法是从原信号中提取若干个固有模态分量IMF,每一阶IMF都反映原始信号的动态特性。但一些有异常干扰的非线性信号会产生模态混叠,导致多个模拟主导频率分量同时出现在一个模态分量中。
EEMD将白噪声加入到原始信号当中,利用白噪声频谱的均匀分布,使不同时间尺度的信号自动分布到合适的参考尺度上,可有效抑制模态混叠;但添加的白噪声会使IMF分量在重构时产生误差。
为了解决白噪声的干扰,且在重构信号时产生误差的问题,通常采用CEEMD算法,通过给原始信号添加符号相反的白噪声,分别对两组信号进行EMD分解,使重构误差明显减小,添加的白噪声得到中和。
CEEMD分解的具体过程如下:
(1)初始化添加辅助白噪声的次数n和白噪声幅值k,令i=1;
(2)将第i次添加白噪声的信号进行EMD分解。在原信号中以正负成对的形式加入辅助白噪声,从而得到信号:
(1)
式中:x(t)—原始信号;ni(t)—第i次添加的辅助噪声;Pi(t)—加入正噪声后的信号;Ni(t)—加入负噪声后的信号;n—信号个数。
对加入白噪声后的信号Pi(t)和Ni(t)进行EMD分解,使每个信号得到q个IMF分量,即:
(2)
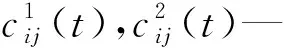
其中:j=1,2,…,q。
(3)如果i (3) 式中:cj(t)—信号经CEEMD分解后得到的第j个IMF分量;r(t)—最终残余分量。 该方法保证了信号分解的完备性,可以较好地解决模态混叠效应问题。需要注意的是,添加高斯白噪声的次数n一般取100~300[11],此时噪声残留所引起的误差非常小。 白噪声幅值k的值通常取为原始信号标准差的0.2~0.5倍,取值也可随噪声的强度而适当调整增大[12]。此处所使用的n取100,k取0.2σx(σx为原始信号的标准差)。 散布熵算法是一种用来度量时间序列复杂性和不规则程度的新算法。散步熵对同步频率、振幅值和时间序列带宽的变化很敏感,而且受突变信号影响较小,具有更好的抗噪能力,因此,它比排列熵的计算效率更高。 对于时间序列x={xj,j=1,2,…,N},散布熵的计算步骤如下: (1)利用正态累计分布函数,将x映射为y={yj,j=1,2,…,N},yj∈(0,1),其正态分布函数为: (4) 式中:μ—时间序列x的期望;σ—时间序列x的标准差。 (2)通过线性变换把y映射到[1,2,…,c]范围,即: (5) (6) 式中:m—嵌入维数;d—时延。 (5)计算每种散布模式πv0v1…vm-1的概率p(πv0v1…vm-1): (7) (6)根据香农熵的定义,对于嵌入维数为m、时间延迟为d以及类别数为c的原始时间序列x,其归一化的散布熵可表示为: (8) 散布熵与信号的不规则程度相关,DE值越大,信号不规则程度越高,反之越低。 在参数选择方面,文献[6]611建议m通常取2或3,c取[4,8]间的整数,时间序列长度大于2 000。时延d的值大于1可能会造成信息的丢失,故笔者取m=3,c=6,d=1,每段时间序列长度为2 048。 Hjorth参数是为计算时变信号的平均功率、均方根频率以及均方根频率展开等信号特征时,提供的一种方法。使用Hjorth参数进行计算时,由于涉及方差,使得其计算成本非常低。 3个Hjorth参数分别称为:活动性(Activity)、移动性(Mobility)和复杂性(Complexity)。 活动性定义为信号的方差,表示信号的幅度特性,其公式如下: Activity=σ2 (9) 式中:σ—信号的标准差。 移动性定义为信号的一阶差分信号的方差和信号自身方差之比的均方根。具体公式如下: (10) 式中:σ′—原始信号的一阶差分信号的标准差。 复杂性定义为振动信号一阶导数的迁移率与振动信号的迁移率之比。它给出了信号带宽的估计值,表明振动信号与纯正弦波的相似程度。其公式如下: (11) 式中:σ″—原始信号二阶差分的标准差。 基于CEEMD散布熵和Hjorth参数的混合特征提取步骤为: (1)对采集到的信号用CEEMD进行分解,得到若干个IMF分量。 (2)为了尽可能提取有用的特征信息,并去除虚假信息,需要对虚假的IMF分量进行剔除;通过计算所有IMF分量与原信号的相关性系数Cr,筛选出相关系数较大的前m个IMF分量,来代表原信号中的有效信息。 相关系数Cr的计算公式如下: (12) (3)计算筛选出的m个IMF分量的散布熵,并构成散布熵特征向量E: (13) (4)计算筛选出的m个IMF分量的Hjorth参数,并构成Hjorth参数矩阵H: (14) 式中:Ai,Mi,Ci(i=1,2,…,m)—第i个IMF分量的活动性、移动性和复杂性。 (5)为了把H矩阵中的信息和散布熵特征向量E中的信息拼接成混合特征向量,必须把H矩阵中的信息转化成向量的形式。奇异值往往对应着矩阵中隐含的重要信息,且重要性和奇异值大小正相关。奇异值由于具有稳定性及比例不变性等良好性质,常被用来作为矩阵固有特征[13]。 故此处对H矩阵进行奇异值分解,提取分解后的奇异值向量Sv。SVD的具体公式如下: (15) 式中:S=diag(θ1,θ2,…,θq)—奇异值组成的对角阵,θ1≥θ2≥…≥θq,θi(i=1,2,…,q)—H矩阵的奇异值;U,V—左右正交矩阵;ui—矩阵U的第i列;vi—矩阵V的第i列。 其中:q=min(m,3)。 把S对角阵转化成能够代表H矩阵的奇异值特征向量Sv: (16) (6)把散布熵特征向量E和奇异值特征向量Sv拼接起来,构成能够代表原信号信息特征的混合特征向量F: F=[ESv]=[e1e2…emθ1θ2…θq] (17) 该方法从多个方面提取信号的特征,得到的信息更加全面,能够更好地突出不同信号之间的不同特征信息。 LSSVM是在原有支持向量机基础上的一种改进算法,在解决小样本故障数据、非线性问题时具有很大优势。LSSVM的具体算法如下: 设给定的训练样本{(x1,y1),(x2,y2),…,(xn,yn)},其中,xi为输入样本,yi为输出标签。 线性决策函数构造如下: f(xi)=ωTφ(xi)+β (18) 式中:ω—权重向量;β—偏差量;φ(·)—核函数。 按照结构最小化原理,可把LSSVM的优化问题转化为以下表达式: (19) 式中:ei—样本的拟合误差;γ—正则化参数。 为了解决上述问题,笔者构建拉格朗日函数: (20) 式中:λi—拉格朗日算子。 其最优化条件为: (21) 消去参数ei和ω,经整理可得线性方程组: (22) 式中:矩阵Ω=yiyjφT(xi)φ(xj)=yiyjK(xi,xj);K(·)—高斯核函数;yT—标签矩阵;I—单位矩阵。 最后,LSSVM的决策函数为: (23) LSSVM将最优化问题转换成线性方程组问题,提高了其运算速度。 基于CEEMD的散布熵和Hjorth参数的混合特征故障诊断方法主要包括3个阶段:故障特征提取、故障分类模型构建和故障诊断。 具体3个阶段如下: (1)利用CEEMD分解原信号,筛选出相关性高的IMF,计算其散布熵特征和Hjorth参数特征,形成混合特征向量,构建初始特征集; (2)将初始特征集划分为训练集和测试集两部分,利用训练集样本训练最小二乘支持向量机分类器,构建PSO-LSSVM模型; (3)利用PSO-LSSVM模型对测试集样本进行故障诊断,识别故障类型。 滚动轴承故障诊断方法的流程图如图1所示。 图1 滚动轴承故障诊断方法流程 此处实验采用的是美国凯斯西储大学电气工程实验室的滚动轴承数据[14]。该数据是使用安装在驱动端型号为SKF6205-2RS的深沟球轴承上采集得到的。 实验轴承数据信息如下:采样频率12 kHz,电机转速1 730 r/min;故障轴承采用电火花加工出单点损伤,滚动体、内圈和外圈的故障直径各取3种,外圈滚道的故障在6点钟位置。 正常信号和不同故障程度的故障信号共10种,每种数据取50个样本,共500个样本。其中,训练集的样本数为400,测试集的样本数为100,样本长度为2 048。 数据集的故障类别描述如表1所示。 表1 滚动轴承10种故障类别的数据集状态 滚动轴承的振动信号中,每种状态典型样本的振动图像如图2所示(其中,横轴代表采样点1~2 048,纵轴表示幅值)。 图2 滚动轴承的振动信号 首先,在10种状态下,各样本信号先经CEEMD分解得到各个IMF分量,然后计算出与各自原始信号相关系数的平均值,如图3所示。 图3 10种状态各个IMF分量与原信号的相关系数 图3中,几乎所有前3个IMF分量与原始信号的相关系数都在0.1以上,说明前3个IMF分量与原始信号相关性较强,涵盖了信号中的主要故障信息。 综上所述,笔者选取前3个IMF分量,分别计算其散布熵和Hjorth参数,并对Hjorth参数矩阵奇异值进行分解,把得到的三维奇异值向量和三维散布熵特征向量拼接成混合特征向量,共可得到10个特征集,从而完成对滚动轴承的特征提取。 为了说明DE算法的优越性,笔者将DE与PE进行对比,即采用两种算法,分别计算信号的前3个IMF分量的熵值;然后以IMF1的熵值为横坐标值,以IMF2的熵值为纵坐标值,以IMF3的熵值为竖坐标值,绘制成特征散点分布图。 其中,3D散布熵特征散点分布图如图4所示。 图4 3D散布熵特征散点分布图 3D排列熵特征散点分布图如图5所示。 图5 3D排列熵特征散点分布图 从图4和图5中的坐标跨度可以看出:不同故障类别DE特征之间的类别距离相对较大,在不同故障之间有更好的区分度;而不同故障类别的PE特征之间聚集现象更明显,只有正常信号与所有故障之间的区分较大。 为了验证Hjorth参数矩阵奇异值分解形成的奇异值特征向量与故障之间的相关性,笔者计算了每个奇异值特征与故障标签之间的最大信息系数。 最大信息系数[15]是用来捕捉每个特征与标签之间的任意关系(包括线性和非线性关系)的过滤方法,它返回每个特征与目标之间的互信息量的估计量,这个估计量的取值在[0,1]之间(其中,0表示2个变量独立,1表示2个变量完全相关)。3个奇异值特征与故障标签之间的最大信息系数分别为0.919 6、0.741 8、0.958 0,均大于0.5,说明Hjorth参数和故障之间有很好的相关性。 为进一步验证3个奇异值与故障之间的相关性,笔者分别使用1~3个奇异值特征进行故障诊断,其识别准确率如表2所示。 表2 基于不同数量奇异值特征的准确率 从表2中可以看出:使用奇异值在1~3个特征数量,其识别准确率单调递增,说明每个奇异值特征都与故障信息相关。 在不同故障状态下,滚动轴承的三维奇异值特征散点图,如图6所示。 图6 3D奇异值特征散点分布图 由图6可知:不同故障状态下,特征的分布有明显的差异,而且坐标跨度比三维PE特征散点图大,故可以说明,将奇异值序列作为特征向量,可以较为明显地区分开不同的故障状态。 笔者将每种故障混合特征样本数据随机打乱,分成400个训练集和100个测试集,用训练集训练PSO-LSSVM模型,用测试集来进行验证。为了使诊断结果可视化,笔者采用混淆矩阵来表现每一类故障的分类情况,并利用精确度P和召回率R[16]对其进行评估。 在故障测试集上,滚动轴承的分类结果如图7所示(分类错误的个数为0,即所有故障状态的精确度和召回率都是100%)。 图7 轴承测试样本分类归一化混淆矩阵 从以上分析中可知,基于散布熵和Hjorth参数的混合特征能够较好地反映不同的故障状态。 为了对基于散布熵和Hjorth参数(表示的是Hjorth参数矩阵分解的奇异值向量)的混合特征方法在故障分类方面的优势进行评估,笔者将该方法与只用单一排列熵、散布熵和Hjorth参数矩阵奇异值特征方法进行比较,并将其与基于排列熵和Hjorth参数的混合特征进行比较,结果如表3所示。 表3 不同方法的诊断结果 由表3可以看出: 基于CEEMD散布熵和Hjorth参数的混合特征方法的诊断准确率最高,达到了100%,利用排列熵和Hjorth参数矩阵奇异值的混合特征方法的准确率略低;同时,利用单一特征的诊断准确率均低于利用混合特征的准确率,证明了CEEMD相对于EEMD算法的优越性;笔者提出的Hjorth参数矩阵特征提取算法,在不同的信号分解算法中都保持了较高的准确率,受到的影响也较小。 以上分析结果充分验证了笔者采用的混合特征在轴承故障诊断中的有效性和准确性。 笔者提出了一种基于CEEMD散布熵和Hjorth参数的混合特征滚动轴承故障诊断方法;首先提取出了故障轴承振动信号多个物理方面的特征信息,然后构建起了PSO-LSSVM故障诊断模型,实现了对滚动轴承的故障诊断,最后通过实验验证了该混合特征提取方法在对滚动轴承多状态故障进行诊断时的可行性和优越性。 研究结果表明: (1)利用CEEMD算法和相关系数法提取敏感IMF,可以提取出与故障信息相关的IMF,解决EMD分解中的模态混叠问题; (2)把振动信号的散布熵和Hjorth参数混合特征用于故障诊断,能够从多个维度反映轴承故障的特征,解决单一物理特征诊断精度低的问题; (3)对比分析结果表明,该方法的诊断结果优于基于单一特征的故障诊断方法。 在今后的研究中,笔者将在考虑更多影响模型的因素的基础上,针对支持向量机进行更深入的理论研究。同时,由于粒子群优化算法的初始参数设置基于个人经验,不同初始参数是否会影响故障的识别效果,还有待于笔者做进一步的研究。1.2 散布熵算法

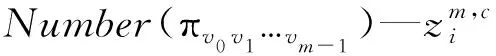
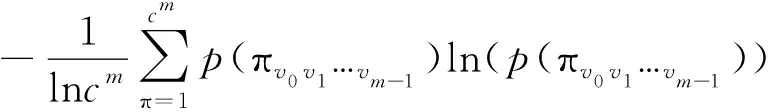
1.3 Hjorth参数
2 基于CEEMD的混合特征提取
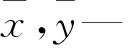

3 基于PSO-LSSVM的轴承故障诊断
3.1 最小二乘支持向量机模型
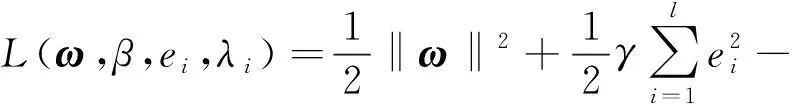
3.2 整体流程
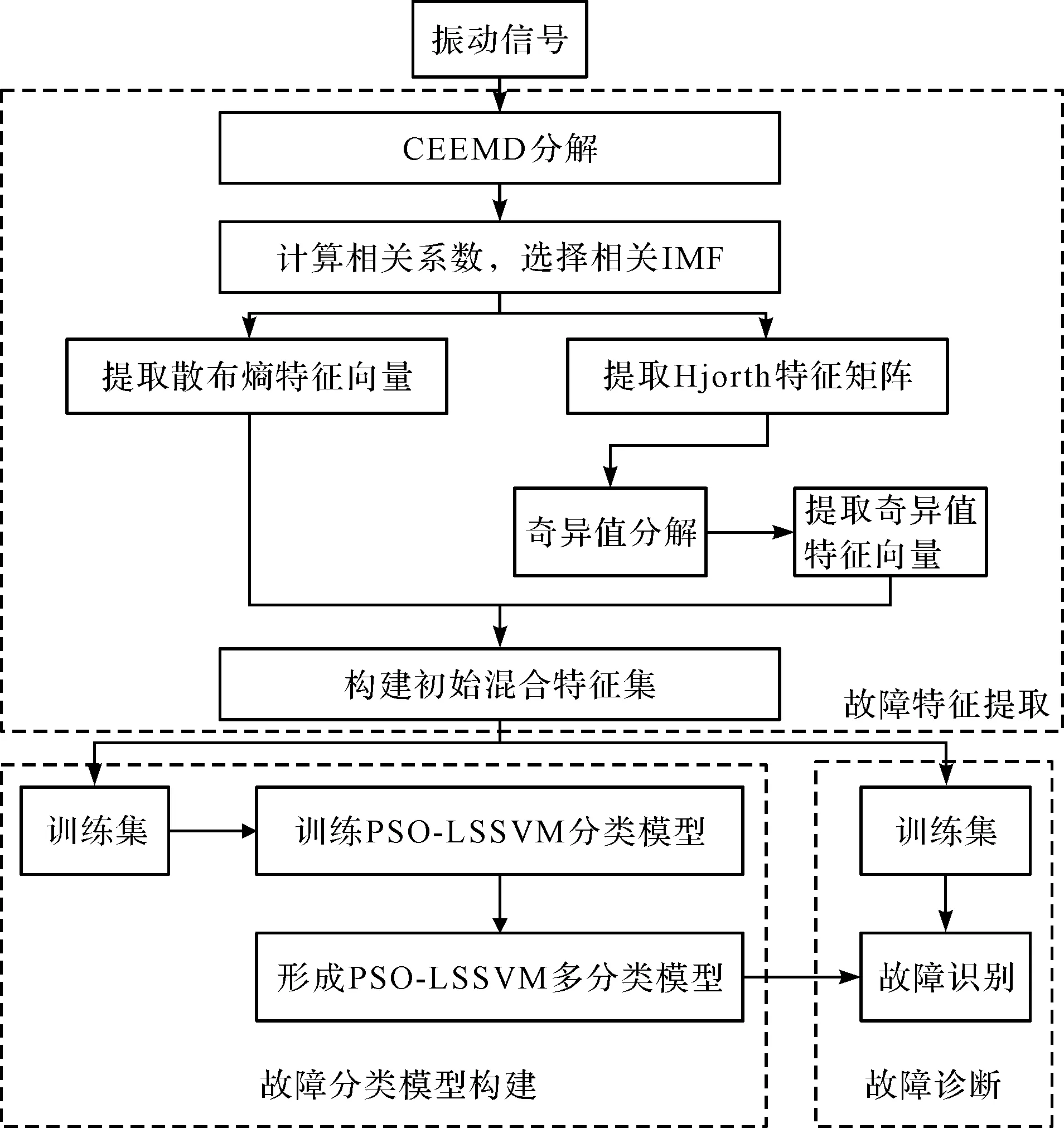
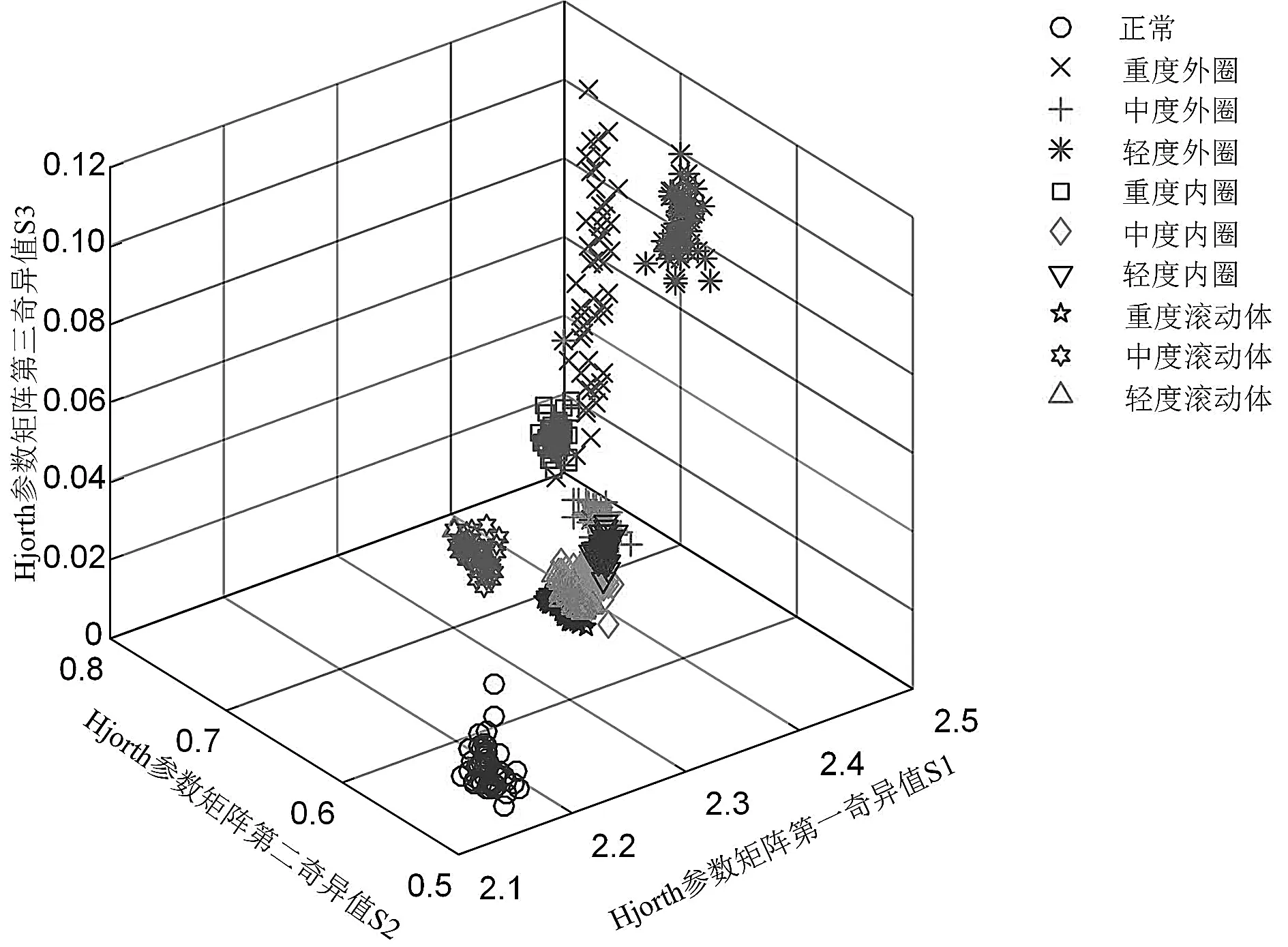
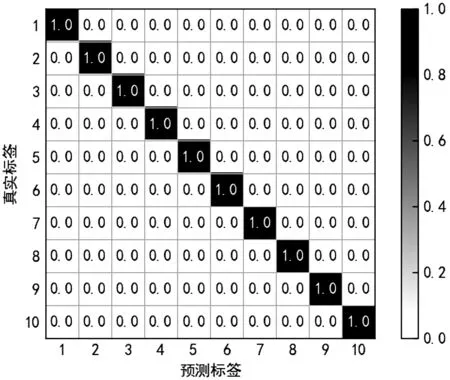
4 实验与结果分析
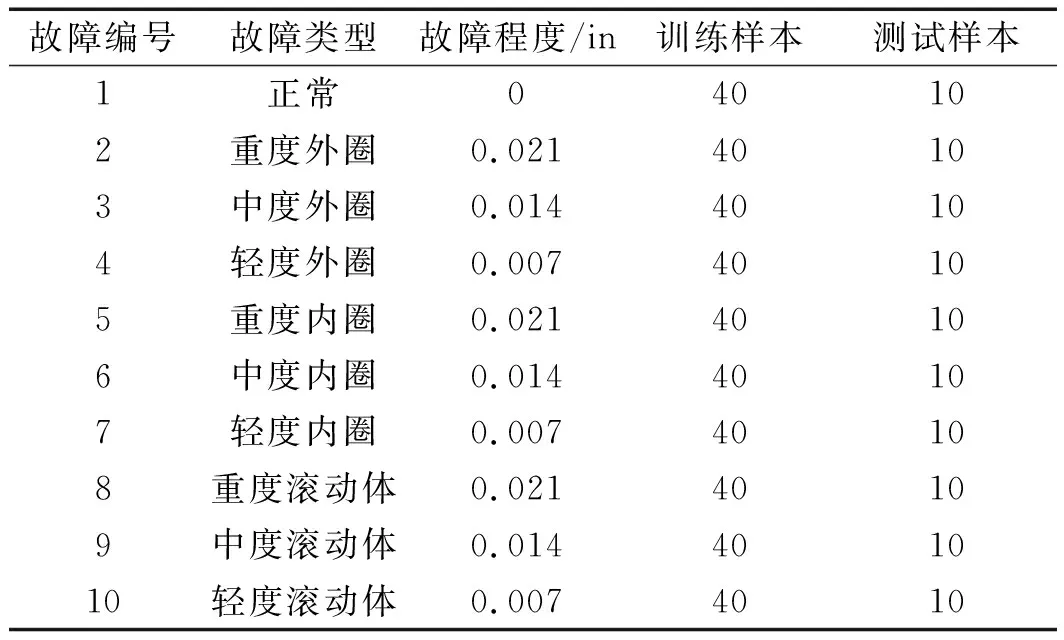
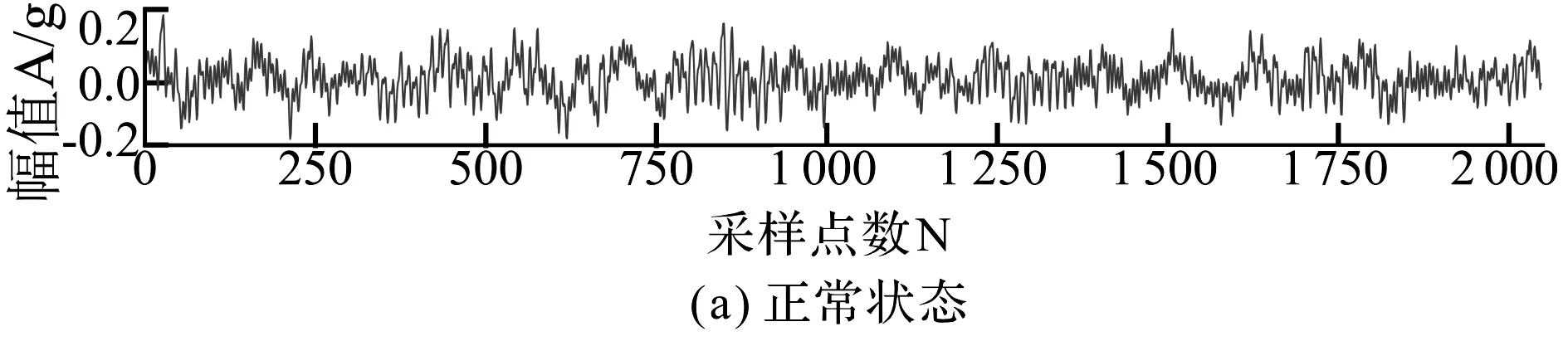
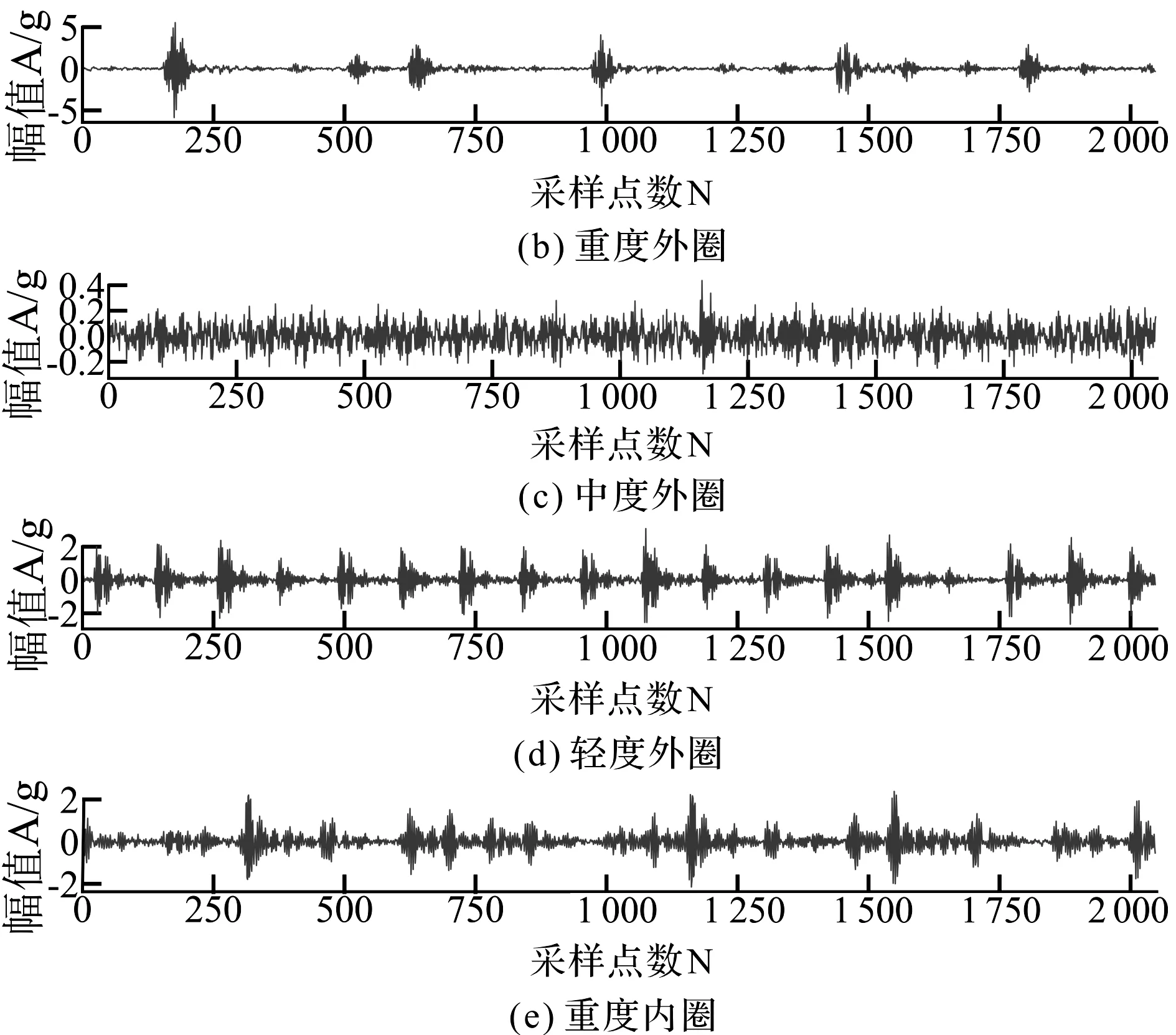
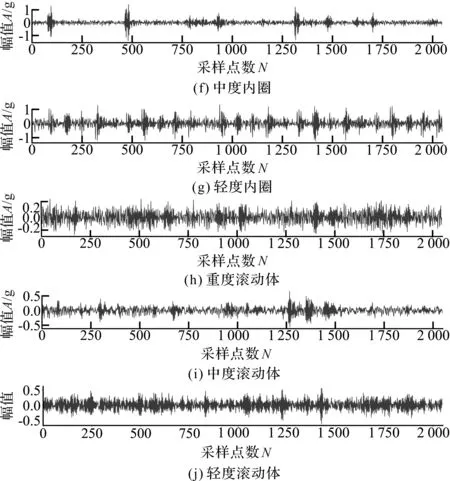

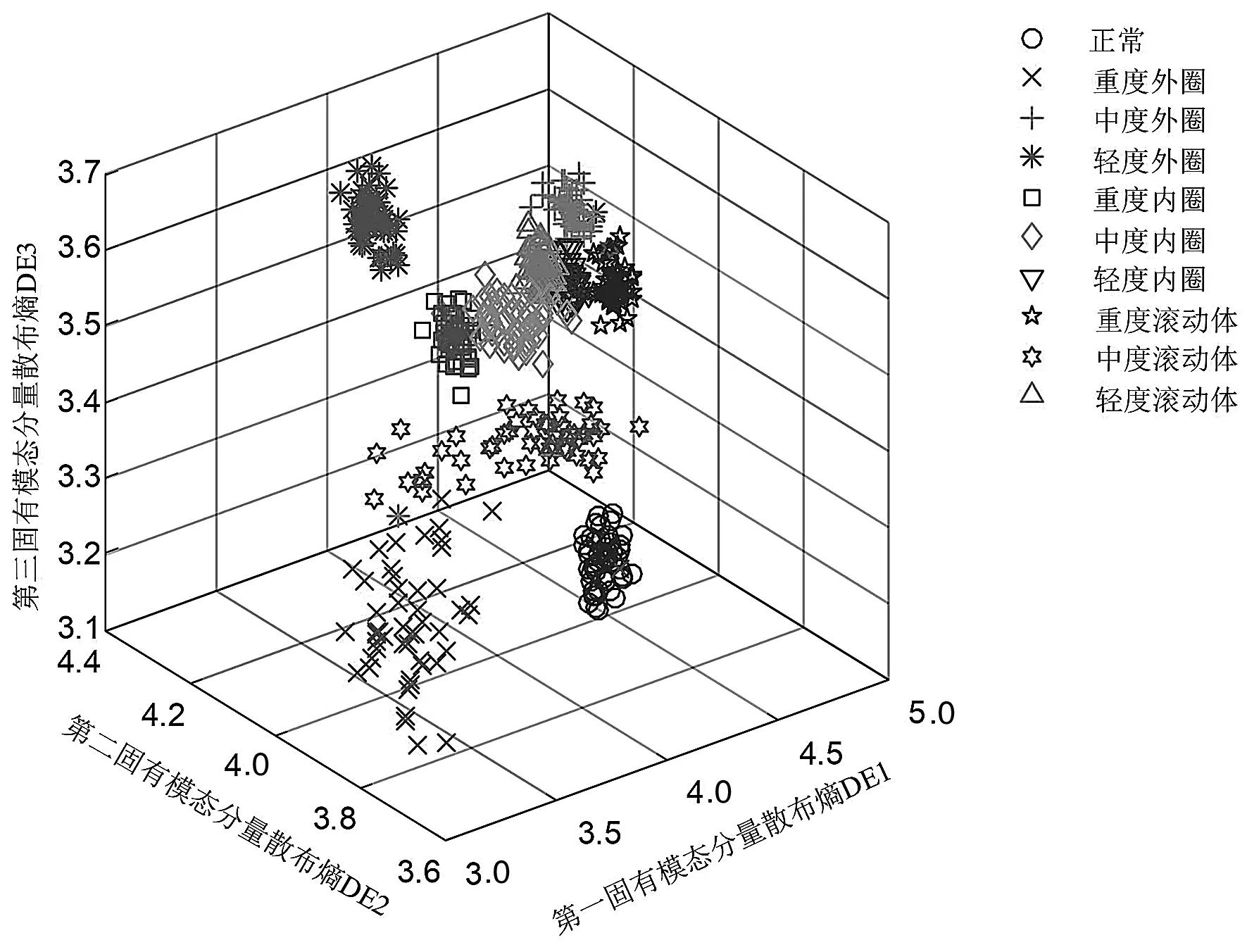
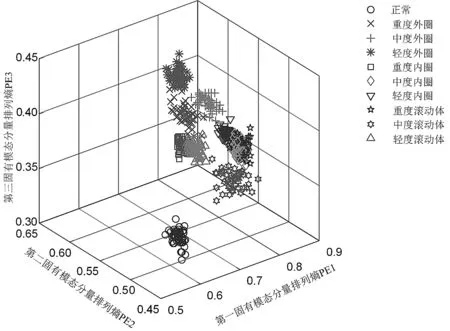


5 结束语

