基于数值模拟的新型摆动泵流场分析*

王子祥,邹 旻,2*,张朦淅,周发戚

(1.常州大学 机械工程学院,江苏 常州 213164;2.常州大学 江苏省绿色过程装备重点实验室,江苏 常州 213164)

0 引 言

泵的种类繁多、分类复杂,按照其工作原理的差异,大致可以分为3类:叶片式泵、容积式泵和其他类型的泵[1]。

往复泵作为容积泵中的一种,相比于其他类型的泵,具有效率高、自吸能力强、运行平稳、结构简单等优点,适合于输送黏性流体介质或者多相流介质,主要在石油化工、医药、食品等行业中得到了广泛运用[2-5]。往复泵的工作原理是通过转子或活塞的往复运动将能量以静压的形式作用于液体。在输送不可压缩液体时,液体可以承受很高的压强,从而获得很高的扬程,同时可以保持与排出压力无关的恒定流量[6-8]。

国内外许多学者已对往复泵进行了广泛的研究。例如,周伟等人[9]通过对往复泵出口管道系统流量脉动和管道振动进行模拟仿真,得到了往复泵振动与流量脉动的状况。针对往复泵流量脉动较大等问题,侯勇俊等人[10]提出了一种新型的往复泵,该往复泵采用凸轮和齿扇、齿条复合驱动的方式,使得三缸往复泵的流量脉动率降低至1.68%。杨国来等人[11]对电磁式往复泵性能影响因素进行了分析,发现柱塞腔内截面积、单向阀弹簧刚度和弹簧预紧力对往复泵的性能都有较大的影响。MA Y等人[12]通过使用计算流体力学(computational fluid dynamics,CFD)的方法,研究了新型五缸双作用往复泵的全循环工作过程,获得了双作用往复泵的瞬态阀运动的状态和流量脉动曲线;该研究结果为往复泵系统的优化提供了一定的参考依据。SUDHAGAR M等人[13]通过使用摆动运动驱动往复泵,使其在最小摆角时仍具有较高的效率。ALBERTO M等人[14]使用三维非定常数值模型,研究了隔膜泵的内部流体与结构之间的相互关系,证实了在低供气压力情况下,止回阀存在更多的不稳定性。

在上述国内外学者的研究中,对使用活塞和隔膜的往复泵研究较多,而对于使用转子的往复泵研究则相对较少,因此,对于往复泵内部流场的情况目前还少有人研究。

针对以上情况,笔者以转子摆动泵为研究对象,即以圆弧形状作为摆动泵的转子形状,利用FLUENT软件对摆动泵进行数值模拟,分析摆动泵工作过程中的压力、速度,以及其流量脉动等的分布状况[15],以期为以后针对转子摆动泵的研究工作提供参考。

1 摆动泵概述

1.1 摆动泵的工作原理

与传统的叶片泵不同,摆动泵是通过转子、定子和两侧挡板来形成其密封容腔的。

摆动泵的机构组成如图1所示。

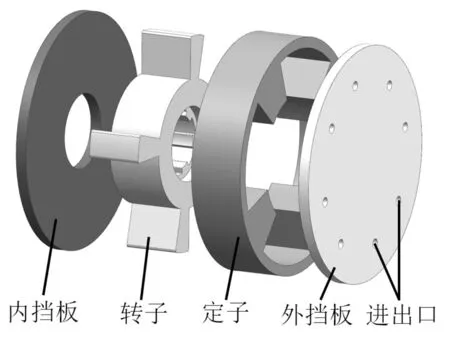
图1 摆动泵的机构组成

根据图1中,摆动泵的工作原理如下:

在摆动泵端面挡板的每个腔体位置开设进出口,通过转子的往复运动可使摆动泵内部的空间发生周期性变化[16],空间的变化会造成其压力的变化,从而产生在进口处的负压和出口处的正压,以此实现对液体的输送和运转。

在摆动泵的工作过程中,通过单向阀来完成吸油、压油过程[17]。

其配流方式如图2所示。

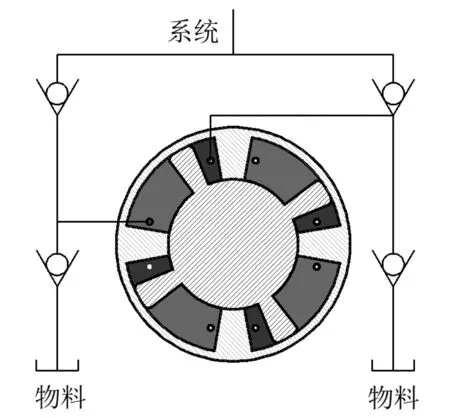
图2 摆动泵的配流方式

该泵使用摆动凸轮机构给转子提供动力,凸轮使用正弦曲线的形状,可保证摆动泵往复摆动,同时减少冲击带来的影响。

此处以一个腔体的进出口作为目标,来分析摆动泵单向阀的配流方式:

当转子进行逆时针旋转时,灰色容腔面积变小排出油液,黑色容腔面积变大吸取油液,油液经过单向阀吸入黑色吸油腔内,灰色压油腔内的油液经过单向阀排到需要油液工作的系统中;

当转子进行顺时针旋转时,灰色容腔面积变大吸取油液,黑色容腔变小排出油液,油液经过单向阀吸入灰色吸油腔内,黑色压油腔内的油液经过单向阀排到需要油液工作的系统中。

使用单向阀的配流方式,转子顺时针或者逆时针旋转,摆动泵都能够顺利地完成吸油和压油。

1.2 摆动泵的转子参数

笔者使用圆弧形状作为摆动泵的转子形状,初步确定了摆动泵的基础尺寸;同时,在强度和刚度满足条件的情况下,改变转子的结构尺寸来提高摆动泵的总体排量。

摆动泵转子的参数如表1所示。

表1 转子尺寸参数

2 摆动泵流场数值模拟

2.1 控制方程

众所周知,流动的流体都要遵守物理基本守恒定律,即质量守恒定律、动量守恒定律和能量守恒定律[18,19]。

(1)质量守恒方程(连续性方程)。流体都要遵守质量守恒定律。因此,对于不可压缩流体来说,其密度ρ的表达式为:

(1)

(2)动量方程。依据动量守恒定律(牛顿第二定律)推导得出,其表达式为:

(2)

(3)湍流模型。Standardk-ε模型是湍流问题求解最常用的模型。

虽然该标准模型适用于大多数湍流问题,但在解决有旋流等非均匀湍流问题时,该标准模型计算的稳定性较差。

RNGk-ε模型是在标准模型上做了一些改动后所得到的模型。采用RNGk-ε模型计算流场时,其精度有所提升。并且标准模型存在旋流较弱的问题时,而RNGk-ε模型通过改善旋转效应,提高了其解决旋转流动问题时的计算精度,所以此处笔者采用RNGk-ε模型。

RNGk-ε模型表达式为:

(3)

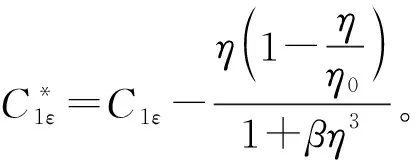
2.2 网格划分

对摆动泵的内部流场进行仿真,既可以选择二维模型,也可以选择三维模型。相比于二维模型,三维模型的网格划分更复杂,网格数量更多,计算更复杂,计算时间也更长。

由于摆动泵的内部流场与横截面流动情况相类似,此处使用二维模型代替三维模型,来对摆动泵的内部流场进行模拟仿真,确保仿真结果符合摆动泵实际运动过程。

二维模型的网格划分一般使用三角形网格或者四边形网格,这两种网格分别对应结构化网格和非结构化网格。由于摆动泵的模型比较简单规整,此处可以使用结构化网格中的四边形网格来进行网格划分。

由于摆动泵内每个腔体的形状都一样,内部流体流动的情况基本相同,可以对摆动泵的二维模型使用周期性边界,即只划分一个腔体的网格,以简化计算的难度。笔者使用ANSYS中的前处理软件ICEM,为摆动泵的二维模型设置周期性边界,并设置旋转对称轴和旋转点旋转角度,对周期性边界进行关联。

此处笔者使用结构化网格单元,对二维模型进行网格划分。其中,最大网格单元设置为0.2 mm,摆动泵单个腔体的二维模型划分为97 101个四边形网格单元,98 315个节点。

网格的数量越多,所需要的计算资源就越大。此处笔者采用结构化的均匀网格,在满足模拟结果所需精度的情况下,不用再增加网格的数量。计算的收敛主要因素是网格质量,次要因素是网格数量。使用ICEM软件自带的网格检查功能Pre-Mesh Quality Histograms命令里的行列式Determinant 3×3×3来检查划分网格的质量。值为1,表示理想的四边形;而0表示网格具有负体积。网格质量以X轴表示,所有的单元在0到1之间。

通常,行列式检查的结果在0.3以上就可以用于大多数求解器,但为了计算结果的精确性,结果最好要大于0.6[20-22]。

网格质量检查结果如图3所示。

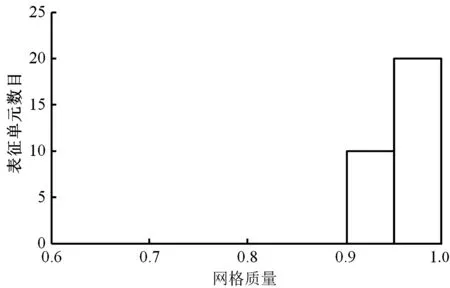
图3 网格质量检查结果

在图3中,纵坐标代表了表征单元的数目,其大小为柱条高度所表示的值,其质量的好坏由定义的柱条数目确定。

根据上述检查结果可知,其最小值为0.946,最大值为1。由此可见,网格质量满足计算要求。

2.3 数值解法

在Fluent中进行数值计算,采用的湍流模型为RNGk-ε模型,壁面附近采用标准壁面函数Standard Wall Functions。

用基于压力的求解方法来求解基本方程,压力项采用PRESTO格式离散,其余项采用二阶迎风格式离散(湍流动能Turbulent Kinetic Energy、湍流耗散率Turbulent Dissipation Rate和Transient Formulation),压力速度耦合方程采用PISO算法求解。

以步长为5e-6,步数为3 200,进行迭代计算。

整个计算过程的流程图如图4所示。

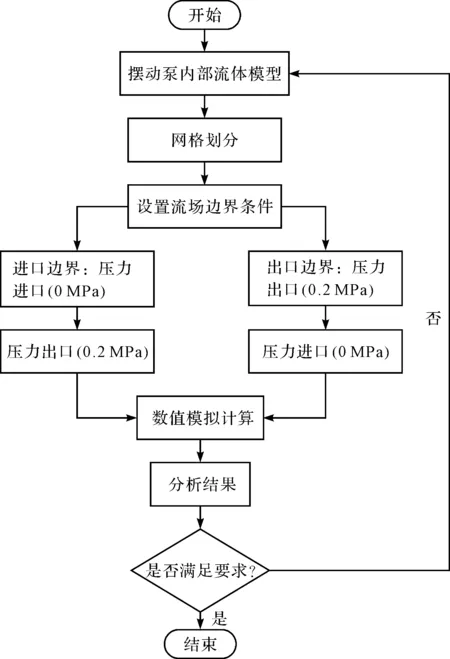
图4 计算流程图

2.4 边界条件设置

笔者根据摆动泵的工况要求,对摆动泵的二维模型添加边界条件:入口类型设置为压力入口Pressure-inlet,压力大小0 MPa;出口类型设置为压力出口Pressure-outlet,压力大小0.2 MPa,其余边界条件设置为wall。传输介质为油,密度为960 kg/m3,黏度为0.048 kg/m·s-1。

由于转子需要运动,笔者使用动网格技术,转子的壁面设置为运动边界,转子的运动使用UDF的方式进行驱动。摆动泵是往复运动的,在摆动泵运动过程中,进出口的边界是变化的;在摆动泵的一个周期内,其进口的边界由原来的压力进口Pressure-inlet转变为压力出口Pressure-outlet,其出口由原来的压力出口Pressure-outlet转变为压力进口Pressure-inlet。

在摆动泵往复运动过程中,进口和出口需要来回转换,所以它们的进出口压强大小也不是固定的,此时常规的给定数值这种方法就不能使用了。笔者通过使用UDF自定义的方式,来给定它们进出口的压强大小,让它们的压强大小在往复运动中产生变化。

3 计算结果分析

为了进一步深入分析摆动泵模型内部流场的瞬态特性,笔者在周期时间为0.016 s,介质黏度为0.048 kg/m·s-1,进出口压差为0.2 MPa的工况条件下,对泵体内部压强、速度等进行分析,以得到不同时刻的压强、速度等的分布云图。

3.1 压力分析

在进出口压差为0.2 MPa的工况条件下(初始进口压强设置为0 MPa,出口压强设置为0.2 MPa),笔者对摆动泵进行数值计算,得到在不同时刻的压力分布云图,如图5所示。

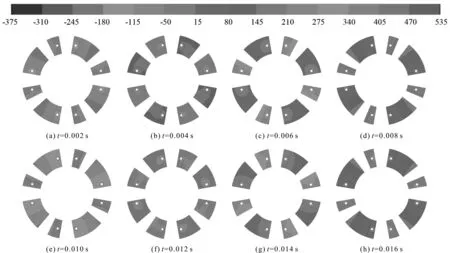
图5 不同时刻压力分布云图(单位:kPa)

从图5中可以发现:

在任意时刻,腔体内部压强云图颜色变化比较明显,腔体内部的压强分布不均匀。在不同时刻,最小压强的位置集中在进口位置,泵腔内部转子和壁面形成的封闭腔室内的压力变化明显。随着转子的转动,泵腔内部的压力也发生了较大的变化,主要是因为转子的运动时间变长了,随着时间的累积,腔体内部流体获得的能量也慢慢增多。在运动过程中,转子的速度是变化的,随着速度的变大,腔体内部的压力也变大,最大的压力为0.52 MPa。转子逆时针转动,吸油腔容积逐渐变大,在进油口处形成一定的负压,油液从进口处被吸入泵腔内部;随着转子逆时针转动,出油腔容积逐渐变小,在出油口周围形成较大的正压,油液从出油口被排出。

3.2 速度分析

不同时刻的速度流线图如图6所示。

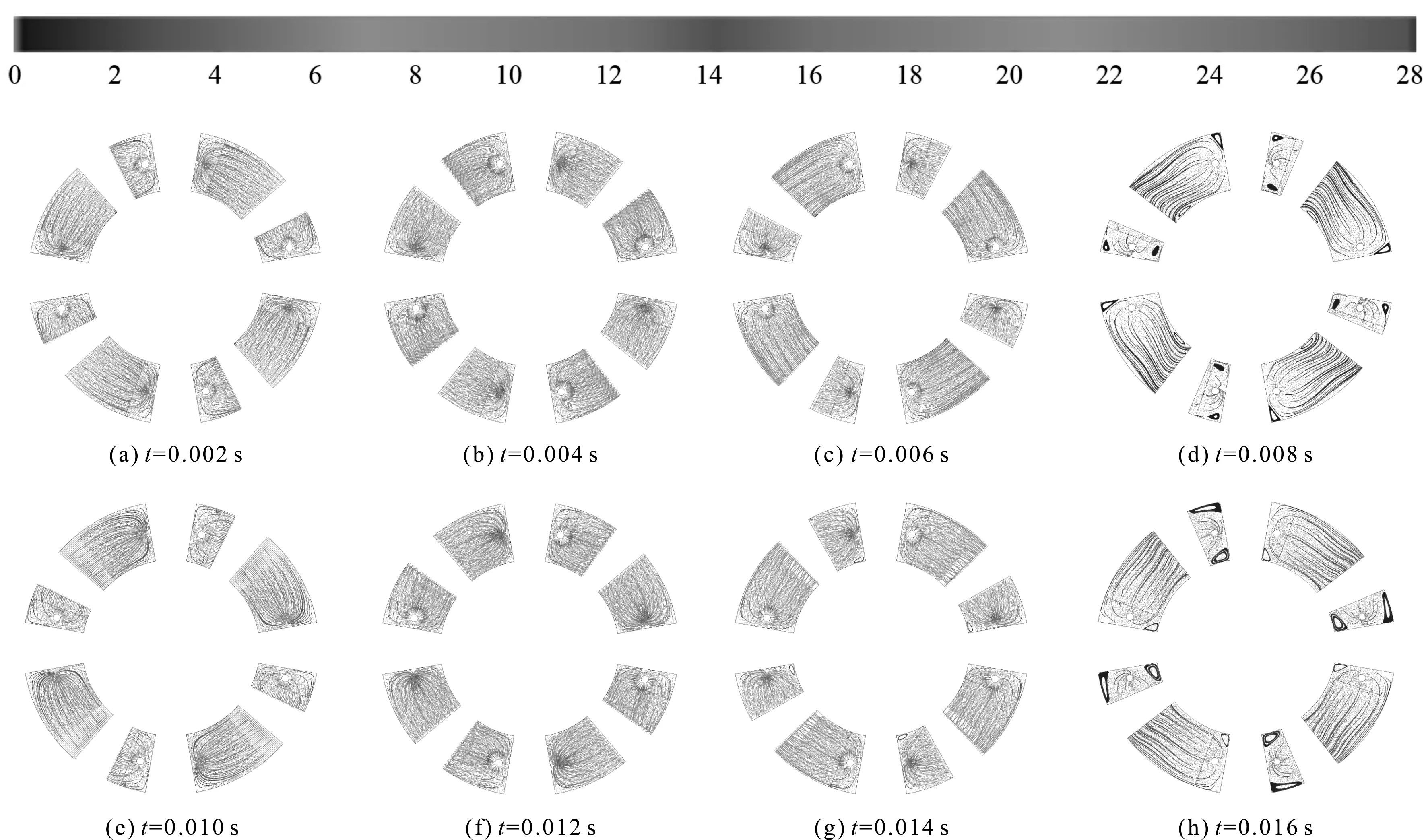
图6 不同时刻的速度流线云图(单位:m/s)

从图6中可以看出:

流体在腔体内部流动的各个时刻,其速度矢量的分布比较均匀,在进出口处位置的速度最大,最大的速度为8 m/s。腔体内部流体的速度跟转子转动的速度相关,转子转动得越快,内部流动的速度也越快;反之,内部流动的速度越慢;在0.008 s和0.016 s时,其流速几乎为0,这是因为转子需要改变方向,所以速度接近于0;且在这两个时刻,云图上面出现了较小的涡流,由于涡流的速度较小,不会在腔体内部产生较大的流量脉动、压力损失,也不会改变流速的方向。

3.3 流量脉动

笔者通过数值模拟的方式,得到了摆动泵出口流量的脉动曲线,如图7所示。

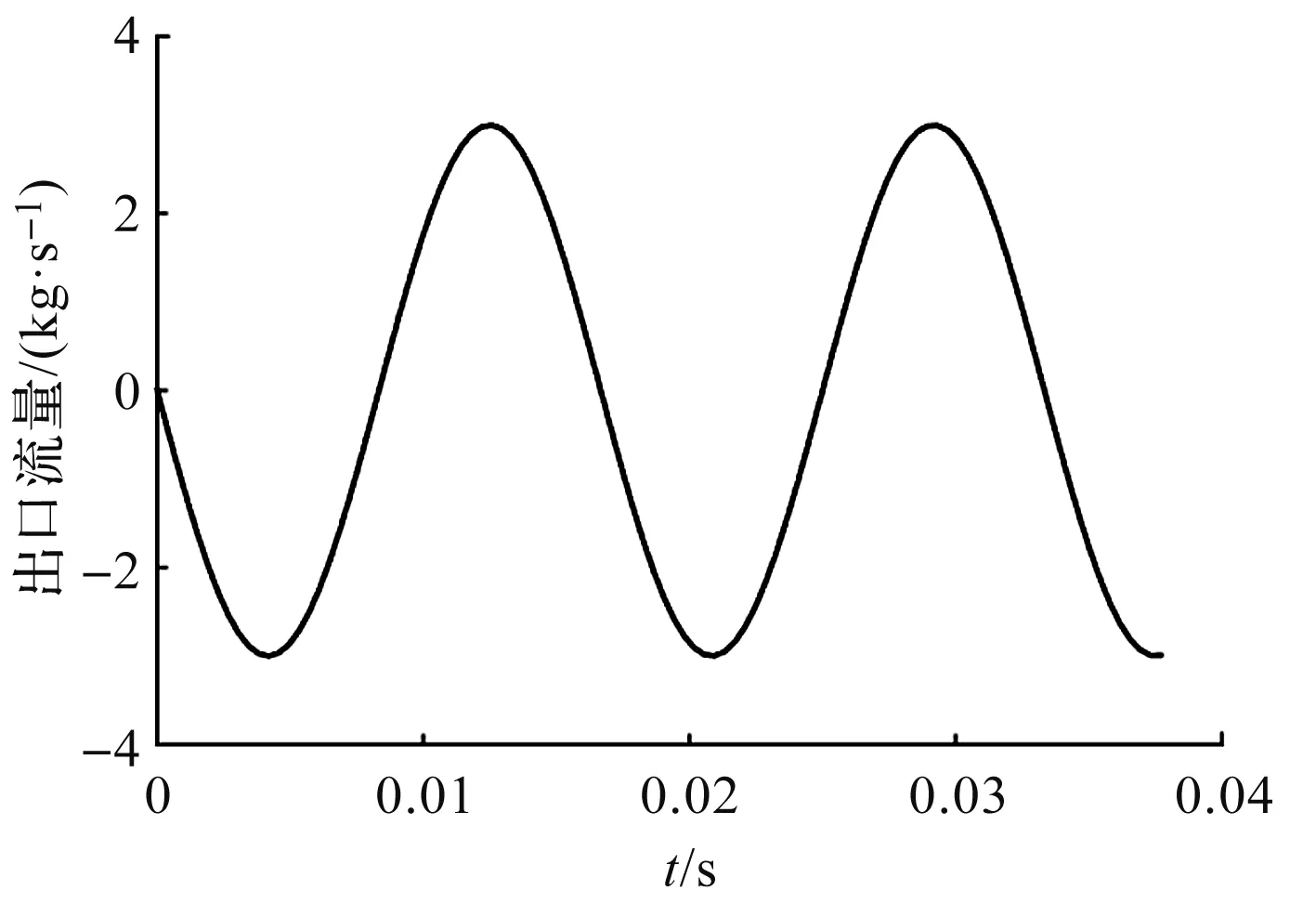
图7 出口流量脉动曲线

由图7可知:瞬时流量的大小和速度有关,最大的瞬时流量是在0.004 s和0.012 s时。在速度最大时,最大瞬时流量为3 kg/s;

由图7还可知:该摆动泵的周期性和重复性较好,而且周期时间为0.016 s,且摆动泵的流量脉动曲线与转子的加速度具有相同的波形。

3.4 减小流量脉动方法

为了减小摆动泵的流量脉动,笔者提出了一种解决方法,即使用多层错位放置的方法,来增加摆动泵的层数,减小流量脉动,使其流量峰值错开,流速更均匀,实现流量的连续输送。

4 结束语

为了解决往复泵结构复杂和流量脉动大的问题,笔者以转子摆动泵为研究对象,利用FLUENT软件对摆动泵进行了数值模拟,分析了摆动泵工作过程中的压力、速度,以及其流量脉动等的分布状况。

研究得到以下结论:

(1)分析转子运动过程中,腔体内部压力分布不均匀,随着转子转动速度的增大而增大。在吸油腔体内部产生最小的压力,在压油腔体内部产生最大的压力;

(2)在0.002 s、0.004 s等瞬时时刻,腔体内部速度分布比较均匀,速度大小近似一样。但在不同的瞬时时刻,它们之间的速度是不一样的,跟随着转子转动速度的增大而增大,最大速度都集中在进出口位置;

(3)流量脉动曲线与转子的加速度具有相同的波形,且具有良好的周期性和重复性。

在后续的工作中,笔者将继续对摆动泵的流量脉动问题做进一步的研究,尝试使用多层错位放置法,并验证其在流量脉动抑制上的可行性。