离心泵启动过程内部流动瞬态特性分析*

马晓堂,宋文武,舒乙宸,陈洪阳

(西华大学 能源与动力工程学院,四川 成都 610039)

0 引 言

离心泵是一种流体机械[1],被广泛应用于工农业生产中的。过去,研究人员更多关注的是泵在长期运行过程中的稳定性,其研究方向也主要是针对泵在稳定工况下的内部流动特性,及内部流动特性对泵性能的影响[2]。

但随着工程领域的不断发展,离心泵的应用范围也在不断扩大。现阶段,有关离心泵的主要研究方向有:离心泵过渡过程的瞬态特性、离心泵启动过程中可能产生的各种情况、离心泵启动过程中不同时刻的瞬态流动特性、离心泵启动过程中对边壁产生的冲击作用等。

目前,国内外研究人员对于离心泵在启动过程中的动态特性做了一些相关工作。日本学者TSUKAMOTO H等人[3]采用数值计算和实验的方式,对低比转速离心泵额定转速的瞬态特性进行了研究,研究发现,当其按照正弦规律变化时,转速波动为12%;并且发现转速波动频率越高,其瞬态与准稳态之间的性能波动越剧烈。LEFEBVRE J等人[4]针对高比转速离心泵,在3种叶轮启动加速度方案下的启动与停机进行了实验研究,研究发现,在离心泵启动初期,压力脉冲会导致无量纲压力系数超出假设的准稳态预测值,而当初期压力脉冲结束后,瞬时无量纲压力系数相较于准稳态值降低了37%。法国学者DAZIN A等人[5]在瞬态条件下,对离心泵叶轮的功率、扬程和内部扭矩进行了研究,发现在瞬态过程中,离心泵的瞬态效应与内部的流场演化相关。王乐勤等人[6]采用功率键合图法,对叶片泵启动过程中的动态特性进行了研究,发现键合图法可用于对叶片泵启动过程中的动态特性进行研究。吴大转等人[7-9]采用飞轮蓄能系统,对离心泵不同加速度的启动过程进行了实验研究,发现较大的启动加速度能使离心泵的性能更快地到达稳定点,并且冲击扬程明显增大。

综上所述,目前对于离心泵整体启动过程中的内部流动研究,以及其瞬态非定常的研究相对较少,尤其是对离心泵启动过程中的水力进行优化方面,还没有成熟的理论体系。

笔者以一台比转速为146的中比转速离心泵为研究对象,利用CFD软件,通过全流道三维准稳态和瞬态非定常数值模拟,研究离心泵启动过程中,不同时段内部流道压力分布、叶轮叶片以及流道出口压力脉动的情况,以期为离心泵水力优化、离心泵配套电机选择及其系统的可靠运行提供理论基础。

1 计算模型及网格划分

1.1 计算模型参数

笔者运用UG软件建立离心泵的三维实体模型。为了保证仿真模型中的湍流发展更加稳定,提高模拟结果的准确性,笔者对泵的进口段和出口段进行适当的延伸,延伸长度为进、出口段直径的5倍。

离心泵的模型参数如下:

设计流量Qt=160 m3/h,扬程H=15 m,转数n=1 450 r/min,比转速ns=146,叶轮进口直径D=142.5 mm,叶轮出口宽度b2=26.4 mm,叶轮外径D2=240 mm,叶片数Z=6。

离心泵的三维模型图如图1所示。

图1 离心泵(比转速为146)三维模型图

1.2 网格划分与无关性检验

为了提高数值计算的精确度和可靠性,笔者采用ICEM软件,对离心泵三维模型的全流道进行结构化网格划分。对不同构件单独进行网格划分,针对叶轮叶片部位和蜗壳隔舌位置进行加密,以提高其计算的准确性[10];同时对网格进行无关性验证。

网格无关性验证如表1所示。

表1 网格无关性验证

由表1可知:随着网格数的增加,泵的效率呈现先增大,然后逐渐趋于平缓的特点;当网格数目达到3 783 873时,泵的效率不再继续增加。

为了方便计算,笔者确定本次模拟计算的网格数为3 783 873(表1中的方案3)。

离心泵的网格划分图(叶轮及蜗壳)如图2所示。

图2 离心泵网格划分图(叶轮及蜗壳)

2 数值计算方法

2.1 计算模型和边界条件

由于RNGk-ε湍流模型考虑了壁面上的大尺度分离[11],从而能够较好地模拟离心泵启动过程内部的分离和漩涡流动,此处笔者选择RNGk-ε湍流模型进行数值模拟计算。

在瞬态操作条件下,离心泵表现出来的特性可由外特性来描述,而外特性的变化直接由内部非定常流动状态所决定[12]。笔者利用CFX软件提供的二次开发接口,通过编写用户自定义函数CEL,来加载转速变化规律,模拟离心泵启动过程的转速变化过程。

转速变化函数CEL表达式如下[13]:

(1)

式中:n—相对应时刻的瞬时转速,r/min;ns—离心泵额定转速,r/min;step函数—CFX软件中所使用分段函数;Ttol—整个启动过程的转速加速时间,Ttol=1 s;t—时间变量,s。

离心泵转速变化过程中,考虑到其流量随着泵转速的变化而变化,因此,在设置边界条件时,笔者需要通过函数CEL表达式来控制质量流的不断变化[14-16]。

根据相似定律中流量与转速之间的关系,此处流量的变化规律为:

(2)

式中:n—相对应时刻的瞬时转速,r/min;Qt—离心泵设计流量,Qt=160 m3/h。

对应step函数启动过程转速变化图如图3所示。

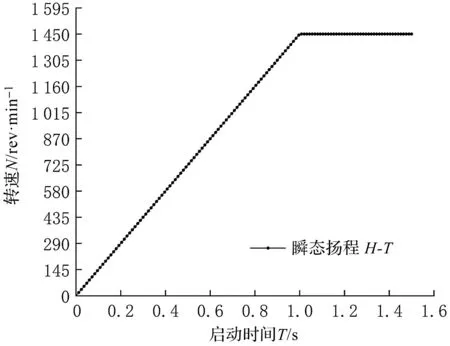
图3 Step函数启动过程转速变化图

在计算边界条件中,进口条件设置为Total pressure,参考压力设置为1 atm,出口边界条件设置为Mass flow[17,18]。网格节点均采用GII模式。

对于叶轮和进口段、叶轮和蜗壳之间的动静耦合交界面,笔者采用Frozen Rotor模式进行衔接,其壁面为无滑移壁面,其他壁面均采用静止无滑移壁面,收敛精度为10-6。

在非定常模拟过程中,动、静耦合界面采用Transient Frozen Rotor模式。笔者将定常模拟结果作为非定常计算的初始条件,并在保证计算精度的前提下,根据转速变化情况设置计算总时间和输出频率[19]。

2.2 压力脉动监测点设置

为了分析离心泵启动过程中,其内部瞬时流动状态以及压力脉动情况,笔者在离心泵叶片工作背面不同位置设置监测点y0～y5(叶片进口、中段、尾部),在流道出口位置设置监测点LD1～LD6;其中,流道出口位置的监测点是固定位置。

监测点设置图如图4所示。

图4 监测点设置图

3 泵启动过程仿真及分析

3.1 外特性分析

离心泵启动过程中外特性曲线图如图5所示。

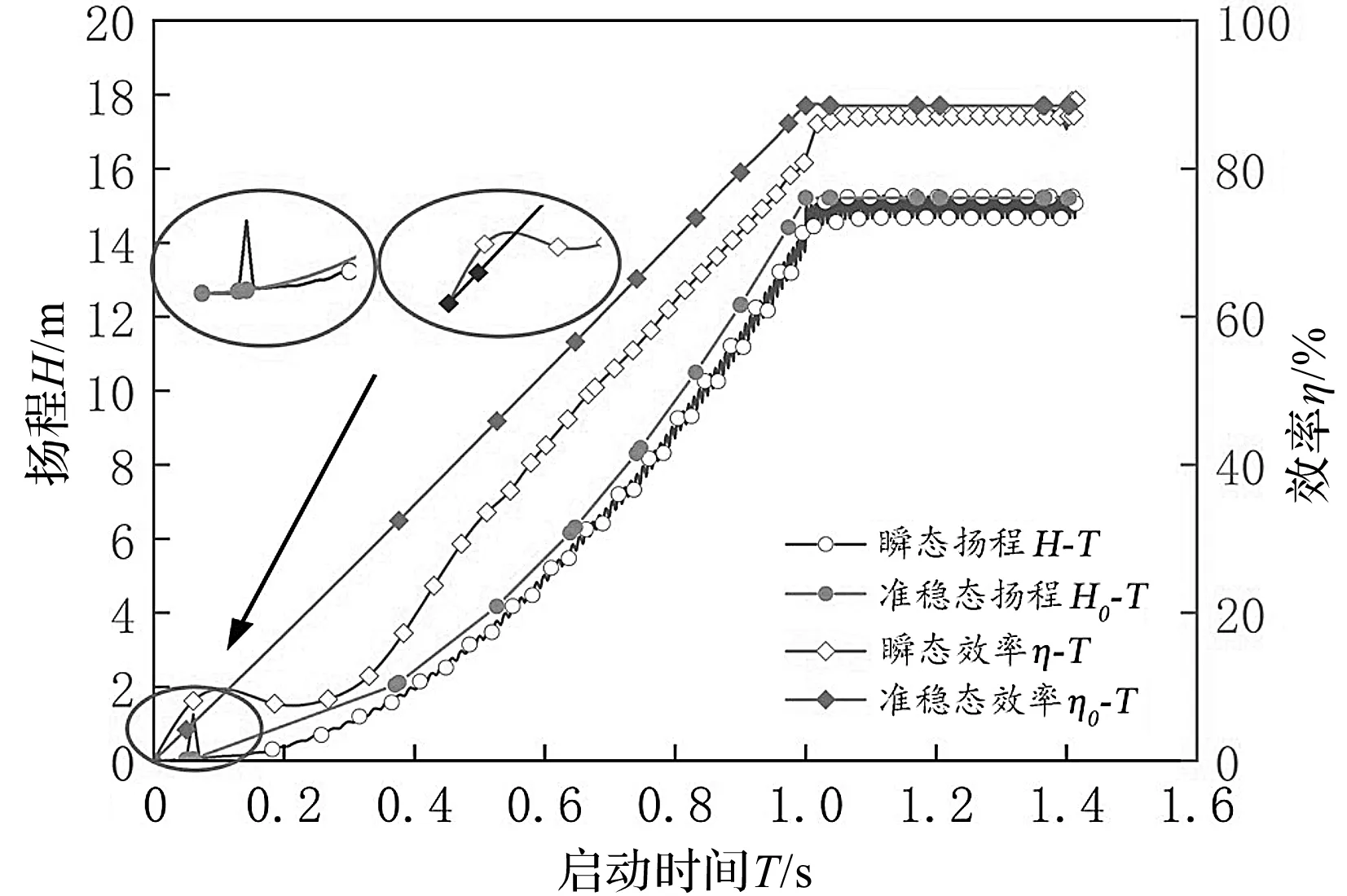
图5 启动过程外特性曲线

由图5可知:在离心泵的启动过程中,整体扬程和效率都呈现出逐渐上升的趋势;但是在启动初期,其瞬态扬程和瞬态效率均出现脉冲现象,其值均高于准稳态时的扬程和效率;脉冲结束后很快出现下降趋势,此时的瞬态值均低于准稳态值;

随着启动时间的增加,其瞬态扬程和效率逐渐靠近准稳态时的值,当T=1 s时刻,其瞬态扬程和效率基本与准稳态时的值相重合,随后扬程出现波动现象。

该离心泵启动过程的脉冲现象是指,在离心泵的启动过程中,其扬程和效率等参数在某些时间区间呈现连续规律性的变化,但是由于在启动过程中,离心泵的叶轮转速快速变化的原因,某些时刻离心泵内部的流体流动状态会遇到突然性的改变;由于这个变化时间非常短(相对于整个启动过程),该突变或跳跃过程可以视为在某个时刻瞬时发生的,并且在突变过程后迅速降低,回归到原先连续规律性的渐变中。

在离心泵启动过程初期,其瞬态扬程和效率出现脉冲现象,可能是因为在启动起始阶段,叶轮突然转动导致动、静干涉产生压力脉冲造成的。

在脉冲现象之后,其瞬态扬程和效率下降,并且其值低于准稳态值;其后转速到达额定转速阶段,瞬态扬程和效率与准稳态值出现重合,并且出现波动现象,这可能是由于现时刻转速未达到额定转速,而导致其受到叶片环量的影响。

3.2 内部流道压力分布

在离心泵的启动过程中,不同时刻泵的瞬态模拟内部流道的压力分布情况,如图6所示。

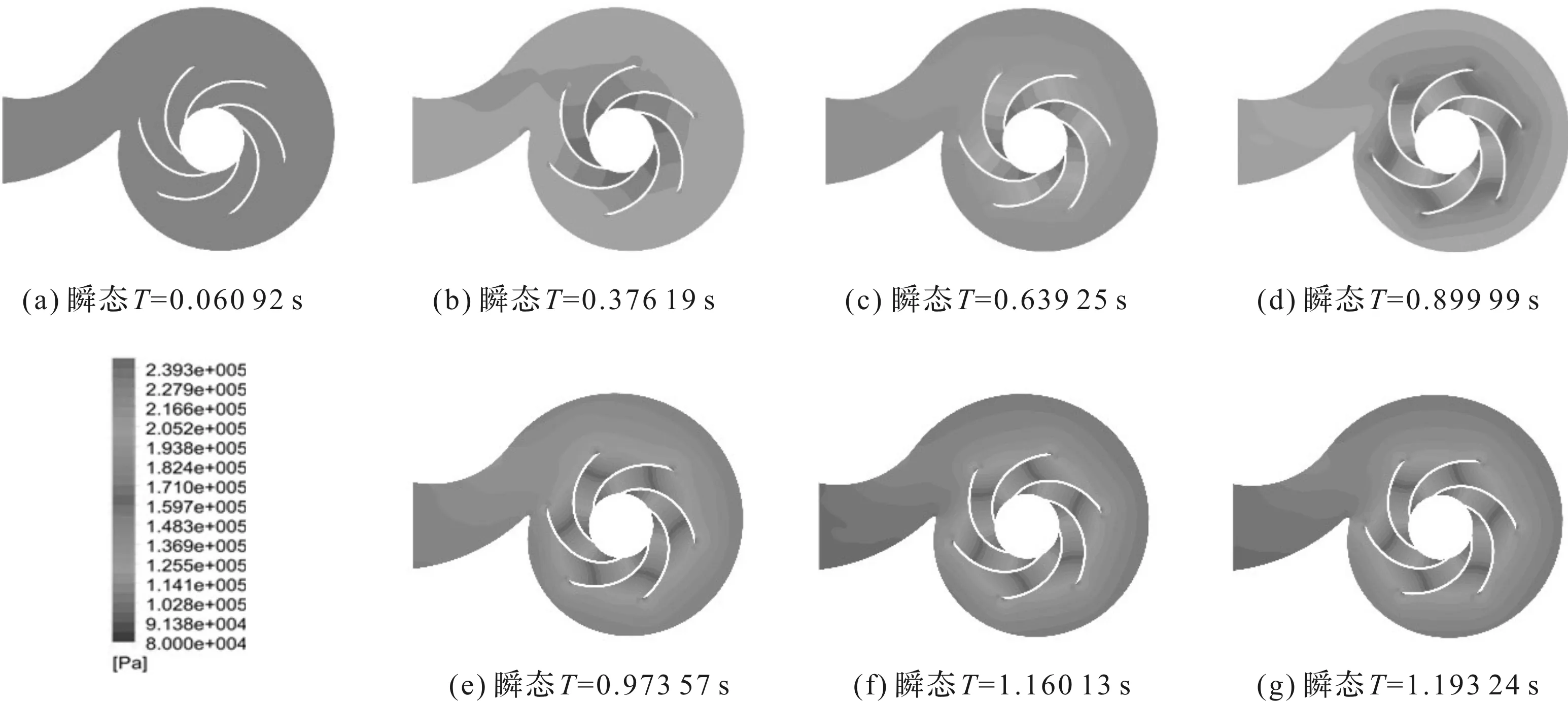
图6 启动过程离心泵瞬态内部压力云图

不同时刻泵的准稳态模拟内部流道的压力分布情况如图7所示。

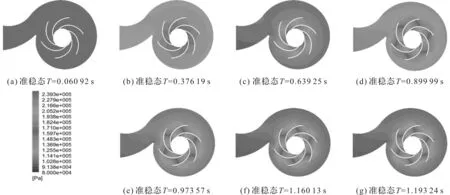
图7 离心泵启动过程准稳态内部压力云图

离心泵瞬态和准稳态内部压力增减百分比情况如表2所示。

表2 离心泵瞬态和准稳态内部压力增减百分比

由图6和图7可知:离心泵启动过程中,在对准稳态和瞬态进行模拟时,其内部压力分布存在差异;在离心泵启动初期T=0.060 92 s时刻,离心泵瞬态压力分布大于准稳态压力分布;

并且由表2可知:(1)隔舌位置处的压力分布突变最为明显,当T=0.060 92 s时,瞬态隔舌处压力大于准稳态3.51%;而当T=0.376 19 s时,瞬态隔舌处压力小于准稳态11.22%;(2)叶轮流道出口处压力变化跨度最大,当T=0.060 92 s时,瞬态流道出口处压力大于准稳态3.84%;当T=0.973 57 s时,瞬态流道出口处压力小于准稳态28.82%;

随着启动时间的递进,离心泵内部瞬态压力分布均小于准稳态,当T=1.160 13 s时刻,除叶轮流道出口段和隔舌部位外,其余瞬态压力分布和准稳态基本一致,且瞬态压力分布出现一定程度的波动现象,满足外特性中启动初期出现的瞬态效应,且整个离心泵内部瞬态和准稳态压力分布情况为逐渐增长,当瞬态模拟转速达到额定转速时刻后,瞬态压力分布也出现波动。

3.3 压力脉动分析

叶片不同位置监测点y0-y5的压力脉动时域图如图8所示。

图8 叶片压力时域图

由图8可知:在启动过程中,监测点的压力值随着时间的改变呈现出现明显的周期性变化规律,且在启动初期也出现脉冲现象,整体压力值都在当T=1 s时刻后出现稳定的周期变化;其中,监测点y0的压力值随着时间的改变逐渐降低,监测点y1的压力值随着时间的变化基本处于稳定状态,其余监测点的压力值都随着时间的改变逐渐增加,达到T=1 s时刻后出现稳定的周期变化。

为了探究离心泵启动过程中,叶片部位的压力脉动情况,笔者将压力脉动时域图经过快速傅里叶变换,得到了其频域图。

叶片不同位置监测点y0-y5的压力脉动频域图如图9所示。

图9 叶片压力脉动频域图

从图9中可以明显观察到:出现最大的压力幅值为监测点y5处,最小压力幅值为监测点y1处。由此可见,离心泵的启动过程对叶轮叶片的压力脉动具有明显的影响,其中影响最明显的是叶片尾部,相对影响最小的则为叶片头部1/5处。

出现上述现象的主要原因是,在离心泵启动过程中,叶片头部流道相对较窄,流体受到叶片的约束,规则地向后方流动,叶片尾部则流道较宽,叶片对流体的约束较少;当离心泵转速没有到达额定转数时,在叶片尾部流道内部流动相对混乱,故该叶片头部压力脉动的幅值较小,而叶片尾部会出现最大压力脉动幅值。

在离心泵启动过程中,不同流道出口的压力脉动时域图如图10所示。

图10 流道出口压力脉动时域图

由图10可知:在离心泵启动过程的初期,压力会出现一个脉冲现象;随后在启动过程中,各个流道出口监测点的压力值会随着时间的改变呈现出明显的周期性变化规律,整体压力值都在T=1 s时刻后呈现稳定的周期性变化,且幅值十分接近。

出现上述现象的主要原因是,在离心泵启动过程的初始阶段,转速尚未达到额定转速,内部流体流动发展的不充分导致压力脉冲现象的出现;随着时间的改变,离心泵内转速达到设计工况,内部流动趋于稳定,整个机组达到额定工作状态。

离心泵启动过程中,不同流道出口(LD1-LD6)的压力脉动频域图,如图11所示。

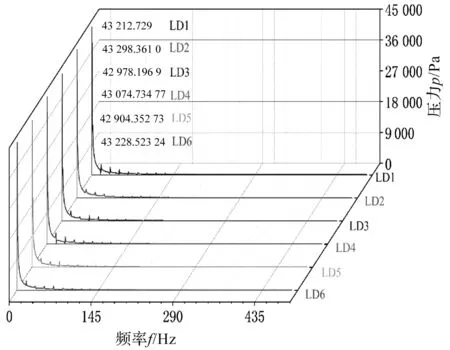
图11 流道出口压力脉动频域图

由图11可知:流道出口各个监测点位置的压力脉动变化情况基本一致,且各个监测点位置的最大脉动幅值也基本相等,最大幅值为监测点LD2的43 298.361 0 Pa,最小幅值为监测点LD5的42 904.352 73 Pa,差距为0.91%;

并且各个监测点的主频均为0.732 63 Hz,为本次研究离心泵转频f=24.166 7 Hz的0.030 3倍,说明在离心泵启动过程中,离心泵叶轮的流道出口处可能会出现很强烈的低频压力脉动。

4 结束语

笔者以一台比转速为146的中比转速离心泵为研究对象,利用CFD软件,通过全流道三维准稳态和瞬态非定常数值模拟,研究离心泵启动过程中,不同时段内部流道压力分布、叶轮叶片以及流道出口压力脉动的情况。

研究结论如下:

(1)在离心泵的启动过程中,整体扬程和效率均呈现出逐渐上升的趋势,在启动初期瞬态扬程和瞬态效率均出现脉冲现象,脉冲结束后很快出现下降趋势,且均低于准稳态值,当T=1 s时刻瞬态扬程和效率基本与准稳态重合;

(2)在离心泵启动初期T=0.060 92 s时刻,离心泵瞬态压力分布大于准稳态压力分布,当T=1.160 13 s时刻瞬态压力分布和准稳态基本一致,其余时间瞬态压力分布均小于准稳态压力分布;

(3)各个监测点的压力脉动主频均在0.030 3f出现,其中叶片上压力脉动最大幅值出现在y5处,其值为42 833.769 Pa,最小幅值出现在y1处,其值为901.205 Pa;流道出口处各个监测点最大脉动幅值则是基本相等,最大差距为0.91%。

该研究涉及的离心泵启动过程,只停留在对一次函数的启动方案进行模拟。关于更多的启动方案下的情况,及其启动过程的计算方法,还需要在之后的研究中进行进一步的探索。