铰接轮式装载机的横向动力学建模分析*

王顺桀,刘前结,李晨阳,叶军君,祝青园

(厦门大学 机电工程系,福建 厦门 361102)

0 引 言

铰接轮式装载机是世界上使用量最大的工程机械之一[1],其主要功能是对松散物料进行铲装及短距离运输作业。铰接轮式装载机的车身结构主要包含前、后两个铰接相连的车体,通过液压缸推动活塞控制前、后车体之间的偏航角,以实现转向[2]。由于铰接轮式工程车辆具有变结构、变质心与变载荷等强非线性特点,同时包含铰接液压转向、前后车体与后轴摆动桥,其动力学模型的建立存在困难。

由于铰接轮式装载机结构的特殊性,国内外学者对其动力学模型进行了深入的研究。

黄建等人[3]利用ADAMS对不同工况下铰接轮式装载机铲斗液压系统进行了仿真,为铰接轮式装载机的设计提供了参考依据。汪建春等人[4]为了简铰接轮式工程车辆的原地转向动力学模型,将车辆的原地运动简化为以较重车车轴中点为曲柄固定点的曲柄连杆运动,但该动力学模型不适用于行驶过程中的铰接轮式工程车辆。窦凤谦等人[5]建立了地下矿用铰接装载机的动力学模型,并将其运用于实际,实现了对装载机的路径跟踪和避障控制;但由于该研究假设车辆行驶路面为水平路面,该结果不适用于在非水平地面行驶的铰接轮式装载机。

同时,铰接轮式装载机变结构变质心的特点导致其易侧倾失稳,因此,部分学者通过车辆行驶稳定性分析,将各种优化的约束指标应用于车辆动力学模型的建模与分析。

AZAD N L等人[6]建立了铰接轮式装载机的水平运动线性模型,初步分析了装载机的行驶稳定性;但由于其线性简化,不适用于大转向角转弯的情况。宾泽云等人[7]通过建立水平地面上的铰接轮式装载机动力学模型,分析了速度对车辆行驶稳定性的影响,但没能给出定量的约束指标。祝青园等人[8]围绕铰接轮式装载机的横向稳定性和动力学模型进行研究,提出了稳态余量角等横向稳定性指标;但由于没考虑转向角改变引起的惯性力,因此,该结果难以适用于转向角改变的车辆动态行驶过程。

在其他方面的研究中,通常还会利用横向加速度和横摆角速度对横向稳定性进行评价[9,10],但因为铰接轮式装载机具有变结构与变质心特性,所以,此类常规车辆约束性指标难以准确反映铰接轮式装载机的侧倾稳定性。

上述研究所提出的动力学模型均假设车辆行驶路面为水平路面,没有考虑地面倾斜引起的重力、轮胎垂直载荷力等动力学参数改变,不适用于非水平地面;部分动力学模型难以准确描述行驶过程中,铰接转向角改变引起的动力学特性变化。并且,现有的铰接轮式装载机横向动力学模型对模型约束性考虑较少,此类约束性指标难以准确反映其非结构环境中变转向角行驶的侧倾稳定性。

为此,笔者建立铰接轮式装载机横向动力学模型,并进一步分析动力学模型的约束条件,通过比例样机行驶实验,来验证动力学模型的有效性。

1 铰接轮式装载机动力学建模

为了建立铰接轮式装载机的横向动力学模型,笔者首先分析液压转向系统的结构和动力学原理,然后通过装载机坐标系和全局坐标系的转换,建立其前、后车体的运动学模型,并进一步构建整车的横向动力学模型,分析在动力学特点下装载机动力学模型的约束条件。

为验证模型的有效性,笔者搭建比例样机进行侧翻约束实验和转向行驶实验,其技术路线如图1所示。

图1 铰接轮式装载机动力学建模流程图

1.1 液压转向系统分析

液压转向系统是影响装载机转向行驶规律的主要部件,因此,建立装载机的横向动力学模型需要对其进行分析。

铰接轮式装载机液压转向活塞的布置如图2所示。

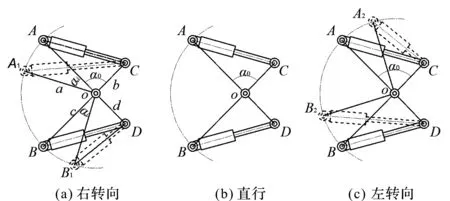
图2 活塞长度与转向角关系的示意图

在图2中,A、B点与后车体铰接,C、D点与前车体铰接。以铰接中心为圆心、后车体为参照,前车体绕后车体相对转动。设∠AOA1=∠BOB1=α,∠AOC=∠BOD=α0,AC=A1C=a,BD=B1D=b,可以获得转向角与活塞AC轴长度p1的关系为:

(1)

车辆液压转向系统的结构刚度通常为常数KR,设转向系统交界处的摩擦阻力和泄漏引起的阻尼为扭转阻尼CR,则液压缸产生的转向力矩[11]为:

(2)

通过上述公式可以获得活塞长度与转向角的关系,同时获得转向力矩,以用于前后车体的动力学建模。

1.2 前后车体运动学分析

为了获取装载机的运动轨迹,需要对其进行运动学分析,建立车辆坐标与全局坐标之间的联系,获得前后车体之间动力学参数的耦合关系。

在常规车辆的运动学和动力学模型研究中,常使用单车模型[12]对运算过程进行简化。单车模型将常规车辆4个前后车轮简化为在车辆中心轴上的2个等效车轮。等效后轮与车体方向一致,等效前轮转动可以改变行驶方向。等效简化法可显著地缩减模型的计算量,提高运算效率。相比于常规车辆,铰接轮式工程车辆没有转向轮,而是通过改变前后车体之间的转向角来实现转向。

因此,笔者建立铰接转向单车模型,如图3所示。

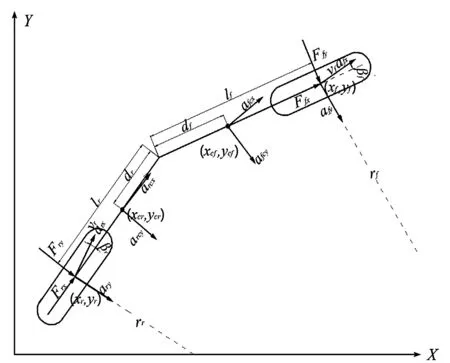
图3 铰接转向单车模型xcf—前车体质心横坐标;ycf—前车体质心纵坐标;xcr—后车体质心横坐标;ycr为—后车体质心纵坐标;xf—前车轴中点横坐标;yf—前车轴中点纵坐标;βf—等效前轮的侧偏角;βr—等效后轮的侧偏角;df—前车体质心到铰接点距离;dr—后车体质心到铰接点距离;lf—前轴中点到铰接点的距离;lr—后轴中点到铰接点的距离;rf—前车体行驶的曲率半径;rr—后车体行驶的曲率半径;vfx—前轴中点纵向速度;vfy—前轴中点横向速度;vrx—后轴中点纵向速度;vry—后轴中点横向速度;arcx—后车体质心纵向加速度;arcy—后车体质心横向加速度;afcx—前车体质心纵向加速度;afcy—前车体质心横向加速度;afy—前轴中点横向加速度;afx—前轴中点纵向加速度;ary—后轴中点横向加速度;arx—后轴中点纵向加速度;Ffy—等效前轮横向力;Ffx—等效前轮纵向力;Fry—等效后轮横向力;Frx—等效后轮纵向力

在图3中,以前轴和后轴的中点速度作为简化模型前后车轮的速度,通过改变前后车体之间的夹角,以改变行驶方向。根据前后车体相对关系可以得到车体结构主要位置全局坐标:

(3)

(4)

(5)

(5)

式中:xo—车辆整体运动瞬心横坐标;yo—车辆整体运动瞬心纵坐标;ρf—前车体行驶曲率;ρr—后车体行驶曲率;kf—前车体与x轴正方向的夹角;kr—后车体与x轴正方向的夹角。

(7)

(8)

式中:mr—后车体质量;mf—前车体的质量。

根据铰接轮式工程车辆运动学规律可知:

(9)

(10)

式中:βcf—前车体质心等效侧偏角;βcr—后车体质心等效侧偏角;ωf—前车体转动角速度;ωr—后车体转动角速度。

将前车体的加速度分解为后车体的加速度与相对后车体的加速度的矢量和,即:

(11)

铰接轮式工程车辆变转向角转向行驶时,在车辆坐标系中需要考虑前后车体相对运动产生的科氏加速度。根据科氏加速度定义,前后车体科氏加速度为:

(12)

式中:vrr—后车体质心相对于转动系的相对速度;vrf—前车体质心相对于转动系的相对速度。

在任意转向角下,铰接轮式工程车辆的侧倾中心都与OfOr平行。以OfOr为参考系,可得前后车体科氏加速度垂直于OfOr的分量acrn、acfn:

(13)

式中:cf—前车体质心到前轴的距离在xf方向的投影长度;cr—后车体质心到后轴的距离在xr方向的投影长度。

通过以上运动学分析,笔者获得了前后车体的运动学关系,解算了铰接轮式工程车辆动力学建模所需的运动学参数。

1.3 车辆动力学模型

在倾角为φ的斜坡上,车辆前后车体的受力情况如图4所示。

图4 斜面上的铰接轮式工程车辆示意图Grx—后车体重力的纵向分量;Gry—后车体重力的横向分量;Gr—后车体重力;Grz—后车体重力垂直于斜面的分量;Grs—后车体重平行于斜面的分量;Fzrr—右后轮垂直载荷力;Fzrl—左后轮垂直载荷力

将前后车体重力如图4进行分解,可得:

(14)

式中:Gfx—前车体重力的纵向分量;Gfy—前车体重力的横向分量。

由车轮垂直载荷力与车辆重力垂直于斜面的分力平衡,可得:

Fzr+Fzl=(Gr+Gf)cosφ

(15)

式中:Gf—前车体重力;Fzl—左侧车轮垂直载荷力;Fzr—右车轮垂直载荷力。

根据动力学分析,可以得到重力和车轮垂直载荷力对OrOf上的力矩Lg、Lz:

(16)

(17)

式中:hf—前车体的质心高度;hr—后车体的质心高度;θp—OrOf的俯仰角。

在车轮侧偏角满足αt≤7°时,魔术公式能够准确反映轮胎的动力特性[13-15]。设轮胎的侧偏刚度为Ct,可得侧偏角与轮胎侧向力的简化公式如下:

(18)

式(18)还可转化为:

(19)

分别计算两个车体的惯性力,可得:

(20)

(21)

式中:Fifx—地面坐标系下前车体纵向惯性力;Fify—地面坐标系下前车体横向惯性力;Firx—地面坐标系下后车体纵向惯性力;Firy—地面坐标系下后车体横向惯性力;Finf—车辆坐标系下前车体在垂直于OfOr方向的惯性力;Finr—车辆坐标系下后车体在垂直于OfOr方向的惯性力。

在车辆OfOr参考系下,车体相对运动的科氏力和惯性力共同决定的侧倾力矩为:

Li=(mracrn+Firn)hr+(mracrn+Fifn)hr

(22)

根据达朗贝尔原理,考虑液压转向系统转向力矩,笔者建立车辆整体平动和前后车体转动的动力学平衡方程如下:

(23)

式中:Jfz—前车体对Zf方向的转动惯量;Jrz—后车体对Zr方向的转动惯量。

将上述动力学模型的微分方程转化为状态方程的形式:

R(x,u)=F(x,u)

(24)

X、R(x,u)与F(x,u)可整理为:

X=[vrxβcrβcfωrα]T

(25)

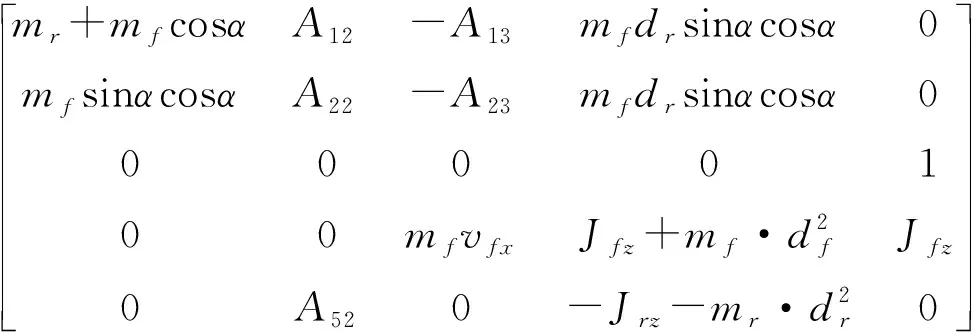
(26)

(27)

式中:

A12=mfvrxsinαcosα

(28)

A13=mf[vrxcosα+(ωdr-vrxβcr)sinα]sinα

(29)

A22=mfvrxsin2α+mrvrx

(30)

A23=mf[vrxcosα+(ωdr-vrxβcr)sinα]cosα

(31)

A52=-mrvrx·dr

(32)

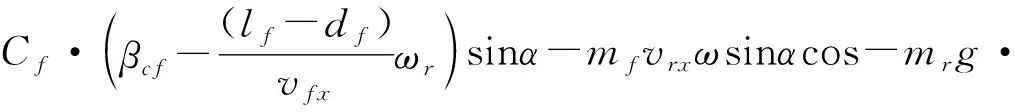
(33)

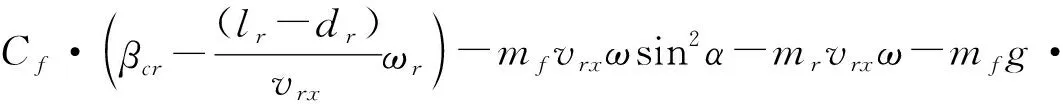
(34)

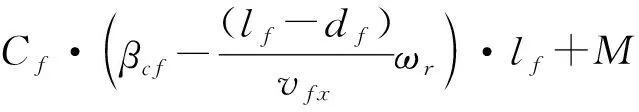
(35)

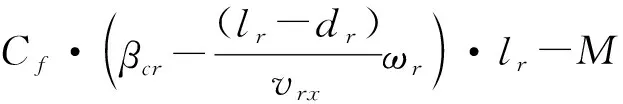
(36)

铰接轮式工程车辆的动力学模型最终可表述为:

(37)

1.4 动力学模型约束

在完成铰接轮式装载机动力学建模之后,需要为动力学模型添加合适的约束条件,包括车辆结构决定的约束条件、轮胎模型的有效性约束条件与侧倾失稳约束条件等。

铰接轮式装载机的稳定性是其动力学建模的主要研究内容之一,提高倾斜地面动态行驶过程中的抗侧倾稳定性对于铰接轮式装载机行驶安全具有重要意义。其侧倾失稳与各种因素有关,例如质心变化、车辆姿态变化、车辆整体运动和内部结构相对运动。

横向载荷转移率(LTR)通常被用于描述常规车辆的侧翻稳定性指标[16],其公式为:

(38)

LTR值在0～1之间变化,其中,LTR为0,代表两侧车轮载荷相等,车辆稳定行驶;LTR值为1,代表车辆载荷集中在一侧车轮,车辆即将侧倾[17,18]。然而在实际行驶过程中,装载机的轮胎垂直载荷力难以准确测量,同时,装载机车体变结构会引起侧倾中心与车辆相对位置变化,故LTR无法直接适用于铰接轮式装载机。

综合考虑倾斜地面下的车地相对位姿、车辆整体和前后车体运动、转动参考系下的科氏力等因素,笔者对铰接轮式装载机的侧倾动力学进行了分析,在前后轴中点线OfOr参考系中有:

Jfγf+Jrγr=Lz+Lg+Li

(39)

式中:Jf—前车体对OfOr的转动惯量;Jr—后车体对OfOr的转动惯量;γf—前车体对OfOr的角加速度;γr—前后车体对OfOr的角加速度。

Lz、Lg、Li由式(15,16,21)确定。通过转动惯量的合成原理和运动矢量叠加原理可知:

(40)

(41)

式中:Jfx—前车体纵向转动惯量;Jrx—后车体纵向转动惯量;γfx—前车体纵角加速度;γrx—后车体纵向角加速度;Jfy—前车体横向转动惯量;Jry—后车体横向转动惯量;Jfxy—前车体纵向和横向惯性积;Jrxy—后车体纵向和横向惯性积。

在车辆尚未侧翻时,其对于OfOr的角加速度为0,联立式(15～17,22,38～41),可获得铰接轮式装载机的横向载荷转移率(avLTR),即:

(42)

根据铰接轮式装载机的结构特点,结合车辆动力学模型中常用的失稳约束,以及轮胎模型的有效性范围,给出以下约束条件:

(43)

式中:γ—后车轴与后车体之间的夹角。

2 动力学模型实验及结果分析

为了验证动力学模型的有效性,基于搭建的铰接轮式装载机1 ∶4比例样机,笔者进行实验测试。比例样机由铝型材搭建框架,后轴中点与后车体铰接,以轮毂电机为驱动,前后车体铰接连接,通过电推杆实现转向控制;比例样机模型以实际铰接装载机的结构特征为参照,与实际车辆的相似性较高,能够满足其动力学实验的需求。

比例样机的构成如图5所示。

图5 比例样机及主要传感器

该样机通过转向推杆读取其伸长量,通过旋转编码器获得前后车体的转向角,通过轮速传感器获得车速,并利用后车体质心位置安装的IMU采集加速度、角速度和姿态等信息,利用IMU采集的姿态信息对加速度进行修正,去除三轴重力加速度分量获得比例样机的实际运动加速度,并根据IMU和GPS定位信息生成行驶轨迹。

比例样机搭载的主要传感器型号如表1所示。

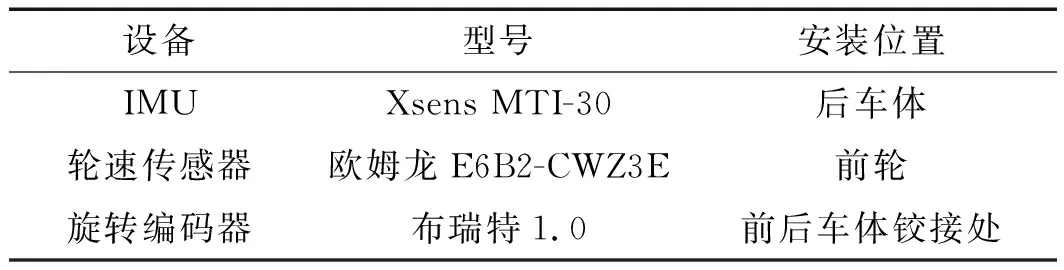
表1 比例样机搭载的主要传感器

车体主要参数如表2所示。

表2 比例样机模型主要参数

2.1 侧倾约束验证实验

针对铰接轮式装载机动力学模型的侧倾约束指标,需要对其有效性进行验证,而定转角加速实验和鱼钩工况实验是车辆最常用的横向稳定性实验。

因此,笔者利用搭建的比例样机进行非结构环境下定转向角加速侧倾实验和鱼钩工况侧倾实验,以记录下比例样机侧倾的时刻,并通过IMU、轮速传感器和旋转编码器记录动力学参数和转向角参数,代入式(42),解算侧倾前后的avLTR值,并进行对比分析。

在定转向角加速侧倾实验中,笔者控制转向角保持在30°,不断增加车速至一侧车轮离地,定转向角加速实验如图6所示。

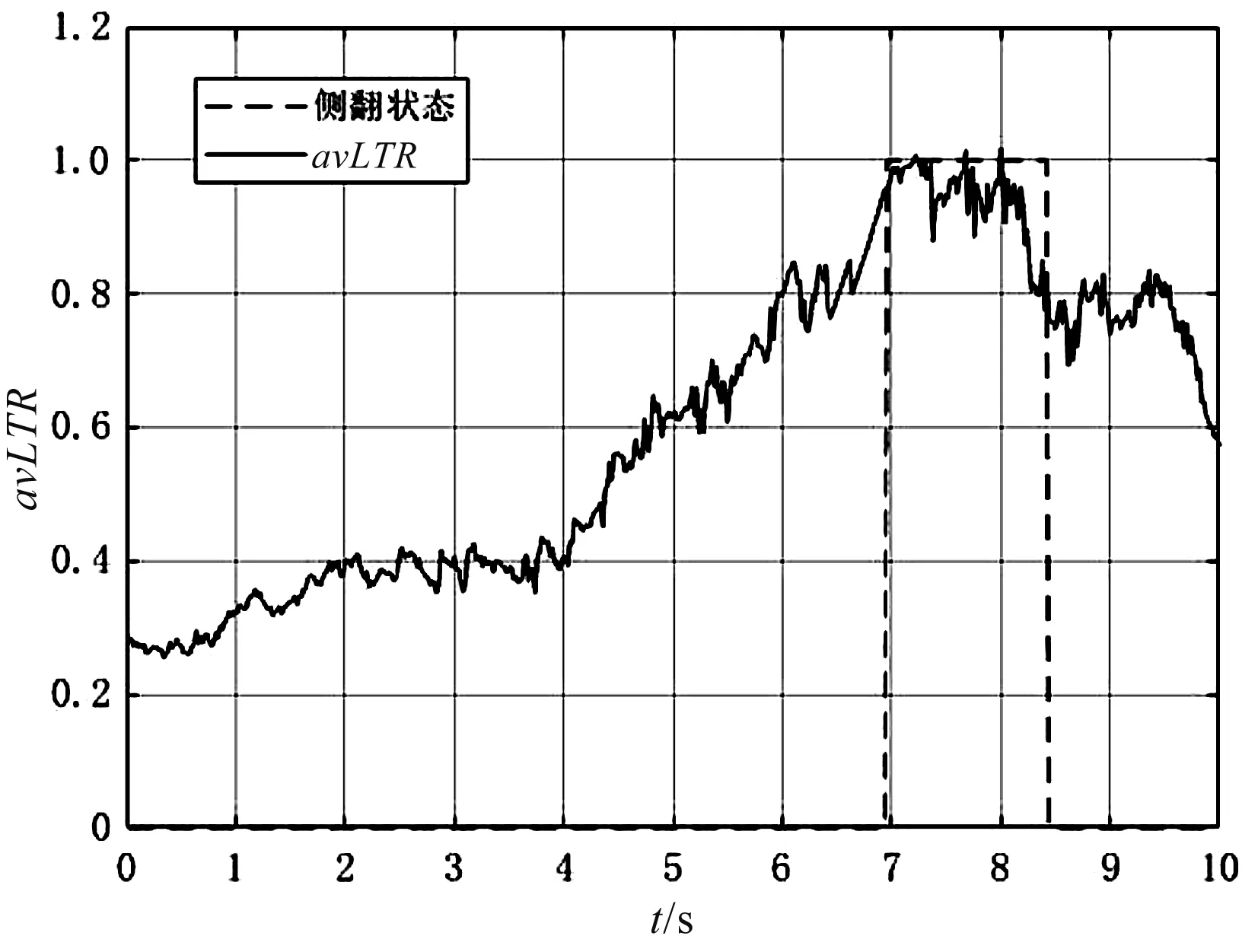
图6 定转向角加速侧倾实验

图6中,在5.76 s时,avLTR到达阈值0.7,在随后的6.92 s时刻,比例样机已经开始侧倾,单侧车轮已驶离地面,此时avLTR值为0.97,该结果与实际车辆侧翻状态吻合。

在鱼钩工况侧倾实验中,笔者控制比例样机进行加速行驶,然后控制电动推杆伸长,增大转向角至单侧车轮离地,鱼钩工况侧倾实验如图7所示。

由图7可得,avLTR在7.92 s时刻到达阈值0.7,

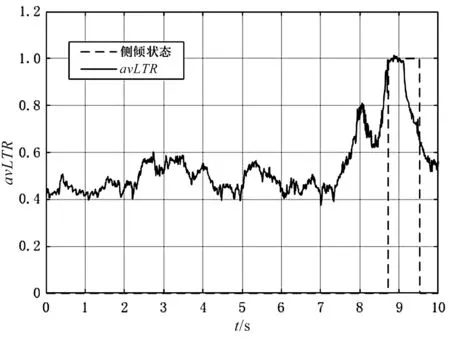
图7 鱼钩工况侧倾实验

但车辆并没有随即侧翻;随后笔者控制车辆继续加速行驶,比例样机在8.74 s时刻开始侧倾,此时avLTR值到达1,车辆已完全侧翻。

以上的定转向角加速侧倾和鱼钩工况侧倾实验结果表明:笔者提出的适用于铰接轮式装载机的avLTR可以较好地反映比例样机行驶过程中的横向稳定性。因此,通过合理地设置avLTR阈值,可以作为侧倾约束,防止样机进入侧倾危险工况。

实验中,比例样机的avLTR曲线存在比较明显的波动,这也反映了模型车在野外运动的实际情况。相比于比例样机,真实的铰接轮式装载机具有更大的质量和转动惯量,在相同的路面行驶获得的avLTR会更加稳定。

2.2 动力学模型验证实验

在动态行驶过程中,为了验证动力学模型的准确性,笔者进行了曲线行驶实验;设定后车体驱动轮速度设置为3 m/s,转向推杆伸长率设为0.03 m/s。

曲线行驶下实验结果与模型结果对比如图8所示。

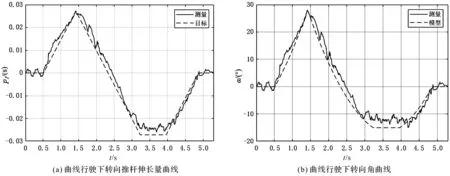
图8 曲线行驶下实验结果与模型结果对比

由图8(a～d)可知:在曲线行驶实验中,转向推杆伸长量先增大后减小,随后恢复到原长;转向角变化趋势与转向推杆伸长量变化基本一致;模型的横向加速度、曲率与实验结果保持较好跟踪趋势。该结果表明,该动力学模型能够有效地描述车辆的铰接转向与横向动力学参数特性。

由图8(b,e)可知:在推杆开始持续伸长后的0.9 s,比例样机并没有直接开始右转,而是先向左行驶,再向右行驶,这种转向迟滞现象是铰接轮式装载机独特转向机理引起的;在行驶初期阶段,电动推杆伸长推动前后车体相对旋转,给予前后车体相反方向的力偶矩,在该力偶矩作用下,车辆行驶速度小于液压转向速度,造成了前后车体转向迟滞现象,使得转向过渡处的模型误差较大。

笔者建立的动力学模型较好地仿真模拟了铰接轮式装载机转向迟滞现象,也证明了该动力学模型的有效性。

在实验中,转向角、横向加速度、曲率、车辆位置以50 Hz频率采样,通过统计采样时刻的测量值与模型值的误差,通过计算可得到上述各项的误差分布,如图9所示。

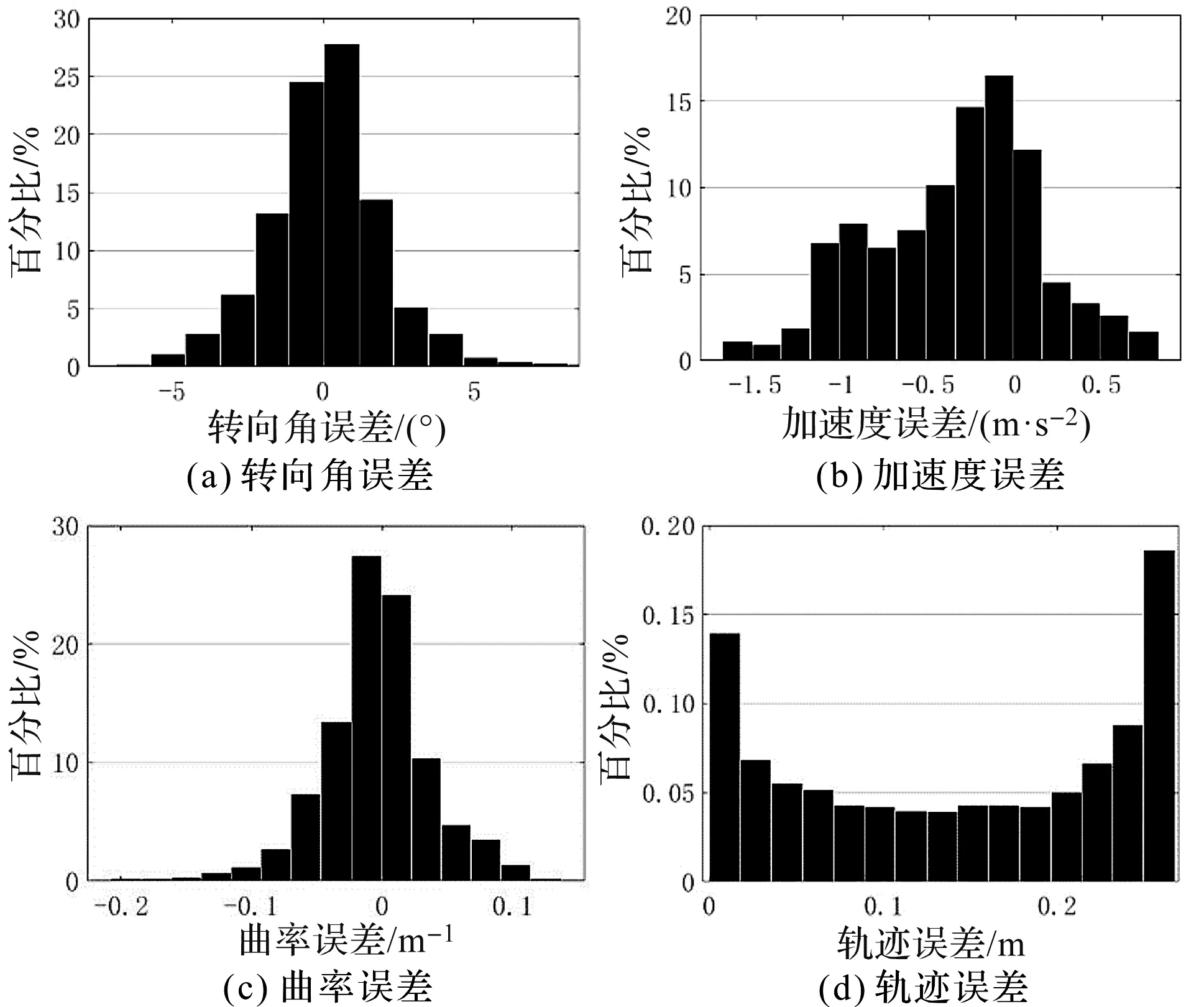
图9 曲线行驶实验误差分布直方图

图9中,通过采样点的误差值可以获得模型转向角、横向加速度、曲率与轨迹的均方根误差,其均方根误差分别为1.71°、0.89 m/s2、0.05 m-1、0.13 m;转向角、横向加速度、曲率的误差分布在零值附近,而行驶轨迹由于存在累计误差,在行驶初段轨迹误差较小,行驶一段时间后轨迹误差将逐渐变大,在误差分布直方图表现为误差在较大值中分布较多。

总体上,实验中的各项模型解算值与实际测试结果基本吻合。实验结果进一步表明,该动力学模型能够较好地描述铰接轮式装载机的横向动力学特性。

3 结束语

针对非结构环境工况下,铰接轮式装载机的横向动力学变化特性,笔者开展了相关动力学建模研究,利用达朗贝尔原理建立了铰接轮式装载机的动力学模型,分析了模型相关的约束条件,并通过搭建比例样机,对其进行了验证。

研究结果表明:

(1)所提出的侧翻约束指标avLTR能准确地反映非结构环境中,铰接轮式装载机的横向稳定性;对其设定合理的阈值,可将其作为动力学模型的侧翻约束条件;

(2)在非结构环境行驶过程中,所建立的动力学模型能够对车辆动力学变化特性进行准确的描述,同时可以较好地仿真模拟车辆的铰接转向迟滞现象。

该动力学模型的良好表现仅仅是在比例样机上得到了实验验证,而没有在实际大型非结构工况下的铰接轮式装载机上得到验证。因此,接下来的研究中,笔者将在铰接轮式装载机上进一步开展实车验证,以及进行动力学模型的应用研究。