基于导轨多激励关联的轿厢水平振动预测方法*

武 仪,萨日娜,,*,裘乐淼,张利春,张 静

(1.内蒙古工业大学 机械工程学院,内蒙古 呼和浩特 010051;2.浙江大学 机械工程学院,浙江 杭州 310027;3.康力电梯股份有限公司,江苏 苏州 215213)

0 引 言

高速电梯是高层建筑必不可少的运输设备。高速电梯的振动性能是决定电梯安全性和舒适性的关键因素。如何在设计阶段有效预测高速电梯的振动特性,对提高电梯产品设计方案稳健性具有重要意义。

国内外研究学者针对电梯振动预测问题进行了大量研究。这些研究主要包括振动建模、振动仿真、预测算法3个方面:

(1)振动建模方面。QIU L M等人[1]2-4提出了轿厢设计参数优化方法,建立了轿厢水平振动的二自由度动力学方程。ZHANG R J等人[2]考虑滚动导靴的非线性特性,建立了滚动导靴的非线性模型。LIU J等人[3]考虑气流和导向系统共同作用,建立了轿厢的水平振动动力学模型。WANG C等人[4]考虑了参数随机性,根据摄动理论分析了轿厢观测点的横向振动加速度响应。

(2)振动仿真方面。KAZUKI S等人[5]提出了一种导靴仿真模型,用以评估由导靴所产生的应力引起的电梯横向振动;并且将仿真结果应用于导轨结构参数的设计中。QIU L M[1]5、陈杰等人[6，7]研究了弯曲激励单独作用对轿厢水平振动的影响。郭天水[8]研究了弯曲激励、阶跃激励和失调激励叠加情况下,轿厢水平振动的响应。

(3)预测算法方面。主要研究成果有拟合方法和机器学习方法[9-18]。其中,拟合方法包括多项式拟合、最小二乘拟合、响应面拟合等;机器学习方法包括人工神经网络、支持向量机回归等。

以上研究对电梯振动预测研究具有重要参考价值。现有对轿厢水平振动的研究主要考虑的是导轨单因素激励[19-24]。然而引起高速电梯轿厢水平振动的激励因素有很多。导轨是电梯导向系统的重要部件。由于制造、安装误差等原因,导轨会存在弯曲、阶跃、失调等问题。这些因素之间的相互关联作用,也影响着轿厢的水平振动。例如导轨弯曲变形会引起导轨拼接处倾斜,进而导致导轨失调。导轨拼接处错位会导致导靴滚轮跳动,进而使导轨的受力不均匀,而且轿厢长时间在变载荷作用下运行,会导致导轨局部弯曲变形、表面磨损等问题的发生。

针对以上问题,笔者结合导靴-导轨接触模型,建立高速电梯轿厢二自由度水平振动等效动力学模型,考虑导轨多源激励关联性,并基于Dematel方法得出各激励的重要度;构建基于布谷鸟算法改进的支持向量机回归方法,建立轿厢水平振动预测模型,对比分析CS-SVR、SVR、RBF、BP、GA-BP预测结果,最后通过康力KLK2电梯样机进行对比实验。

1 轿厢水平振动模型

1.1 导靴-导轨接触模型

电梯导靴分为滑动导靴和滚动导靴。滑动导靴主要用于低速电梯,而滚动导靴主要用于高速和超高速电梯。导靴主要由滚轮、摇臂、弹簧、限位装置和靴座组成;滚轮主要由金属或尼龙材质的轮毂和外圈硬质橡胶组成,其弹性元件主要为弹簧和滚轮外圈橡胶。

由机械动力学理论可知,质量弹性元件同时具有惯性、弹性和阻尼3种特性,而相对于轿厢系统的质量,导靴的质量非常小,为了便于分析,此处忽略导靴的质量。由于滚轮橡胶的刚度远大于弹簧的刚度,工作时导轮橡胶形变较小,笔者在研究和建模中将其视为刚体,不考虑导轮和导轨间的弹性接触关系;将导靴简化为弹簧阻尼系统,建立导靴-导轨接触振动模型。

1.2 轿厢水平振动建模

在进行轿厢水平振动分析之前,需要建立轿厢振动坐标系。笔者以轿厢质心为原点,以平行于轿厢门运动方向为X轴,以平行于轿厢侧向为Y轴,以轿厢提升方向为Z轴,建立空间直角坐标系。

轿厢振动坐标系如图1所示。

图1 轿厢振动坐标系

按空间维度划分,电梯振动通常分为横、纵、侧3个方向。图1中,横向振动对应平行于X轴方向的移动和绕着Y轴的转动,侧向振动对应平行于Y轴方向的移动和绕着X轴的转动,纵向振动对应平行于Z轴方向的移动。此处,笔者主要研究的是由于导轨多源激励作用下引起的轿厢横向振动。

而实际上,电梯是非常复杂的机电一体化设备,影响电梯振动的因素也非常复杂。为了便于分析计算,此处做出3项假设:(1)将轿厢和轿厢架视为整体,忽略细节影响;(2)将4只导靴视为弹簧阻尼系统,且4只导靴的等效刚度及等效阻尼均相等;(3)忽略滚轮橡胶变形对轿厢振动的影响[1]4。

轿厢二自由度水平振动等效动力学模型如图2所示。

图2 轿厢二自由度水平振动等效动力学模型x—轿厢水平振动位移(以向右为正方向);θ—轿厢绕其质心转动的角位移(以逆时针为正方向);xa,xb,xc,xd—4只导靴的位移激励(以向右为正方向);v—电梯运行速度;m—轿厢及轿厢架的质量;J—轿厢及轿厢架的转动惯量;ka,kb,kc,kd—4只导靴的等效刚度;ca,cb,cc,cd—4只导靴的等效阻尼;la—导靴a和c到轿厢质心的垂直距离;lb—导靴b和d到轿厢质心的垂直距离

下面对动力学模型进行分析。根据牛顿第二定律,电梯轿厢水平振动的动力学方程为:

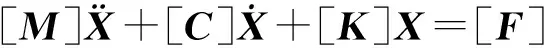
(1)

根据牛顿第二定律、振动基本原理、弹性元件和阻尼元件的动力学特性,可得到高速电梯水平振动动力学系统微分方程:

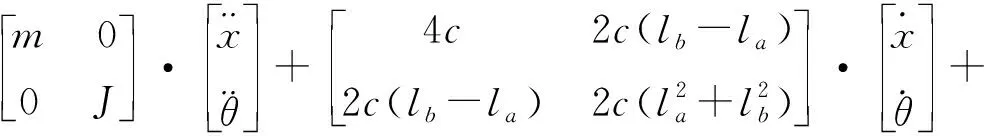
(2)

2 导轨多源激励关联性分析

2.1 导轨多源激励因素分析

电梯导向系统的核心部件是导轨和导靴,其主要功能是限制轿厢与对重的运动自由度,使轿厢与对重只能沿着导轨铅垂线作升降运动。导轨本身的安装缺陷,如导轨对中误差、导轨垂直度误差、导轨接头不够平整、轨距在全高上误差过大、导轨支架松动、导轨表面粗糙不平和导轮缺陷等,均可能引起轿厢运行过程中产生水平振动。

综合考虑各种因素,笔者将导轨激励抽象为3种典型的激励因素:失调激励、弯曲激励和阶跃激励。

导轨多源激励因素分析结果如表1所示。

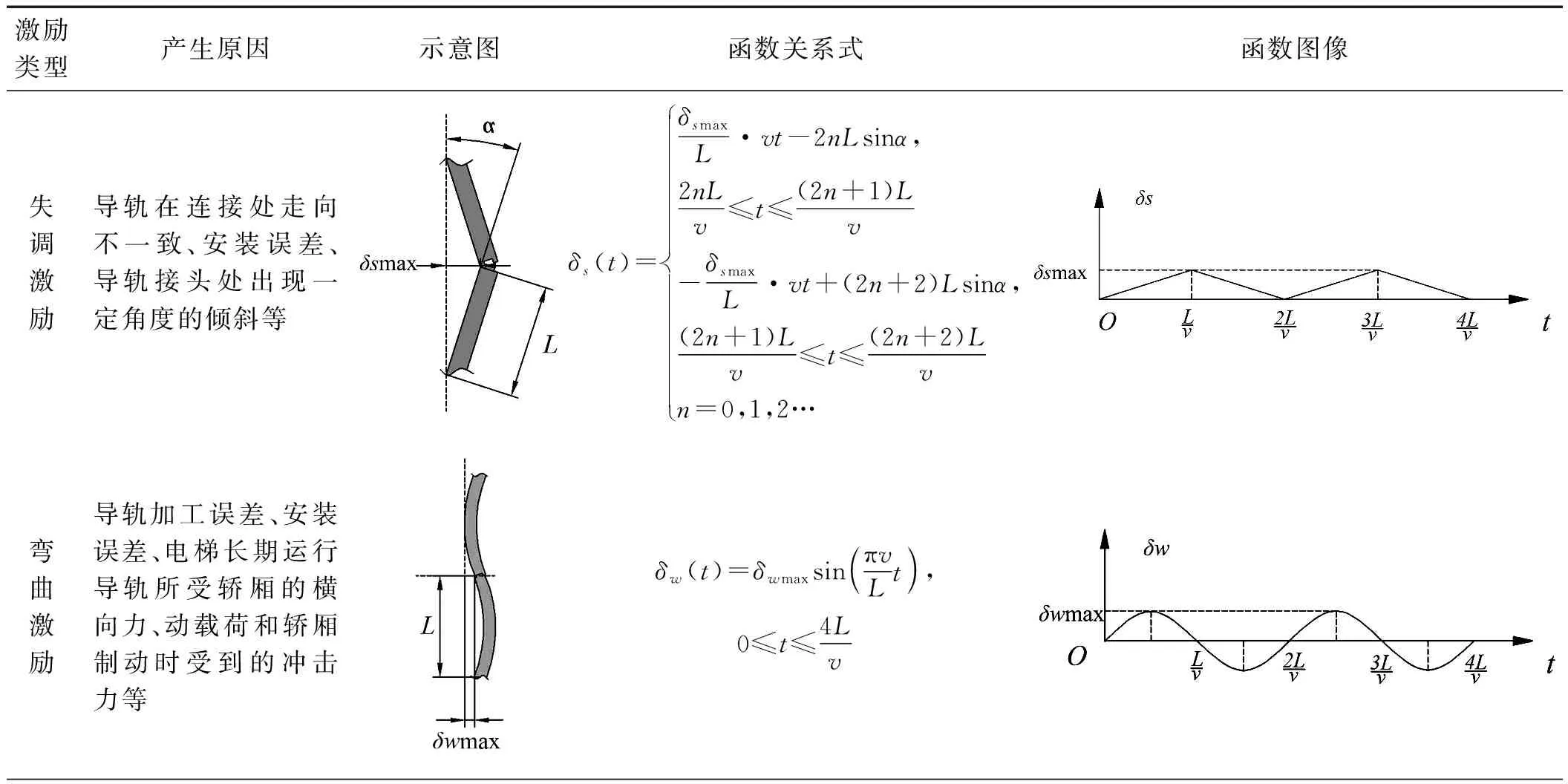
表1 导轨多源激励因素分析结果

续表

2.2 导轨多源激励采样

首先,笔者进行单独激励下的振动仿真,分析每种激励单独作用下轿厢水平振动响应;然后,考虑所有激励关联性,进行总体仿真分析。此处以电梯经过8根导轨的时间作为仿真总时长,单根导轨长为5 m,电梯运行速度为4 m/s,仿真总时长为10 s。由于左右两根导轨对导靴的激励程度完全一致,导靴a、c的激励信号相同,导靴b、d的激励信号相同;上、下两导靴间距为2.2 m,通过计算可以得出同侧导靴激励之间的时间间隔为0.55 s。

激励输入图像如图3所示。

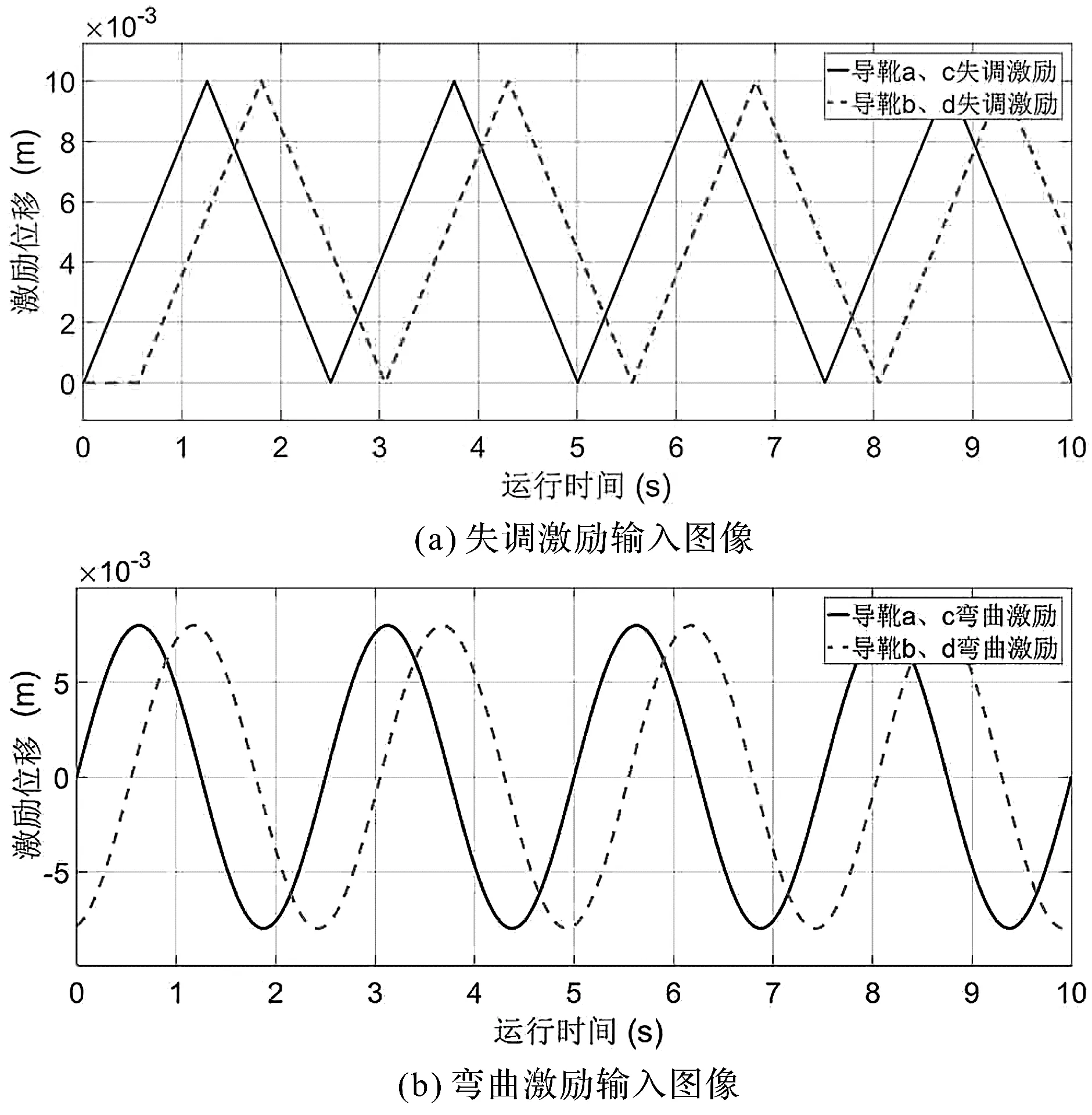
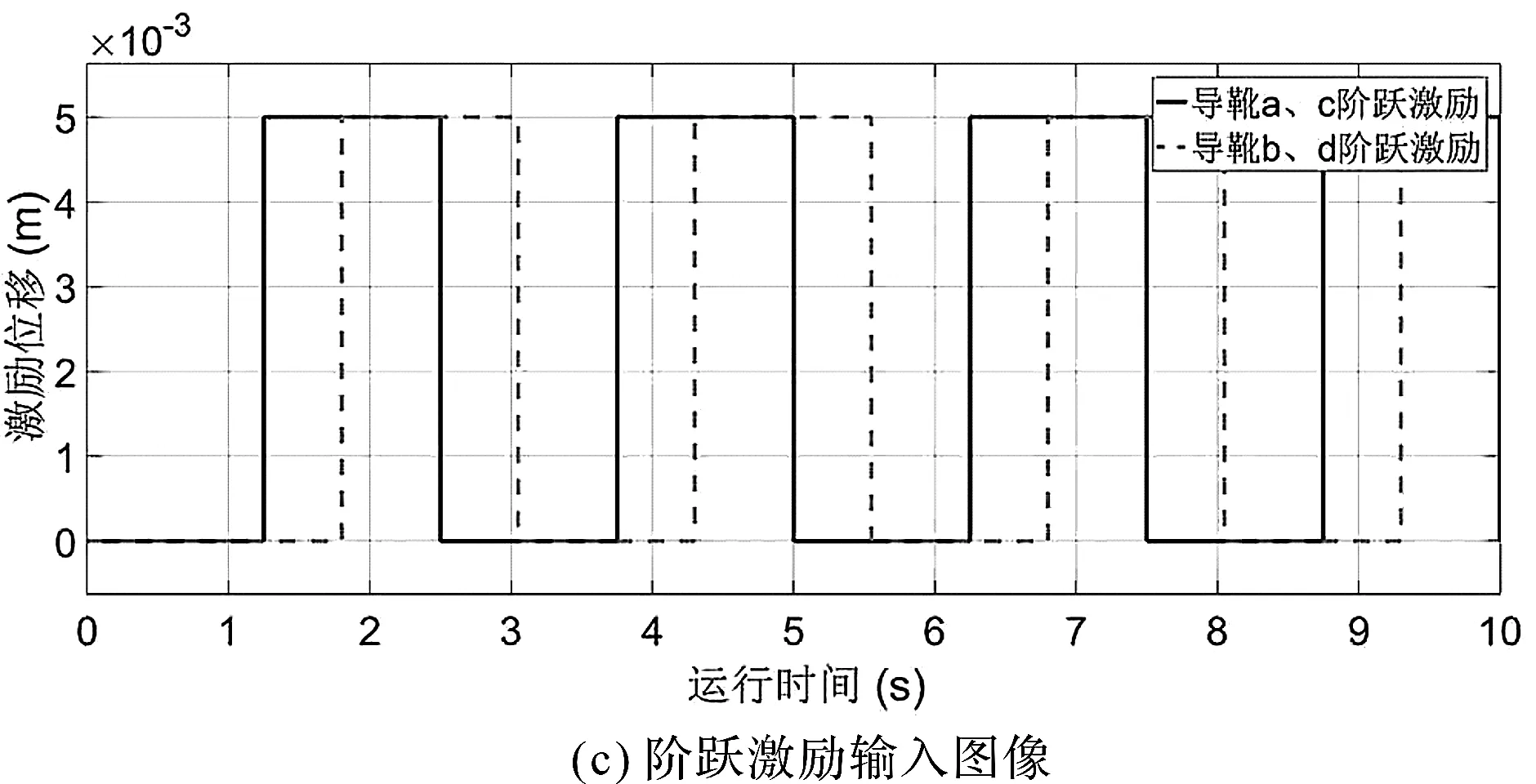
图3 激励输入图像

笔者以导靴a、c为标准,计算各激励直接影响矩阵,将上述导轨各激励输入进行离散化,分别取每种激励1 s～9 s的9个时刻位移绝对值,组成直接影响矩阵。例如,失调激励1 s、2 s、3 s的3个时刻激励位移分别为0.008 m、0.004 m、0.004 m,作为失调激励直接影响矩阵B1的第1行;4 s、5 s、6 s的3个时刻激励位移分别为0.008 m、0 m、0.008 m,作为失调激励直接影响矩阵B1的第2行;7 s、8 s、9 s的3个时刻激励位移分别为0.004 m、0.004 m、0.008 m,作为失调激励直接影响矩阵B1的第3行。弯曲激励和阶跃激励同理。

最后，为了便于计算,笔者将各数值整体扩大1 000倍,得到各激励直接影响矩阵Bk(k=1,2,3):

(3)

(4)

(5)

式中:B1—失调激励直接影响矩阵;B2—弯曲激励直接影响矩阵;B3—阶跃激励直接影响矩阵。

2.3 导轨多源激励关联性分析

Dematel方法是运用图论与矩阵工具进行系统要素分析的方法,是分析特征关联性的有效工具。采用Dematel方法计算各激励重要度过程如下:

(1)将各激励数据离散化,得到各个激励直接影响矩阵Bk=(bij)n×n,(k=1,2,3)。

(2)将直接影响矩阵Bk做归一化处理,得到矩阵Mk(k=1,2,3):

(6)

(3)计算出综合影响矩阵Xk(k=1,2,3):

Xk=(xij)n×n=Mk(I-Mk)-1

(7)

式中:(I-Mk)-1—矩阵(I-Mk)的逆矩阵;I—单位矩阵。

(4)根据综合影响矩阵,计算出各个属性的中心度a以及原因度b:

(8)

(5)确定各激励的重要度:

(9)

式中:h1—失调激励重要度;h2—弯曲激励重要度;h3—阶跃激励重要度。

3 CS-SVR轿厢水平振动预测

3.1 水平振动预测模型

虽然采用SVR方法进行非线性函数拟合的效果很好,但是需要调节惩罚因子C和RBF核参数γ,才能得到较好的精度。传统SVR模型采用网格遍历和交叉验证的方法,对参数C和γ进行寻优搜索。由于网格遍历方法寻优速度慢且效率低,当参数范围较大时,无法保证寻优速度和精度。基于此,笔者采用布谷鸟算法改进支持向量机回归。

CS-SVR振动预测模型如图4所示。

图4 CS-SVR振动预测模型

3.2 CS-SVR模型预测步骤

布谷鸟搜索算法具有随机搜索路径优和寻优能力强的特点[25],采用CS算法优化SVR参数寻优过程,可以有效避免过拟合和欠拟合状态的发生,并且提高寻优效率。

CS-SVR模型预测步骤如下所示:

(1)仿真得到轿厢水平振动响应样本数据,进行归一化处理,划分训练集和测试集;

(2)设定参数C和γ的取值范围为0.01～100,设定CS算法的迭代次数为50次,鸟巢个数为20个,设定概率Pa=0.25;

(3)随机产生20个鸟巢并初始化,以当前鸟巢对应的参数C和γ训练SVR模型,计算SVR平均均方误差,找到目前最优的鸟巢位置,即最低的平均均方误差;

(4)保留上一代最优鸟巢位置,并进行Levy飞行更新一组鸟巢位置,使用新的C和γ参数值训练SVR模型,计算每个鸟巢的平均均方误差;

(5)判断新鸟巢的平均均方误差是否低于旧鸟巢的平均均方误差,若不低于,则保留旧鸟巢;若低于,则使用新鸟巢代替旧鸟巢,得到一组较优的鸟巢位置;

(6)使用随机数r与Pa进行比较,判断是否需要更新鸟巢位置。如果r>Pa,则保留上一代中被发现概率较小的鸟巢,并对被发现概率较大的鸟巢进行位置更新,计算新鸟巢的平均均方误差,并且与旧鸟巢的平均均方误差进行比较,用较优的鸟巢位置代替差的位置,得到一组最优的鸟巢位置;如果r≤Pa,则保留上一代鸟巢位置;

(7)判断算法是否达到迭代次数,若未达到,则返回步骤(4)继续寻优搜索;若达到,则停止搜索,并输出全局最低平均均方误差对应的最优鸟巢;

(8)提取最优鸟巢所对应的最优参数C和γ,设置为SVR模型参数;

(9)使用训练集数据对SVR模型进行训练;

(10)使用测试集数据对SVR模型进行测试,将数据反归一化,计算出模型一系列的评价指标值。

高速电梯水平振动预测总流程如图5所示。

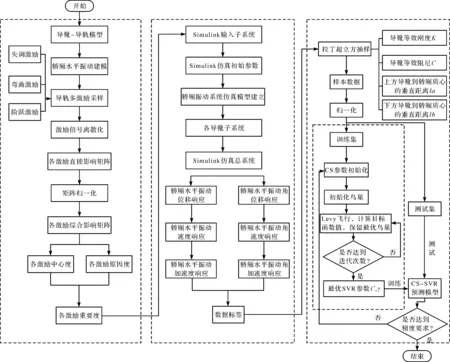
图5 高速电梯水平振动预测总流程

4 实验验证

4.1 轿厢水平振动特性仿真分析

笔者采用康力KLK2型高速电梯进行实验验证。KLK2型高速电梯主要参数如表2所示。

表2 KLK2型高速电梯主要参数

4.1.1 单因素激励作用下轿厢水平振动位移响应分析

为了便于对比分析,笔者将各激励单独作用下轿厢水平振动响应绘制在一张图中。各激励单独作用下轿厢水平振动位移响应如图6所示。

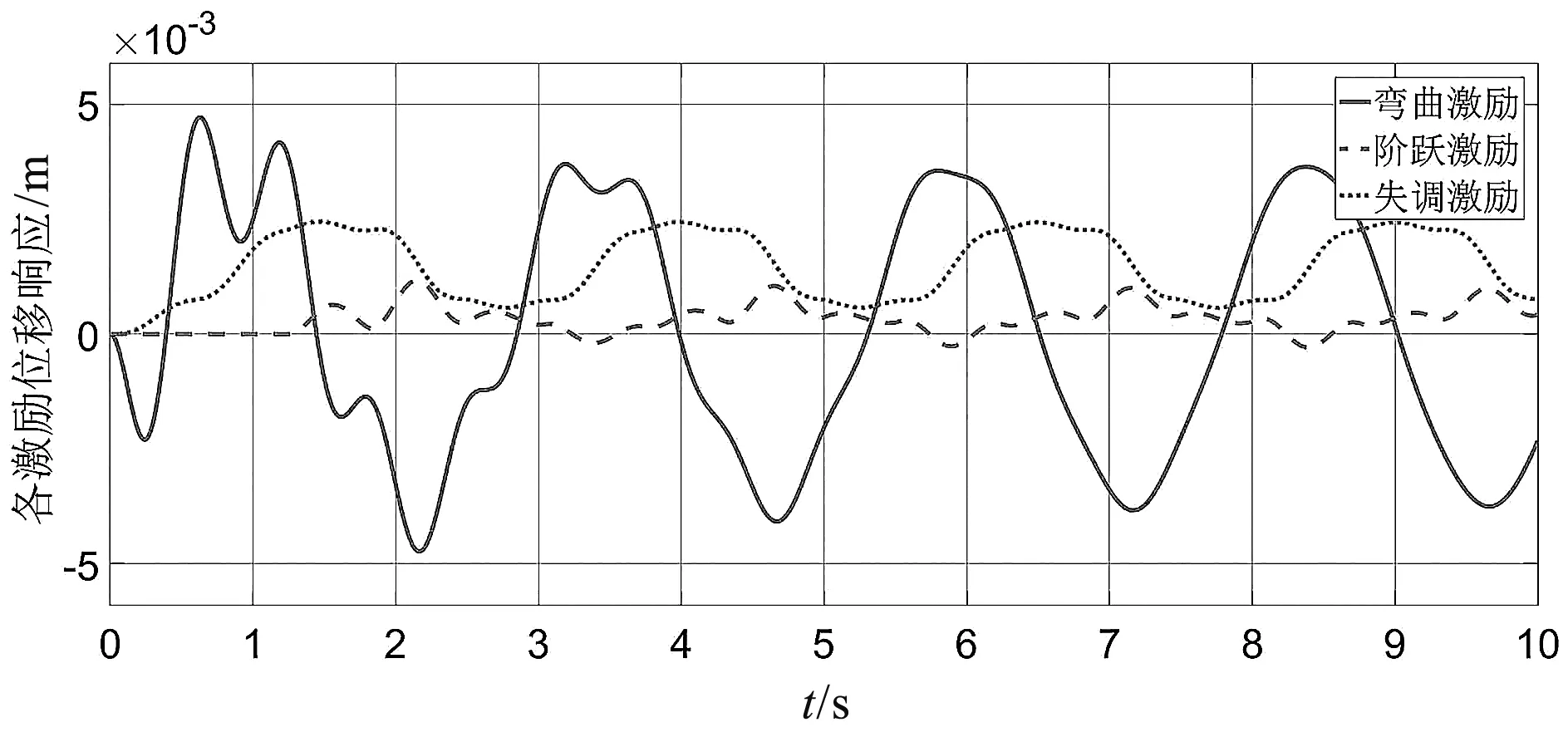
图6 各激励单独作用下轿厢水平振动位移响应

由图6可知:弯曲激励对轿厢水平振动位移影响最大,失调激励次之,而阶跃激励对轿厢水平振动位移影响较小。

各激励单独作用下轿厢水平振动速度响应如图7所示。

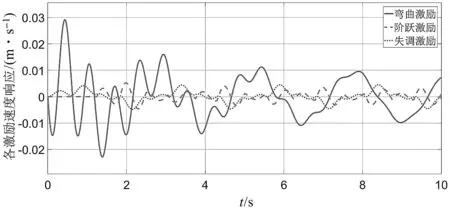
图7 各激励单独作用下轿厢水平振动速度响应

由图7可知:弯曲激励对轿厢水平振动速度峰值影响较大,而另外两种激励对轿厢水平振动速度变化频率影响更大。

各激励单独作用下轿厢水平振动加速度响应如图8所示。

图8 各激励单独作用下轿厢水平振动加速度响应

由图8可知:弯曲激励在运行前3 s内对轿厢水平振动加速度幅度影响较大,之后趋于稳定。由于激励输入图像变化频率较大,阶跃与失调激励对轿厢水平振动加速度变化频率的影响较大。

4.1.2 多源激励关联轿厢水平振动特性分析

多源激励耦合输入如图9所示。

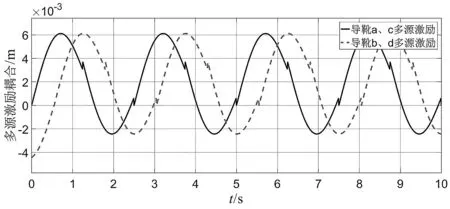
图9 多源激励耦合输入

笔者综合考虑多源激励关联性之间的影响,由前述Dematel方法计算出各激励的重要度,得到多源激励耦合输入,之后进行多源激励耦合振动仿真。

多源激励关联轿厢水平振动响应如图10所示。

图10 多源激励关联轿厢水平振动响应

由图10可知:轿厢的水平振动位移变化较为规律,变化过程中存在一些波动,波动范围为-2×10-3m～7×10-3m;轿厢水平振动速度在前2 s内峰值较大,大约在-0.02 m/s～0.03 m/s之间波动,之后趋于平缓。轿厢水平动加速度同样在前2 s内峰值较大,大约在-0.22 m/s2～0.23 m/s2之间波动,之后逐渐趋于稳定。

同理,多源激励关联轿厢水平转动响应如图11所示。

图11 多源激励关联轿厢水平转动响应

由图11可知:轿厢的水平振动角位移变化趋势与位移变化相似,同样在变化过程中存在一些波动,波动范围为-3.8×10-3rad～2.5×10-3rad;轿厢水平振动角速度在前2 s内变化较为剧烈,大约在-0.017 rad/s～0.016 rad/s之间波动,之后趋于稳定;轿厢水平振动角加速度在前3 s内变化剧烈,在-0.14 rad/s2～0.15 rad/s2之间波动,之后逐渐趋于稳定。

4.2 振动响应样本数据准备

拉丁超立方抽样方法能够有效地填充样本空间,抽取较少样本就可以获得较高计算精度。笔者将影响高速电梯水平振动的关键参数(导靴等效刚度、导靴等效阻尼、上方导靴到轿厢质心的垂直距离、下方导靴到轿厢质心的垂直距离)作为预测模型输入参数,其余参数固定不变,使用MATLAB编程,进行拉丁超立方抽样,得到220组随机样本。

笔者将水平振动加速度峰值和水平振动角加速度峰值作为输出参数,将Simulink仿真得到的数据作为预测模型训练数据和测试数据;随机选取20组样本作为测试数据,剩余的200组样本作为训练数据。

部分振动响应样本数据如表3所示。

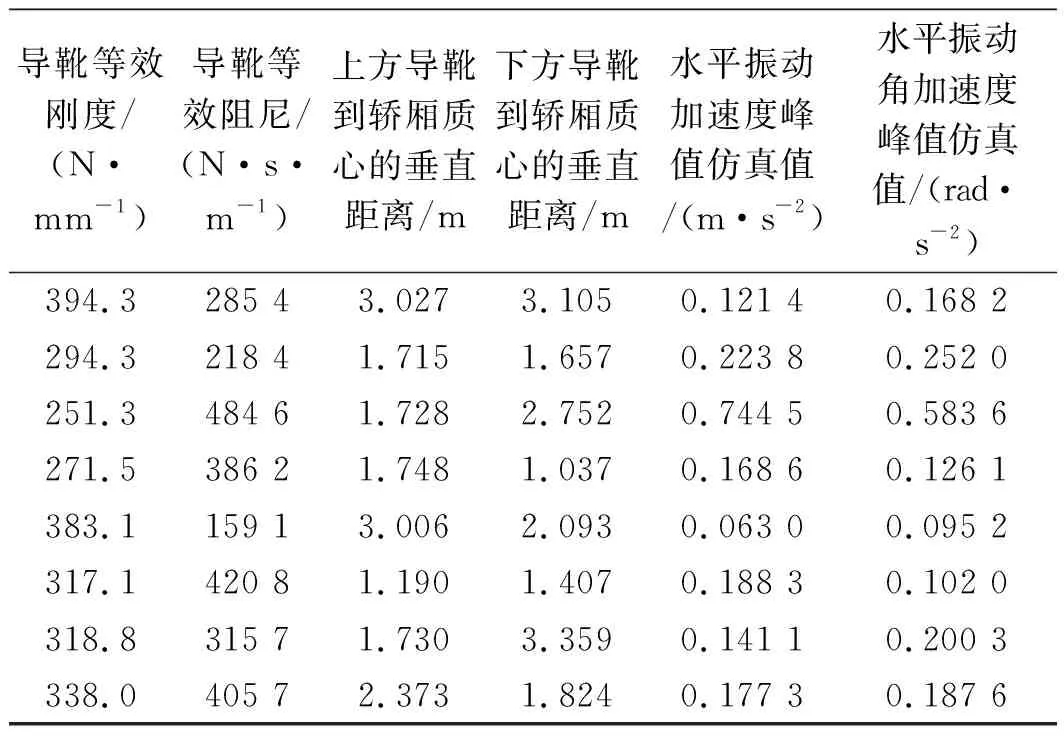
表3 部分振动响应样本数据

由于各个变量并不处于同一个数量级,需要采用归一化操作后进行模型训练,同时为了便于对比,预测值需要反归一化处理后,再进行对比分析。

4.3 预测模型训练

笔者使用200组训练集数据训练CS-SVR模型,并重复若干次实验,选取最优的参数C值为1.74,γ值为0.27。

SVR优化参数如表4所示。

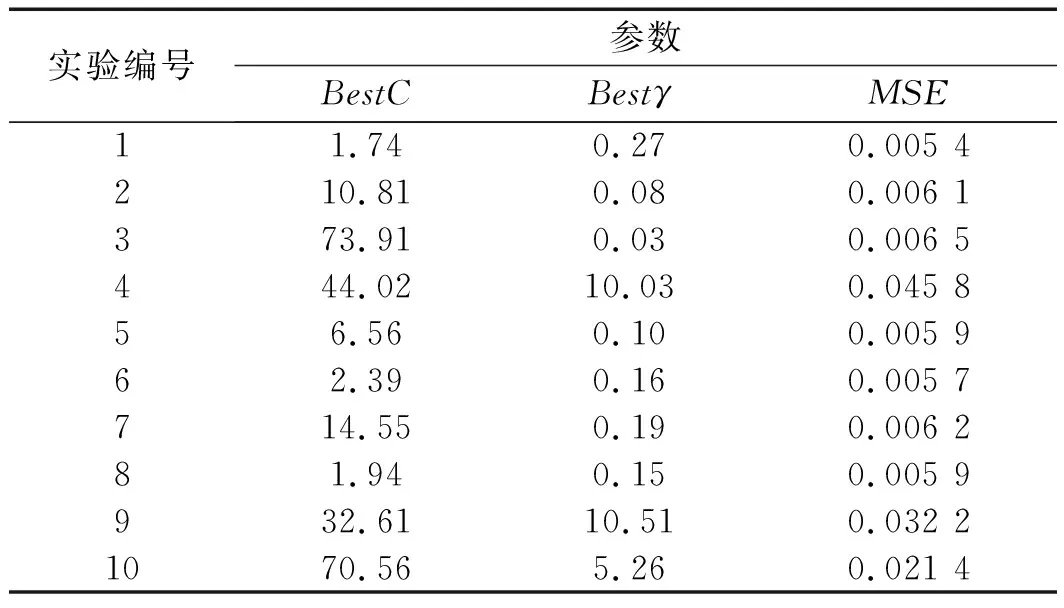
表4 SVR优化参数

4.4 讨论

4.4.1 导轨多源激励关联性结果分析

考虑各激励之间关联性,笔者采用Dematel方法计算出各激励的中心度和原因度,再由中心度和原因度计算出各激励重要度,最终计算结果为:失调激励重要度h1=0.300 7,弯曲激励重要度h2=0.564 1,阶跃激励重要度h3=0.135 2。

4.4.2 仿真值与预测值的对比

网络训练完成之后,笔者使用测试集数据测试各个模型的预测效果。

仿真值与预测值对比如图12所示。

图12 仿真值与预测值对比

4.4.3 预测方法性能对比分析

笔者采用决定系数、均方误差、平均相对误差和最大相对误差评价各预测方法性能。

预测方法性能对比分析如表5所示。

表5 预测方法性能对比分析

从均方误差的角度可以得出:CS-SVR预测模型均方误差最小,其次是传统SVR模型和遗传算法优化的BP神经网络模型GA-BP,而均方误差最大的模型是传统的BP神经网络模型;从决定系数的角度可以得出:CS-SVR预测模型的决定系数最大,说明CS-SVR预测模型对样本数据拟合效果较好,且没有发生过拟合现象。CS-SVR预测模型平均相对误差最小,且最大相对误差也最小。

结合各项指标得出:CS-SVR预测模型预测效果最优,更适用于对高速电梯水平振动进行预测。

4.4.4 KLK2型康力高速电梯样机振动性能实验

为了验证本文所提仿真与预测方法的准确性,笔者使用康力企业电梯实验塔,对KLK2型号高速电梯样机进行了实验,使用PMT EVA-625分析仪得到了该高速电梯实际水平振动响应。

KLK2样机实验与本文方法结果对比如表6所示。

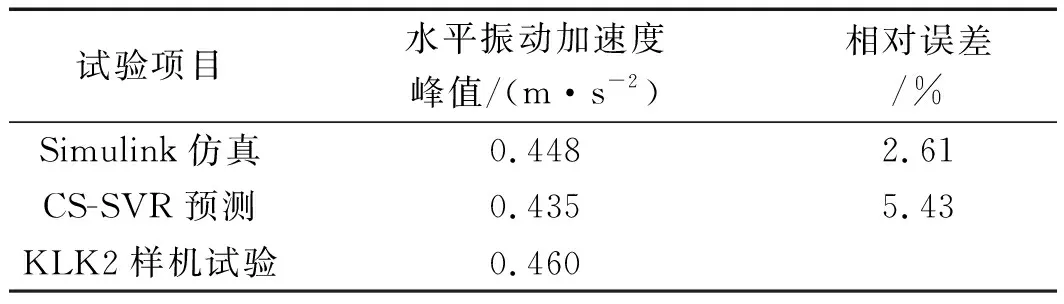
表6 KLK2样机实验与本文方法结果对比

表6显示:Simulink仿真与KLK2样机实验相比误差约为2.61%,本文所提CS-SVR预测结果与Simulink仿真相比误差约为2.90%,CS-SVR预测结果与KLK2样机实验相比误差约为5.43%。

由于实验过程中存在安装误差和测量误差,仿真误差与预测误差在可接受的范围之内。

5 结束语

由于高速电梯导轨多源激励存在关联性和在多源激励耦合作用下引起轿厢水平振动的问题,笔者提出了基于导轨多激励关联的轿厢水平振动预测方法,进行了以下研究工作,并得出以下结论:

(1)分析了高速电梯导轨对轿厢水平振动的多源激励影响因素,通过Dematel方法对导轨多源激励进行了关联性分析,得到了导轨多源激励关联重要度;结果表明,弯曲激励重要度较大,阶跃激励较小;

(2)使用仿真与机器学习相结合的方法,建立了CS-SVR、SVR、RBF、BP、GA-BP预测模型,并进行了对比实验;采用决定系数、均方误差、平均相对误差和最大相对误差,对预测模型进行了评价;结果表明,CS-SVR模型预测效果最优;

(3)通过康力电梯样机进行了对比实验,验证了本文所提方法的有效性。

本文仅对高速电梯振动预测方面进行研究,下一步拟开展高速电梯振动控制方面的研究。