近壁圆柱绕流尾流的特性*
李姜华,王伯福†,邱翔,周全††,刘宇陆
①上海大学 力学与工程科学学院/上海市应用数学和力学研究所,上海 200072;②上海应用技术大学 理学院,上海 201400
近壁圆柱绕流运动普遍存在于许多工程领域中。在河床底部和海底附近的输油管道或光缆等受横流作用会产生大尺度涡脱落,从而产生冲刷河床底部的现象;飞机着陆和起飞阶段的尾涡与地面跑道相互作用会影响飞机的升力和阻力;涡轮机械中上游转子叶片尾迹对下游定子叶片流场产生影响;航空工程中大型客机机翼前缘缝翼与主翼相互影响;海洋工程中近海底潜艇在洋流作用下与底壁相互作用会留下被监测的痕迹:这些实际工程问题都可以简化成近壁面圆柱绕流的物理模型[1-4]。当圆柱靠近壁面时,圆柱尾流与壁面边界层会产生复杂的相互作用,研究其相互作用的复杂机理对实际工业和工程应用中进行管道形状优化、机翼或叶片设计以提高传热传质效率和减小壁面摩擦阻力等具有重要意义。
单圆柱绕流是一个经典的流体力学问题[5-10]。圆柱放置在远离壁面的位置,即不受壁面影响时,其尾流卡门涡街呈周期性的旋转涡对,在向下游演化的过程中逐渐衰减、耗散并最终湮灭。当圆柱放置在壁面附近时,由于壁面边界的存在,圆柱绕流尾流涡结构脱落的周期性和规律性将受到破坏,这将区别于单圆柱绕流的尾流特性。图1为近壁圆柱绕流示意图[11],其中圆柱直径记为D,圆柱下沿至壁面的距离(即间隙大小)为G,边界层厚度为δ,来流速度为U。需要指出的是,这里的边界层厚度δ一般为相同雷诺数下未放置圆柱的平板边界层厚度。

图1 近壁面圆柱绕流示意图[11]
近壁圆柱绕流时,不仅圆柱尾流会受到壁面的影响,壁面边界层也会受到圆柱尾流的影响。大尺度的圆柱尾流结构与边界层相互作用时,会在边界层中产生新的湍流结构和流动现象。近壁圆柱绕流尾涡在壁面产生逆压梯度,可视为固壁黏性无法进一步阻止旋涡诱导作用的结果[12],致使边界层分离,继而产生二次涡结构[13]。对二维非定常不可压N-S方程求解,结果显示:从壁面脱落的二次涡围绕尾涡旋转,其后新的三次涡乃至四次涡会相继产生并绕尾涡旋转,引起尾涡运动轨迹的上下波动[14]。Li等人[15]通过数值模拟得到的流场具有相同的流动现象。Pan等人[16]研究发现,近壁圆柱绕流尾涡在壁面附近诱导产生的二次涡三维失稳形成发卡涡结构,致使边界层发生转捩,最终边界层发展为湍流边界层。此时的湍流边界层中存在大量壁湍流的典型湍流结构,包括发卡涡、发卡涡包和高低速条带等[16-19]。壁湍流中的湍流结构又受到壁面距离的影响而呈现层级现象[20]。壁湍流结构的能量因壁面剪切可以持续得到补充,因而具有更加复杂的湍流结构形态[20-23]。这又区别于单圆柱绕流产生的衰减的尾涡结构。
近壁圆柱绕流尾流与边界层的相互作用是工程中典型的复杂湍流类型之一,伴随着复杂的多尺度相互作用过程。由于相互作用产生的涡结构与圆柱绕流脱落的主涡的相互作用伴随着非常复杂的动量和能量的输运过程,这些复杂湍流结构的相互作用增加了湍流问题的复杂性。关注自由剪切和壁湍流两种不同类型剪切湍流的相互作用机制也提供了研究湍流机理的不同视角,而对其动力学行为的研究也有助于寻找优化的流动控制方案。本文回顾已有近壁圆柱绕流的研究结果,主要从边界层对圆柱涡脱落的影响和圆柱尾流对边界层的影响两大方面进行介绍。
1 边界层对圆柱涡脱落的影响
1.1 边界层厚度和间隙大小对圆柱涡脱落、升阻力的影响
单圆柱绕流在超过临界雷诺数时,圆柱上会发生规则的涡脱落,如图2所示,在圆柱后方形成卡门涡街。涡从圆柱脱落会导致圆柱周围局部压力变化,这样就形成了圆柱所受阻力和升力的脉动。记无量纲阻力系数、升力系数和涡脱落频率分别为CD、CL和St,这三个参数是工程应用中最关注的物理量。当圆柱位于壁面边界层附近时,边界层内的速度梯度和边界层的湍流特性对这些参数也有一定的影响[25]。

图2 单圆柱绕流可视化显示:(a)虚拟染色可视化;(b)Sadatoshi Thanda拍摄的烟迹可视化[24]
早期对此类问题的研究,主要方法是拉动圆柱运动,而流体是保持静止的[26],因此没有边界层的影响。随着研究的深入,研究者开始观察到了边界层厚度和间隙比(G/D)对圆柱涡脱落和圆柱升阻力的影响。Bearman和Zdravkovich[27]研究了边界层厚度为0.8D时的圆柱涡脱落情况,发现在间隙比大于0.3时,规则的涡脱落发生,St稳定于某个常数,不随G/D变化而变化,但是G/D小于0.3时,涡脱落受到抑制。在压力检测过程中,他们发现G/D小于0.6时,随着G/D的减小,圆柱基压的变化幅度迅速减小。对于小间隙比,前驻点会移动到壁面,从而产生一个稳定的平均升力。Grass等人[28]发现当间隙比小于2时,St随着间隙比减小而上升,他们认为下游边界层分离产生了自由射流,使得靠近壁面侧的圆柱尾流涡量被抵消,从而抑制了涡脱落。Zdravkovich[29]研究了CD随着不同边界层厚度的变化,结果表明:当圆柱位于边界层外时,阻力系数是个常数;圆柱进入边界层内时,CD随着间隙和边界层厚度之比下降而下降。Buresti[30]的研究结果显示升力大小在很大程度上依赖于间隙比的大小。
Lei等人[25]探究了边界层厚度和间隙比的影响,结果显示阻力系数受间隙变化的影响比受边界层厚度的影响更大。间隙比大于0.7,阻力系数随着间隙比增长几乎线性增长,而降低边界层厚度只会引起阻力系数的轻微上升。升力系数在较薄的边界层中随着间隙比的增大而逐渐减小,最终保持稳定,在这个过程中没有出现负值;但是在较厚的边界层中随着间隙比的增大,先减小至负值再逐渐增大,最终保持在零值附近。最近,Zhou等人[31]通过PIV(particle image velocimetry)实验研究了间隙比对圆柱涡脱落的影响,发现圆柱涡脱落频率对间隙比有很强的依赖。
近期文献对近壁圆柱绕流问题中圆柱受力情况的关注较少,更多关注的是圆柱尾流的流动现象。
1.2 间隙比和雷诺数变化对圆柱尾流的影响
由于壁面的存在,近壁面圆柱绕流尾流不同于图2所示的单圆柱绕流尾流,圆柱后方无法形成规则的卡门涡街。对于近壁面圆柱绕流流动,已有研究者在不同间隙比(G/D)和雷诺数(Re)下进行了大量的可视化研究。Bearman和Zdravkovich[27]考虑较薄边界层情况下G/D对圆柱尾流的影响,流动显示结果表明,小间隙比时,圆柱涡脱落被抑制,同时在圆柱上游和下游的壁面上形成了分离泡。
Cheng等人[32]对Re=500、0
Price等人[11]的近壁圆柱绕流流动可视化实验研究中考虑的参数为Re=1 200~4 960、G/D=0~2。主要结论如下:①对于非常小的间隙,G/D≤0.125,如图3(a)所示,圆柱下方的间隙流极弱甚至被抑制,圆柱上游和下游壁面边界层都发生了分离。虽然没有发现规则的涡脱落,但是在圆柱尾流中监测到了与圆柱上方剪切层相关的周期信号。②0.125
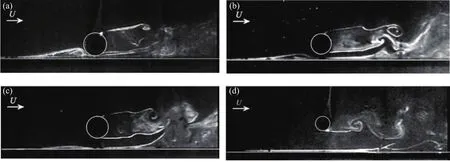
图3 不同间隙比近壁圆柱绕流实验拍摄结果[11]:(a) G/D=0.125;(b) G/D=0.25;(c) G/D=0.5;(d) G/D=1.5
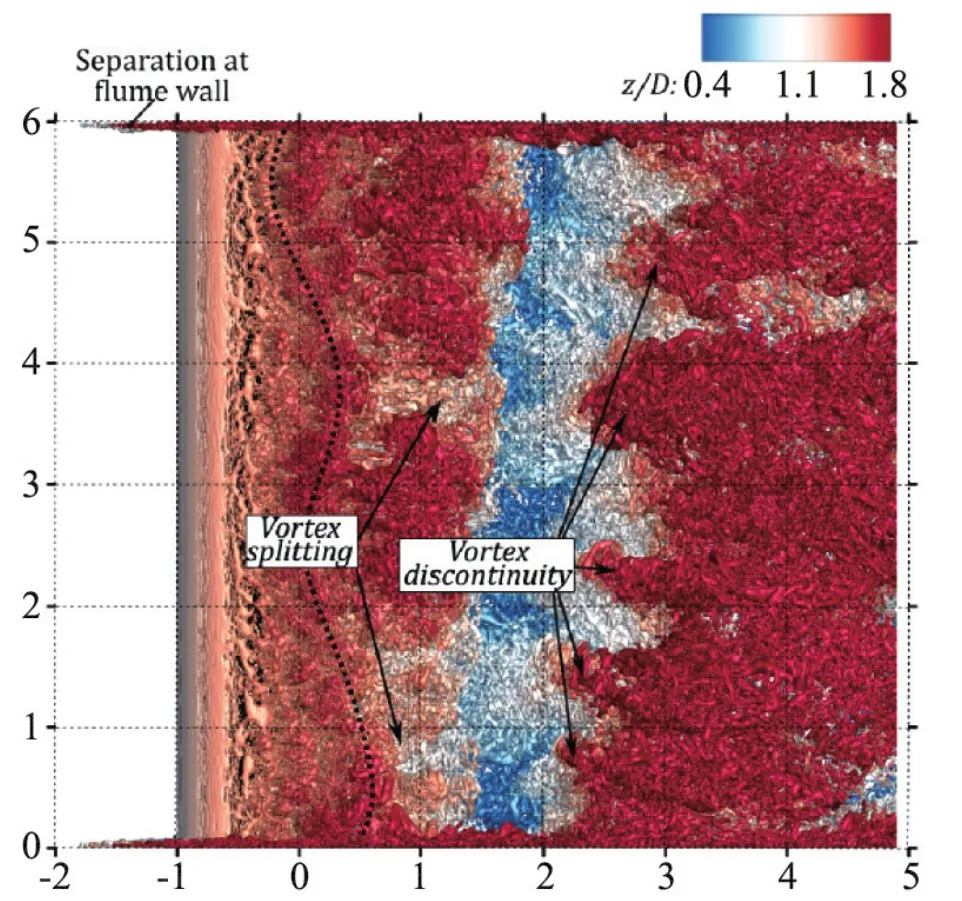
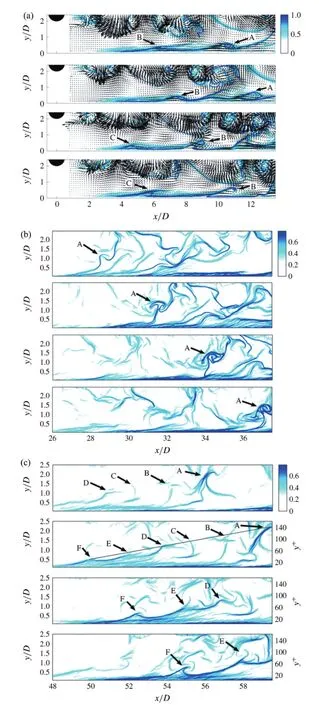
Wang等人[33]利用PIV研究了湍流边界层对圆柱尾流的影响,考虑参数为Re=1.2×104、0.1 He等人[37]开展了Re=1 072时不同间隙比(G/D=0~3)近壁圆柱绕流尾流的涡动力学实验研究。他们利用频谱分析得到G/D≥0.5的流场圆柱涡脱落频率,但是小间隙比时并未发现特征频率,而Price等人[11]利用流场中某些特定位置速度信号得到了小间隙比的特征频率。He等人[37]利用频谱分析得到的圆柱涡脱落频率进行了流场相位平均,涡识别结果如图4所示,圆柱上周期性地脱落涡,但是由于壁面的存在,圆柱尾流并未关于圆柱中心线对称分布。利用相位平均得到的流场,He等人也进行了涡结构追踪,如图5所示,在小间隙比情况下,圆柱尾涡轨迹存在交叉现象。这与Sarkar和Sarkar[34-35]的结果一致。He等人[37]同时使用虚拟染色剂的方法展示了涡结构演化(图6),发现在小间隙时,边界层对圆柱尾流的影响更大,边界层分离的涡结构会被卷进圆柱尾流,导致尾流中不同尺度结构的相互作用更加复杂,而在较大间隙比情况下并未发生此类现象。与图2相比,壁面的存在导致圆柱尾流出现明显的不对称性。 图4 G/D=1,不同相位角的流场涡结构识别[37]:(a) Φ=0;(b) Φ=π/2;(c) Φ=π;(d) Φ=3π/4。颜色代表涡量旋转方向 图5 不同间隙比的涡结构空间演化[37]:(a) G/D=0.5;(b) G/D=1.0;(c) G/D=1.5;(d) G/D=2.0。蓝色代表圆柱上侧脱落涡的涡核运动轨迹,红色代表圆柱下侧脱落涡的涡核运动轨迹,黑色代表二次涡的涡核运动轨迹 图6 不同间隙比下,虚拟染色剂显示的瞬时涡结构时空演化[37]:(a) G/D=0.5;(b) G/D=1.0;(c) G/D=2.0。蓝色代表圆柱上侧脱落涡结构,青色代表圆柱下侧脱落涡结构,红色代表二次涡结构;虚线圆标记的是圆柱尾流二次涡的相互作用及演化 Zhou等人[31]使用本征正交模态分解(The proper orthogonal decomposition, POD)低阶重构了PIV拍摄的流场并利用涡识别准则刻画了不同间隙比情况下圆柱涡和二次涡的演化过程。邱翔等人[36]实验研究了雷诺数对圆柱尾流与边界层相互作用的影响,发现随着雷诺数降低,流场中大尺度结构减少,并且他们发现高雷诺数时,近壁区出现较强的流向涡结构。 Ouro等人[38]通过实验和LES数值模拟研究了近壁面圆柱绕流的近尾迹动力学行为,主要考虑的间隙比为0.5和1.0,雷诺数为6 666、10 000和13 333。需要注意的是,在Ouro等人的实验和数值模拟中,圆柱均位于壁面边界层内,且壁法线方向高度为3D,上边界条件为自由面,因此除了壁面边界层还有自由面对圆柱尾流产生影响,而Ouro等人更多关注的是下壁面对圆柱绕流近尾迹的动力学行为。实验和数值模拟结果均反应了近壁效应导致的圆柱绕流近尾迹的抬升效应。G/D=0.5时,下壁面显著影响了涡的产生和脱落,导致尾迹的非对称分布随着Re增加而更加明显;G/D=1.0时,尾迹相对对称。数值模拟流场的展向涡量(图7)展示了近尾迹的流动结构。不同于前文提到的低雷诺数流动现象,相对较高的雷诺数导致圆柱上下侧的剪切层发生了Kelvin-Helmholtz(KH)不稳定。在KH不稳定之后,剪切层分解成小涡(KH涡),并在向下游演化的过程中与完全湍流状态的近尾迹合并。KH不稳定在圆柱上下侧发展,过程是解耦的,即其产生过程并非是同步的。图8展示了瞬时流场的涡结构等值面,其中虚线标记的结构即为KH涡,KH涡从圆柱上下侧的转捩剪切层分离之后,展向分布并不平行于圆柱,而是呈波浪形,且展向波数约为πD/2,与Braza等人[39]的研究结果一致。尾流向下游演化的过程中出现了涡分裂和涡不连续现象。 图7 LES数值模拟瞬时流场涡量云图[38]:(a) G/D=0.5,Re=6 666;(b) G/D=1.0,Re=13 333。颜色代表涡量旋转方向 图8 LES数值模拟瞬时流场Q准则识别的涡结构等值面[38],G/D=0.5,Re=13 333。色带代表壁法线高度。虚线标注的是KH涡;箭头标记的是涡分裂和涡不连续 上文提到近壁圆柱绕流尾涡会诱导下壁面边界层失稳,形成二次涡结构(图4),并在壁面附近产生与圆柱上表面脱落涡相同旋转方向的二次涡结构。图5同时展示了二次涡的运动轨迹。这些二次涡的演化会对壁面边界层的发展产生重要作用。 Kyriakides等人[40]首次实验研究了近壁圆柱绕流尾流诱导的转捩边界层。他们发现壁面边界层转捩区存在二次涡,并利用象限分析对二次涡的产生过程做出了解释,预测了边界层转捩受二次涡的影响。Ovchinnikov等人[41]利用DNS和LES数值模拟了近壁圆柱绕流,并考虑了雷诺数影响。他们在壁面边界层转捩区并未发现二次涡结构,但是观察到了沿展向分布的高低速条带结构。他们认为这些条带结构与高湍流度自由来流(free stream turbulence, FST)影响下旁路转捩的Klebanoff模式[42-43]类似,并发现这些结构源于近壁区的流向涡,其在向下游演化过程中高低速条带二次失稳对湍流边界层的发展起关键作用。 Pan等人[16]结合流场可视化和速度测量显示了近壁圆柱绕流尾流诱导边界层转捩。他们在实验过程中观察到了壁面边界层对圆柱尾流卡门涡街的响应,即生成了展向分布的二次涡结构,这与Kyriakides等人[40]的实验结果一致。Pan等人展示了二次涡结构二次失稳并最终形成发卡涡的过程,如图9所示。圆柱尾涡诱导了主发卡涡(由二次涡失稳演化而来)的生长,主发卡涡通过涡与壁面的相互作用,诱导了高阶发卡涡的生成,高阶发卡涡再次诱导新的发卡涡,这样就生成了发卡涡包和相关的条带结构。在转捩过程中,发卡涡、发卡涡包和条带结构的动力学行为和自维持机制与湍流边界层一致,最终形成了自维持的湍流边界层。因此,他们认为近壁圆柱绕流尾流诱导边界层转捩的路径不同于Klebanoff模式。Mandal和Dey[44]的实验也得到了相似的结论。 图9 近壁圆柱绕流诱导边界层转捩过程中,二次涡向发卡涡发展的过程[16]。二次涡由字母A标记,演化为发卡涡A和B He等人[45]的实验结果也证实了二次涡结构的存在,并计算了圆柱尾流诱导边界层失稳过程中边界层内扰动能量沿流向方向的变化,其表现为两个阶段的增长:第一阶段呈指数型增长,第二阶段增加较慢。两个增长阶段与近壁区二次涡形成和失稳相关。他们利用动态模态分解技术得到了时域正交模态,结果显示第一阶段扰动能量的增长与圆柱尾涡脱落密切相关,而第二阶段是多频扰动增长,特别是低频扰动的增长。He等人[46]考虑间隙比相对较小(G/D=1.0)时,圆柱尾流与边界层的相互作用。他们在实验中也观察到了二次涡,但是由于圆柱尾流与边界层的相互作用较强,二次涡的演化呈现不一样的过程:二次涡要么被夹带进圆柱尾涡,要么被推向壁面。这就导致了一个快速的三维扰动过程,通过这个扰动,流向涡被生成,而这些流向涡是之后导致边界层转捩的主要结构。 He等人[47]以拉格朗日的角度实验研究了由圆柱尾流引起的壁面边界层转捩中的拉格朗日拟序结构(Lagrangian coherent structures, LCS)。LCS由有限时间Lyapunov指数(FTLE)揭示[48-51]。近尾迹LCS如图10(a)所示,圆柱后方的大尺度卡门涡街拟序结构在壁面诱导了二次涡的生成,随后二次涡快速发展,逐渐抬升偏离壁面。转捩区和充分发展的边界层中发卡涡结构分别如图10(b)和10(c)所示。He等人还从PIV数据中提取出LCS的平均对流速度和平均倾角。LCS结构倾角逐渐增加直至转捩中期达到峰值,这是因为二次涡失稳,流向方向被拉长,其涡头会抬升,导致倾角增加。这种抬升过程会持续到转捩边界层,形成主发卡涡。此时发卡涡已经远离壁面。然而,在向下游演化过程中,大尺度发卡涡包的形成导致了非常长的流向结构。这些非常长的结构的流向倾角通常比单个发卡涡小,导致充分发展的湍流边界层内LCS倾角小于转捩边界层内的LCS倾角。 图10 近壁圆柱绕流尾流引起边界层转捩中的拉格朗日拟序结构演化[47]。(a)近尾迹的拉格朗日拟序结构时空演化。矢量箭头为脉动速度;字母标记的结构为二次涡。(b)转捩边界层中的发卡涡结构时空演化。字母标记的是发卡涡的涡头。(c) 充分发展的湍流边界层中发卡涡包的时空演化。字母标记的是组成发卡涡包的发卡涡涡头;直线是发卡涡涡头的连线 近壁圆柱绕流中尾流与边界层相互作用的过程是复杂的多尺度动力学过程,在不同尺度的湍流结构相互作用过程中,会产生丰富的湍流结构。研究者对此问题已经开展了大量的研究,发现间隙比、边界层厚度和雷诺数对圆柱升阻系数以及涡脱落频率产生不同程度的影响。圆柱上下尾涡和二次涡的演化受间隙比影响较大:小间隙比时,圆柱下尾涡诱导边界层分离形成二次涡,二次涡快速抬升与圆柱上尾涡合并,此过程导致圆柱下尾涡被拉伸破坏形成小尺度结构;大间隙比时,正常脱落的圆柱尾涡与壁面边界层相互作用,致使边界层分离形成二次涡结构,涡轨迹追踪显示二次涡向下游演化的过程中未与圆柱尾涡合并。对于圆柱尾流诱导壁面边界层转捩的原因,研究者们保持不同的观点:观点一,圆柱尾涡诱导边界层内产生条带结构,条带结构的二次失稳导致边界层转捩;观点二,二次涡受圆柱尾涡诱导而出现三维失稳,演变成主发卡涡,主发卡涡诱导新的发卡涡,形成发卡涡包,此过程边界层发生转捩。 以上综述表明,尽管研究者们对近壁面圆柱绕流问题进行了丰富而深入的研究,但是仍然存在不足,后续需要进一步研究的内容包括以下方面: (1)现有的实验测量均是对流场中心面进行二维PIV拍摄,对相互作用过程中复杂流场的三维实验测量研究较少。然而不同尺度湍流结构产生、发展、维持和衰减是湍流研究的重点之一,为了刻画湍流结构的演化需要进行精细的三维实验测量,获取三维实验数据。当然也可以通过数值模拟获取三维流场数据,但是全尺度解析的直接数值模拟方法需要大量的计算资源,而使用LES方法可能无法获取部分重要的小尺度结构,这对近壁圆柱绕流问题的深入研究带来很多困难。 (2)目前近壁圆柱绕流流动结构的研究对小间隙比情况关注较少。较小的间隙比会导致圆柱尾流与壁面边界层的相互作用更加复杂,刻画结构演化规律需要进一步的实验测量和数值模拟。 (3)雷诺数也是此问题重要的参数,目前对高雷诺数下近壁圆柱绕流流动结构时空演化的研究较少,因此高雷诺数对不同尺度的湍流结构产生、发展、维持和衰减产生的影响有待进一步研究。 (4)以往研究对近壁圆柱尾流诱导壁面边界层转捩(即圆柱上游为层流边界层)的关注较多,但是湍流边界层(即圆柱上游为湍流边界层)受圆柱尾流影响的研究较少,因此湍流边界层内复杂的壁湍流结构与圆柱尾流的相互作用也是今后值得深入研究的重要课题,尤其需要关注相互作用过程中不同尺度间动量和能量的输运。 关注近壁圆柱绕流尾流与壁面边界层相互作用的动力学行为,对湍流结构的演化过程进行精细刻画,定量描述相互作用过程中湍流结构动量和能量在不同尺度上的输运规律,最终揭示其物理机理,从而丰富湍流理论基础并为工程应用的尝试提供支撑。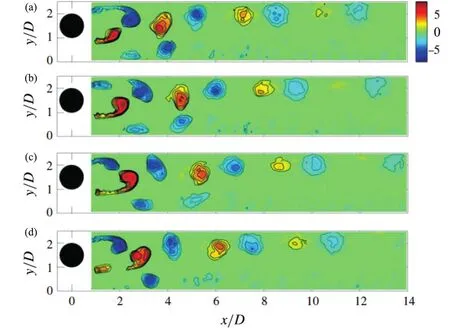



2 圆柱尾流对边界层发展的影响

3 总结与展望

