冲击载荷下结构陶瓷的失效与破碎特性研究

党泉勇，徐 鹏

(1.山西大同大学 建测学院，山西 大同 037003；2.中北大学 理学院，山西 太原 030051)

AD95陶瓷具有强度高、密度低、硬度大等优异的力学性能，在冲击防护领域有着广泛的应用.然而，受陶瓷烧结工艺限制，AD95陶瓷材料微观结构往往存在微裂纹、微孔洞和晶界缺陷等，诸多影响因素导致材料在冲击加载下常表现为脆性特征.因此，研究该结构陶瓷在不同应变率下的失效强度、动态破碎与损伤机理以及破碎后碎片分布尺度规律等，对理解陶瓷材料在冲击加载下的破坏过程至关重要.数值模拟可以在一定程度上完成对实际工况的构建和重现，也可为解释各种冲击压缩与撞击破碎的复杂现象提供新见解.碎裂过程必然伴随着载荷快速释放带来的应力波传播，以及多个裂纹的同时激发和作用，这种“动态压缩/撞击破坏”带来的材料“动态破碎”过程，有待于开展深入研究[1-6].

陶瓷等脆性材料的力学性能对加载应变率通常较为敏感，针对这种特性，研究人员以应变率量级为依据，将材料性能的测试方法对应应变率从低到高依次进行归类总结，如图 1 所示.其中，在冲击动力学领域的两个最典型测试方法为Hopkinson杆和平板撞击实验[7-9]，可分别测试材料在中高应变率和极高应变率下的力学性能.

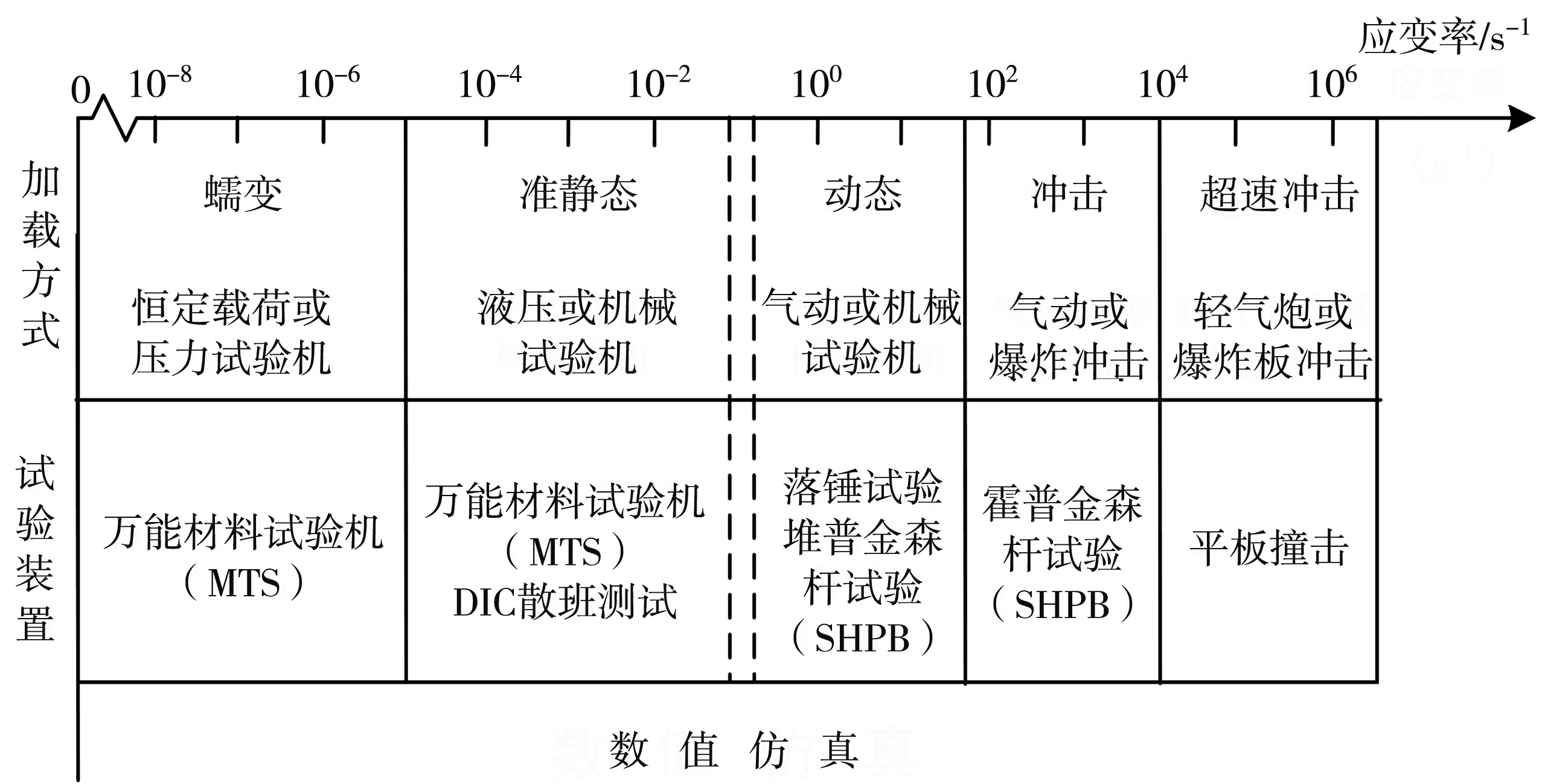
图 1 不同应变率下力学性能测试方法[10]

本文在实验的基础上，通过AUTODYN软件，分别模拟了平板撞击与霍普金森杆压缩实验，采用应用较为广泛的陶瓷本构模型即Johnson-Holmquist II(JH2)模型[11-13]，对陶瓷在一维应力与一维应变下的损伤与破碎特性进行了数值仿真，再现了实际工况下的试样失效历程.

1 实验与仿真设置

1.1 实验设置

本文陶瓷材料选用热压烧结成型的AD95陶瓷，密度为3 869 kg/m3.动态霍普金森压缩实验试样为直径5.5 mm，长11 mm的圆柱，弹性模量为290 GPa，准静态下的材料强度为2.8 GPa.压杆直径为14.5 mm，入射和透射杆长度为 1 300 mm.撞击杆长度选用250 mm，完成了对试样300 s-1～800 s-1应变率之间的加载.为防止试样对压杆端部的破坏，两者之间添加WC垫块，根据波阻抗匹配原则，垫块尺寸Φ10.3mm×5mm.为增加入射波加载时间，减小波在压杆内的弥散，使用塑性变形能力较好的紫铜作为波形整形器，尺寸为Φ6×2 mm[14].平板撞击实验采用对称碰撞形式，飞片和3层试样均采用AD95陶瓷，尺寸均为Φ20 mm×2 mm.飞片速度分别为68 m/s～200 m/s，获得的冲击应力分别为4.2 GPa～9.1 GPa.3层试样之间放置PVDF压电传感器测量冲击波压力，并使用环氧树脂胶对试样进行24 h固化封装处理.

图 2 实验试样

1.2 有限元模型

一维应力加载下，有限元几何模型与实验设置相同，模型各部分均采用Lagrange网格进行描述，如图 3 所示.观察回收的破碎试样颗粒尺寸发现，试样网格大小应小于100 μm才能准确描述脆性陶瓷材料动态加载下的损伤和破碎效果.此外，在压杆与试样、整形器、垫块等接触端部，将网格做局部细化处理，几何模型详细网格尺寸见表 1.

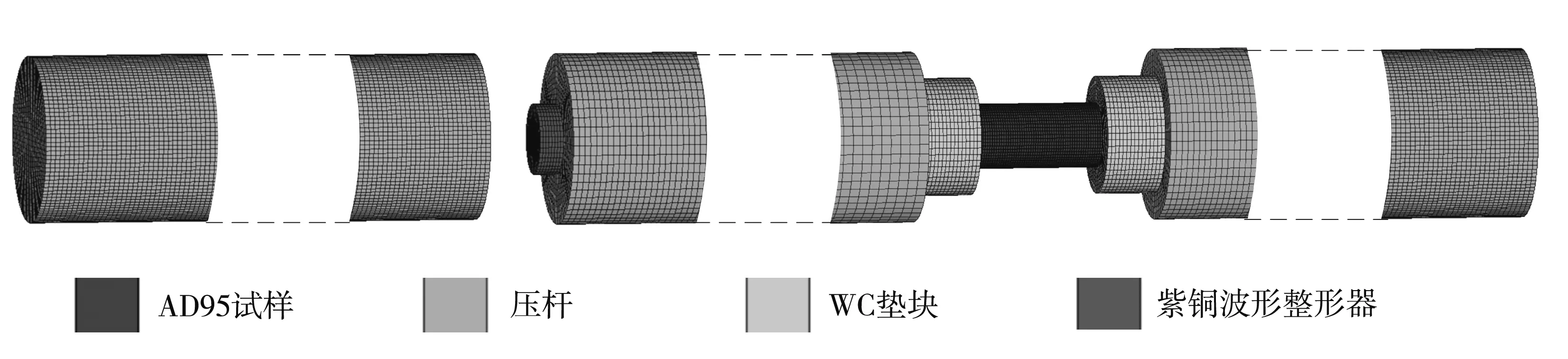
图 3 Hopkinson有限元模型

表 1 单元网格尺寸

一维应变加载下，仿真模型与实验设置一致，飞片和试样均采用SPH无网格方法建模，以避免高速撞击中两者网格畸变导致的计算中断和误差过大等问题.其中，SPH粒子影响域半径为100 μm，具体几何模型如图 4 所示.

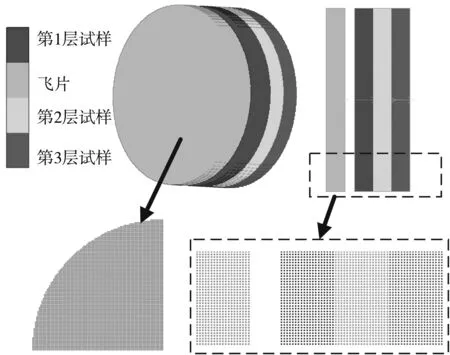
图 4 平板撞击模型

1.3 材料模型

冲击加载下陶瓷材料的损伤、破碎过程异常复杂，且随着加载速率的增加材料会表现出一定的应变率效应、非弹性变形等机制，故选取合适的材料模型是冲击加载下陶瓷材料数值仿真计算的关键因素.

JH2本构模型发展了Drucker含损伤的屈服面演化理论，建立了陶瓷强度随损伤累积而连续减小的对应关系.当损伤因子D>0时，损伤开始累积，对应强度将随着塑性应变的增加而逐渐出现劣化现象，如图5所示.

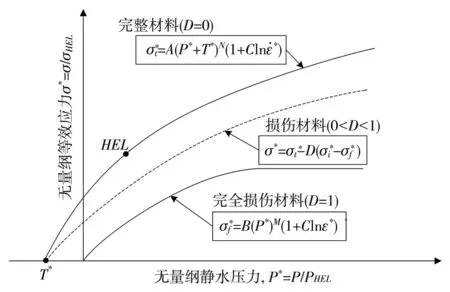
图 5 含损伤的JH2本构模型

由图5可知，JH-2模型中材料的无量纲等效应力可表示为

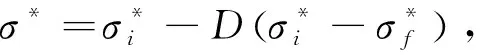
(1)

式中：D为材料损伤因子；材料在未损伤(D=0)和完全损伤(D=1)情况下，无量纲等效应力分别为

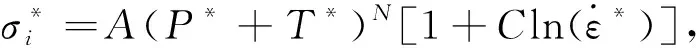
(2)

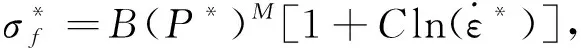
(3)

高温高压情况下，材料的状态方程可采用多项式的形式

P=K1μ+K2μ2+K3μ3+ΔP,

(4)

式中：K1(体积模量),K2,K3为材料常数；μ为压缩体应变，μ=ρ/ρ0- 1.

AD95陶瓷的JH2本构模型参数如表 2 所示.根据实验获得各部分变形情况，压杆采用线弹性模型，紫铜波形整形器和WC垫块均采用Johnson-Cook(JC)本构模型和Shock 状态方程描述，具体材料参数如表 3 所示.

表 2 AD95陶瓷本构参数[15]

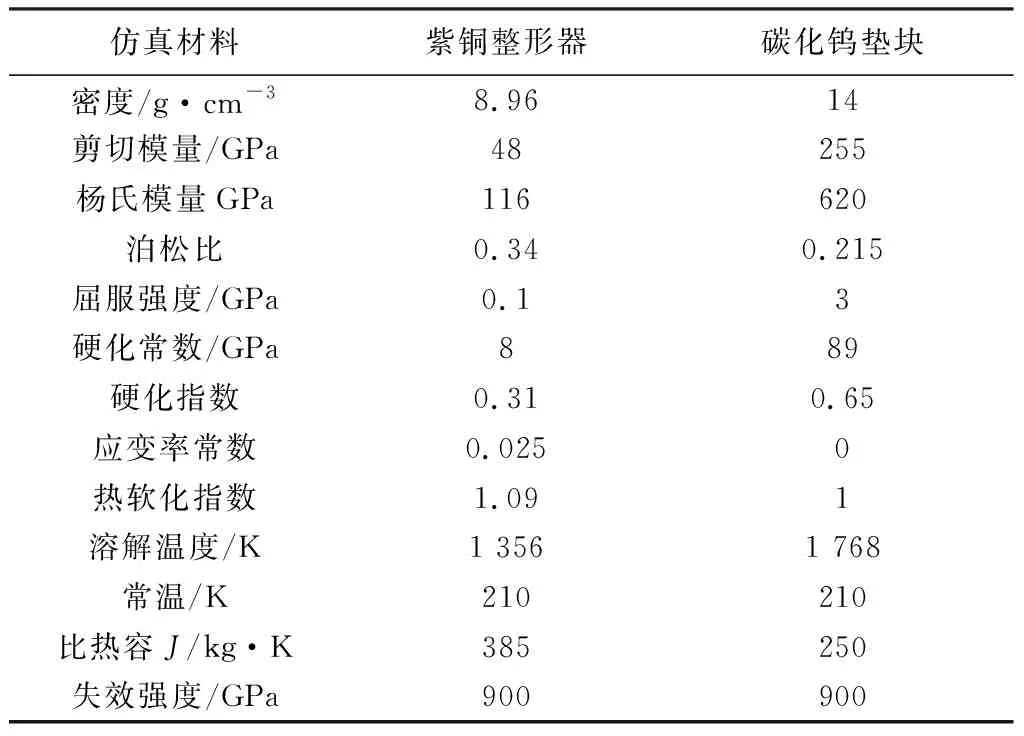
表 3 紫铜及碳化钨的材料参数

2 结果与分析

在一维应力加载下，AD95陶瓷的数值仿真中，对入射杆和透射杆中间位置单元提取应变历程曲线，与试验结果对比，如图 6 所示.由图 6 可知，仿真和试验结果吻合度较好，可认为数值模拟结果是有效的.同时，反射波历程存在一个平台段，持续时间约为180 μs左右，表明入射波波形实现了对试样的恒应变率加载.在恒应变率加载后，反射波信号瞬间增大，透射波信号消失，说明在应力加载一定时间后，试样波阻抗瞬间减小，材料在瞬间被压垮.

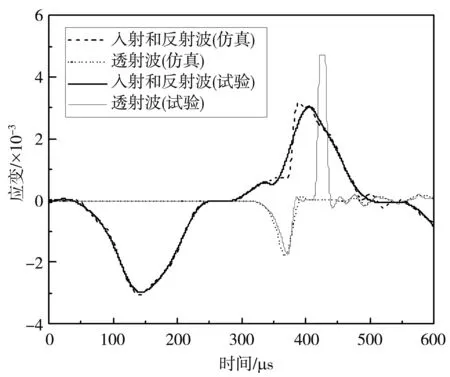
图 6 试验和仿真对比图

设试样开始发生损伤时间为t时刻，仿真提取试样的损伤云图历程以及试验回收的破碎后陶瓷颗粒如图 7 所示.

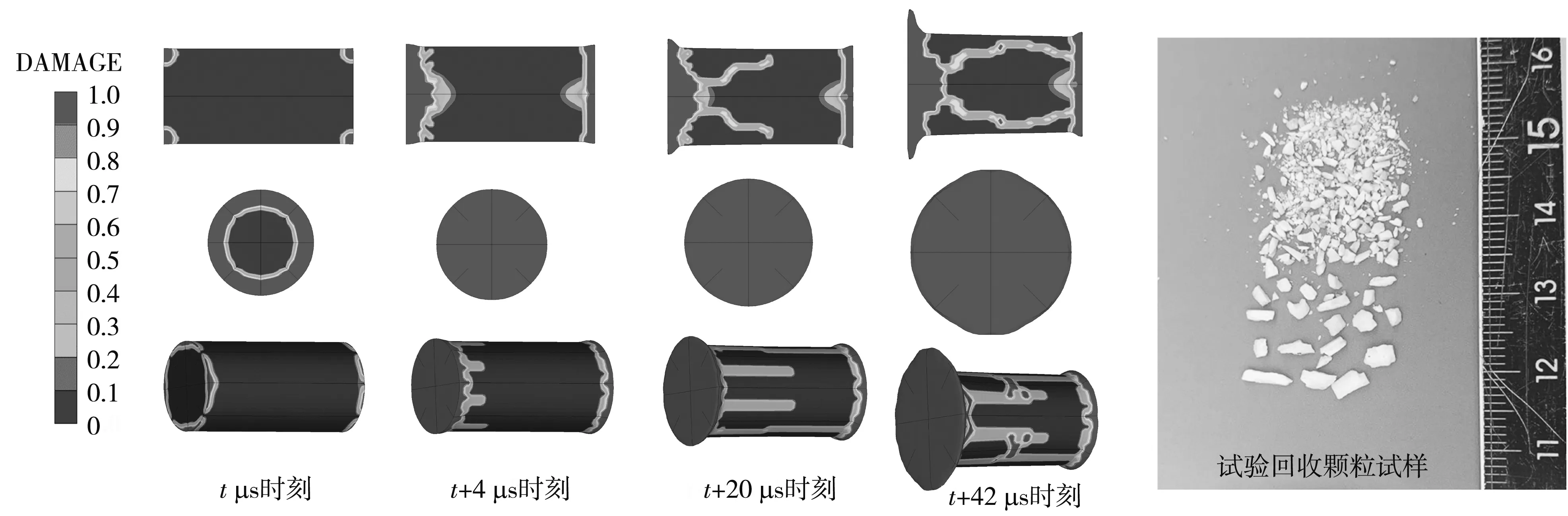
图 7 一维应力波加载下试样的损伤

由图 7 可知，受应力集中影响，圆柱试样底面棱角处最先发生损伤，在t+4μs时刻，试样的端面已完全损伤.随着应力波的持续加载，试样端面的不规则变形使得裂纹由圆柱试样内部和外部同时产生沿纵向方向的裂纹.至t+42 μs时刻，纵向裂纹完成了贯穿，并出现了多条横向裂纹，至此试样失去了对压缩波的承载能力，直至材料完全破碎.试验中，观察回收试样也发现，大颗粒陶瓷主要发生在圆柱试样的外圆周面，而小颗粒陶瓷多来自于端面损伤较严重位置.因此，在冲击压缩下，尽管AD95陶瓷整体被压垮在一瞬间，但材料损伤以及裂纹扩展需要一定的时间完成.

为获得陶瓷试样具体的受力和损伤状态，对1/4圆柱试样设置高斯点，即在试样端面以及中间部位沿着径向布置5个高斯点，在轴向同样均匀布置5个高斯点，如图 8 所示.

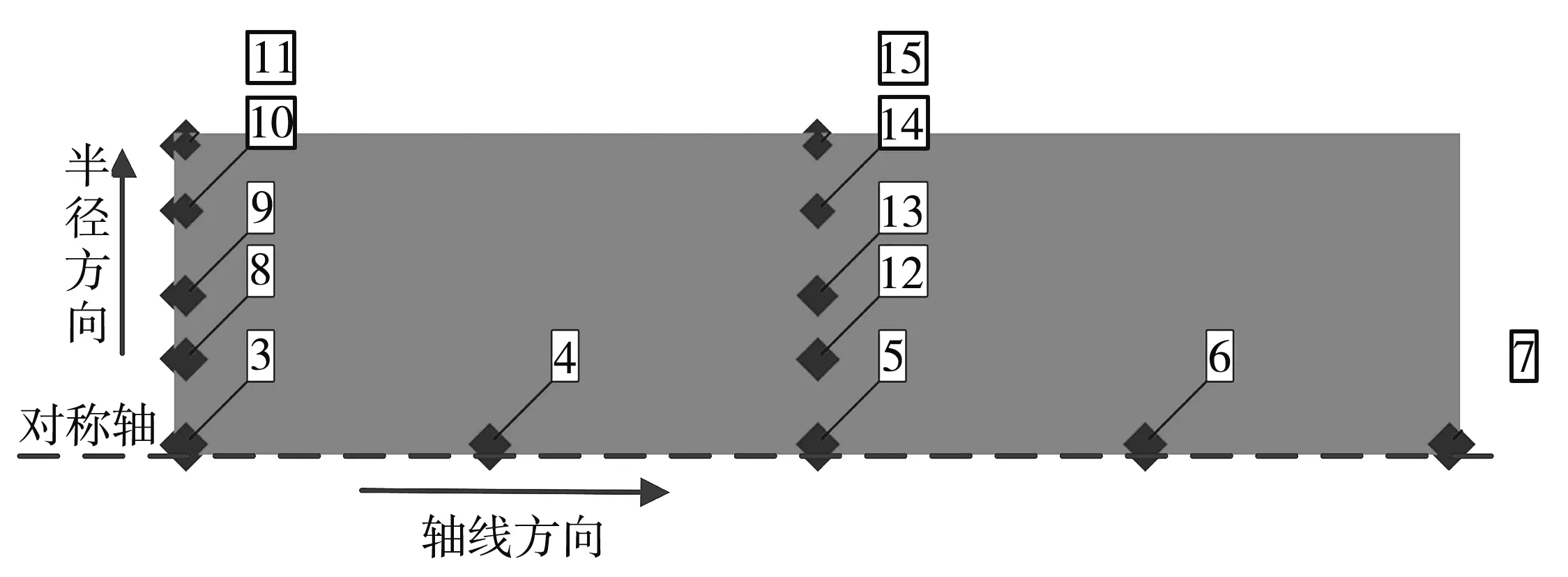
图 8 高斯点分布图

图 9 表明，在一维应力波加载下，圆柱试样中部应力增加较缓慢，两底面处(#3和#7号点)应力有突变，应力在瞬间增加，存在明显的应力集中.在圆柱底面沿直径方向，试样的应力集中程度也不同，应力最大值出现靠近中心位置处，即#8号和#3号点.

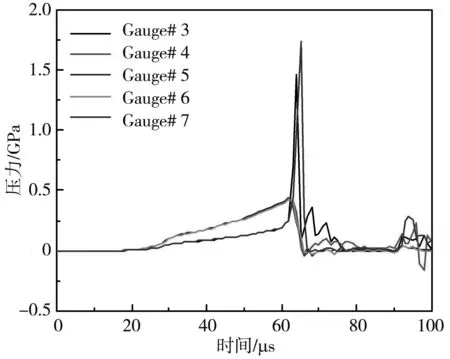
(a) 圆柱底面应力轴向分布

图9(c)表明，圆柱中间位置应力相差较小，说明此处为应力均匀状态，且相比圆柱两底面处，应力减小许多.因此，圆柱形试样在一维应力波作用下，材料的破坏主要源自圆柱两端面，试样的破碎主要归功于端面应力集中，以及后续纵向裂纹的扩展和汇集.

本文平板撞击试验测得的冲击波压力小于材料的Hugoniot弹性极限.图 10 为平面冲击波作用下试样的仿真损伤历程和试验回收的破碎后陶瓷颗粒.由仿真结果可知，当飞片撞击试样瞬间，飞片与试样界面各自产生了破坏面，并向材料内部传播.当应力波到达试样自由端面后，形成的破坏面将反向传播进入试样.在试样内，由于边侧稀疏波的作用，有一条裂纹沿圆片试样侧面约呈40°的方向，并迅速扩展.同时，试样中间区域在t+1.0 μs时刻，出现了明显的层裂现象，这是由于撞击产生的压缩波在加载方向两自由面各自反射稀疏波在此相遇引起.本文AD95陶瓷实测的抗拉强度为0.33 GPa，远小于冲击应力3 GPa，故此处材料失效是由于抗拉强度不足造成的.

最后，试样表面的裂纹密度并非均匀，中间和外围区域的裂纹密度较小，而中间压缩应力波直接作用区域的裂纹密度最大.由试验回收的陶瓷颗粒可知，试样的破坏存在明显的分层，且大颗粒的陶瓷主要来源于面板周围，以及圆片外侧即受边侧稀疏波影响区域.

图 10 平面冲击波加载下试样的损伤

3 结论

本文通过模拟AD95陶瓷的SHPB试验与平板撞击试验，再现了实际工况下材料内部的损伤历程，并与实验结果进行了对比，验证了数值模型的有效性.主要结论如下：

1) 在实现恒应变率加载后，某一时刻试样波阻抗瞬间减小，材料在一瞬间被压垮.提取材料内部损伤历程发现，在陶瓷整体被瞬间压垮前，试样仍具有承载能力.圆柱形试样在一维应力波作用下，材料破坏始于两端面，后续纵向裂纹的扩展和汇集造成了材料的完全破碎.

2) 平面冲击波作用下，试样在低于Hugoniot弹性极限下存在两个相向传播的破坏面.由于边侧稀疏波的作用，裂纹在与圆片试样侧面约呈40°的方向迅速扩展.同时，由于应力波的相互作用以及材料本身抗拉强度不足，造成试样内出现了明显的层裂现象.