即墨铁路物流中心运量预测研究

何西健，屈拴科，赵春展

(中铁二院工程集团有限责任公司 北方公司，山东 济南 250012)

即墨铁路物流中心建成于2019年，是全路一级铁路物流中心[1-3]，其建成后根据客户运输距离及货运品类的不同，通过公路、铁路不同运输方式运输，合理分工降低物流成本，逐步实现“公转铁”目标。研究灰色关联度多元回归模型预测即墨铁路物流中心运量，合理确定物流中心功能区规模，为即墨铁路物流中心的功能布局提供指导。

1 即墨铁路物流中心现状

1.1 区域概况

即墨铁路物流中心位于山东半岛东部的青岛市即墨区，该区域近年来着力构建现代产业体系，积极培育新能源等新兴产业，加快造船、汽车等先进制造业发展，提升传统产业，聚集发展物流、商贸等现代服务业。产业发展所需原材料来源于全国各地，产成品销往全国各地及海外市场，“两头在外”的特征十分显著，区域内蕴含的物流运输需求巨大。

1.2 功能定位及运输现状

根据地方规划，即墨铁路物流中心周边分布有黄岛、娄山、胶州、董家口4个铁路物流中心。相邻各物流中心功能定位如下：黄岛铁路物流中心是以小汽车、油品发送为主的专业物流中心，主要服务于黄岛区；娄山铁路物流中心是以澳柯玛、海尔、海信等家电为服务对象的物流中心，主要服务于老城区；胶州铁路物流中心依托青岛集装箱中心站，是以集装箱运输、多式联运为主要业务的物流中心，主要服务于胶州市；董家口物流中心主要服务董家口临港产业园区。从地理位置分析，即墨铁路物流中心与其它4座物流中心的重点服务范围划分清晰，结合项目周边产业布局情况和周边铁路物流中心的核心业务，即墨铁路物流中心定位以城市配送、小汽车发送、汽车配件专业市场等为主要业务的综合性物流中心，主要服务于城阳区、市北部，通过公路、铁路辐射至烟台、威海、潍坊、日照等区域，辐射济南及以远的全国各地。

结合即墨铁路物流中心定位和服务范围，对周边重点企业开展运输需求调查。从调查结果看，运输需求重点集中在商品小汽车、钢铁、建材、木材、机械等品类，重点服务企业2009—2020年运量如表1所示。

表1 重点服务企业2009—2020年运量表 万tTab.1 Current traffic volume of key service enterprises from 2009 to 2020

2 运量预测模型构建

传统的铁路货场运量预测多采用增长率法、弹性系数法进行分析，预测模型采用单一影响因子分析，预测精度受单一影响因子数据波动影响较大。灰色关联度多元回归模型根据灰色关联分析理论[4]选取多个关键影响因子，进而建立多元回归模型，减少单一影响因子数据波动对预测数据的影响；选定的影响因子采用Gomperz成长曲线模型进行延伸性预测，预测值代入建立的灰色关联度多元回归模型预测即墨铁路物流中心运量。

2.1 灰色关联度影响因子

铁路物流中心通过发挥物流功能的主导作用，可以产生较强的带动效应。在带动和促进本地区产业集聚和发展的同时，有效地延长产业链，对周边腹地经济产生明显的辐射功能。铁路物流中心的服务范围将周边30 ~ 50 km核心圈层范围内的重点企业定位为核心服务对象，通过省内公路、铁路辐射省域的中圈层，依托既有铁路路网及高速公路网络，辐射全国的外圈层。铁路物流中心运量影响因子分别选取3个圈层的全社会物流量、国内生产总值、第二产业增加值、第三产业增加值共12个影响因子作为分析对象，分析与物流中心运量的关联度。

2.2 灰色关联度

灰色关联度分析是根据各因素变化曲线几何形状的相似程度，来判断因素之间关联程度的方法；此方法通过对动态过程发展态势的量化分析，完成对系统内时间序列有关统计数据几何关系的比较，求出参考数列与各比较数列之间的灰色关联度[6]。灰色关联度计算分析步骤如下。

（1）为消除影响因子不同量纲的影响，首先对数据进行无量纲化处理，得出序列值。

式中：Xkt’为第k项影响因子第t年序列值，k为影响因子变量，初始值取0，k= 0，1，2，…，12；k取0时，X0t为物流中心第t年运量，t为时间变量，初始年t取0，t= 0，1，2，…，9；Xkt为第k项影响因子第t年原始数据，k= 0，1，2，…，12，t= 0，1，2，…，9；Xk0为第k项影响因子第0年原始数据。

（2）将得出的序列值进行求差处理，求差公式为

式中：Δkt为第k项影响因子第t年的序列值与物流中心运量第t年的序列值差的绝对值；X0t’为物流中心运量第t年的序列值。

（3）求关联因子最大差maxΔkt与最小差minΔkt。

（4）计算灰色关联度。

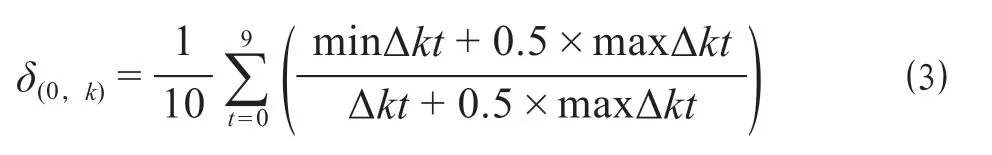
式中：δ(0，k)为第k项影响因子序列值与物流中心运量序列值的关联度。

2.3 基于灰色关联度多元回归模型构建

基于灰色关联度多元回归模型是一元线性回归模型的扩展，能够有效消除一元线性回归模型中单一自变量对因变量的影响程度。根据灰色关联度分析结果，选取关联度高的3个因素为灰色关联关键因子，建立基于灰色关联度多元回归模型如下。

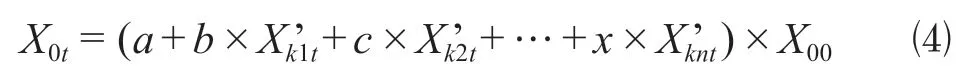
式中：Xk1t’ 为k个影响因子中选定的第1个关键因子序列值；Xk2t’ 为k个影响因子中选定的第2个关键因子序列值；Xknt’ 为k个影响因子中选定的第n个关键因子序列值，其中n= 3，4，…，12；X00为初始年物流中心运量；a，b，c，…，x为统计分析结果参数值。

2.4 建立运量预测模型

通过拟合历史统计数据，建立能描述其发展过程的Gomperz成长曲线[8]，以模型外推对关键因子2030年增长率进行预测。预测基本模型为

式中：αt为时间t的单关键因子预测值；ρ，f，g为参数。

3 即墨铁路物流中心运量预测实证分析

3.1 灰色关联度影响因子

以即墨铁路物流中心辐射范围内签订框架协议的重点企业2009—2020年统计数据为基础数据，运量影响因子选取3个圈层的12个影响因子作为分析对象，指标如下。X1t为第t年青岛市全社会物流量，万t；X2t为第t年青岛市GDP，亿元；X3t为第t年青岛市第二产业增加值，亿元；X4t为第t年青岛市第三产业增加值，亿元；X5t为第t年山东省GDP，亿元；X6t为第t年山东省全社会物流量，万t；X7t为第t年山东省第二产业增加值，亿元；X8t为第t年山东省第三产业增加值，亿元；X9t为第t年全国GDP，亿元；X10t为第t年全国全社会物流量，万t；X11t为第t年全国第二产业增加值，亿元；X12t为第t年全国第三产业增加值，亿元。影响因子选取2009—2020年国家及地方统计数据为基础数据进行分析。

3.2 灰色关联度计算

对即墨铁路物流中心选定的12个影响因子2009—2020年原始数据进行统计，为数据无量纲化处理提供基础数据。根据公式(1)，对数据进行无量纲化处理。数据无量纲化序列值如表2所示。

表2通过对各影响因子数据无量纲化处理，消除影响因子不同量纲的影响。根据公式(2)，对无量纲化序列值进行求差处理。无量纲化序列差如表3 所示。

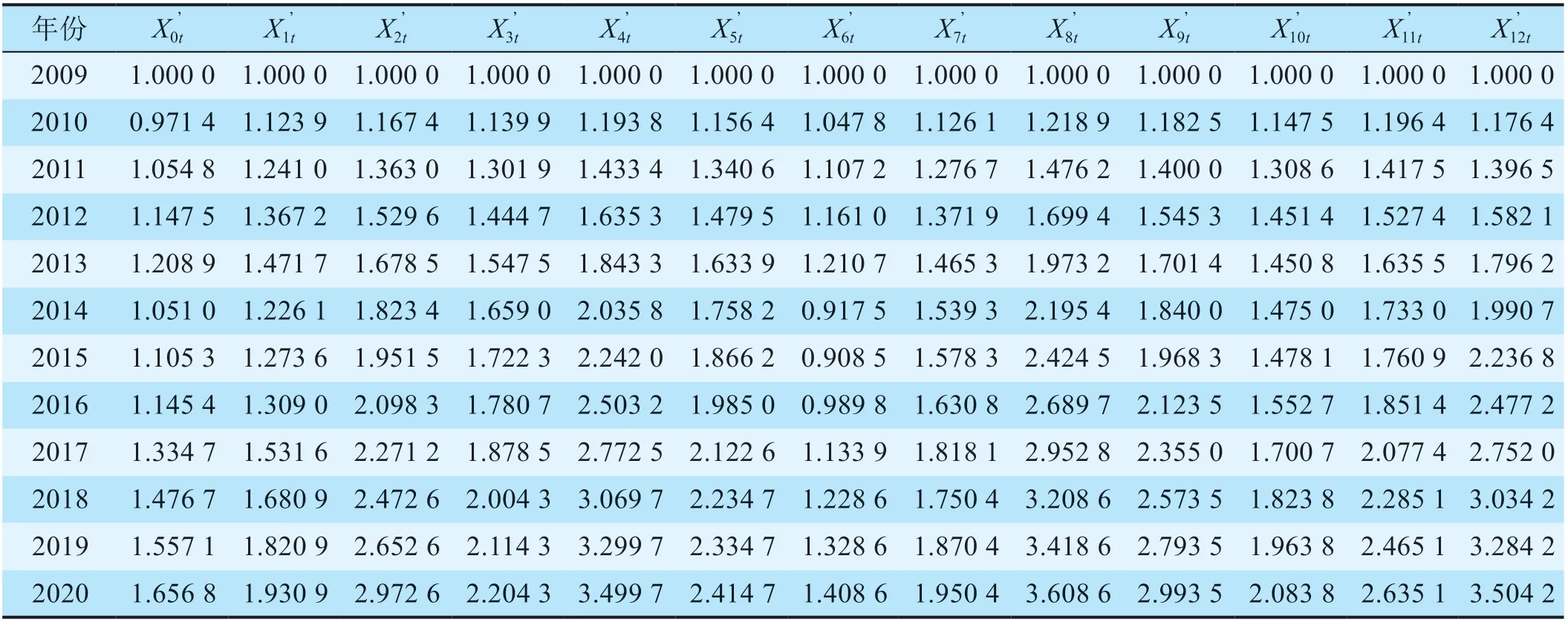
表2 数据无量纲化序列值Tab.2 Dimensionless sequence value of data

表3通过第k项影响因子第t年的序列值与物流中心运量第t年的序列值差的绝对值，得出关联因子最大差与最小差，为根据公式(3)计算灰色关联度提供数据支撑。根据公式(4)，计算各影响因子序列值与物流中心运量序列值的关联度。灰色关联度如表4所示。

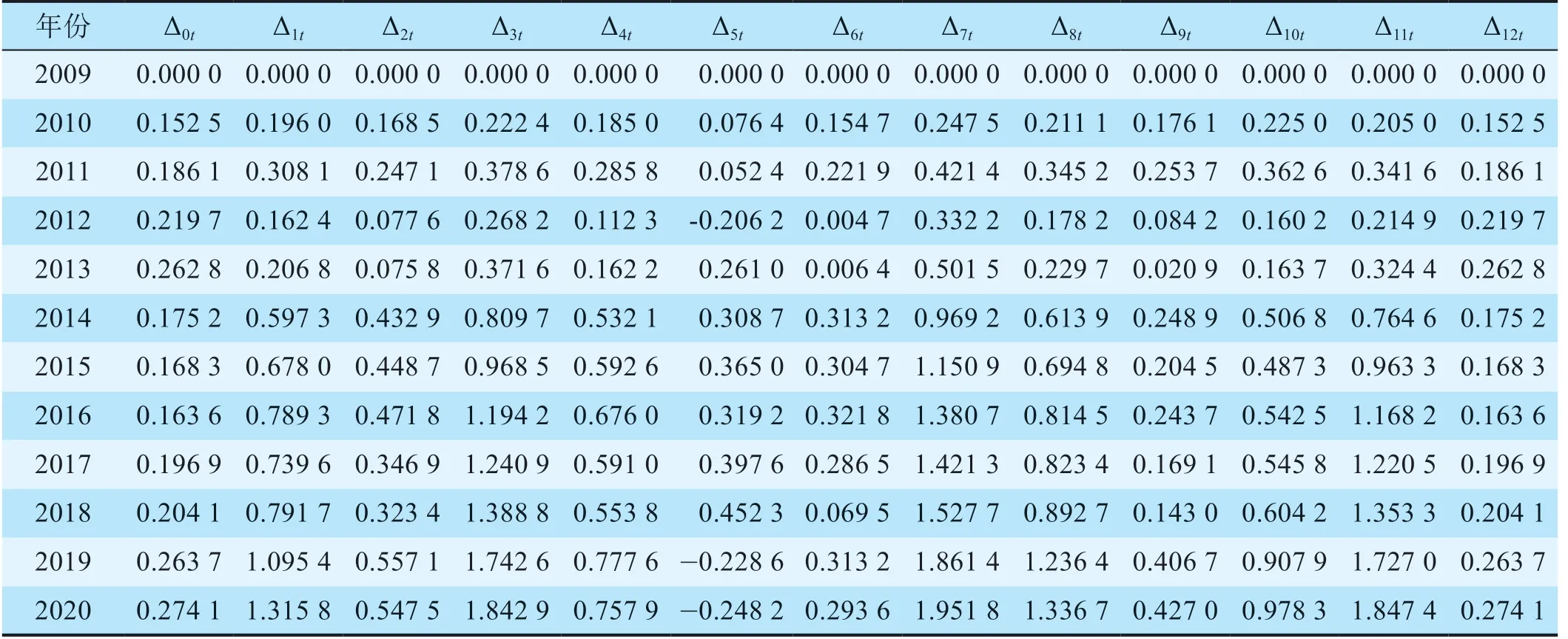
表3 无量纲化序列差Tab.3 Dimensionless sequence difference

表4 灰色关联度Tab.4 Grey correlation degree

根据灰色关联度分析结果可以看出，青岛市全社会物流量X1t、山东省全社会物流量X6t、全国国民生产总值X9t3个因素对即墨物流中心物流量的影响程度高于其他因素，因此选定该3项影响因子为关键因子。

3.3 基于灰色关联度多元回归模型建立

根据灰色关联度分析结果，选取关联度高的3个因素为灰色关联关键因子。结合表3中该3项关键因子数据无量纲化序列值，建立基于灰色关联度多元回归模型如下。

通过回归模型分析复测定系数R2是否接近1，F显著性统计量(Significance F)是否小于0.05，判定回归效果是否显著；建立的即墨铁路物流中心灰色关联多元回归模型中，复测定系数R2= 0.992 8，接近1，模型的拟合优度高；F显著性统计量= 8.87×10-6< 0.05，回归方程显著有效。

3.4 基于灰色关联度多元回归模型精度检验

利用建立的基于灰色关联度多元回归模型和传统弹性系数法[8]分别对即墨铁路物流中心物流量进行预测，并与实际值进行相对误差分析。基于灰色关联度多元回归模型预测值与弹性系数法预测值误差分析如表5所示。

根据表5分析结果可知，基于灰色关联度多元回归模型能够有效降低单一因素影响程度；从相对误差分析来看，基于灰色关联度多元回归模型较传统的弹性系数法预测相对误差更小，且相对误差基本呈正态分布，可信度明显提高。

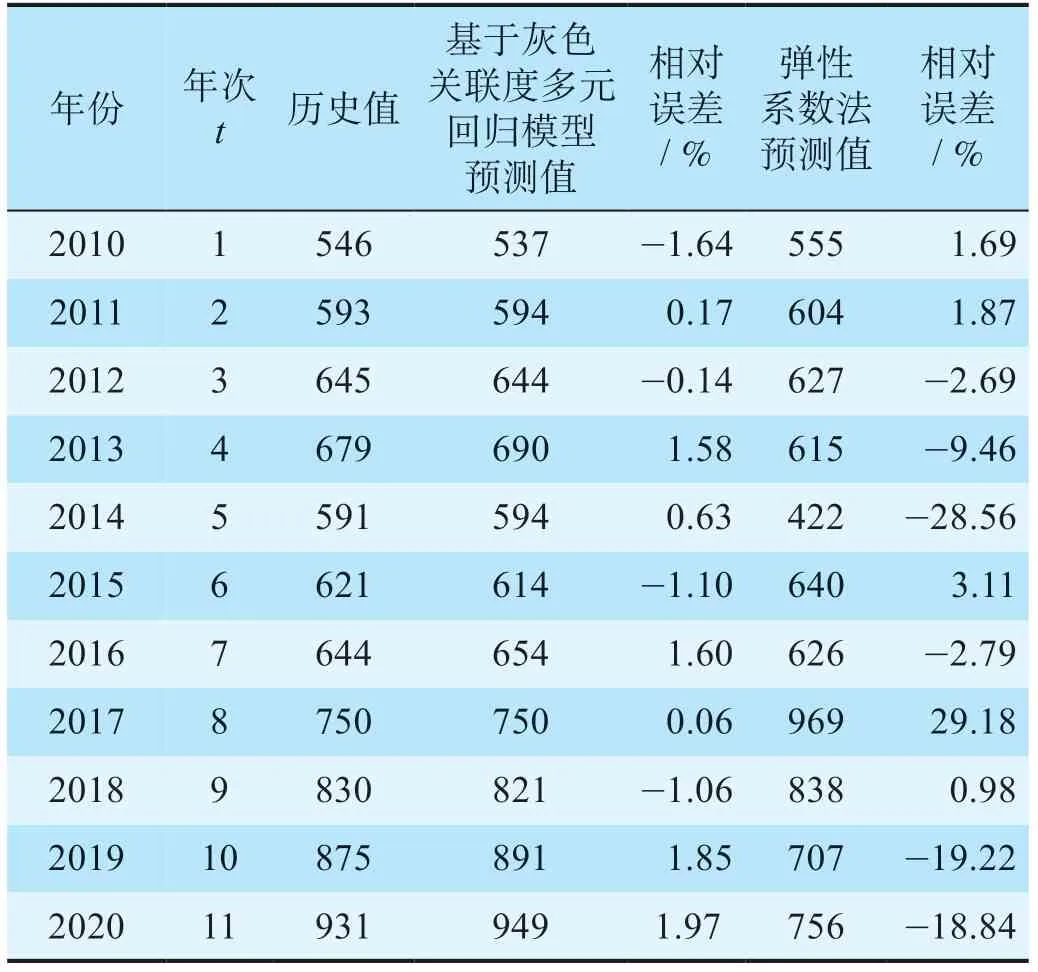
表5 基于灰色关联度多元回归模型预测值与弹性系数法 预测值误差分析Tab.5 Error analysis between the predicted value of multiple regression model based on grey correlation degree and that of elastic coefficient method

3.5 预测结果

（1）影响因子延伸性预测。以2009—2020年全国GDP为基础数据，建立全国GDP增长率的Gomperz成长曲线模型，预测2021—2030年的增长率，进而预测2030年全国GDP。2009—2020年全国GDP增长率预测模型计算如表6所示。

表6 2009—2020年全国GDP增长率预测模型计算表Tab.6 Calculation table of prediction model of national GDP growth rate from 2009 to 2020

利用公式(6)—(8)计算得出全国GDP增长率Gomperz成长曲线模型参数分别为f= 1.043，g= 0.744 0，ρ= 1.061 2。代入公式(5)全国GDP增长率Gomperz成长曲线模型如下。

根据公式(10)求得2021—2030年GDP增长率，进而分别计算2021—2030年全国GDP。同理可计算得出2021—2030年青岛市全社会物流量、山东省全社会物流量。关键影响因子2030年预测量如表7所示。

表7 关键影响因子2030年预测量 Tab.7 Prediction of key influence factors in 2030

（2）即墨铁路物流中心2030年运量。利用Gomperz成长曲线模型预测得出2021—2030年关键因子预测值，求得无量纲化序列值；进而带入基于灰色关联度多元回归模型公式 ⑼，可预测得出即墨铁路物流中心2030年预测运量。即墨铁路物流中心2030年运量预测如表8所示。

表8 即墨铁路物流中心2030年运量预测 万tTab.8 Traffic volume prediction of Jimo railway logistics center in 2030

即墨铁路物流中心运输需求重点集中在商品小汽车、钢铁、建材、木材、机械等品类。2020年分品类既有运量如表9所示。

表9 2020年分品类既有运量表 万tTab.9 Existing traffic volume by category in 2020

根据2030年运量预测值，结合既有分品类运量表，分析2030年即墨铁路物流中心分品类运量。分品类预测运量如表10所示。

表10 分品类预测运量表 万tTab.10 Traffic volume prediction by category

3.6 即墨铁路物流中心总平面规划

根据服务品类分析，物流中心以笨大货物作业用地、包件货物作业用地、集装箱货物作业用地、公路集散用地、综合仓储用地等用地为主，配套建设综合服务区。物流中心功能大区可划分为综合服务、公铁联运、公路集散、冷链物流、城市配送、综合仓储等功能区。结合文献分析[9]，根据不同货物的单位面积堆存量、存储周期、有效仓储面积等指标，结合预测运量计算各类用地及辅助设施用地面积。

（1）综合仓储用地。综合仓储用地= (入库货物年运量/年周转次数)×总入库系数/ (仓库内有效堆存面积×单位面积堆存量×建筑密度)。

（2）公路集散区用地。公路集散区用地包括停车用地、车间距和车辆通道等用地之和。计算公式为

式中：A车为停车场用地，m2；N到或发为每天到达或发送的车数，辆；k车为不平衡系数，可采用1.5 ~ 3.0；t门为每天门区作业时间，h；t待为车辆在物流中心平均等待的时间，h；F为每辆车投影面积，m2。

（3）堆场用地。堆场用地包括装卸作业所需通道、有效堆存货物用地、货物间距等用地之和，计算公式为

式中：A堆为堆场用地，m2；a为波动系数；Q为存放货物数量，t；t保管为保管期，d；P为单位面积堆存量，t/m2。

根据运量预测结果及相关标准计算功能区用地规模。即墨铁路物流中心各功能区用地规模估算值如表11所示。

根据货物进入园区、不同功能区间流转、运出物流中心的作业流程，引入动线分析的方法[9]，对各功能区间流转的货物量进行分析，根据各功能区间流转货物量的多少来衡量之间的关联关系；从组织管理、环境影响等方面来衡量各功能区之间的非物流关系；综合关联关系和非物流关系的分析统计，根据各功能区大小、各功能区关系紧密程度，结合可利用地的范围、用地性质、容积率等因素要求，对总平面进行布置。即墨物流中心功能区布置图如图1所示。

图1 即墨物流中心功能区布置图Fig.1 Layout of functional area of Jimo logistics center

4 结束语

随着国家交通运输结构调整，科学合理地规划铁路物流中心布局，打造现代化铁路物流基础设施对促进“公转铁”政策实施有积极意义。通过灰色关联度多元回归模型预测物流中心的运量，为物流中心的规划建设提供数据支撑，有利于合理确定物流中心的总体规模，优化物流中心功能布局，进而降低铁路物流中心建设成本；同时铁路物流中心的建设能够提高铁路货运产品的服务质量，提高市场竞争力，吸引更多的公路物流需求转向铁路，优化各种运输方式合理分工，降低企业的综合运输成本，进而促进区域各种运输方式的融合发展。