Discontinuous and continuous transitions of collective behaviors in living systems∗

Xu Li(李旭) Tingting Xue(薛婷婷) Yu Sun(孙宇) Jingfang Fan(樊京芳) Hui Li(李辉)Maoxin Liu(刘卯鑫) Zhangang Han(韩战钢) Zengru Di(狄增如) and Xiaosong Chen(陈晓松)

1School of Systems Science,Beijing Normal University,Beijing 100878,China

2Institute of Nonequilibrium Systems,Beijing Normal University,Beijing 100878,China 3School of Science,Beijing University of Posts and Telecommunications,Beijing 100876,China

Keywords: living systems,phase emergence,phase transitions,eigen mircostate

1. Introduction

Collective behaviors are the most important properties of systems consisting of many individuals. Collective motion of large groups of individuals is a truly fascinating collective behavior in living systems and was observed in starlings,[1–3]bacterial communities,[4,5]ant colonies,[6,7]locusts,[8]midges,[9,10]sheep,[11]etc. While detailed case studies are preferred in general by biologists,[8,12,13]physicists usually seek for universal features behind seemingly diverse observations and the models sufficient to capture the fundamental features[14]to find the fundamental principles of collective motion.

It is the mission of statistical physics to connect the microscopic properties of individual with the macroscopic behavior using the probability theory and statistics.[15–17]In addition, the studies of phase transitions and critical phenomena[18]need to identify order-parameters in advance.

As a prototype model of collective motion in living systems,the standard Viscek model(SVM)[19]was introduced.In the original work of SVM,it was claimed that phase transition of collective motion is continuous. But this was challenged later by Chat´eet al.[20,21]They showed that the continuous nature observed is actually due to finite-size effects and the phase transition is discontinuous. Since the precise order-parameter of collective motion is unknown and no systematic analysis of finite-size scaling has been made, these results about the nature of phase transitions until now are not conclusive.

In an eigen microstate approach developed recently,[22,23]collective behaviors of systems are indicated by the condensation of eigen microstate in statistical ensemble,[24]which is analogous to the Bose–Einstein condensation of Bose gases.[25]The approach has been applied successfully to study the phase transitions of Ising models.[22,23]Here we use this approach to investigate collective behaviors of living systems and identify order-parameters and the nature of phase transitions precisely.

2. Eigen microstates and phase transitions

2.1. Microstates

For a particleiof a living system,its state is characterized by velocityvi(t)and positionxi(t).It is more relevant to introduce neighborhood density ofiasni(t)=Ni(t)/(2r)2, whereris the interaction distance andNi(t)is the number of the particles aroundiwithin a square with side length 2r. From states ofNcomponents att=1,2,...,M,we can obtain the average velocity and neighborhood density as

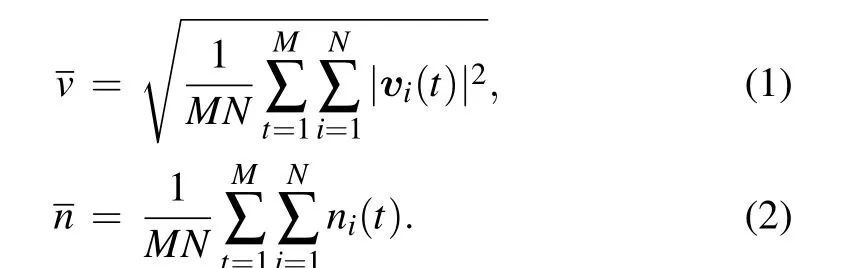
2.2. Eigen microstates[22]

UsingMmicrostates of the living system, a statistical ensemble[24]can be composed and characterized by anNT×MmatrixAwithNT=3Nand elements[22]

2.3. Phase emergence

If a probability amplitudeσI →no-zero at the limitsM →∞andN →∞, there is a condensation of the eigen microstateuIin the statistical ensemble. This condensation of eigen microstate is analogous to the Bose–Einstein condensation of Bose gases,[25]in which a finite part of total bosons simultaneously occupy the ground state. This condensation of eigen microstate implies an emergent phase described byuI.More than one emergent phase can exist in a system.

2.4. Phase transition and finite-size scaling

With changes of external conditions or internal conditions of living systems, a probability amplitudeσImay increase from zero to finite. Now there is a phase transition with orderparameter described byσIand new phase characterized byuI.

With external conditions characterized by a parameterη,we haveη=ηcat the phase transition point. The distance from the phase transition point ish= (η −ηc)/ηc. In the asymptotic region with|h|≪1,we proposed a finite-size scaling form ofσIas[22]

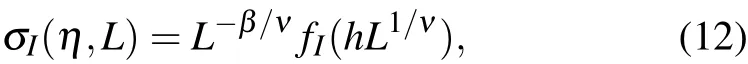
whereLis the system size,βis the critical exponent of order parameter,andνis the critical exponent of correlation length.

Forβ> 0, we haveσI(η,∞) = 0 atη>ηcandσI(η,∞)∝(ηc−η)βforη<ηc. This is a continuous phase transition.

Whenβ=0,there is a jump fromσI(η,∞)=0 atη>ηctoσI(ηc,L)=fI(0)/=0 atηc. This indicates a discontinuous phase transition.

2.5. Global indexes of eigen microstate

To get an overview ofuI,we define the collective motion index as

2.6. Spatial distribution of eigen microstate

We have applied the eigen microstate approach(EMA)to study successfully the ferromagnetic phase transitions of Ising models in equilibrium.[22]Here the EMA is used to investigate the emergent phases and their phase transitions of nonequilibrium living systems.

3. Results and discussion

3.1. SVM[19]

In a two-dimensional SVM, there areN=L×Lpointwise particles labeled as 1,2,...,Nand placed randomly on a two-dimensional domain with sizeLand periodic boundary conditions. They move synchronously at discrete time steps by a fixed distancev0∆t, wherev0is the velocity defined as the length of displacement per time step ∆t=1. Each particleiis endowed with an angleθithat determines the direction of the movement during the next time step,and its update is determined by the orientations of its neighbors(defined as particles within a unit circle centered around particlei,including itself).The influence of the neighbors is through an average angle

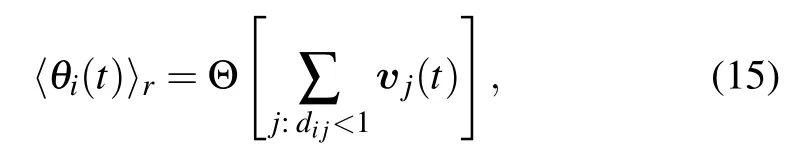
where Θ[v]represents the angle of vectorvanddijis the distance between particlesiandj. The evolution is

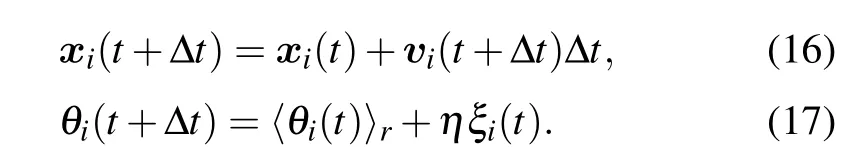
Here the key ingredient is the competition between the tendency towards local alignment and the angular noiseξi(t)that might come from external perturbations and/or from uncertainties in individual’s perception, chosen from a uniform distribution within the interval[−1/2,1/2]. The amplitude of noiseηhas a maximum valueηmax=2π. In the absence of noise withη=0,all particles tend to align perfectly.

For SVM,v=v0, ¯vi,x=cosθi,and ¯vi,y=sinθi. Our simulations are started with all particles distributed randomly in the domain. To overcome the dependence on the initial conditions,the first 2×105microstates are neglected. The subsequent microstates are chosen at an interval of 40 steps to keep independence. We takeM=2×104microstates to get an ensemble matrixA.Its eigenvalues and eigen microstates can be calculated afterwards.

Fig.2.Log–log plot ofWEI versus L around transition points.(a)WE1 with η1c=3.95 and β1/ν1=−0.0000(5).(b)WE2 with η2c=3.69 and β2/ν2=0.94(1).(c)WE3 with η3c=3.69 and β3/ν3=0.94(2).

The probabilities of the eigen microstates are presented in Fig. 1. Under strong noises, no eigen microstate is dominant and the system is in disorder. With the decrease ofη,σ1becomes finite and a phaseu1emerges at first. Further,two degenerate eigen microstatesu2andu3appear simultaneously.

Fig.1. Probabilities WEI of eigen microstates in SVM with ρ =2,v0=0.5.(a) Different probabilities at L=32. (b)WE1 at different sizes. (c)WE2 at different sizes. (d)WE3 at different sizes. The phase transition point of u1 is indicated by the black arrow and that of u2,3 by the red arrow.

To identify the phase transition point and type of phase transition, we investigate the size dependence ofWEI(η,L).According to Eq.(12),we have

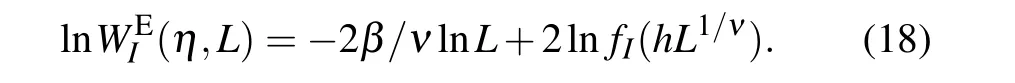
There is a linear dependence of lnWEIon lnLath=0.This can be used to determine the transition point and critical exponent ratioβ/νat the same time.

It has been manifested in Fig.2(a)thatWE1has a jump atη1c=3.95, which indicates a discontinuous phase transition ofu1. In Figs.2(b)and 2(c),a continuous phase transition ofu2andu3atη2c=3.69 is identified. It has the ratio of critical exponentβ/ν=0.94.

To characterize the physical character of the phase transitions above,we calculate the collective motion index and density fluctuation index of eigen microstate and present them in Fig.3. In the eigen microstates,velocity and density are correlated. This is similar to the magnetic lattice gas,[28]where the orientation and density of the particle are correlated.

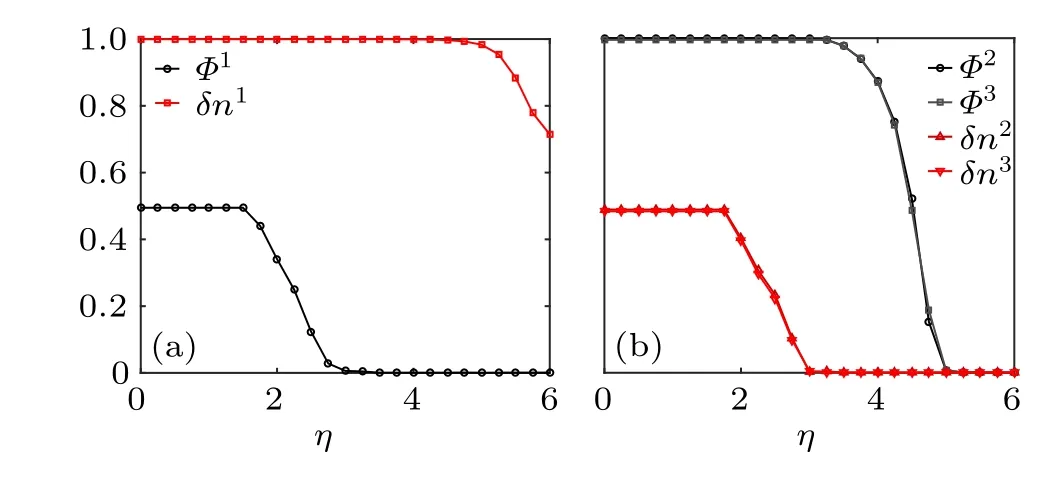
Fig. 3. Collective motion index ΦI and density fluctuation index δnI of SVM with size L=64. (a)I=1. (b)I=2,3.

Atη1c,u1has zero collective motion indexΦand nonzero density fluctuation indexδn. Therefore,u1has a discontinuous transition of density. Atη2c,bothu2andu3have nonzeroΦand zeroδn. Here there is a continuous transition of velocity.

The spatial distributions of eigen microstates are shown in Figs.4 and 5 foru1andu2,respectively. In Fig.6,the velocities and density fluctuations of eigen microstatesu3are shown for different noises. The velocity direction ofu3is orthogonal to that ofu2.

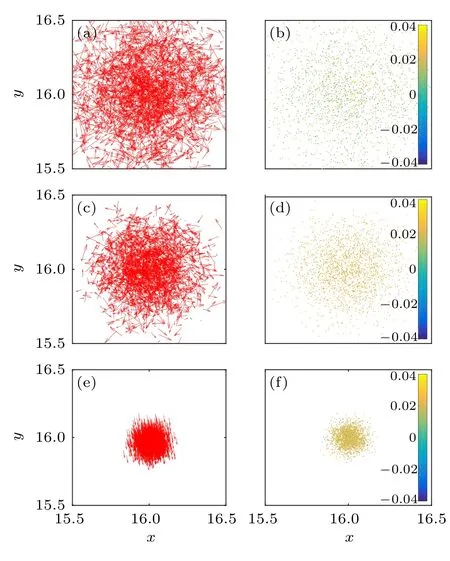
Fig.4. Spatial distributions of velocity(a), (c), (e)and neighborhood density fluctuation(b),(d),(f)for u1 under noises η =6,η1c=3.95,and 0.25 respectively.

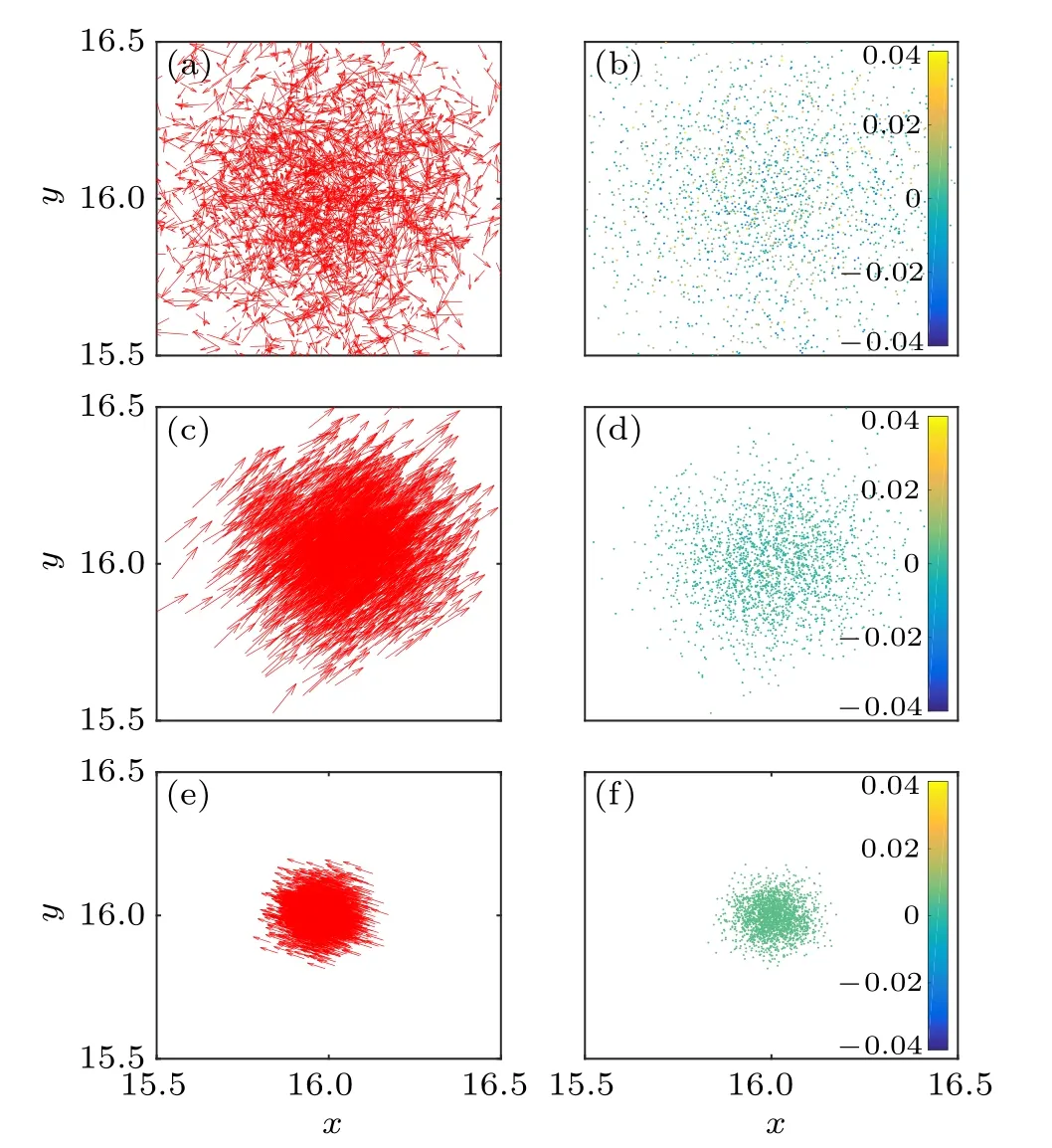
Fig. 5. Spatial distribution of velocity (a), (c), (e) and neighborhood density fluctuation(b),(d),(f)for u2 under noises η =6,η2c=3.69,and 0.25 respectively.

Fig.6. Spatial distribution of velocity(a),(b),(c)and neighborhood density fluctuation(d),(e),(f)for u3 of SVM under noises η =6, η3c =3.69 and 0.25. The velocity direction of u3 is orthogonal to that of u2.

Fig.7. Average particle densityn as a function of noise.

To investigate the density dependence of the phase transitions,we study also the SVM at densitiesρ=1,3 in addition.There are also discontinuous phase transitions of density at first and then continuous phase transitions of velocity in these systems. With the increase of density,the discontinuous transition of density appears at larger noise. We have obtainedη1c=3.18 atρ=1,η1c=3.95 atρ=2, andη1c=4.3 atρ=3. As shown in Figs. 2, 9, and 10, the jump of orderparameter decreases with increasing density.

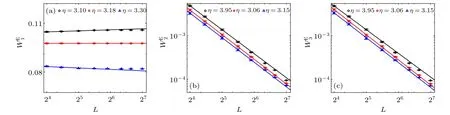
Fig.9. Log–log plot of WEI versus L for SVM with ρ =1. (a)WE1 with η1c=3.18 and β1/ν1=−0.0001(7). (b)WE2 with η2c=3.06 and β2/ν2=0.94(3).(c)WE3 with η3c=3.06 and β3/ν3=0.93(9).

Correspondingly, the continuous transition pointsη2c,3cincrease with increasing density.We getη2c,3c=3.06 atρ=1,η2c,3c=3.65 atρ=2, andη2c,3c=4.0 atρ=3. The same ratio of critical exponentβ/νhas been obtained for the different continuous phase transitions,which belong to the same universality class.

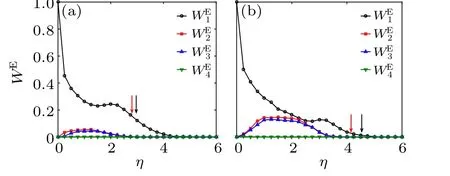
Fig.8. Probabilities of the first four eigen microstates for SVM with L=32 and densities (a) ρ =1, (b) ρ =3 (b). The phase transition point of u1 is indicated by the black arrow and that of u2,3 by the red arrow.

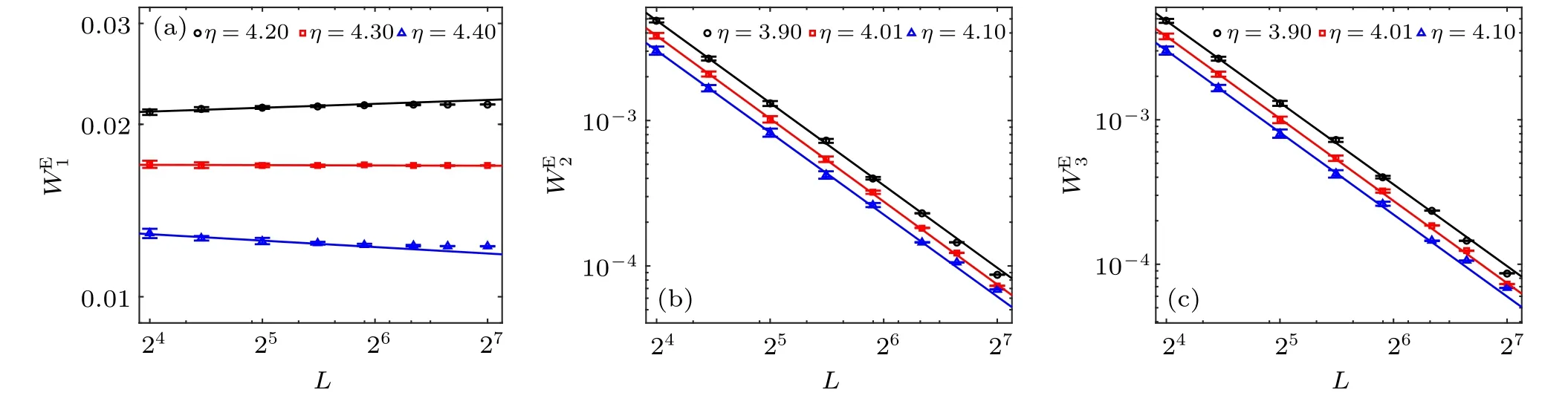
Fig.10. Log–log plot of WEI versus L for SVM with ρ =3. (a)WE1 with η1c=4.3 and β1/ν1=0.0001(7). (b)WE2 with η2c=4.01 and β2/ν2=0.94(3).(c)WE3 with η3c=4.01 and β3/ν3=0.94(1).

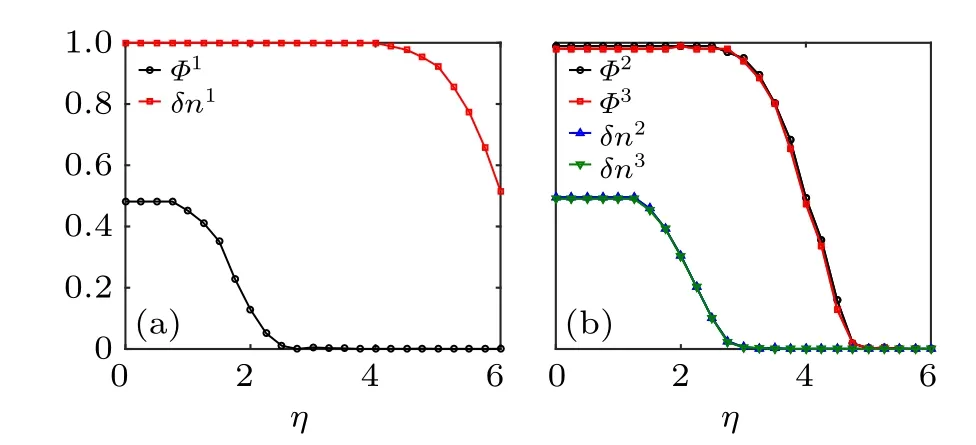
Fig. 11. Collective motion ΦI and density fluctuation δnI of SVM with L=32 and ρ =1.

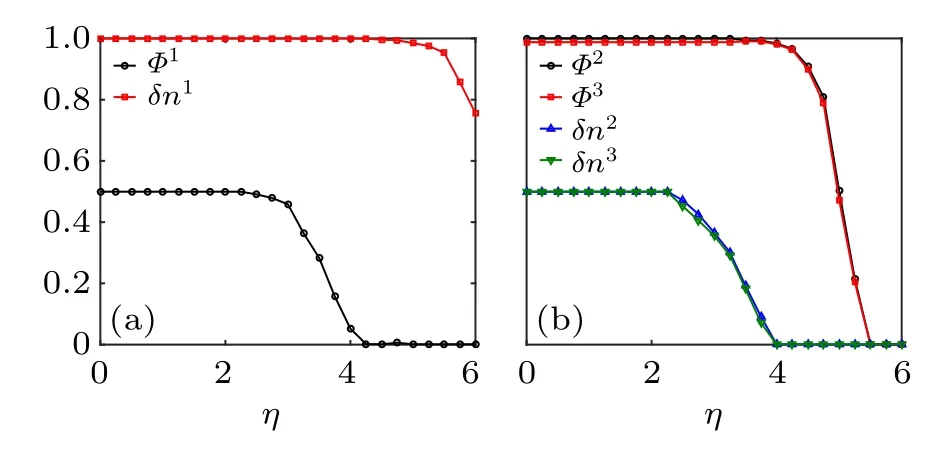
Fig. 12. Collective motion ΦI and density fluctuation δnI of SVM with L=32 and ρ =3.

To explore the generality of the phase transitions found in SVM, we study the hierarchical Vicsek model (HVM),[30]which is a generalized version of SVM.

3.2. HVM

In the HVM,all particles are ordered by their hierarchical rankjwithj=1 being the highest andj=Nthe lowest. For particlei, the influence of a lower-ranked particlej ≤iis reduced by a factorα<1. Instead of Eq.(10),the average angle here is

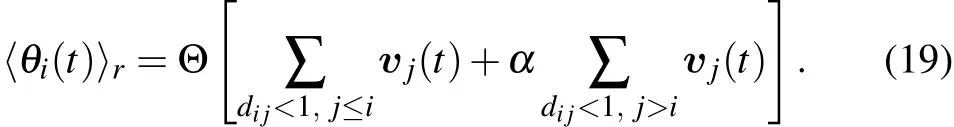
SVM is recovered byα=1.

We have studied the HVMs atα=1/9,1/36. In Fig.13,the probabilities of the first four eigen microstates are presented forα=1/9 in (a) andα=1/36 in (b). Their transition points are determined in Figs. 14 and 15 and indicated by arrows. With the decrease ofα,the peaks ofWE1andWE2,3increase.

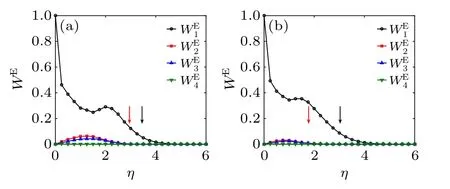
Fig.13. Probabilities of HVM with L=32,ρ =2 and hierarchical factors:(a)α =1/9,(b)α =1/36. The transition points are indicated by arrows.

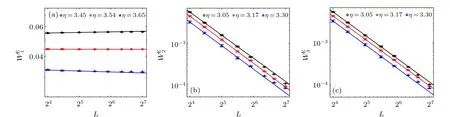
Fig. 14. Log–log plot of WEI versus L for the HVM with α =1/9. (a) WE1 with η1c =3.54 and β1/ν1 =−0.0000(1). (b) WE2 with η2c =3.17 and β2/ν2=0.94(4). (c)WE3 with η3c=3.17 and β3/ν3=0.93(8).

Fig. 15. Log–log plot of WEI versus L for the HVM with α =1/36. (a) WE1 with η1c =3.23 and β1/ν1 =−0.0000(3). (b) WE2 with η2c =2.3 and β2/ν2=0.94(2). (c)WE3 with η3c=2.3 and β3/ν3=0.94(1).

Because of the hierarchical rank in HVM, the discontinuous phase transition ofu1is delayed by the hierarchical factorαso thatη1c= 3.95 forα= 1,η1c= 3.54 forα= 1/9, andη1c= 3.23 forα= 1/36. Correspondingly,the jump at the discontinuous transition of density increases asWE1(η1c,L)=0.035 atα=1,WE1(η1c,L)=0.043 atα=1/9,andWE1(η1c,L)=0.060 atα=1/36.

The continuous phase transitions of HVM are also delayed so thatη2c,3c=3.65 atα=1,η2c,3c=3.17 atα=1/9,andη2c,3c=2.3 atα=1/36. The ratiosβ/νat differentαare the same. So the continuous phase transitions of SVM and HVM belong to the same universality class. We summarize the results obtained above in Table 1.

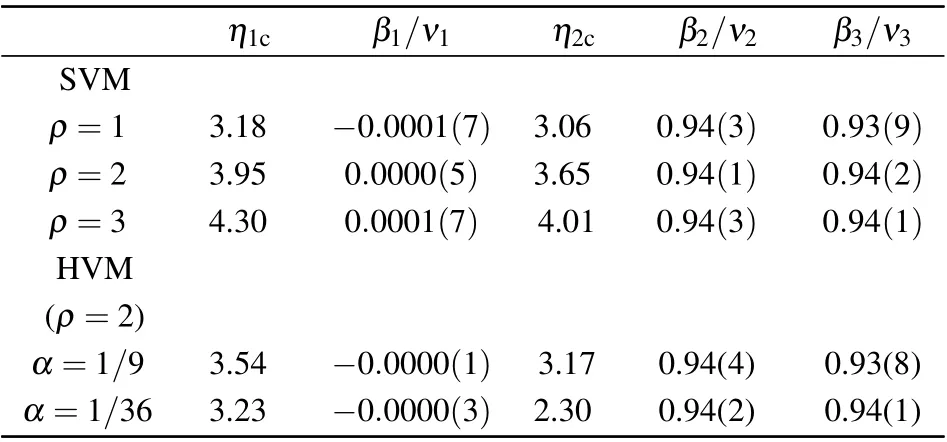
Table 1. Summary of transition points and ratios of critical exponents.

Our studies above show that particles in the living systems with strong noise have random positions and velocities.With the decrease of noise,the interactions between the particles make them get closer and the average density ¯nbecomes larger, as shown in Fig. 7. These interactions result in a gasliquid like transition of density,which is discontinuous. With further decrease of noise, particles stay further closer to each other and the average density ¯nbecomes larger. The even stronger interactions between particles make the directions of velocity become ordered and there is a phase transition of collective motion,which is continuous.

4. Conclusions

We propose a method for investigating phase emergence and transitions in living systems under the framework of eigen microstate. From the velocity and position sequences of particles in a living system,we define a normalized ensemble matrixAwith columns and rows corresponding to microstates and time sequences of the particles.Acan be decomposed as the sum of eigen microstateuImultiplied by its time sequencevIand eigen valueσI, where ∑I σ2I=1. A finiteσIin the thermodynamic limit reveals the emergence ofuI. Near transition pointh= 0,σIfollows a finite-size scaling formσI(h,L)=L−β/ν fI(hL1/ν),withβ>0 andβ=0 for continuous and discontinuous phase transitions,respectively.

The phase emergence and transitions of both SVM[19]and HVM[30]have been investigated. With the decrease of noise,we find at first phase emergence of density withβ=0. So the corresponding phase transitions are discontinuous. At even smaller noises, there is the phase emergence of velocity withβ/ν=0.94 and the phase transitions are continuous and belong to the same universality class.

Our results demonstrate that the eigen microstate approach works for nonequilibrium systems. Our approach can be applied not only to living systems but also to other complex systems,such as climate systems,[23,31]ecosystems,[32]et al.

Acknowledgment

We thank Profs. Li Chen and Xiaqing Shi for helpful discussions.