基于MATLAB与CATIA的渐开线斜齿轮精确快速建模方法研究

葛德，徐飞，林勇

（无锡商业职业技术学院机电技术学院，江苏无锡 214153）

0 引言

齿轮传动是近代机器中最常见的一种机械传动，是传递机器动力和运动的一种主要形式。斜齿轮因其在传动中传动平稳、噪声小、承载能力高等特点而被广泛使用。CAD环节则是整个CAX流程的基础，对于形状复杂的斜齿轮精确快速建模及后续方案修改，通过三维设计软件平台变量与参数的混合建模可轻松实现，大幅缩短产品设计周期。本文在对斜齿轮深入研究基础上，指出一种现有建模方法上的错误思路，并提出一种基于MATLAB和CATIA多平台环境下的斜齿轮快速精确建模方法。

1 渐开线齿轮的形成原理

1.1 齿轮渐开线的形成原理

如图1所示，当一条直线MN沿半径为rb的圆周作纯滚动时，其直线上任意一点M的轨迹PM就是该圆的渐开线。在直角坐标系下，动点M轨迹方程为：

图1 渐开线生成原理

式中：θ为渐开线发生线的滚动角，θ=θk+αk；θk为渐开线展角；αk为渐开线压力角。

1.2 斜齿轮齿面的形成原理

图2所示为斜齿齿轮形成原理图，由图可知，当发生面BB″T′t沿半径为rb的基圆柱作纯滚动时，发生面上直线BB′所展出的渐开面BB″A′A为直齿轮齿廓曲面。斜齿轮齿廓曲面的形成与直齿轮类似，只是发生面上的直线与轴线不再平行，而是与基圆柱轴线成一角度βb，即斜直线BB″的运动所展出的曲面BB″A″A为斜齿轮的齿廓曲面。渐开曲面BB″A″A与基圆柱的交线AA″是一条螺旋线，螺旋角为βb，故斜齿轮的齿廓曲面为渐开螺旋面。

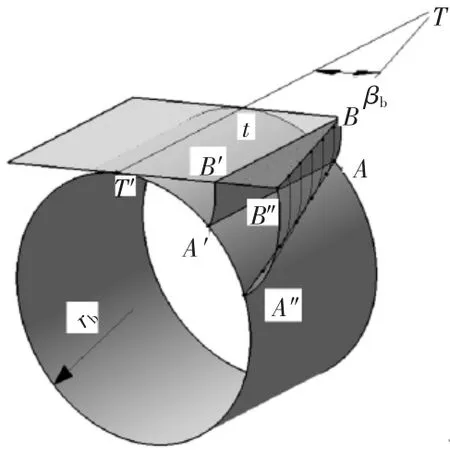
图2 斜齿齿轮面形成原理

2 基于CATIA建模分析

2.1 建模方法分析

国内部分学者基于CATIA进行渐开线斜齿轮参数化建模时，一般是以直齿轮齿廓为基础，按照螺旋角β进行三维拉伸，在CATIA中建立基本参数连接相关公式绘制若干点对应坐标[1-3]。其中在β的定义过程中有两种思路：一是以建立螺旋线参数方程生成螺旋曲线为路径，进而完成斜齿轮实体建模；二是以按照螺旋角β定义通过投影获得所需螺旋角，生成实体建模。在此过程中主要存在以下几点问题：

1）在CATIA中，由于渐开线是以样条曲线联接参数方程生成若干关键控制点所形成，点数数量有限且绘制不精确，样条曲线与理论廓线差距较大，齿廓精度无法保证，最终影响数值模拟分析。这也是困扰广大科研工作者的一大核心问题。

2）轮齿齿廓渐开线展角θk没有固定值，通常选取θk>>[θa]（轮齿齿廓展角），以避免在更改齿轮参数时，因渐开线长度不够而出现错误。在θk取值一定的情况下，所绘制渐开线精度与控制点数成正相关，精度越高所需点数越多，生成数据也就越庞大。

3）在进行实体成形时，有相关技术人员采用的参考β以投影方法，将一平面上的与齿轮轴线夹角成β斜线投影到分度圆圆柱面，这并非按照斜齿轮螺旋角β的定义——展开（纯滚动）进行，最终齿轮的螺旋角β′≠β，而应通过建立以螺旋线参数方程生成螺旋曲线做为螺旋角β。

基于上述问题分析，在CATIA进行斜齿轮参数化建模时，轮齿齿廓会产生多元偏差，在进行有限元仿真分析时，会产生较大误差。

2.2 改进方案

利用MATLAB GUI进行渐开线齿廓的绘制并生成可控关键点，通过宏运算将可控关键点导入CATIA，进而在CATIA中完成三维实体建模。该方案有如下优势：

1）渐开线绘制的高效性。通过程序编译自动生成渐开线关键点及相应坐标，利用宏运算将点云数据批量导入CATIA环境中，免去在CATIA中手动输入并编辑点的工作，同时保证了渐开线的精度。

2）轮齿齿廓最大展角θk具有自适应性。在生成渐开线的程序中通过设置方程约束，确定了θk边界条件，生成的渐开线即为有效渐开线，且轮齿齿廓展角θa会随齿轮参数更改而自行更新，实现了渐开线的精确自动绘制，生成的数据简洁有效。

3）螺旋角β具有较高的可靠性。进行肋特征的参考β按照螺旋角的定义，通过展开特征获得，并非通过投影获得（具体内容见下文），这就保证了齿轮螺旋角β的正确性。

3 渐开线斜齿轮参数化建模实例

现以某新型汽车变速箱行星齿轮为例，基于MATLAB进行交互界面程序开发，在CATIA环境下进行斜齿轮的参数化建模，相关参数指标如表1所示。

表1 某新型汽车变速箱行星轮部分参数

3.1 渐开线展角θk边界条件

由图1及渐开线方程可知，渐开线在向径为rk处的展角θk为

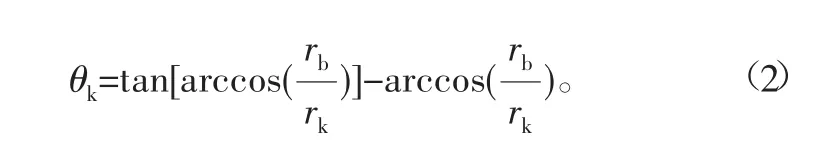
由图3可知，在标准渐开线齿廓当中，齿顶圆与渐开线有且仅有一交点k，OK为标准齿轮齿廓渐开线最大向径rk，由几何关系知：

图3 齿轮齿廓渐开线曲线

式中：α为标准渐开线齿轮压力角，取定值20°；z为标准渐开线齿轮齿数；[θa]max为最大齿廓展角。

式（3）表明：渐开线标准齿廓展角θa大小仅与齿数z有关，与模数m无关，因此标准齿轮齿廓渐开线展角θk的边界条件为[0,θa]。

3.2 基于MATLAB GUI及CATIA联合建模过程

本文利用MATLAB 开发渐开线曲线设计平台，通过输入相关参数，生成渐开线曲线图形，最后导出点云数据。所开发的软件界面如图4所示。

图4 标准齿轮渐开线曲线参数化设计平台界面

程序主窗口包含方程显示区、参变量输入区、图像显示区、命令区。预设参变量缺省值为0，通过更改控制取样点数可以达到控制渐开线精度的目的。以行星齿轮为例，通过输入表1中相关参数，生成的曲线为二维曲线，在保存点云数据时，软件会自动填补曲线第三维坐标为0。将保存的三维点云坐标通过宏运算将点云数据批量导入CATIA环境中，生成渐开线曲线如图5所示，图中所示取样点数为100。在CATIA环境下生成一个带参标准渐开线齿轮的端面几何图形，如图6所示。

图5 基于MATLAB GUI与CATIA GSD环境下实现渐开线绘制

图6 全齿端面几何图形

3.3 螺旋角β的分析与绘制

通常在CATIA中进行三维特征创建时，所采用的螺旋角β为投影方法得到，而应用此方法所得到的螺旋角β已不是斜齿轮所用的螺旋角β，即采用投影法绘制的图形是错误的。

在一般情形下，已知基圆半径rb，渐开线上K点处坐标（Kx，Ky）（Kx≠0），建立一般情况下的直角坐标系如图7（假设图示点均位于第一象限）所示。

图7 渐开线通用坐标系

设M、B、A 三点坐标分别为（Mx，My）、（Bx，By）、（Ax，Ay），则有：

如图8所示，已知rb=10 mm，K点坐标为(4,11)，按照式（4）～式（6），得M、B、A三点坐标分别为M（3.417 436,9.397 934）、B（7.803 677,6.253 208）、A（2.830 540,9.591 037），通过验证，上述推理完全正确，即论证了投影与展开的区别。图9为采用展开方法建立的齿轮数模。

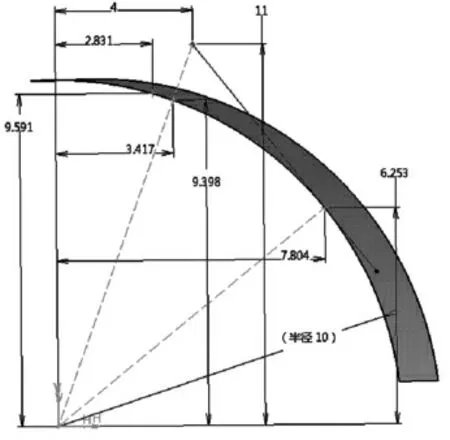
图8 投影与展开验证

图9 渐开线斜齿轮三维数模图

3.4 螺旋角β的验证

为对所建立的斜齿轮模型准确性进行验证，按照螺旋线的定义，将生成的三维实体随机取样，用于验证斜齿轮螺旋角β的正确性。如图10所示，各取样点处的螺旋角度均为β，所建数模符合要求。图11为随机更改齿轮相关参数（z=30、β=8°）获得的齿轮数模，数模随参数变化而自动更新，表明建模思路方法是切实可行的。

图10 行星轮某齿各取样点下螺旋角β值

图11 更改齿轮参数后数模及螺旋角β

4 结语

1）分析了在利用CATIA进行斜齿轮数字化建模时，易出现的几点缺陷及产生原因，并提出相对应解决方案。

2）分析并得出了渐开线齿轮渐开线展角与齿轮基本参数之间函数的关系，并基于上述成果实现了基于MATLAB的可用于生成标准直齿轮渐开线曲线的可执行程序开发，提高了渐开线绘制精度和效率。

3）分析了CATIA曲面建模中，投影与展开命令的原理，得出各点坐标推导关系，指出并纠正了一种斜齿轮螺旋角β的绘制思路方法。

4）实现了基于MATLAB与CATIA的渐开线标准斜（直）齿轮参数化建模方法，为齿轮传动系统的快速三维实体建模及后续相关仿真分析奠定基础。