不同入渗模型对LID措施效能评价的影响研究
葛有成, 唐双成, 单正清, 许 青, 赵文宇, 陈 锋
(1.扬州大学 水利科学与工程学院, 江苏 扬州 225009; 2.南通市通州区金沙街道水利站, 江苏 南通 226300)
1 研究背景
近年来,随着城市化进程的加快,硬化的不透水下垫面极速扩张,使得地表径流的汇集时间缩短、径流峰值流量和总量骤增,直接引发了城市洪涝频发和水生态恶化等问题[1-2]。而采用单一的径流快速排除模式,通过提高排水管网的设计标准无法彻底地解决城市内涝问题,还转移了本可以补给地下水的雨水资源,与区域开发前的原有水文机制不相符[3]。又因城市雨水径流具有随机性强、分布面广等特点,低影响开发(low impact development, LID)雨水管理理念开始在世界各地逐步地被接受并推广[4-5]。LID理念摒弃以往对径流的快速排除机制,强调通过源头控制、过程管理以及末端调蓄措施维持和保护场地天然的水文功能,有效缓解快速城市化引发的洪涝灾害频发和污染加剧等问题[6-8]。2013年,我国提出建设“自然积存、自然渗透、自然净化”的海绵城市,LID措施是海绵城市理念的核心源头控制措施[9-11],随着海绵城市建设的推广,国内针对LID措施的研究与应用逐步深入。
随着雨水花园、透水铺装[12-13]等各种LID措施的广泛应用,有关LID措施滞蓄入渗能力的研究也不断得以深入。侯精明等[14]采用SWMM(storm water management model)模型内嵌的Horton模型模拟了在不同土壤条件下,LID措施对径流调控效果的影响,结果表明,LID措施在饱和状态和半饱和状态下的径流削减能力明显小于自然状态下的径流削减能力。唐双成等[13]采用平均入渗率来研究雨水花园的滞蓄能力,结果表明,雨水花园在入渗率和设计深度一定时,溢流时间与汇流面积比及雨强有关。石宝山等[15]研究了基于Green-Ampt和稳定入渗两种不同模型下的城市内涝模拟,结果表明,相对于稳定入渗模型,Green-Ampt在频率为1、10、50 a的降雨条件下,内涝积水分别减少28.41%、21.04%、15.02%,模型模拟结果受降雨强度影响变化更加明显。随着海绵城市理念的发展与相关研究的愈加深入,各种不同入渗模型被广泛地应用于LID措施设计和效能评价中。相关规范[16]及一些研究对于入渗量的计算常采用稳定入渗模型,基于SWMM模型的城市雨洪研究中普遍使用了模型自带的Horton入渗模型[14,17],还有学者在城市雨洪的研究中尝试了Green-Ampt模型[15]。但在LID措施设计和效能评价时,不同入渗模型之间的差异性研究还相对较少。
稳定入渗模型和Horton模型是经验模型,Green-Ampt模型是半经验半理论模型,采用不同入渗模型计算LID措施的滞蓄效果存在一定差异。本文采用MATLAB编程建立LID措施的水量平衡计算模型,入渗过程选择稳定入渗模型、Horton入渗模型和Green-Ampt入渗模型并基于扬州市土壤实测数据,对比分析在不同雨强、不同前期土壤含水率情况下该3种入渗模型计算LID措施滞蓄能力的差异,并讨论不同入渗模型的特点和适用范围,研究结果可为LID措施的精确设计提供参考依据。
2 模型建立与评价
2.1 模型建立
2.1.1 稳定入渗模型 稳定入渗模型设定一恒定入渗率is,土壤含水量达到了饱和含水量时,入渗率为最小值,土壤入渗率近似为常数,对应的累积入渗量Ws计算式如下:
Ws=is·A·T+H·A
(1)
式中:Ws为累积入渗量,cm·m2;is为稳定入渗率,cm/min;A为LID措施面积,m2;t为入渗持续时间,min;H为LID措施表层蓄水深度,cm。
2.1.2 Horton入渗模型 Horton模型的入渗率由初始入渗率、稳定入渗率和折减系数决定。土壤含水量直接影响其入渗性能,随着降雨历时的延长,深部土体的含水率增大,入渗率逐渐减小,入渗达到稳定[18]。Horton入渗公式依据入渗率随时间变化建立如下经验方程:
ih(t)=is+(i0-is)e-βt
(2)
式中:ih(t)为Horton模型t时刻瞬时入渗率,cm/min;is为稳定入渗率,cm/min;i0为初始入渗率,cm/min;t为入渗持续时间,min;β为折减系数。
将公式(2)对时间t进行积分,得到累积入渗量Ih的表达式:
(3)
式中:Ih为Horton模型累积入渗量,cm·m2。
2.1.3 Green-Ampt入渗模型 Green-Ampt入渗模型假设土壤剖面中存在一个很陡的湿润峰面,湿润峰面到土壤表面的土壤为饱和区,饱和区为恒定的饱和含水率θs,同时湿润峰处土壤吸力Sf固定不变;湿润锋之下的土壤为干土区,干土区均为初始土壤含水率θ0[19-20]。根据达西定律,可以推导出入渗率为:
(4)
式中:ig为Green-Ampt模型瞬时入渗率,cm/min;Ks为土壤饱和导水率,cm/min;θs为土壤饱和含水率;θ0为土壤初始含水率;Sf为土壤湿润峰平均水吸力,cm;I为累积入渗量,cm·m2。
为解决公式(4)中ig只有隐函数解的问题,Philip于1985年提出了大毛管特征长度(L)概念,或者称为临界压力或半吸力长度。张振华等[21]利用该概念推求了Green-Ampt模型入渗率显式近似解,利用公式(4)得出入渗率ig和入渗量Ig的表达式:
(5)
(6)
式中:Δθ为土壤含水率变化量;b为介于0.5~π/4之间的常数,其值取决于土壤水扩散率函数的形状;Ig为Green-Ampt模型累积入渗量,cm·m2。
2.1.4 溢流时间确定 假设为平均雨强条件,则降雨历时内的总入流量为:
Wr=μ·T·R·A(B+1)
(7)
式中:Wr为入流量,cm·m2;R为平均雨强,cm/min;T为入流持续时间,min;B为汇流面积比;A为LID措施面积,m2;μ为径流系数。
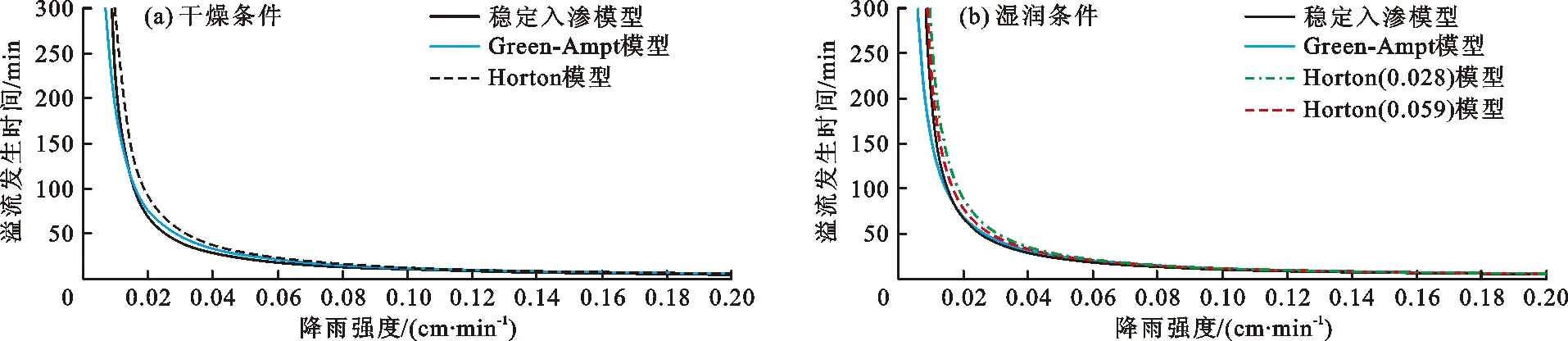
LID措施面对设计降雨时,正好未发生溢流,此时,入流量Wr等于总滞蓄水量Wx,溢流发生时间点t等于入流持续时间T。求解溢流发生时间点t对LID措施设计以及LID措施滞蓄能力评价至关重要。当t>T时,LID措施未产生溢流,则有Wx=Wr。当t Wx=I+A·H (8) 式中:Wx为总滞蓄水量,cm·m2;I为累积入渗量,cm·m2;H为LID措施的蓄水深,cm;A为LID措施的面积,m2。 基于以上理论公式,得出不同入渗模型对应的溢流发生时间t的计算公式,如表1所示。 表1 不同入渗模型的溢流发生时间t计算公式 模型的精度是衡量可靠性的重要指标,本文采用相关指数R2作为评估模型拟合可靠程度的指标,计算过程中采用平均绝对误差(mean absolute error,MAE和平均相对误差(relative error,RE)两个指标将不同模型的入渗率拟合误差量化,作为比较模型之间入渗率误差大小的依据,具体计算公式如下: (1)相关指数(R2)。 (9) (2)平均绝对误差(MAE)。 (10) 式中:xi为实测值;x为模拟值;n为样本个数。 (3)平均相对误差(RE)。 (11) 为研究选用不同入渗模型对LID措施蓄渗效果计算的影响,依据扬州地区积水入渗实验实测的入渗过程,基于两种不同初始入渗率的干湿条件,使用MATLAB软件拟合,确定稳定入渗模型、Horton入渗模型以及Green-Ampt入渗模型在不同土壤含水率状况下的对应计算参数值。干燥条件的初始入渗率为0.25 cm/min,湿润条件的初始入渗率为0.15 cm/min。 图1为扬州地区土壤实测入渗率变化过程。由图1可知,入渗率随入渗历时逐渐减小,约1 h后,入渗率稳定在0.05 cm/min左右,入渗过程进入稳定入渗阶段,因而取稳定入渗率为0.05 cm/min。拟合Horton和Green-Ampt两种模型时,依照干燥、湿润两种条件下的不同初始入渗率分别拟合。 图1 扬州地区土壤实测入渗率变化过程 在干燥与湿润条件下分别对Horton模型和Green-Ampt模型进行拟合, 图2为该两个模型分别在干燥和湿润条件下的入渗率随入渗历时变化过程拟合结果与实测值比较。折减系数β为Horton模型中表示入渗率衰减的经验系数,多数研究在应用Horton模型时,一般采用土壤自然干燥状态下拟合的β值,未考虑湿润土壤下拟合的折减系数对模型的影响。本研究中干燥条件下Horton模型拟合的折减系数为0.059,湿润条件下拟合的折减系数为0.028,因此,将干燥土壤条件拟合β的Horton模型定义为Horton(0.059)模型,湿润条件下拟合β的Horton模型定义为Horton(0.028)模型,同时在湿润条件下进行比较分析(图2(b))。 图2 不同模型在干燥和湿润条件下对入渗率随入渗历时变化过程的拟合结果与实测值比较 图2(a)为干燥条件的拟合结果,Horton模型拟合的折减系数β值为0.059,拟合曲线的相关指数R2为0.80,Green-Ampt模型拟合得出湿润峰平均水吸力Sf为30 cm,土壤饱和导水率Ks为0.03 cm/min,土壤含水率变化量Δθ为0.2,系数b为0.5,拟合曲线的相关指数R2为0.86。图2(b)为湿润条件下的拟合结果,湿润条件下Horton模型拟合的折减系数β值为0.028,拟合曲线的相关指数R2为0.70,而使用干燥条件下拟合的β值时,Horton模型拟合曲线的相关指数R2为0.66。湿润条件下的Green-Ampt模型沿用干燥条件下拟合的湿润峰平均水吸力Sf,饱和入渗系数Ks等参数值,仅重新拟合相同湿润前期条件下土壤水分变化率Δθ,结果为0.12,拟合曲线的相关指数R2为0.59。总体上看,Horton模型和Green-Ampt模型的入渗率拟合曲线总体趋势接近,在湿润条件下,Horton(0.028)模型拟合曲线整体位于Horton(0.059)模型拟合曲线之上(图2(b)),折减系数β的减小使模型的入渗率模拟结果整体变大。考虑到实际中入渗过程可能受到多因素的综合影响,以上拟合结果可用于分析后续不同入渗模型对LID措施蓄渗性能的影响。 通过对比3种入渗模型在不同前期条件下的入渗率、溢流发生时间和滞蓄总量,分析并讨论不同入渗模型对LID措施滞蓄效果模拟的差异。湿润条件下,考虑不同土壤含水率拟合的折减系数β对Horton模型的影响,对湿润条件下β值的Horton(0.059)模型与干燥条件下β值的Horton(0.028)模型的模拟结果分别进行分析。LID措施的表层蓄水深度取10 cm;汇流面积比取10 ∶1;考虑到城市中多为不透水硬化面,径流系数取0.9。 3.2.1 入渗率 通过计算各入渗模型入渗率模拟值与实测值的平均绝对误差、平均相对误差及相关指数,分析不同入渗模型对LID措施入渗率的模拟精度。各入渗模型在干燥和湿润条件下对入渗率模拟值的误差及拟合相关指数如表2所示。 表2 各入渗模型在干燥和湿润条件下对入渗率模拟值的误差及拟合相关指数 由表2可看出,干燥条件下,Green-Ampt模型的相关评价参数优于Horton模型,Green-Ampt模型入渗率模拟值的平均相对误差比Horton模型小20.1%,平均绝对误差比Horton模型小0.007 cm/min;湿润条件下,Green-Ampt模入渗率模拟值型的平均相对误差及平均绝对误差相对于湿润条件下β值的Horton(0.059)模型仍然更小,Horton(0.059)模型相较于Green-Ampt模型,入渗率模拟值的平均相对误差大3.0%,平均绝对误差大0.001 cm/min。湿润条件下β值的Horton(0.028)模型的各项拟合指标相对Horton(0.059)模型和Green-Ampt模型均更优。相较于干燥条件,湿润条件下Green-Ampt模型的误差略有扩大,平均相对误差增大了5.0%,平均绝对误差增大了0.005 cm/min。湿润条件下的两种Horton模型比干燥条件的误差均有减小,相较于干燥条件,Horton(0.059)模型平均相对误差减小了12.1%,平均绝对误差减小了0.001 cm/min;Horton(0.028)模型平均相对误差减小了19.1%,平均绝对误差减小了0.007 cm/min。 通过上述比较可知,Green-Ampt模型在干燥条件下相较于Horton模型误差更小,而湿润条件下Horton(0.028)模型的精度略高。相比干燥条件,湿润条件下Green-Ampt模型的计算误差明显增大,而Horton模型的计算误差均有所减小。 3.2.2 溢流发生时间 当LID措施表层深度蓄满时,雨水径流继续入流会发生溢流。图3展示了干燥和湿润条件下,不同入渗模型计算LID措施的溢流发生时间随雨强的变化情况,其中,图3(b)中对在湿润条件下区分干燥条件下β值的Horton(0.059)模型和湿润条件下β值的Horton(0.028)模型分别进行分析。 图3 不同模型在干燥和湿润条件下对溢流发生时间随雨强变化过程的计算结果 由图3可看出,无论在干燥还是湿润条件下,在降雨强度较小时,不同入渗模型计算的溢流发生时间差别明显,随着降雨强度的增大,不同模型计算的溢流发生时间差值变小;当降雨强度增大至0.13 cm/min以上时,不同土壤前期条件下、不同模型计算的溢流发生时间绝对差值很小,均小于1.0 min。 各入渗模型计算的溢流发生时间的差别与降雨强度有关。在图3(a)所示干燥条件下,降雨强度分别为0.01、0.07和0.13 cm/min时,3种模型计算的溢流发生时间的最大差值分别为93.76、3.59和1.15 min。在图3(b)所示湿润条件下,降雨强度分别为0.01、0.07和0.13 cm/min时,包括Horton(0.028)模型在内的4种模型计算的溢流发生时间的最大差值分别为118.94、2.18和0.73 min;不包括Horton(0.028)模型时,其他3种模型计算的溢流发生时间的最大差别分别为80.67、1.68和0.73 min。可见,3种模型计算的溢流发生时间的差值随降雨强度的增大逐渐减小,但Horton(0.028)模型在降雨强度较小时与其他模型差别较大,相比于不考虑Horton(0.028)模型的情况,在降雨强度为0.01 cm/min时,模型间差值扩大了47.4%,该差值随降雨强度的增大而减小,在降雨强度大于0.13 cm/min时,各模型间的差值没有扩大。 各入渗模型计算的溢流时间的差值也与土壤的干湿条件有关。当降雨强度为0.01 cm/min时,在考虑Horton(0.028)模型的情况下,湿润条件下各模型计算的溢流发生时间的最大差值相较于干燥条件下增大了27%,在不考虑Horton(0.028)模型的情况下,最大差值相比干燥条件下减小了14.0%;降雨强度为0.07和0.13 cm/min时,湿润条件下各模型计算的溢流发生时间的最大差值相较于干燥条件下分别减小了39.0%和37.0%。可见,降雨强度较小时,Horton(0.028)模型计算的溢流时间相比其他模型更长,而导致了差值扩大,但这种差值扩大会随着降雨强度的增大而消失。因此,3种模型之间计算的溢流时间差值会随着降雨强度的增大和土壤前期含水率的提高而减小,但差异主要受降雨强度的影响。 3.2.3 滞蓄总量 当溢流发生时,LID措施处于积水入渗状态,此时,LID措施的滞蓄效果仅与其自身入渗能力有关。LID措施发生溢流时的滞蓄总量等于其累计入渗量与LID措施表层蓄水量之和。各入渗模型在干燥和湿润条件下计算的不同降雨历时滞蓄总量如图4所示。为区分不同土壤含水状况,图4中降雨历时分别选取30、60和120 min。图4(b)中对湿润条件下区分干燥条件下β值的Horton(0.059)模型和湿润条件下β值的Horton(0.028)模型分别进行分析。 图4 各入渗模型在干燥和湿润条件下计算的不同降雨历时滞蓄总量 由图4可看出,各模型计算的滞蓄总量的相对大小受土壤含水率和降雨历时的影响。在干燥条件下(图4(a)),稳定入渗模型计算的滞蓄总量始终最小,Green-Ampt模型计算的滞蓄总量在短历时情况下大于Horton模型,随降雨历时的增长,Horton模型计算的滞蓄总量逐渐超过Green-Ampt模型的计算值。如降雨历时为30 min时,Green-Ampt模型计算的滞蓄总量比Horton模型的计算值高2.4%,而降雨历时为120 min时,比Horton模型的计算值小0.5%。在湿润条件下(图4(b)),Horton(0.028)模型计算的120 min降雨历时的滞蓄总量达19.45 cm·m2,大于干燥条件下所有模型的滞蓄总量计算值,反映了Horton(0.028)模型的计算入渗率较大,使得计算的滞蓄总量也较大。Green-Ampt模型计算的滞蓄总量在降雨历时为30 min时,比Horton(0.059)模型大5.4%,比Horton(0.028)模型大0.5%,而降雨历时达到120 min时,比Horton(0.059)模型小2.8%,比Horton(0.028)模型小13.1%。随着降雨历时的增长,Green-Ampt模型计算滞蓄总量逐渐小于Horton模型,且随着土壤前期含水率的提高,这种趋势更加明显。 在干燥条件下(图4(a)),降雨历时为30、60、120 min时,3种模型计算的滞蓄总量最大差值分别为3.1、3.6、3.4 cm·m2;在湿润条件下(图4(b)),降雨历时为30、60、120 min时,不考虑Horton(0.028)的3种模型计算的滞蓄总量最大差值分别是2.1、2.1、1.7 cm·m2,相比干燥条件下分别减小了32.3%,41.7%,50.0%,考虑Horton(0.028)模型时,3种模型计算的滞蓄总量最大差值分别为2.1、2.9、3.4 cm·m2,相比干燥条件下分别减小了32.3%、19.4%、0。由此可见,Horton(0.028)模型计算滞蓄总量与其他模型计算值的差值随降雨历时的增长而增大,降雨历时为30、60、120 min时,相比不考虑Horton(0.028)模型时,模型差值分别增大了0、38%、50%,不考虑Horton(0.028)模型时,3种模型计算结果的差值随降雨历时的增长和土壤前期含水率的增大而稳定减小。 入渗率、溢流发生时间和滞蓄总量模拟结果的差别反映了不同模型各自的特点。从入渗率模拟角度来看,稳定入渗模型取入渗稳定时的入渗率,不受土壤含水率变化的影响,模拟精度最低;Green-Ampt模型的入渗率模拟精度在干燥条件下较高,湿润条件下仍然优于干燥条件下β值的Horton(0.059)模型;湿润条件下β值的Horton(0.028)模型的入渗率模拟精度在湿润条件下最高,但在模拟小雨强下的溢流时间和长历时下的滞蓄总量时与其他模型差异较大。相对于干燥条件,湿润条件下Green-Ampt模型的入渗率模拟精度随土壤含水率的增大而降低,Horton模型的入渗率模拟精度随土壤含水率的增大而提高。从溢流发生时间角度来看,降雨强度的增大和前期土壤含水率的提高均会减小不同模型模拟值之间的差别,且该差别主要受降雨强度影响。湿润条件下,Horton(0.028)模型在雨强较小时与其他模型差别较大,在雨强为0.01 cm/min时,Horton(0.028)模型使各模型模拟值的差值增大了47.4%,差值随降雨强度的增大而减小。当雨强增大至0.013 cm/min以上时,干燥条件下,3种模型计算的溢流时间的差值小于1.2 min;湿润条件下,3种模型计算的溢流时间的差值小于0.8 min。从滞蓄总量角度来看,稳定入渗模型的计算滞蓄总量在不同条件下均为最小,Horton模型与Green-Ampt模型的计算滞蓄总量相对接近,Green-Ampt模型的计算滞蓄总量随降雨历时增长的增长率相对Horton模型更小,这表明土壤前期含水率对Green-Ampt模型计算的滞蓄总量影响更大。不考虑Horton(0.028)模型时,其他各模型计算的滞蓄总量差值随降雨强度和土壤前期含水率的增大而逐渐减小;Horton(0.028)模型计算值与其他模型计算值的差值随降雨历时的增大而增大,当降雨历时为120 min时,相比不考虑Horton(0.028)模型时的各模型计算值的差值增大50.0%。 稳定入渗模型不受土壤前期条件的影响,随着雨强增大、降雨历时增长、土壤含水率上升,稳定入渗模型计算结果与其他模型之间的差值会逐渐缩小,能基本满足对LID措施滞蓄效果的保守计算。折减系数β对Horton模型的计算值影响非常大,土壤湿润条件下的β拟合值受实测数据波动的影响,会导致β取值较小,整体入渗率较高,从而使计算的溢流时间和滞蓄总量较大。Green-Ampt模型拟合参数多,计算相对复杂,入渗率拟合时误差较小,对滞蓄总量的计算受土壤含水率变化影响较大,但总体精度优势相对Horton模型并不明显。本文对现有入渗模型的对比与评价是在简化整个降雨过程后进行的,未来的研究方向是优化模型,针对不同雨型的降雨事件,比较不同入渗模型模拟的LID措施在滞蓄总量、洪峰削减量、洪峰来临时间上的差别,更进一步地探索不同入渗模型对LID措施滞蓄效果计算的精度和适用性。 本文对比了稳定入渗模型、Horton入渗模型和Green-Ampt入渗模型计算LID措施滞蓄能力的差异,结果表明,稳定入渗模型应用便捷,但仅能满足对LID措施滞蓄效果的保守计算;Horton模型的折减系数β率定受土壤含水率的影响较大,β在湿润条件下拟合值更小,导致各项计算结果相对其他模型更大;Green-Ampt模型参数较多,应用较复杂,但入渗率模拟精度相对较高,对溢流发生时间和滞蓄总量的模拟结果与干燥条件下拟合的Horton模型接近。具体结论如下: (1)对于入渗率的模拟,稳定入渗模型的精度最低,Green-Ampt模型精度略高于Horton模型,随着土壤含水率的增大,Green-Ampt模型相对误差也增大,而Horton模型相对误差减小。干燥条件下,Green-Ampt模型相比Horton模型相对误差小20.1%;湿润条件下,Green-Ampt模型相比Horton(0.059)模型相对误差小3.0%,比Horton(0.028)模型相对误差大4.0%。 (2)对于溢流发生时间的模拟,稳定入渗、Horton(0.059)和Green-Ampt 3种模型的计算值差值随降雨强度的增加和前期土壤含水率的增大而缩小。当平均雨强大于0.13 cm/min时,各模型计算的平均溢流时间的差值小于1 min,湿润条件下的Horton(0.028)模型与其他模型差别较大。 (3)对于滞蓄总量的模拟,稳定入渗模型计算结果相对较小。Green-Ampt模型与干燥条件下拟合的Horton模型计算结果接近,相对差值始终在5.4%以内,而与湿润条件下拟合的Horton(0.028)模型差别较大。Horton(0.028)模型计算的滞蓄总量在长历时降雨下明显大于其他模型。
2.2 模型评价参数
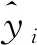
3 结果与分析
3.1 模型参数拟合
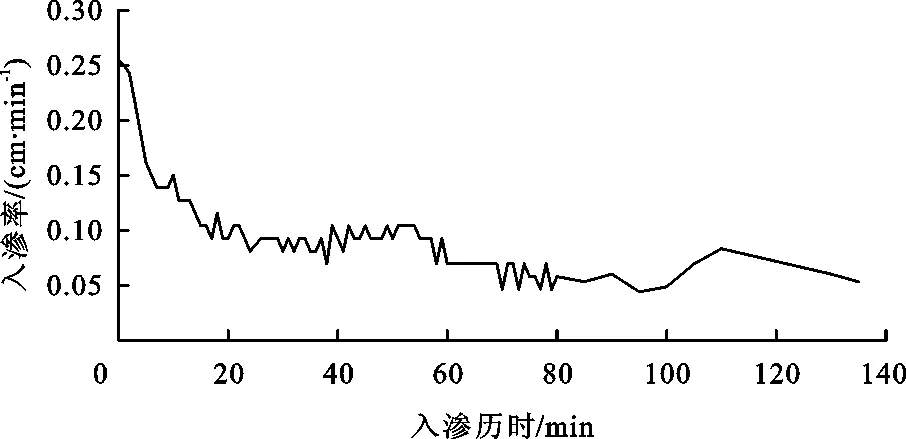
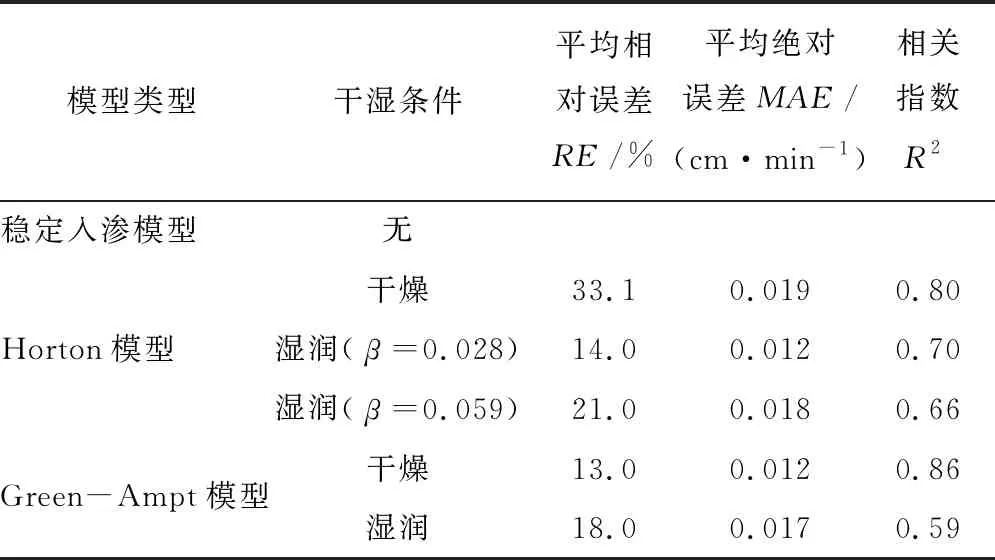
3.2 不同入渗模型对LID措施滞蓄效果模拟的差异

4 结 论

