长距离曲线顶管隧道施工过程中力学行为特征

蒋凯，黄林冲，梁禹

(中山大学航空航天学院，广东深圳 518107)

近年来，随着我国各大城市建设的快速发展，顶管技术正呈现由小孔径浅埋隧道向大直径深埋隧道发展的趋势[1]。目前，国内针对曲线顶管隧道顶推力变化规律及相关力学规律分布研究较少。国内外学者就隧道施工力学特性做了大量相关研究。林越翔等[2]基于多尺度混合建模技术和非线性接触理论，建立了考虑管片接头细部构造和静动应力累积的盾构隧道精细化数值计算模型，研究了盾构正交下穿施工扰动下既有隧道管片结构(含接头)的静动力力学特性。曾勤[3]在普氏压力拱理论及土柱理论下分析了作用于矩形顶管上的管土接触压力、侧摩阻力、掌子面压力等，并给出了不同埋深情况下矩形顶管隧道顶力计算公式。MILLIGAN 等[4-5]对管道所受顶力、顶进轨迹、管壁与土体间接触应力等进行了测试，并分析了轴向偏移与时间对顶管施工过程的影响。马龙飞等[6]对国外顶力计算方法进行汇总并总结，指出了不同计算方法的适用条件及其局限性。叶艺超等[7]根据弹性力学半无限空间柱形圆孔扩展理论和黏性流体力学平板模型理论，假定顶管隧道施工时管节表面与土体之间接触为“固—液”接触，在考虑泥浆触变性基础上推导了一种新的顶管顶力计算公式。HUANG 等[8]通过现场监测和数值模拟，对天津地铁1 号线盾构隧道衬砌破坏进行了实例研究，研究了管片衬砌损伤机理和稳定效果。丁传松[9]在普氏土压力拱理论下推导了直线顶进时顶管顶推力计算公式，并将实际工程中所测顶推力与顶力计算拟合值做了对比，验证了其合理性。梁禹等[10]对管片衬砌在施工期和后期所受外荷载和结构内力进行长期现场追踪测试，总结了衬砌结构外荷载和内力随时间的变化规律。由上述研究总结可知，我国关于直线隧道方面的研究较为常见，由于曲线顶管隧道的特殊性和施工设计的复杂性，近年来针对曲线顶管受力分析及理论模型甚少。本文以广州市南沙区口岸站-凫洲站电力管廊工程为例，对曲线顶管顶进过程中顶力数据进行现场实测，对其受力特征展开分析，并结合顶管施工技术及验收规范[11]进行理论计算，进一步揭示了顶管施工过程中力学行为特征及变化规律。

1 工程实测

1.1 基本工程实测

口岸站—凫洲站110/220 kV 电力管廊口岸段2号～3 号管段位于广州市南沙区，隧道全长195.2 m，其中曲线段131.4 m。顶管内径3 m，外径3.6 m，管节长2.5 m，覆土深度范围位于6～8 m，平面曲率半径600 m，采用泥水平衡式顶管施工。

该段隧道穿越淤泥质土，上覆素填土，下部土层为粉质黏土，施工断面图如图1所示。

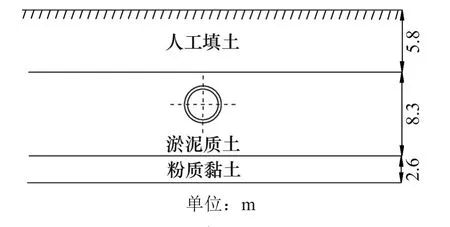
图1 顶管施工断面图Fig.1 Section of pipe jacking construction

由详勘数据可知，顶管机穿越淤泥质土地层，该隧道上覆土体大部分为人工填土，土体坚实系数fkp=0.8，平均覆土深度7.5 m。固结快剪指标：c=9.0 kPa，φ=20°。隧道的管节设计参数如表1所示。

表1 管节设计参数Table 1 Pipe section design parameters

1.2 顶管隧道施工状况

本次顶进距离全长为195.2 m，顶进过程中对顶力数据进行记录，如图2所示。

图2 顶推力随顶进距离变化关系Fig.2 Relation of jacking force change with jacking distance

由实测数据可知，随顶进里程增加，顶推力稳步增长，可看出明显线性对应关系，拟合优度R2=0.846 4。随着隧道推进，泥浆套形成良好，减阻效果明显，顶力最终稳定在6 330 kN左右。

2 曲线顶管隧道管壁摩阻力计算方法

由于隧道埋深恰好位于2～3 倍顶管隧道直径范围内，目前对于这一埋深范围内土压力计算公式尚无明确定义。本文基于普氏压力拱理论及土压力理论公式，得出适用于该实际工况的管壁摩阻力计算公式。

2.1 普氏压力拱理论下土压力及侧摩阻力

通过深埋隧道计算模型，得出普氏压力拱理论下土压力示意图如图3所示。

图3 普氏压力拱理论下土压力计算简图Fig.3 Calculation diagram of earth pressure under the Theory of Platt’s collapse arch

普氏理论下顶管隧道覆土深度由下式得出[10]：

由普氏压力拱理论可知，洞室开挖后顶部岩体塌落成一抛物线状的天然拱。

由于隧道截面的对称性，故可取隧道1/4 圆弧进行受力分析，如图3所示。

设作用在ds上的竖向正压力为dNv，则有：dNv=qv1sinθds， 作用在ds上的正压力dN=dNvsinθ=qv1sin2θds。

经过积分得右上角圆弧段竖向正压力为：

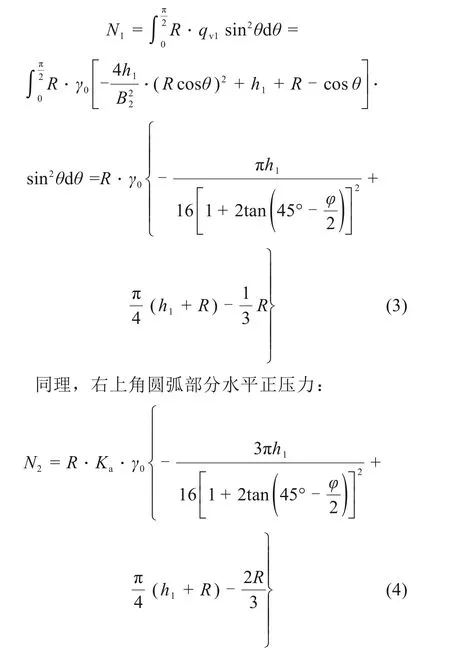
式中：Ka为主动土压力系数；qv1=γ0(H+R-Rsinθ)；γ0为土体平均重度。

2.2 土柱理论下土压力及侧摩阻力分析

通过建立浅埋隧道计算模型，可得土柱理论下的土压力计算简图如图4所示。

图4 土柱理论下土压力计算简图Fig.4 Schematic diagram of soil pressure under soil pillar theory

通过积分得到右上角圆弧竖向土压力：

其中：ω为管节单位长度自重，kN/m。

根据实际工况，不考虑顶进时本案例中淤泥质土中顶管与土层间摩擦因数可取0.2[11]。调研相关文献[12-14]发现，当管土摩擦为流体摩擦(含润滑剂)时，摩擦因数取值范围为0.1～0.3，且顶管施工时注浆作用可使阻力减少30%～50%。考虑注浆影响，本案例中取50%，即顶管隧道顶进时摩擦因数f取值为0.1。

3 曲线顶管隧道顶力计算方法

为得出适用于本实际工况的侧摩阻力公式，本文拟推导曲线顶管隧道顶进过程中基坑底座处总顶力与管侧摩阻力、端面阻力关系式，并将上述普氏理论与土柱理论下计算所得侧摩阻力公式代入所得表达式。

设管侧摩阻力为Ff，始发井对应为第1 节管节，顶进最前端管节为第n节，第n节管节所受顶推力为Fn，第1管节所受顶推力为F1，示意图如图5所示。

图5 曲线顶管顶进示意图Fig.5 Schematic diagram of curve pipe jacking

取初始段管节进行受力分析，其受力示意如图6所示。

图6 初始段顶管受力分析示意图Fig.6 Schematic diagram of force analysis of pipe jacking in initial section

由图3可得顶力关系表达式：

由此可推导出F1与Fn关系式：

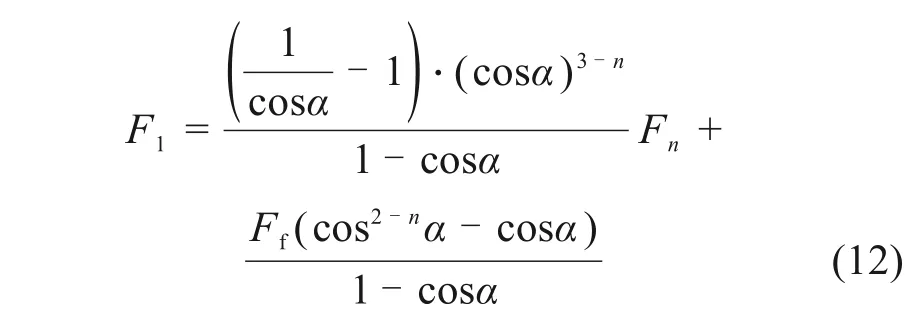
参考相关文献[15-16]，对第n节管节受力分析有：

其中：F端为第n节管节所受端面阻力。

由于地下水位位于隧道以下，故不考虑地下水位影响。设第n节管节所受端面阻力F端，查阅已知文献[17]可知，顶管端面阻力可计算为：

式中：D为顶管隧道外径，m；H为管顶埋深，m；γ0为土体平均重度；Ka为主动土压力系数；Ap为顶管机机头横截面积。

结合式(12)～(14)，可得顶推力与弯曲角和侧摩阻力之间的表达式：

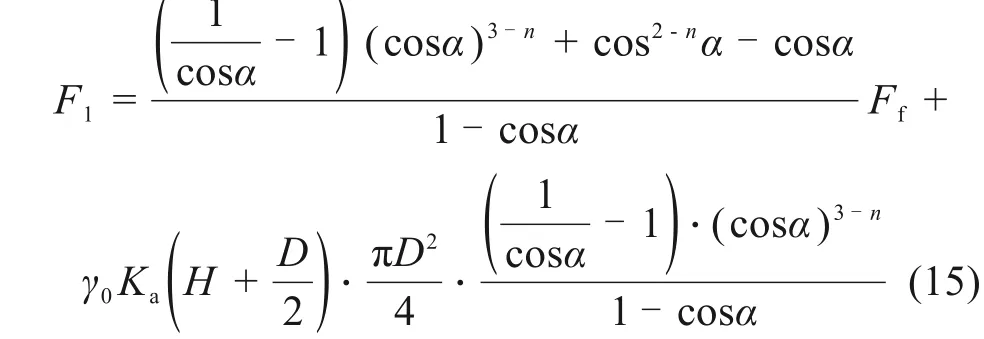
以南沙口岸段2 号～3 号曲线顶管隧道为例进行验证分析，普氏土压力理论与土柱理论所得管侧摩阻力分别为90.03 kN，120.14 kN。定义初始段管节顶进土体时实测顶推力为初始顶推力Fp，实测总顶推力F0，2 种土压力理论下初始顶推力、总顶推力与实测数据误差对比如表2所示。

表2 不同土压力理论下初始顶推力、总顶推力与实测数据对比Table 2 Table of comparison of initial thrust,total thrust and measured data under different soil pressure theorie

采用浅埋土柱理论与普氏土压力理论计算所得顶管初始顶推力与实测数据误差较大，计算所得初始顶推力偏于保守，约为实测初始顶推力的1/2。分析原因后发现分析计算时未考虑顶管机机头影响。由于顶管隧道开始顶进时，最大静摩擦因数大于动摩擦因数，且本文计算中默认管节为混凝土段管节，未考虑顶管机机头段重量影响，故初始段顶推力理论计算值偏小。将2种土压力理论下侧摩阻力代入本文推导所得顶推力公式，结果表明普氏理论下所得总顶推力与实测数据误差为23.40%。土柱理论下总顶推力与实测总顶推力误差为103.06%，误差较大，不予考虑。故这里采用普氏土压力理论计算所得侧摩阻力进行计算，计算用具体参数如表3所示。

表3 覆土参数及管节数Table 3 Soil parameters and pipe joint number

3.1 管缝张开角变化对顶推力影响

根据已有文献[9]研究结果，顶管隧道管缝张开角一般小于2°，故将此值设为最大管缝张开角。为研究曲线顶管隧道顶推力与管缝张开角变化特征，将与该工程案例相同长度的曲线隧道进行理论推导。将上述土体参数代入式(15)，绘制该案例中顶推力随管缝张开角变化曲线如图7所示。

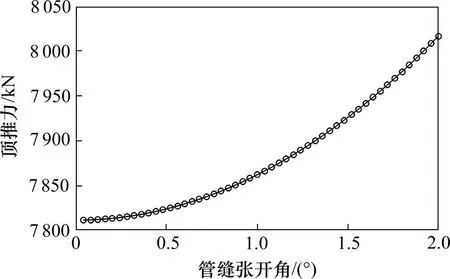
图7 顶推力随管缝张开角变化曲线Fig.7 Jacking force varies with the opening angle of the pipe joint

由图7可看出，顶推力随管缝张开角增加而增大，且增长速率逐渐加快；当管缝张开角位于0.25°以下时，顶推力变化可忽略不计，说明轻微的管缝张开角对顶推力变化影响有限。该算例中曲率半径为600 m，由图5 计算可得对应管缝张开角为0.24°，此时管缝张开角对顶力影响较小，该研究结论可为曲线顶管隧道顶推力设计值及中继间增压泵型号选取等提供借鉴意义。

3.2 曲线顶管隧道曲率变化对顶推力影响

由图5 所示曲线顶管顶进示意图，可得几何关系。

将式(16)代入式(15)中，绘制顶推力随曲率K变化曲线如图8所示。

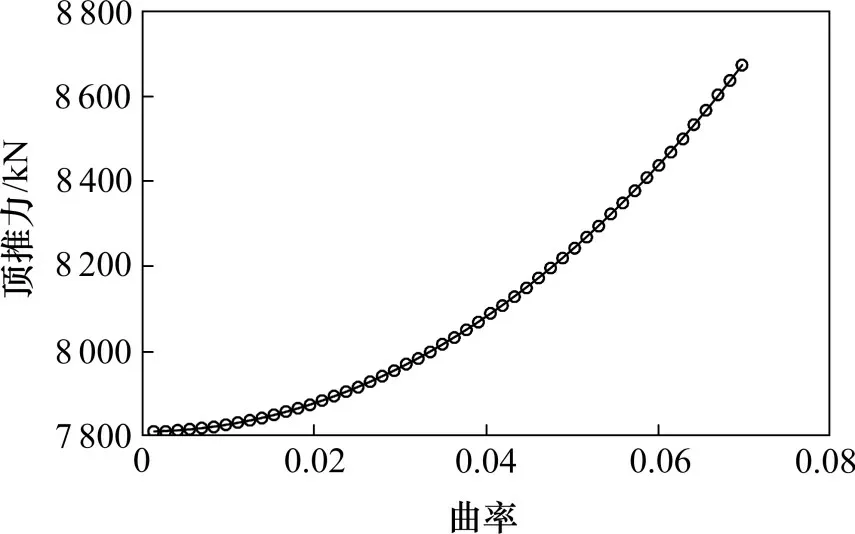
图8 顶推力随顶管曲率变化曲线Fig.8 Thrust varies with the curvature of the pipe

如图8 所示，K=0.01 时，对应顶推力7 827.1 kN，与直线段顶进(K=0)时顶推力相差仅为0.2%。由该对比结果可知，当曲率小于0.01，即曲率半径大于100 m，顶推力变化趋势不明显，计算顶推力时可近似看作直线顶进。当曲率超过0.01，即曲率半径小于100 m 时，顶推力受曲率影响不可忽略，总体上顶推力随曲率增加而增大，且增长速率逐渐加快，该研究结论可为曲线顶管顶推力控制提供有效参考。

3.3 顶管顶推力随顶进距离变化关系

该实际案例中顶管隧道曲率半径为600 m，对应曲率小于0.01，由图8 可知，此时顶推力随曲率变化趋势不明显，故可在顶推力计算时将口岸段2号～3 号隧道全程近似为大曲率曲线隧道计算。绘制预测顶推力与实测顶推力随顶进距离变化曲线图如图9所示。

由图9可知，本文推导所得预测顶推力随顶进距离近似表现为线性关系，对比实测顶推力随顶进距离变化曲线后发现变化规律基本相同。为衡量其拟合程度，现采取回归评价指标拟合优度进行验算。拟合优度R2(Goodness of Fit)可表示预测值对真实值的拟合程度，定义其表达式：其中：yi-y＾i为真实值-预测值；yˉi为样本平均值；m为样本总数。代入实测顶力数据及预测值，可得拟合优度R2=0.85。结果表明实测顶力数据及预测值拟合度较好，验证了本文推导公式的合理性。计算所得顶推力与实测数据顶进中间段部分略有不同，中间段理论值整体偏小，经实地勘测后发现顶管下穿土体中含有大量止水带和塑料排水板，隧道顶进受阻，推测该为实测顶推力偏大主要原因。由于实际工况的复杂性，本文中简化计算模型未能完美模拟实际工况，但揭示了实际变化规律，具有一定参考意义。

图9 预测顶管顶推力与实测顶推力随顶进距离变化对比Fig.9 Comparison diagram of predicted jacking thrust and measured jacking thrust varying with jacking distance

4 结论

1) 顶管施工初期，随顶进里程增加，顶推力稳步增长，可看出明显线性对应关系。管壁注浆后减阻效果明显，顶力降低，管道在良好泥浆套顶进时，顶力最终稳定在一定范围内。

2) 顶推力随管缝张开角增加而增大，且增长速率逐渐加快；当管缝张开角位于0.25°以下时，顶推力变化可忽略不计，说明轻微的管缝张开角对顶推力变化影响有限。

3) 当曲率小于0.01 时，顶推力变化趋势不明显，之后增长速率逐渐加快，具体表现为初期上升变化缓慢后期增长速率加快。

4) 本文推导所得顶推力与顶进距离关系近似表现为线性。预测顶力与实测数据拟合较好，拟合优度R2=0.85。理论解偏于保守，但能较好地预测顶力变化，验证了本文推导公式的合理性。