基于改进修正权重的证据组合方法

蒋 斌，梁小安，张 亮，高杨军

空军工程大学 装备管理与无人机工程学院，西安710051

D-S证据理论[1-2]具备坚实的数学理论基础，相较于传统概率论能够更好地进行不确定信息的表达、处理和融合，因此自提出以来就逐步在信息融合[3-4]、风险评估[5]、模式识别[6-7]、决策分析[8-9]等诸多领域得到了广泛应用。同时，针对D-S证据理论在处理高冲突证据时出现的悖论问题[10-11]，众多学者进行了针对性研究[12-15]，其中，修正证据源的解决方法保留了经典Dempster组合规则满足交换律、结合律等性质的优良特性，更有利于降低证据理论在工程应用中的计算复杂度。为此，本文从修正证据源的思路出发，以修正权重的确定为研究重点，通过对证据源的预处理提出证据信息有效组合的科学方法。

针对证据修正权重的确定问题，Murphy[16]提出的证据算术平均组合方法对每条证据赋予了相同的权重，在解决证据冲突的同时却忽视了证据间的关联关系。我国学者邓勇[17]引入Jousselme距离衡量证据间的冲突程度，进而通过对证据关联关系的有效量化确定了修正权重，为此类问题的解决提供了全新思路。随后，文献[18]和文献[19]则分别利用Pignistic概率距离和兰氏距离对证据冲突进行了度量，提出了相应的修正权重确定方法；文献[20]将证据看作向量，基于向量相似度对冲突证据进行了修正组合，克服了传统冲突度量方法存在的不足；文献[21]在利用Pignistic概率函数对非单子集进行转换的基础上，引入了相关系数，实现了相关系数在证据修正权重确定中的有效应用；文献[22]则通过对相关阈值的设定比较，给出了局部冲突修正和全局冲突分配的不同策略，进一步丰富了冲突证据修正的方法。上述研究成果基于证据冲突程度的不同计算方法对证据修正权重的确定进行了有益的探索，在实际应用中改进了冲突证据组合的收敛性，但这一类方法仅仅关注证据间的关联关系，没有考虑证据综合不确定度对修正权重的影响，弱化了待组合证据的信息价值，导致修正权重的确定存在一定的片面性，证据组合结果的可信度有待进一步提升。

事实上，关联关系是衡量证据可用与否的关键因素之一，它从证据的外部关系反映了证据间的相似性。而不确定度作为反映证据内部可靠性的重要指标，是衡量证据可用与否的另一个重要因素。基于上述分析，本文在对证据综合不确定度进行系统阐述的基础上，从证据外部的关联关系和内部的不确定度入手，分别提出基于改进冲突度的相似性权重确定方法和基于综合不确定度的可靠性权重确定方法，进而得到一种改进的证据修正权重，应用Dempster组合规则对修正后的加权平均证据进行组合，并通过实例验证分析了所提方法的有效性和合理性。

1 D-S证据理论基础

定义1[23]在辨识框架Θ中，若集函数满足，则称m为Θ上的基本概率分配（Basic Probability Assignment，BPA），也称为mass函数，m()A表示证据对命题A的信任程度。若A⊆Θ且m(A)＞0，则称A为m的焦元，所有焦元的集合称为核。

定义2[23]Dempster组合规则。设m1,m2,…,mn为同一辨识框架Θ上相互独立的mass函数，则对于∀A⊆Θ，满足：

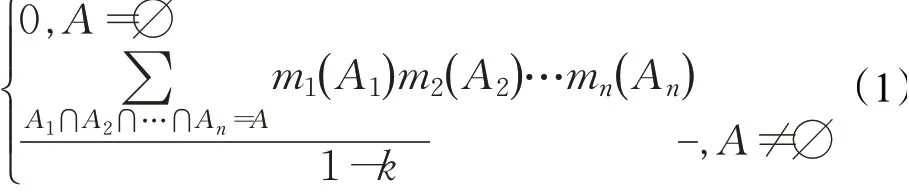
式中，k∈[0],1为冲突系数，表示证据间的冲突程度且

定义3[24]Jousselme距离。设m1和m2是辨识框架Θ上的两个mass函数，则两者之间的Jousselme距离可以表示为：

式中，m1和m2为mass函数的向量形式的相似性矩阵，其元素表示为：

定义4[25]Pignistic概率函数。设m为辨识框架Θ上的mass函数，对于∀A⊆Θ，其Pignistic概率函数为：

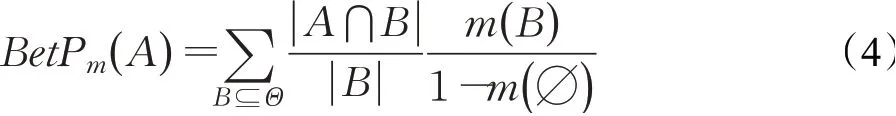
式中，m(∅)≠1，|·|表示子集中所含元素的个数。

2 证据的综合不确定度

证据理论中证据信息的不确定度反映证据的可靠性，对不确定度的有效度量将影响证据组合结果的准确性。文献[26]和文献[27]分别给出Deng熵和证据精度的概念定义，用来衡量证据的不确定度；文献[28]借鉴模糊熵的表达形式，通过对证据体中的命题进行Pignistic概率转换，用求得的熵值表征不确定度的大小；文献[29]对多义度进行了改进，以修正证据向量的Shannon熵实现了对不确定度的度量。证据理论将概率论中的基本事件空间拓展为辨识框架，并在辨识框架上建立了基本概率分配函数，这是其相较于其他不确定性推理方法更能有效表达和处理不确定信息的优势所在，因此，基于对证据体数据结构的分析，提出综合不确定度的科学度量方法。

辨识框架和焦元是证据理论中最基本的数据结构，证据理论通过对不确定信息的分解提炼，将其转化为某一辨识框架下的焦元形式，并赋予一定的基本概率分配，实现对不确定信息的有效表达。因此，证据体中包含了不确定性的多维特性，即随机性和不具体性[30-31]，其中，随机性表现为辨识框架下各焦元的分散性，不具体性表现为焦元内部的不精确性，综合这两个方面能够对证据信息的综合不确定度进行科学完整的度量。

Shannon熵是描述概率理论随机性最好的方式，基于对Shannon熵的认识理解，文献[32]对度量证据体随机性的多种不同形式进行了对比分析，认为式（5）的ST(m)相较于其他形式在绝大多数情况下满足次相加性，能够对随机性进行有效表达。

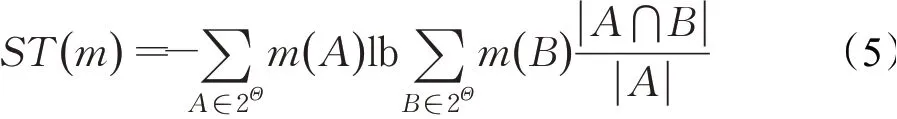
因此，使用ST(m)表示证据信息的随机性，特别地，当证据信息只有一个焦元A且m(A)=1时，ST(m)=0，说明这一信息对于此问题能够给出明确唯一的证据，不具有随机性。

类哈利熵[33-34]是在借鉴哈利熵的基础上提出的，具体表达形式如式（6），因其符合不确定性公式的所有公理性要求，被公认为是表达证据不具体性的理想公式。

当焦元内部的元素越多，其不具体性越大，特别地，当证据体中所有焦元均只有一个元素时，V(m=)0，说明焦元内部没有可选择的元素，在纯粹随机性证据体中没有不具体性。

综上所述，证据体的综合不确定度应由随机性和不具体性两部分组成，随机性用ST(m)确定，表示辨识框架下焦元的分散性，不具体性用V()m确定，表示焦元内部的不精确性，综合两者之和得到式（7），能够较为全面地度量证据的综合不确定度。

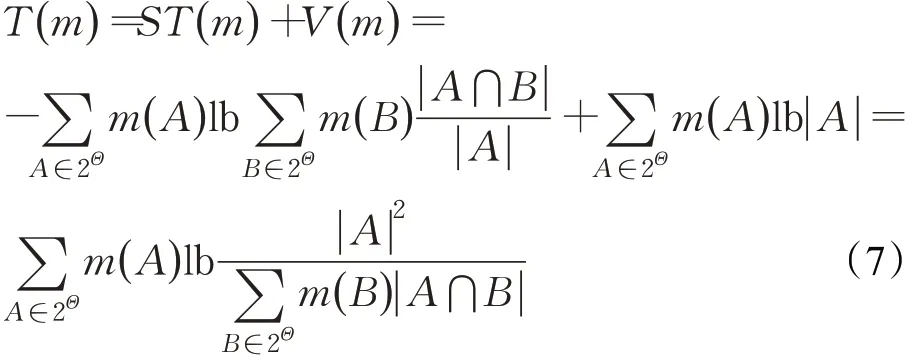
3 改进修正权重的确定方法

从人的认知角度来看，更倾向于选择与其他证据更为相似、证据信息更为可靠的证据作为自身决策判断的依据，因此在确定证据修正权重的过程中，应综合考虑证据间的相似性与证据自身的可靠性两个方面因素。通过对基于改进冲突度的相似性权重和基于综合不确定度的可靠性权重的计算，提出一种改进的证据修正权重确定方法。

3.1 基于改进冲突度的相似性权重确定

冲突系数和Jousselme距离作为衡量证据冲突度的常用指标，在实际应用中还会出现违背常理的情况，但两者存在一定的互补性。因此，基于冲突系数和Jousselme距离确定证据间的改进冲突度，通过改进冲突度得到证据与其他证据的相似性系数，相似性系数越大，则应赋予较大的权重，反之，则应赋予较小的权重。

若θ为Θ中的任一命题，则证据m的最大支持假设为另k12和d12分别表示证据m1和m2之间的冲突系数和Jousselme距离，则证据m1和m2之间改进的冲突度cf12为：

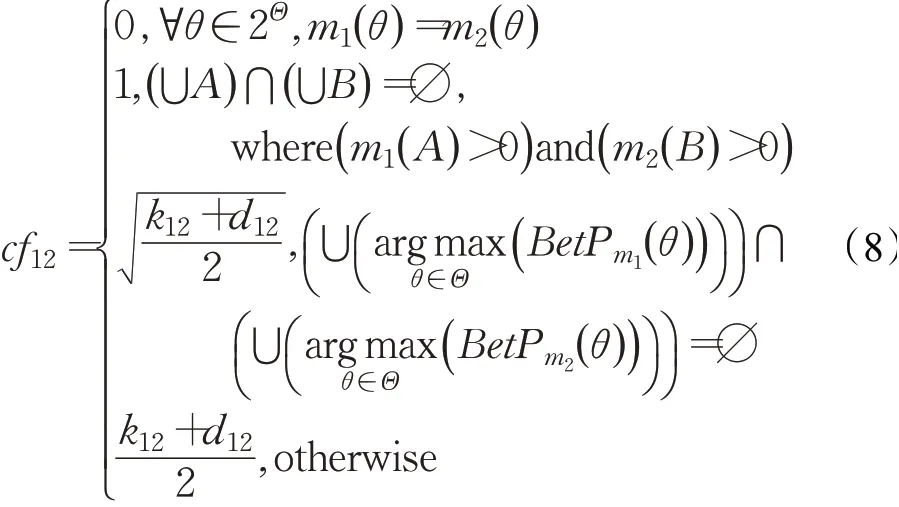
假设有n个待组合证据，则由改进冲突度可计算得到改进冲突度矩阵CF：

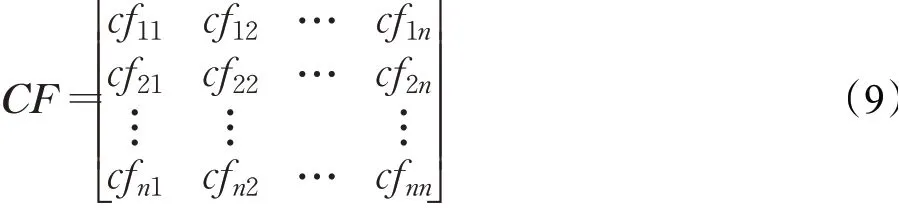
进而计算mi的相似性系数矩阵SM：

从而得到mi的相似性系数S(mi)：

因此，基于改进冲突度的证据相似性权重为：

3.2 基于综合不确定度的可靠性权重确定

基于第2章对综合不确定度的定义，本节提出基于综合不确定度的证据可靠性权重确定方法。证据的综合不确定度越大，其可靠性越低，则应赋予较小的权重，反之，则应赋予较大的权重。

对于证据mi(i=1,2,…,n)，由式（5）和式（6）分别求得证据的随机性ST(mi)和不具体性V(mi)，从而由式（7）得到证据的综合不确定度T(mi)。

因此，基于综合不确定度的证据可靠性权重为：

3.3 改进修正权重的确定

证据之间的相似性和自身的可靠性对于证据组合结果均有较大的影响，只有综合考虑这两个方面才能对证据进行合理的修正。因此，在分别基于改进冲突度确定相似性权重和基于综合不确定度确定可靠性权重的基础上，能够得到改进的证据修正权重为：

式中，η(0≤η≤1)为折衷系数，根据个人偏好确定，若偏好相似性权重，则取0.5＜η≤1；若偏好可靠性权重，则取0≤η＜0.5；若无偏好，则取η=0.5。本文在实例应用中取η=0.5。

4 算例分析

通过改进修正权重对待组合证据进行加权平均后，可以利用Dempster组合规则对证据进行组合，从而得到基于改进修正权重的证据组合完整流程，如图1所示。

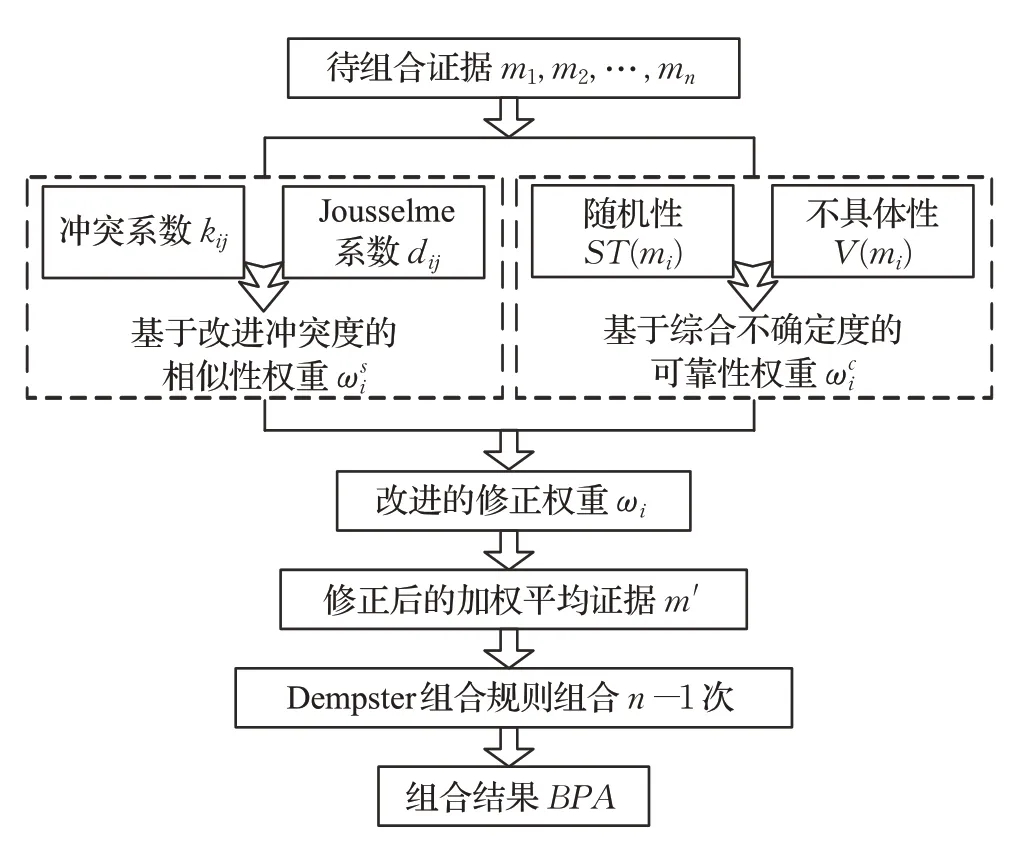
图1 证据组合流程Fig.1 Process of evidence combination

4.1 实例应用

假设识别框架Θ={A,B,C}，有5个证据的基本概率分配函数分别为：

步骤1计算证据相似性权重。由式（2）和式（3）分别计算证据间的冲突系数kij和Jousselme距离dij，进而由式（8）求得改进冲突度cfij(1≤i≤5,1≤j≤5)。这里以cf12为例对计算过程进行说明，由式（2）可得k12=0.709 0，由式（3）可得d12=0.538 6，由式（4）计算m1和m2的Pignistic概率函数为：

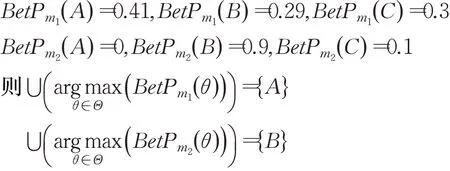
所以

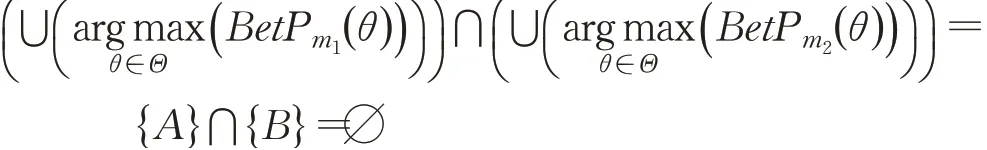
由式（8）可知：

同理，可构建改进冲突度矩阵CF5×5为：

由式（11）得到证据mi(1 ≤i≤5)的相似性系数为：

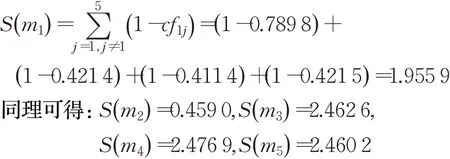
由式（12）得到基于改进冲突度的证据相似性权重为：

当证据组合数量变化时，可得到证据的相似性权重如表1所示。

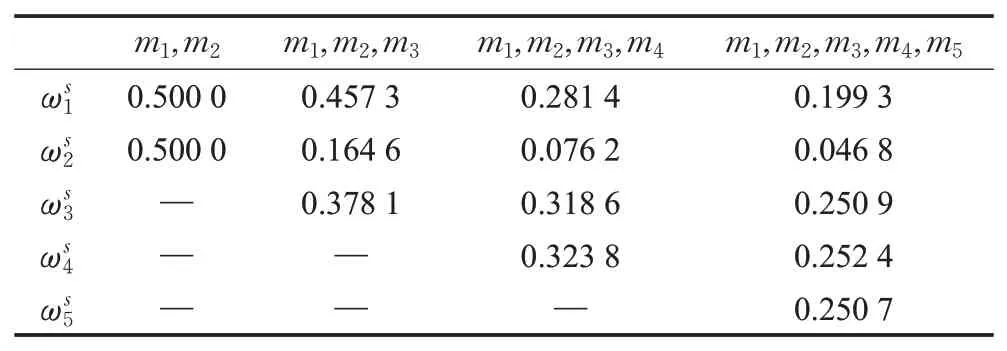
表1 相似性权重Table 1 Similarity weights

步骤2计算证据可靠性权重。由式（5）和式（6）计算证据的随机性ST(mi)和不具体性V(mi)，并由式（7）得到综合不确定度T(mi)，计算结果见表2。

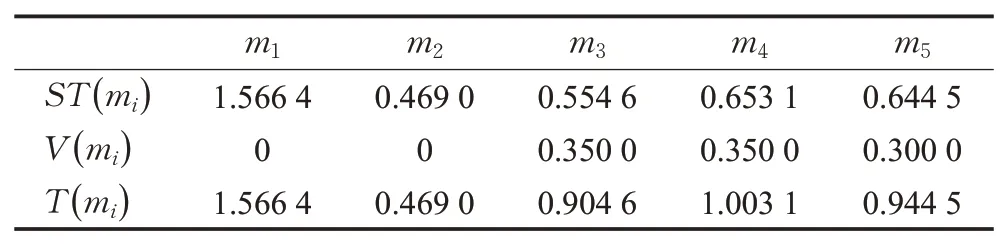
表2 证据不确定度Table 2 Uncertainty degree of evidence

则由式（13）得到证据的可靠性权重如表3所示。

表3 可靠性权重Table 3 Reliability weights

步骤3由式（14）得到改进的修正权重如表4所示。

表4 改进的修正权重Table 4 Improved modified weights

步骤4通过改进的修正权重对原始证据进行修正，得到修正后的加权平均证据m′，如表5所示。

表5 修正后的加权平均证据Table 5 Modified weighted average evidence

步骤5对n个证据进行组合时，应用Dempster组合规则对修正后的证据m′进行n-1次组合，得到组合后最终的BPA如表6所示。

表6 组合后的BPA Table 6 Combined BPA

4.2 对比分析

为验证本文所提方法的有效性和合理性，分别应用Dempster组合方法[1]、Murphy组合方法[16]和Deng组合方法[17]对上例中的证据进行组合计算，各方法的计算结果见表7，同时对组合后的m(A)和m(B)进行对比，如图2和图3所示。

图2 m(A)的组合结果对比Fig.2 Comparison of m(A)’combination result

图3 m(B)的组合结果对比Fig.3 Comparison of m(B)’combination result

表7 不同组合方法的组合结果Table 7 Combination results of different combination methods

通过对组合结果的对比分析可知：

（1）从直观来看，本例中m1、m3、m4、m5认为A的可能性更大，而证据m2则更支持B，因此从证据整体来看，相较于其他证据，证据m2为一条高冲突证据。但由于证据m2中m2(A)=0的存在，使得Dempster组合规

则无法在更多证据支持A的情况下做出合理的决策，始终认为组合后A的值m(A)=0，导致了“一票否决”悖论问题的出现，说明Dempster组合规则无法对冲突证据进行有效组合；而随着证据信息的增加，其他三种方法均能得到合理的组合结果，但Murphy组合方法只是对证据进行了简单的平均，没有考虑证据间的关联关系和自身的可靠性，本文所提方法在综合考虑这两个方面的基础上，在收敛性上相较于Murphy方法也有一定优势。

（2）从图2和图3可以看出，本文所提方法在收敛性上不如Deng组合方法，但结合综合不确定度的计算结果表2就可以给出合理的解释。Deng组合方法在确定修正权重过程中仅仅考虑冲突度，而从综合不确定度的计算结果来看，证据m2的综合不确定度最小，说明m2给出的证据信息更为可靠，因而在对m1、m2或m1、m2、m3进行组合时，赋予了证据m2更高的权重，使得组合结果的m(A)更小，m(B)更大，表明本文所提方法在没有充足证据支持A的情况下，没有一味地追求收敛速度，过早地否定“冲突”证据，而是充分利用了其信息价值。另外，在加入证据m4、m5后，明确了证据m2的冲突性质，从图中可以看出，此时本文方法组合结果的收敛速度更快，说明本文所提方法在证据信息明确可靠的情况下能够更快地得到可信的组合结果。

5 结论

针对证据组合过程中修正权重的确定问题，提出了综合考虑相似性权重和可靠性权重的改进修正权重确定方法。本文的主要贡献和结论如下：

（1）解决了证据不确定度度量不够全面的问题，从随机性和不具体性两个维度给出了证据综合不确定度的计算方法，实现了对证据不确定度的全面度量。

（2）提出了改进修正权重的确定方法，通过基于改进冲突度的相似性权重和基于综合不确定度的可靠性权重确定修正权重，充分考虑了证据间的相似性和自身的可靠性，所得改进的修正权重更加科学合理。

算例分析结果表明，基于本文改进修正权重的证据组合结果更加客观、准确，充分利用了证据信息，证据组合过程更加符合人的客观认识，组合结果可信度更高。