基于正弦因子和量子局部搜索的灰狼优化算法

徐辰华，骆珠光，吴冠宏，刘 斌

1.广西大学 电气工程学院，南宁530004

2.广东技术师范大学 自动化学院，广州510630

灰狼优化算法（Grey Wolf Optimization algorithm，GWO）是由Mirjalili等人[1]在2014年从灰狼阶级层次的特点的启发下提出来的。该算法通过模仿灰狼群体捕食行为来寻找目标问题的最优解。与现有启发式算法相比，GWO操作简单，调整的参数少，且由于它的最优个体及运动方式依概率更新，具有更大的随机性和更快的收敛速度，并在工程实践的初步应用中取得了良好的效果。

灰狼算法在求解一些复杂问题时，表现出了良好的性能，如求解柔性车间调度问题[2]、神经网络的优化[3]、支持向量机的优化[4]等。目前国内外一些学者针对GWO进行了研究，文献[5]为解决复杂的高维函数问题，将混沌理论和精英反向学习策略引入灰狼算法。文献[6]提出一种自适应递减的收敛因子和基于惯性权重的步长更新公式改进的灰狼算法，提高了算法的搜索能力。文献[7]对灰狼算法的位置更新，用最优-最差正交反向学习策略来改进，用于优化多核极限学习机中的加权系数等参数。文献[8]提出一种混合灰狼算法，将DE的交叉、变异因子引入算法中，提高了算法的性能。文献[9]在GWO算法的基础上引入Tent映射和正态云模型，分别从狼群初始分布和位置更新策略上改善算法寻优性能。上述改进方法虽然提高了GWO某一方面的性能，但是在算法收敛速度和寻优精度上难以达到很好的平衡。

针对上述的问题，本文提出一种基于正弦控制因子和量子局部搜索的灰狼优化算法（Quantum Gray Wolf Optimization algorithm，QGWO）。首先，将控制因子按照具有正弦变化的曲线变化，使改进的算法在迭代前期加快收敛速度以快速完成全局探索，而在迭代后期减缓收敛速度以提高搜索精度；同时，引入量子局部搜索降低算法陷入局部最优解的概率；最后，通过12个标准测试函数进行实验和工程实例验证，实验结果表明，QGWO算法具有更高的寻优精度和更快的寻优速度，能够有效处理高维复杂问题，可以有效平衡算法的收敛速度和寻优精度。

1 灰狼优化算法

灰狼群体社会等级机制如图1所示。分别为统领狼α、副统领狼β、普通狼δ和底层狼ω。GWO算法主要包括三个环节：包围猎物、追捕猎物和攻击猎物。

图1 灰狼种群等级制度示意图Fig.1 Schematic diagram of grey wolf population hierarchy

1.1 包围猎物

狼群在确定猎物位置后，首先对猎物进行包围，在此过程中灰狼与猎物的距离可表示为：

其中，t是迭代次数，Xp(t)是猎物的位置，X(t)是第t次迭代后灰狼的位置。A和C是矩阵系数，其定义如下：

其中，r1、r2表示[0，1]间的随机变量，a随着迭代次数的增大从2线性递减到0，表达式为：

式中，tmax表示最大迭代次数。

1.2 追捕猎物

对猎物进行围困后，β、δ狼在α狼的带领下对猎物进行追捕，在追捕过程中，狼群个体位置会随着猎物的逃跑而改变，因此灰狼群体可以依据α、β、δ的位置Xα、Xβ、Xδ进行灰狼位置的更新：

其中，X(t+1)表示灰狼在的最终更新位置。

1.3 攻击猎物

攻击是狩猎的最后一步，狼群对猎物进行击杀，即得到最优解。这个过程的完成，主要是通过式（5）中a值的递减来实现，当a的值从2线性递减到0时，则与其对应的A的值也在区间[-a,a]变化。

2 改进的灰狼优化算法

灰狼优化算法在复杂问题的求解上，存在收敛精度不高，收敛速度缓慢，易于陷入局部最优等缺陷[10]。参数a决定了控制参数A的变化，如式（5）所示，A被限制在[0，2]的区间内。当||A≥1时，算法进行全局探索，当|A|＜1时，则算法进行局部搜索，故参数a的变化会影响算法的搜索范围。因此针对上述问题，对灰狼算法进行以下的改进。

2.1 控制因子正弦变化

由上述可知，a越大，算法的全局探索能力越强；a越小，算法的局部搜索能力越强。式（5）描述的参数a是呈线性递减的，为了提高算法的局部搜索能力，所以对式（5）进行改进。本文根据正弦曲线变化的特点，将控制因子a的变化改成式（9），控制因子a的变化趋势由线性递减变成迭代前期减小速度较快，而在迭代后期减小速度变慢。则算法在迭代前期能够快速完成全局搜索，在迭代后期可以充分进行局部搜索。

2.2 引入个体平均历史位置

为了提高算法的性能，对每一只灰狼建立历史最优位置的记录Xhi，以及整个灰狼群体的历史最优位置Xg，设Xm是平均灰狼的历史最好位置。

其中，N为种群个数。

2.3 量子局部搜索

首先计算当前代的自适应扩张系数：

其中，tmax为最大迭代次数，βmax和βmin为预设的自适应扩张系数的最大值和最小值，一般为1和0.5。再根据式（10）计算平均灰狼历史最好位置，基于个体历史最优和群体历史最优位置，生成一个吸引点：

其中，ϕ是一个1×d的在[0，1]之间服从均匀分布的随机数矩阵。

以δ势阱为基础，假设每一个狼群的位置向量具有量子行为，利用波函数ϕ(x,t)来描述该位置向量的状态。假设狼群在以吸引点为中心的一维δ势阱中运动，解一维δ势阱的薛定谔方程（Schrodinger），得到该位置向量在空间某一点出现的概率密度函数：

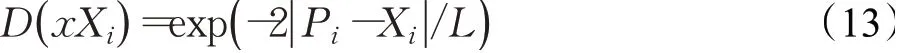
再通过蒙特卡罗（Monte-Carlo）随机模拟得到新的位置向量的位置方程为：

其中，u是一个1×d的在[0，1]之间服从均匀分布的随机数矩阵。

2.4 算法步骤

步骤1初始化算法参数，群体规模大小为N，最大迭代次数tmax，以及初始化群体位置。

步骤2计算每个灰狼个体的适应度值，并记录个体历史最优以及群体历史最优位置，选择适应度值最小的前3个个体位置，分别为Xα、Xβ、Xδ。

步骤3按照式（6）计算剩余个体ω与Xα、Xβ、Xδ的距离，并根据式（6）～（8）更新灰狼α、β、δ和猎物的位置。

步骤4按照式（3）、（4）更新参数A、C的值和式（9）更新参数a的值。

步骤5计算当前代的自适应扩张系数以及平均灰狼历史最好位置Xm。

步骤6基于个体历史最优和群体历史最优位置，生成一个吸引点，并根据公式（10）～（14）进行基于量子行为的位置更新。

步骤7若算法到达最大迭代次数tmax，算法结束并根据式（8）输出最优解Xα；否则，返回步骤2。

3 仿真实验及分析

3.1 测试函数及性能指标

所有仿真实验在Intel®CoreTM，CPU i7-8550U，12 GB内存和Windows 10的PC上运行，程序采用MATLAB 2018a的M脚本语实现。本文选取了12个标准测试函数进行仿真实验，用来验证所提出的QGWO算法的有效性，并将最优解在原点或原点附近的测试函数进行了随机位移。测试函数表达式、自变量的搜索范围和最优值如表1所示。其中，f1～f4是不定维单峰函数，f5～f8是不定维多峰函数，f9～f12是固定维多峰函数。单峰函数主要用于测试算法的收敛速度和求解精度，多峰函数主要用于测试算法全局搜索能力。由于最优解是优化算法的搜索目标，为了更好地评价优化算法的性能，本文用算法对各测试函数的最佳求解结果的均值和标准差来评价各算法的性能。其中，平均值反映算法求解精度，标准差反映了算法求解的稳定性。

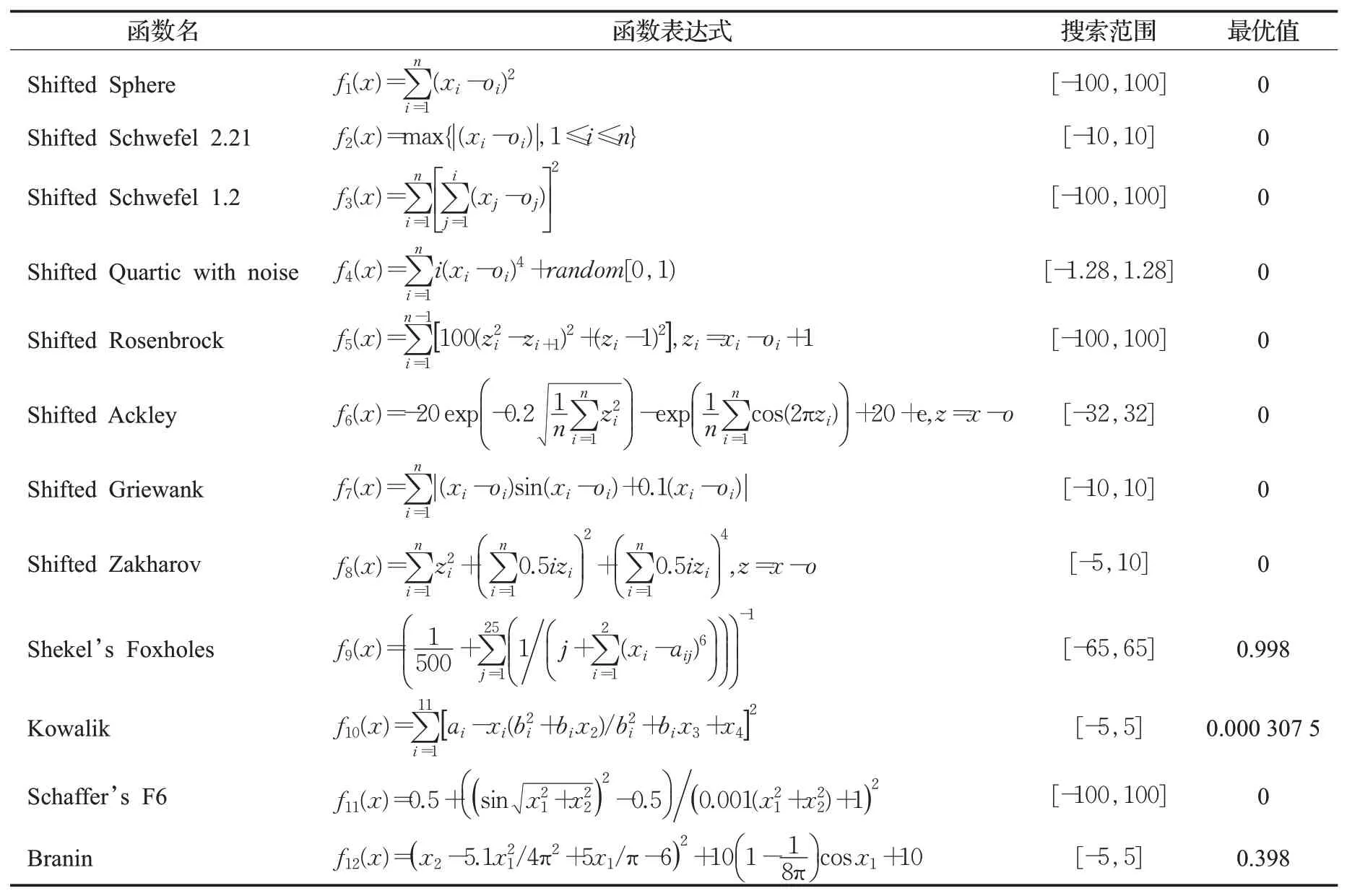
表1 12个基准测试函数Table 1 Twelve classical benchmark test functions

3.2 参数设置及实验结果

实验的种群规模N=50,最大迭代次数为5E+04，位移oi(i=1,2,…,n)在变量范围内随机产生，各算法的实验参数设置如表2所示。为了研究算法在不同维度下的性能，测试函数f1～f8在实验中的维数分别设置为n=10、30、50。为了减小随机误差，每个测试函数都用五种优化算法独立运算30次，记录算法所求得的最优函数值的平均值和标准差，结果如表3～表5所示。

表2 算法的实验参数设置Table 2 Experimental parameter setting

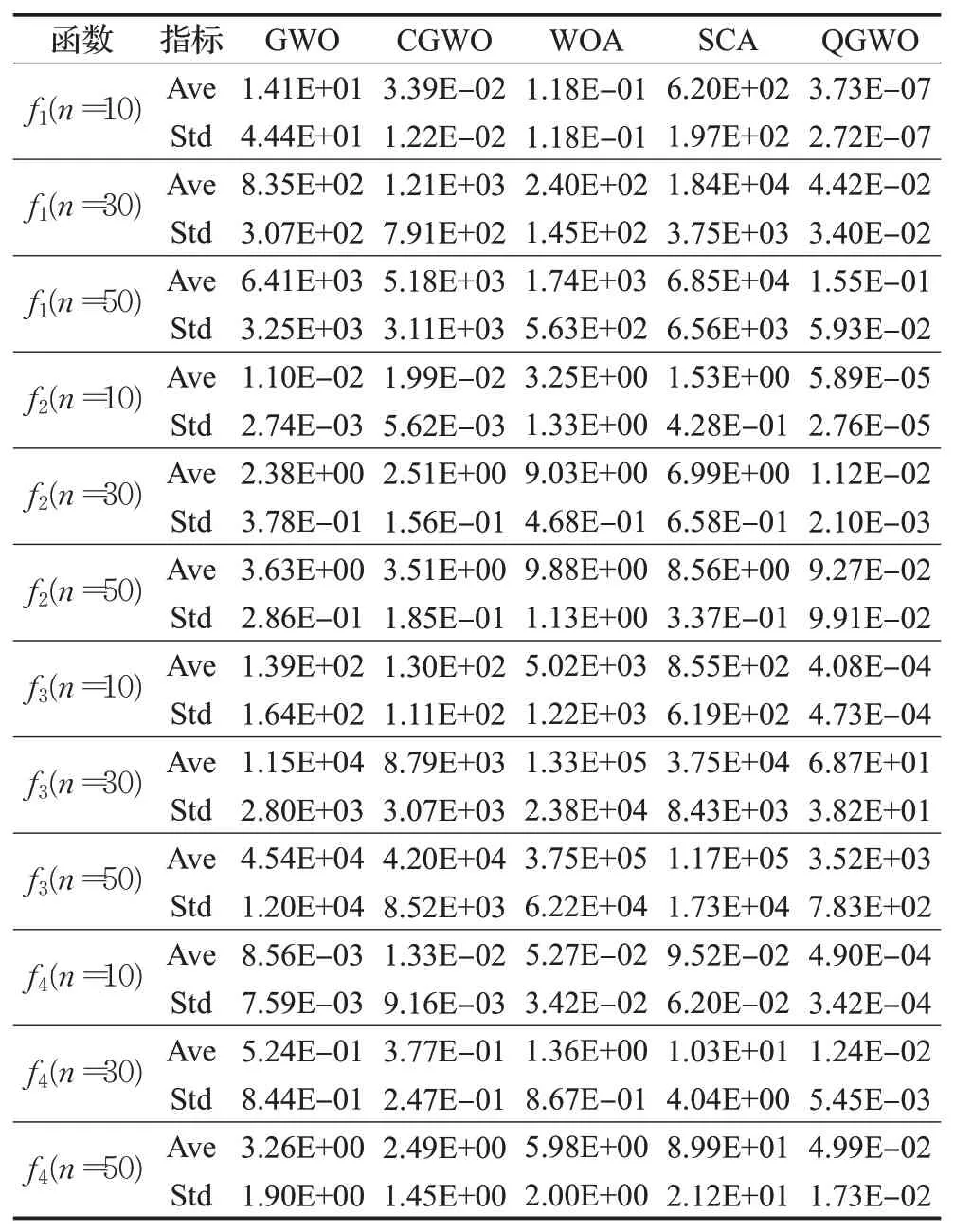
表3 单峰测试函数的求解结果Table 3 Solution result of unimodal test function

从表3～表5可看出，在设定的参数条件下，QGWO与其他四种算法相比，对f1～f12这12个测试函数的求解中，QGWO的求解结果均最小，标准差也最小，说明QGWO具有比其他四种算法更好的求解精度和鲁棒性。当维度n从10增加到30和50时，各算法对测试函数的求解精度和稳定性都有所下降，这是因为维度的增加会使测试函数更复杂，算法求解需做更多的调节。

表4 多峰测试函数的求解结果Table 4 Solution result of multimodal test function

表5 固定维测试函数的求解结果Table 5 Solution result of fixed dimension test function

在算法迭代过程中，记录每次评价的最佳适应度，求出每次评价的平均最优值并绘制曲线，该曲线反映了算法的收敛趋势，因篇幅问题，选取部分函数收敛曲线如图2～图4所示。单峰、多峰的各个函数的收敛曲线趋势基本一致，因此，单峰函数选取f2函数的收敛图，多峰函数选取f6函数的收敛图，固定维函数选取f9、f10、f11来反映改进算法在不同函数上的收敛性。采用本文提出的QGWO对表1的测试函数进行数值实验，并与GWO、正余弦算法[11]（Sine Cosine Algorithm，SCA）、鲸鱼优化算法（Whale Optimization Algorithm，WOA）[12]和改进的灰狼优化算法（CGWO）[13]进行结果对比。

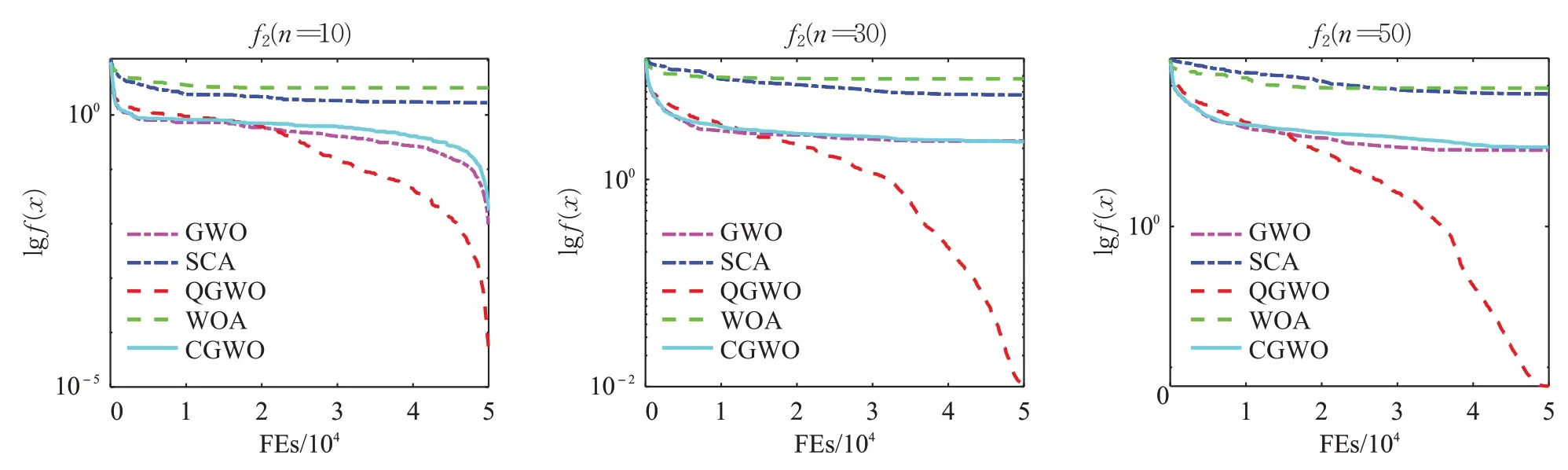
图2 f2函数收敛曲线Fig.2 f 2 function convergence curve

图4 部分固定维函数收敛曲线Fig.4 Convergence curve of partially fixed dimensional functions

从图2可知，求解单峰函数f2时，WOA、GWO和CGWO均过早收敛到局部最优解，而QGWO随着迭代进行继续向目标解收敛。因为控制因子a按照式（9）先快速减小后缓慢减小的非线性变化，先加快了算法的收敛速度以快速的进行全局探索，然后再减缓收敛速度以进行局部搜索，算法引入的量子局部搜索策略，根据式（12）生成的一个吸引点，灰狼种群在以该吸引点为中心进行一维势阱中运动，增加了新个体的多样性，使得灰狼种群的个体具有更好的分布性，最后根据式（14）进行位置更新，进而降低算法陷入局部最优的概率，使得算法具有更好的寻优性能。从图3可以看出，各算法对多峰测试函数f6，在不同的维度的求解结果，WOA、SCA、GWO和CGWO也都过早收敛到局部最优解，只有QGWO继续向最优解收敛。而从表5和图4可知，在对固定维函数的求解中，QGWO均能找到f9～f12的理论最优值，且求解速度和收敛速度都很快。在求解f12时，各算法均能收敛到最优解，但QGWO的标准差最小，鲁棒性更好。

图3 f6函数收敛曲线Fig.3 f6 function convergence curve

为了研究种群规模大小对算法性能的影响，在其他条件不变的情况下，将种群规模大小分别设置为20、50和100。如图5～图7所示是单峰函数f2、多峰函数f5以及固定维函数f9在种群规模分别为20、50和100的收敛曲线，从图5～图7中可以看出在最大迭代次数和位移等条件不变的情况下，种群规模的大小对算法性能的影响比较小。

图5 f2函数实验结果对比Fig.5 f2 Comparison of function experiment results

图7 f9函数实验结果对比Fig.7 f9 Comparison of function experiment results

3.3 模型优化实验

为了验证QGWO算法在求解实际优化问题的性能，将QGWO优化核极限学习机（KELM）[14]与GWO、CGWO优化的KELM以及KELM的分类性能进行比较，采用UCI标准多分类数据集比较这几种方法的性能。从UCI标准分类数据集中选择Breast/Iris/Cancer/Heart四个数据集进行实验训练与测试，其中选用的每个数据集的特征信息如表6。

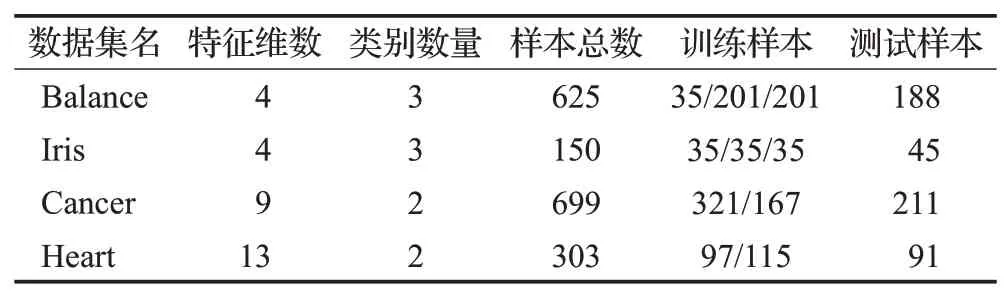
表6 UCI数据集的属性信息Table 6 Attribute information of UCI dataset

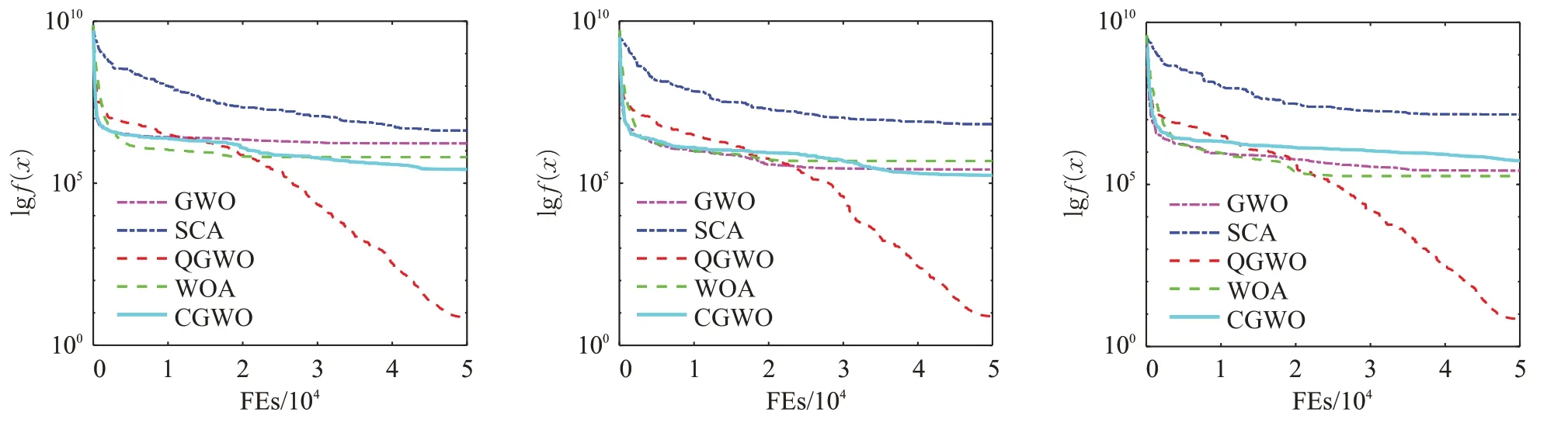
图6 f5函数实验结果对比Fig.6 f5 Comparison of function experiment results

表6 中的数据集训练样本均采用随机选取方式确定，数据集剩余样本作为测试集。由于数据集的不同属性指标间一般因量纲等差异而影响分类器性能，需要对数据集进行归一化处理[15]，计算公式为：

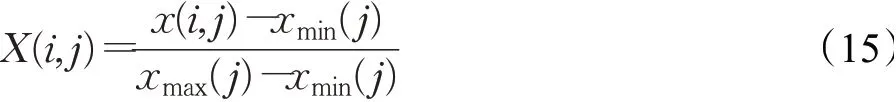
其中，xmax(j)和xmin(j)分别表示第j列的最大值和最小值；x(i,j)和X(i,j)分别表示归一化前后的样本值。

为了验证QGWO-KELM算法有效性，分别用KELM、GWO-KELM、CGWO-KELM和QGWO-KELM在4个数据集上分别采用10次5折交叉验证，将每个数据集分成5份，然后取其中4份作为训练数据集，剩下的1份作为测试数据集，进行实验，取10次结果精度的平均值作为算法的精度，并将最终实验结果与KELM算法、GWO-KELM算法和CGWO-KELM算法进行对比，结果如表7所示。

从表7中的实验结果可以看出，QGWO-KELM算法的分类效果最好，且用时与CGWO-KELM相比更短。QGWO-KELM算法与经典的KELM算法、GWO-KELM和CGWO-KELM算法相比，分类效果均最高，从实验结果可以看出QGWO算法具有良好的优化性能。

表7 分类测试结果Table 7 Classification test results

4 结束语

为了解决灰狼算法求解复杂问题时，存在收敛速度慢，易于陷入局部最优等缺点，本文提出一种基于正弦控制因子和量子局部搜索策略的改进灰狼优化算法。通过12个标准测试函数进行仿真实验，结果表明，本文提出的QGWO算法与其他算法相比，具有更好寻优性能和稳定性；通过四个UCI标准分类数据集进行分类实验，结果显示模型QGWO-KELM具有更好的分类效果，证明改进后的QGWO算法可以有效处理复杂的优化问题。下一步研究内容考虑将QGWO算法应用于铝熔炼生产过程模型的优化问题上。