基于矢量场作用的沥青路面力学模型理论研究

樊丽辉，赵庆国，王新强，孟会林，蓝 清，樊 星

(1.河北省交通勘察设计研究院，河北省石家庄市振岗路120号 050091；2.河北工业大学土木与交通学院，天津市西平道5340号 300401；3.河北水利电力学院，河北省沧州市黄河西路49号 061001；4.河北路合交通科技有限公司，河北省石家庄市建国路661号 050051)

现行沥青路面结构理论的力学分析基本沿用固体力学和工程力学等基本理论，如：剪切应力、弯拉应力、压应力和层间剪切等，以及由此导出强度、应变、弯沉和疲劳等表象参数及由大量试验、经验及评价数据等综合出来的经验公式与回归方程。看似有了整套的路面结构理论——力学-经验法，其实却对大量出现的早期损坏之机理解释感到无能为力，且对沥青路面的控制性、稳定性和耐久性设计更显苍白无力。正如同济大学孙立军所言“沥青路面远比人们所认识的要复杂得多，探索新的理论和新的方法不仅是十分必要的，而且是十分迫切的。”[1]

文中将沥青路面定位为“稳定类混合材料”，而非现行理论所认为的“结构类复合材料”，并将“稳定性”视为沥青路面终极研究目标。以经典力学为参考系，以矢量场为基本点，以场作用的力学行为及内外效应为等效支撑，研究荷载重力场中沥青路面宏观整体稳定性，粒料、沥青及界面微观相对稳定性。将沥青路面与外部因子整合为一个大系统，初步构建起独创的沥青路面力学理论体系——“场作用模型”理论。然后在逻辑推演基础上通过模型应用解析，基本达到逻辑自洽。

1 力学响应及其等效

经典力学认为：力是物体对物体的作用，这种作用会使物体的运动状态或形状发生改变。使运动状态发生改变的作用被定义为“力的外效应”；使物体形状发生改变的作用被定义为“力的内效应”[2]。

荷载重力是物体受到地球引力场作用而产生的竖直向下的矢量作用力，会使沥青路面产生变形，则要研究重力的内效应；会使路面内部的粒料、沥青及界面等发生变位，则要研究重力的外效应。

文中研究的基本路径：采用物理等效方法，研究荷载重力矢量场作用下粒料、沥青及界面的外效应机制，进而研究沥青路面的内效应机制。

1.1 砂粒的物理等效

首先从砂粒层组织形式与力学行为入手，进行力学响应等效分析。

自然堆积砂粒存在流动空间，颗粒较圆砂粒容易滑动，脚踩时会感觉松软。当水分通过氢键使砂粒间形成粘连时，就会结块板实(在刚刚退潮的海滩上行走的感觉)，这是砂粒间介质的键合作用。

由此可推定影响稳定性的三个效应。(1)尺寸效应：尺寸越小，稳定性越差；(2)形貌效应：越接近球形，稳定性越差；(3)介质效应：介质对稳定性有显著影响。

1.2 砂粒层的力学响应

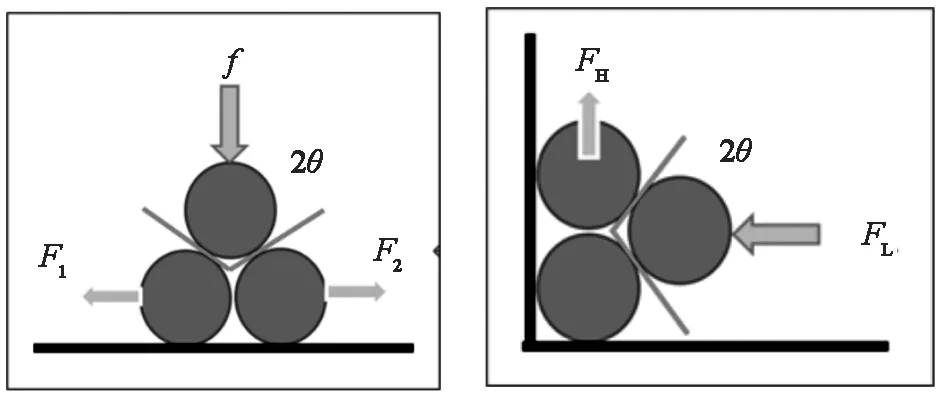
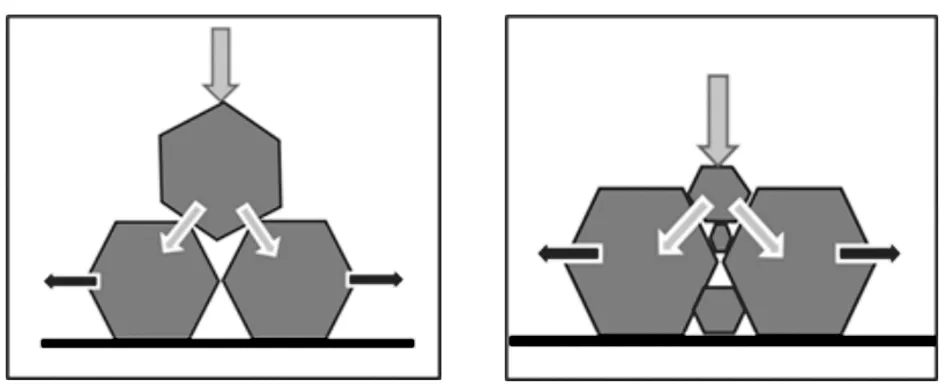
将砂粒视为球形颗粒，当以表观密度形成砂粒层时，其基本构型单元为“等四面体”。为便于分析，可简化为图1所示二维构型。

在荷载重力作用下，上方砂粒会对下方砂粒施加一种“楔形”作用力，使下方砂粒产生横向分力与移位。实际情形是，等四面体构型单元的下方3个砂粒同时产生各自3个方向上的传力行为。文中将这种传力方式命名为“锥楔式”。

锥楔式传力行为包括：砂粒间产生横向分力与变位，以及由横向分力与变位所导致的二次锥楔式竖向分力与变位，如图1(b)和图1(c)所示。由此，可导出图2所示粒料层等效力学响应模型。

(a) (b)

(c)图1 砂粒层“力学传递模型”示意图Fig.1 Mechanical transfer model of sand layer

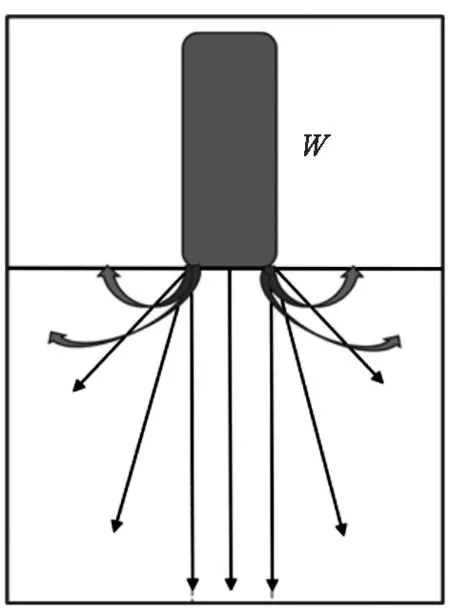
图2 砂粒层“力学响应模型”示意图Fig.2 Mechanical response model of sand layer

图1(b)所示，由横向分力FL产生的二次锥楔式传力方式，所导致的竖向分力FH，考虑摩擦系数δ，可表示为：

(a)

(b) (c)图3 碎石层“力学传递模型”示意图Fig.3 Sketch map of mechanical transfer model of crushed rock layer

FH=δ×(FL×cosθ)×cosθ

由此可得出尺寸效应重要推论：粒径越小，楔形作用力越大，越易产生变位，稳定性就越差。

1.3 碎石的物理等效

将碎石视为“不规则多面体”，其堆积通常会形成许多面与面相接触的构型单元，尤其图3(a)所示的竖向叠摞情形，在荷载重力作用下，碎石间形成上下互为支撑的传递模式，其特征在于下层碎石产生横向分力的几率很小。文中将这种传力方式命名为“叠摞式”。

当然，碎石层中也会存在锥楔式传力行为，如图3(b)、图3(c)所示，但在力学响应上会显著滞后于球形砂粒。实际上，碎石层传力模式应当属于以叠摞式为主的混合传递模式。而图3(c)已经涉及到级配碎石概念。

1.4 碎石层的力学响应

碎石的粒径、形貌和级配等都会影响碎石层传力模式。若以锥楔式为主，则为不稳定状态；若以叠摞式为主，则稳定性较好，粒料间不易发生变位。

因此得出碎石层稳定构型：“以大粒径碎石形成叠摞主体骨架结构，小粒径砂粒仅仅嵌存于骨架缝隙内，不参与力的传递行为”。

1.5 沥青路面之力学响应

对于沥青路面，将沥青视为介质进行等效分析，既要考虑粒料间力学行为与响应，又要考虑沥青的热力学行为。

通常，粒料在重力场中沿力场方向产生向外的发散变位趋势，而沥青介质，一是对粒料发散变位产生阻滞阻尼作用，二是会沿力场方向产生向内的收敛变位趋势。这两种变位均具备单向度特征，并且，粒料发散变位是起因，沥青收敛变位是结果。可类比于轻轻拍打湿润沙滩时水分会慢慢浮上砂面情景。

粒料与沥青外效应是起因，属于微观矢量变位。从而引起沥青路面内效应——宏观有序变形[8]。

2 矢量场作用原理

这里给出几个新概念：重力场矢量、场势能、场通量及做功等。[6-7，9]

2.1 荷载重力场

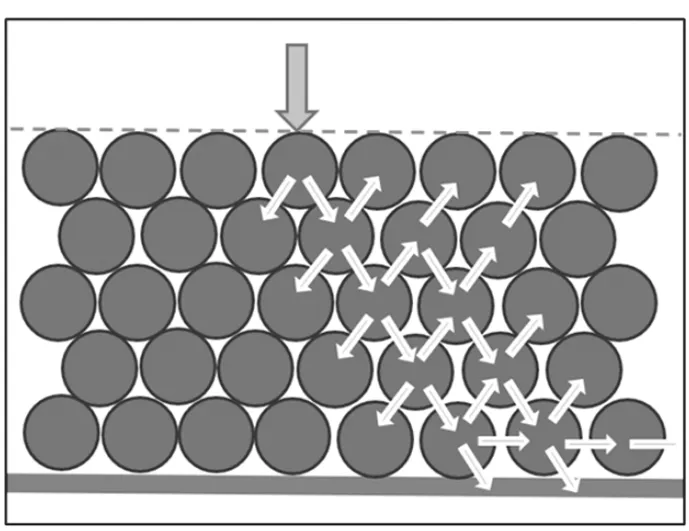
车辆荷载作用于沥青路面，其重力矢量场作用模型见图4。

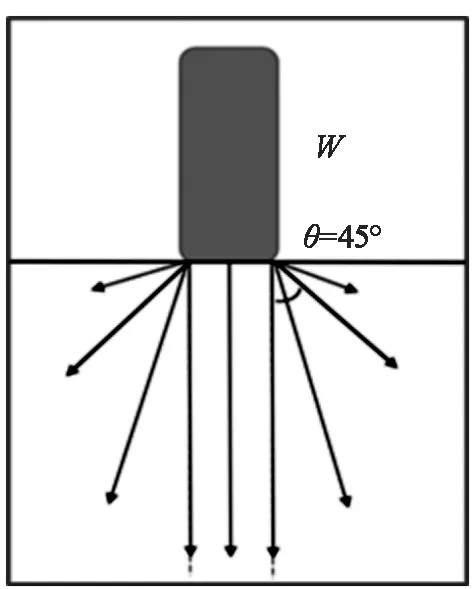
图4 重力矢量场作用模型示意图Fig.4 Schematic diagram of gravity vector field action model

这里引入“重力场通量”概念，用于描述某粒料所受到场作用强度，其大小与方向遵循“距离平方反比定律”和“余弦法则”。

重力场中任意受力点ds受到的压强为：

那么某粒料(ΔS)受到的重力场通量fΦ为：

(1)

式中，dW/dS为荷载压强(标准值为0.7MPa)；r为粒料与轮胎接地面间距；θ为侧压方向与竖直方向间夹角。

2.2 重力做功

对于沥青路面，无论是车辙还是开裂，究其本源均属于粒料、沥青介质在重力场作用下产生了变位与做功(力的外效应)。

经典力学中恒力的功等于力与受力质点位移的标量积。由于粒料及介质变位通常为微位移，应研究重力的元功。即力与受力质点的元位移dr的标量积[2]：

dA=F×dr=F×|dr|cosθ

(2)

对于粒料，通常存在2种做功形式：平动和转动。而对于沥青路面而言，其做功行为包括2大类：一是压路机压实做功；二是车辆轮荷再做功。

2.2.1 压实做功

钢轮压路机可视为“线形荷载”，属于“横向分力=0”的约束性压实做功模式(见图5)。这势必会发生横向不均衡压实做功，带来局部密实缺陷。尤其摊铺厚度较薄、混合料离析等，摊铺时很容易发生松铺差异，导致横向初始密度不一致。而钢轮横向约束性压实做功，又恰恰很难克服这种横向初始缺陷。

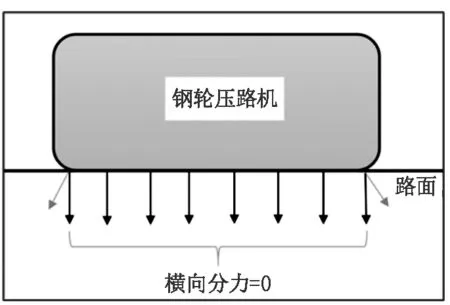
图5 钢轮压路机压实做功示意图Fig.5 Schematic diagram of compaction work of steel wheel roller

为此，文中提出“横向均衡压实作业方式”，其主要原理为：初压时钢轮呈锐角(如45°角)行进，既能解决路面横向缺陷问题，又能较好保证路面平整度。

2.2.2 轮荷再做功

相对于钢轮压路机，轮胎荷载可视为“点荷载”，属于“横向分力≠0”的无约束性压实做功，必然会产生再做功行为。

锥楔式会成为轮荷再做功的内因，而初始密实缺陷区域会成为早期发生再做功的重点部位。

文中归纳出沥青路面车辙和Top-Down裂缝(以下简称：TDC)病害产生的5个必要条件：①横向分力≠0；②存在锥楔式传力行为；③沥青介质存在高温润滑行为；④油石界面存在水损坏问题；⑤粒料尺寸、形貌与级配存在不利因素。

以上除第1条无法避免外，其余4条在技术上均预先可控。

2.3 沥青介质

介质的物理功能主要有：传递、润滑、流动、黏结、固定、阻尼等。沥青作为介质，其正向功能包括传递、黏结、固定、阻尼等；而润滑与流动则为负向功能。用沥青作为介质应遵循的原则：高温状态下不出现润滑和流动态势。

作为黏弹性材料，沥青及沥青路面力学性能在很大程度上取决于荷载重力场作用时间t(或次数)。其定性关系为：①t极短时呈刚性；②t较短时呈弹性；③t较长时呈黏滞性并伴随塑性；④t很长时呈塑性(流动性)；⑤t处于中间时段时，既表现为弹性又伴随黏滞性。通常，沥青路面受到车辆荷载作用时间(次数)属于“中间时段”。

2.4 油石界面

在荷载重力场作用下油石界面会产生分子尺度的矢量化微观变位，并可累积到沥青路面宏观有序变形。

油石界面出现水损害，会在界面区形成分子尺度水膜，一方面是石料表面悬键对水分子产生化学键合，并区分于硅质石料和钙质石料[8]；另一方面是水稳碎石基层(或桥面水泥混凝土铺装层)与沥青面层之间的超级油石界面水损害。

油石界面水损害，一是界面力学性能会大大降低；二是水分子隔膜会大大增加界面润滑性与推移做功行为。

文中将此命名为“界面效应”。

3 沥青路面场作用模型

3.1 重力场势能

依据表达式(1)，轮迹正压区重力场通量为：

而轮迹侧向各角度产生的横向分量fΦθ为：

fΦθ=fΦ0×cosθ×cos(90°-θ)

(3)

那么，在等距作用面上轮迹侧向呈45°角的横向分量为最大值，即：

fΦθ=0.5fΦ0

以现行高速公路典型路面结构(上中下面层及路面基层)进行矢量场势能分布分析。

如图6和图7所示，假设以45°角为重力场辐射等势面，实质上可视为荷载重力场传递等效面。即：

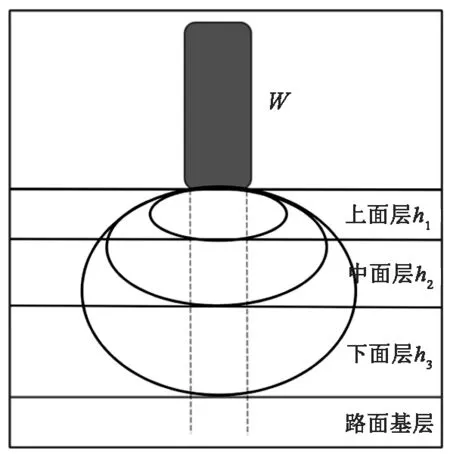
图6 重力场势能分布示意图Fig.6 Schematic diagram of potential energy distribution in gravity field

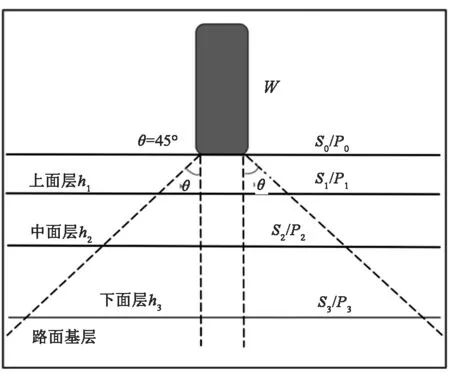
图7 沥青路面重力场等效面示意图Fig.7 Schematic diagram of equivalent surface of gravity field of asphalt pavement

P0×S0=P1×S1=…=Pn×Sn=W

(4)

式中，P0，P1，…，Pn为作用压强；S0，S1，…，Sn为作用面积；r0为轮胎接地面直径(假定为圆形)；h1，h2，…，hn为与路表面的距离；rn=r0+2hn。

由式(4)分析可知：

(1)各等势面Pn与r0的平方呈正比关系。这表明：重型车对下层产生的破坏作用远大于轻型车。

(2)各等势面Pn与hn的平方呈反比关系，其衰减速率较大。这表明：荷载重力场对表面层的破坏作用较大，进入下面层或基层后的破坏作用会大大减弱。

假设某路面参数为：h1=40mm，h2=100mm，h3=200mm，计算其重力场势能。

例1：假定某重型车轮胎接地直径r0=30cm，则各层等势面衰减值为：P1=P0/1.6；P2=P0/2.8；P3=P0/5.4。

例2：假定某轻型车轮胎接地直径r0=20cm，则各层等势面衰减值为：P1=P0/2.0；P2=P0/4.0；P3=P0/9.0。

由上述计算得出推论：

①相同的轮胎接地压强，重型车的重力场衰减速率明显较弱。这表明：重型车对路面各层的作用强度显著大于轻型车；

②因严重超载(P0≫0.7MPa)所产生的附加破坏作用不遵循场衰减规律，会直接传递到各面层和基层。

3.2 路面系统自由度及稳定度

3.2.1 自由度模型

借用物理学系统自由度概念，对沥青路面系统进行物理描述。

自由度是指对系统结果产生影响的独立变量的数量。文中重点讨论运动自由度，例如：①一个刚体在三维空间运动，就存在3个平动自由度t=3和3个转动自由度r=3，即刚体的自由度为i=t+r=6；②一个大分子，它的每一个原子都存在3个平动、3个转动和3个振动[5]。

举例：将粒料视为刚体，其在路面空间内的运动自由度为i=t+r=6；再将层间界面视为二维运动坐标系，则一个路面系统的粒料自由度为S=N·i+2(S为路面系统自由度，N为粒料数量，2表示二维层间)。

在多种尺度元素混成的沥青路面系统中，必须引入微观物理量自由度，如：沥青大分子自由度、油石界面自由度、界面水分子膜自由度，等等。另外，还需引入2个重要影响因子：热力学自由度——温度T；动力学自由度——荷载重力F及作用时间t(或次数)。

至此，可初步给出沥青路面系统自由度模型：

S总=[S粒+(S介+S界×S水)×T]×(F×t)

(5)

其物理意义：对于沥青路面系统内一个等效单元，系统自由度S越小，路面系统就越稳定。式(5)中各项的具体含义如下。

(1)动力学自由度(F×t)：代表微观变位矢量化与宏观变形有序化的物理意义。

(2)热力学自由度(T)：代表分子尺度海量化与宏观物理量实时响应的物理意义。

(3)界面及水分子自由度(S界×S水)：代表油石界面与路面耐久性的物理意义。

(4)介质自由度(S介)：代表黏弹性动力学与路面稳定性的物理意义。

(5)粒料自由度(S粒)：代表骨架力学行为与路面整体稳定性的物理意义。

3.2.2 稳定度模型

在自由度概念与模型基础上，文中给出“稳定度指数D”的概念，即指综合考虑影响沥青路面稳定性的诸因子作用程度及相互依存关系的物理描述。通过稳定度指数的量化推演，初步实现沥青路面稳定性的定量化预判。初步的“稳定度模型”：

(6)

式中，Dgj为骨架指数(代表骨架主体结构)，为“2倍平均粒径/层厚”；Dxm为形貌指数(代表大骨料形貌)，多面体为1、球形为0、中间值可选；Djz为介质指数(代表介质性能)，改性沥青为1、基质沥青为0.5；Djm为界面指数(代表油石界面微结构性能)，界面处理为1、未处理钙质为0.5，未处理硅质为0；Tx为温度系数(代表温度区间)，高温为2、常温为1、次低温为-1、低温为-2；Wx为荷载系数(代表荷载类型)，轻型车为2、标准轴载重车为1、超载重车为0.5。

那么，D值越大，路面稳定性越高，耐久性越好。以下选取几例典型沥青混合料及路面，尝试进行D值计算：

①两层大骨料改性沥青界面处理标准轴载：D=±1；

②两层大骨料基质沥青界面不处理标准轴载：D=±0.5；

③普通沥青AC-13沥青混合料界面不处理标准轴载：D=±0.1；

④改性沥青AC-13沥青混合料界面处理标准轴载：D=±0.2；

⑤沥青砂：河砂基质沥青界面不处理：D≈0。

3.3 “场作用模型”理论原理

3.3.1 四个效应

文中提出影响沥青路面稳定性的四个效应：

(1)尺寸效应——粒料粒径越小，越易做功，越发不稳定，且所需作用力越小；

(2)形貌效应——粒料形貌会直接影响传力模式，球形最不利；

(3)介质效应——高温流动与低温脆性，均为沥青介质负向功能；

(4)界面效应——油石界面水损害会增加界面自由度，降低界面力学性能。

综合来看，“粒径小、球形貌、介质滑、界面糟”属于极不稳定状态。后三项均可预控，唯有第一项成为沥青混合料及路面稳定性设计的关键参量：尺寸效应成为终极追问。

3.3.2 三个模型

矢量场作用、系统自由度和稳定度等三者之间形成并基本实现理论互恰、有机契合和逻辑融洽。

(1)“粒料力学行为与响应模型”——解析粒料尺寸、形貌及力学行为与稳定性等效机制与原理。

(2)“重力场通量与场势能模型”——解析荷载重力场对沥青路面作用机制与破坏行为机理，初步建立沥青混合料与沥青路面间的桥联机制。

(3)“系统自由度与稳定度模型”——解析荷载重力场作用下沥青路面系统稳定机制，引入各类影响因子，初步建立微观与宏观间的关联机制。

3.3.3 四个推论

(1)粒料、沥青介质及界面的微观矢量变位是起因，沥青路面宏观有序变形是结果。

(2)重型车重力场通量与场势能衰减速率显著小于轻型车，重型车严重超载所引起附加破坏作用，不遵循重力场衰减规律。

(3)荷载重力场中粒料产生正方向发散变位做功，而沥青介质则产生反方向收敛变位做功。

(4)水分子作用于油石界面，一是沥青膜剥离加速介质疲劳进程，二是水分子隔膜作用大大增加界面微观变位及做功。

4 场作用模型之应用解析

结合沥青路面典型结构及破坏情形，进行场作用模型应用解析，以检验其普适性及合理性。

4.1 粒料选用原则

图8为某沥青路面上面层(AC13)剖面照片。该沥青混合料满足现行规范的空隙率、马歇尔稳定度等性能指标要求。

图8 沥青路面剖面图(AC-13密级配)Fig.8 Cross section of AC-13 dense graded asphalt pavement

在荷载重力场作用下该沥青路面上面层表现：①这种密级配型沥青路面内部存在粒料间锥楔式传力行为；②其稳定度指数D的计算值很小，仅为0.1。这就为密级配沥青混合料所表现出的普遍性早期病害现象，提供了机理解释，从而得出结论：密级配沥青混合料本就属于一种“不稳定混配材料”。

故此，多少年来人们无论曾经怎样对这种密级配型沥青混合料进行优化设计与实验研究，均始终不得要领。

对于骨架密实型级配、悬浮密实型级配和骨架空隙等等，只要存在级配，就会存在锥楔式传力行为，也就存在不稳定性。

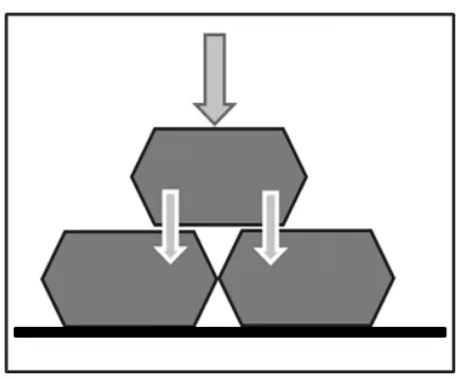
图9所示的球形粒料一旦形成2层以上叠放，就必然出现横向分力与推移。而2层碎石叠摞的横向分力尚不明显，但3层以上碎石的横向分力及推移做功就在所难免。

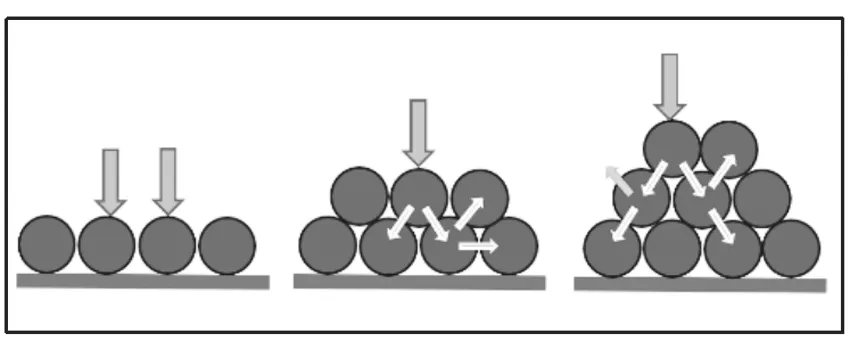
图9 粒料叠放等效示意图Fig.9 Equivalent diagram of granular stacking

鉴于此，基于稳定性研究目标，文中提出2个粒料选用原则：①以大骨料构成“骨架主体结构”原则；②细集料粒径选取以不影响骨架主体结构为原则。

这里，“大骨料”选用粒径为层厚H的H/3～H/2的石料档，目的是限制叠摞层数；“细集料”选用粒径小于H/20的机制砂，并以其掺配量来调控空隙率指标。其意图在于：将机制砂对骨架主体结构的尺寸效应影响限制在10%以内。

总之，该原则属于“大骨料叠摞式主体结构之机制砂配位”，明确限定大骨料与细集料尺寸效应量级，以满足场作用模型理论“骨架主体结构”原则。文中将其命名为“稳定型沥青混合料(WD)”。所谓“稳定型沥青混合料”，原理在于其粒料间可以形成稳定的“固架结构”，最大限度地克服荷载重力场作用下粒料与沥青的微观变位及沥青路面的宏观变形，从而构成稳固持久的“稳定型沥青路面”。

4.2 足尺加速加载试验之场作用解析

文献[4]指出：①“轮隙间裂缝”和“轮迹带外边缘裂缝”都为TDC裂缝，且深度较浅，仅出现在上面层内，见图10(a)；②当达到一定加速加载作用次数后，轮迹带边缘处开始出现纵向裂缝，路面厚度越薄的结构越容易出现开裂且裂缝宽度发展越快；

(a)[4]

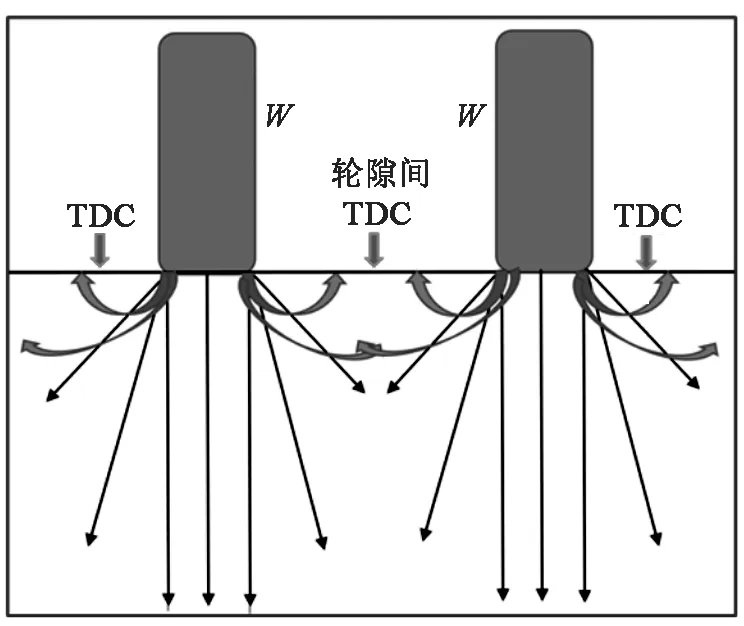
(b)图10 “足尺加速加载试验”轮隙间裂缝及其力学响应示意图Fig.10 Wheel gap crack and its mechanical response diagram of “full scale accelerated loading test”

③加速加载作用对上面层混合料疲劳抗力的影响，比中下面层沥青混合料更加显著；④上面层混合料的疲劳抗力随加载作用次数增加而衰减的程度，相比中下面层混合料更显著。

图10(b)为场作用之力学响应示意图，文献[4]给出的4条结论，恰好成为“场作用模型”理论普适性的有力佐证。

(a) (b)

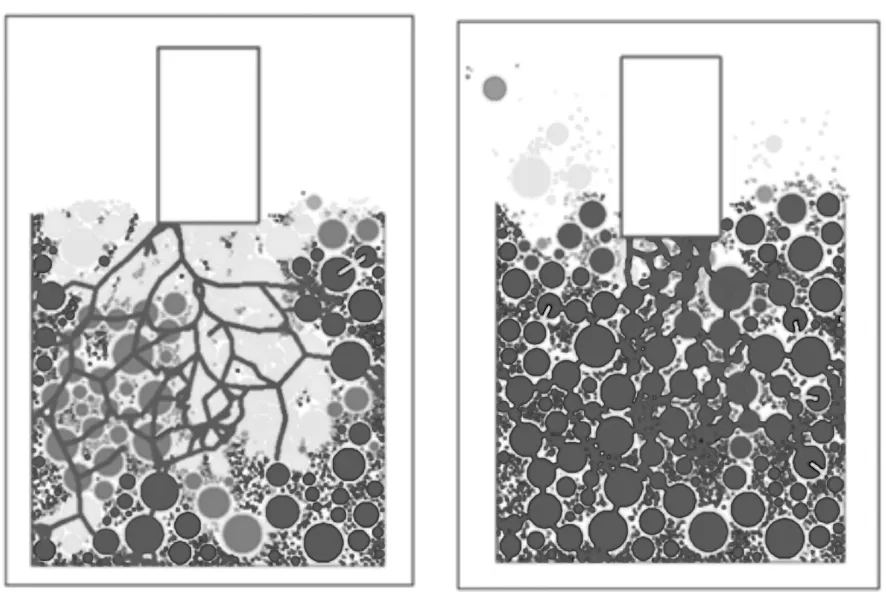
(c) (d)图11 二维离散元模型分析示意图Fig.11 Schematic diagram of two dimensional discrete element model analysis

文献[4]结论之第1、第2条可由荷载重力场之力学响应模型给予机理解释；第3、第4条可由荷载重力场通量与场势能模型给予机理解释。

4.3 桥面铺装层之场作用解析

桥面沥青混凝土铺装层通常存在两个薄弱环节：一是摊铺厚度较薄、混合料离析等；二是横向不均衡密实缺陷。从而造成桥面早期病害发生几率普遍高于路面，如：开裂、松散、坑槽、拥包、波浪等。

一方面，在与水泥混凝土铺装层界面区，由于受到竖向刚性约束，粒料及粘层油会将轮荷重力场中侧向作用力的大部分转为横向分力及推移做功；另一方面，粘层油与水泥混凝土铺装层之间的超级油石界面，发生水分子膜剥离，荷载反复作用加大推移做功行为——低温开裂，高温车辙。

需要特别指出：此应用解析也完全适用于采用“强基薄面”理念的普通等级公路。以水泥稳定碎石为半刚性路面基层，其强度、刚度、表面状况及物理属性，包括上下两层的沥青路面结构，与桥面铺装层设计基本近似。故此，基本廓清了我国普通沥青公路一直存在耐久性不足(寿命仅3～5年)的问题根源与机理所在。

4.4 层间黏结之场作用解析

层间黏结的传统认知是：提高沥青结构层间结合力，传递层间剪切应力及压应力；并认为，层间联结程度对整个路面结构疲劳寿命有非常显著的影响[3]。

文中已将沥青路面定位为稳定类混合材料，那么，路面结构层、层间黏结及粘层油就失去了其自身物理意义。相反，粘层油的存在很可能会带来更多负面作用。

层间黏结相当于增加了层间隔离介质层，变相加大了局部油石比。夏季高温路表温度通常可达60℃，面层下4cm处与路表温度相差不大，且重力场势能衰减尚不显著，势必会加大层间区域粒料及沥青介质横向推移及做功行为。

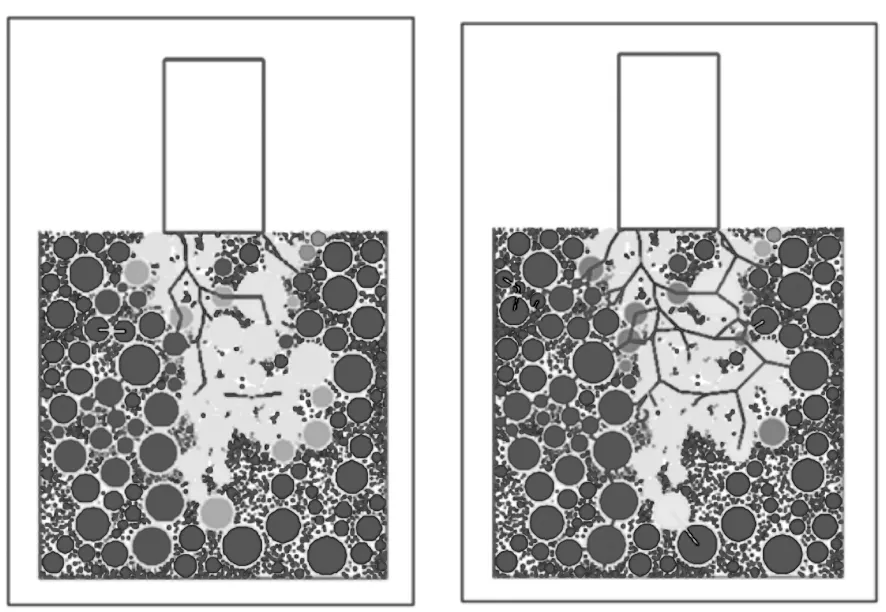
4.5 离散元分析

离散元分析[10-12]，以单轴贯入试验为例，生成二维离散元模型。在荷载作用下，模拟不同阶段集料颗粒内部力链分布情况。

加载初期(图11a)，颗粒内所产生的力链数量仅62条；加载1/3期(图11b)，颗粒间力链为235条，形成网状力链结构，荷载作用区内的颗粒产生较大位移，荷载作用区周边的颗粒产生向上的作用力；加载2/3期(图11c)，颗粒间力链数量增至345条，荷载作用区周边颗粒向两侧推移，产生向上位移现象，并产生松动，形成不稳定平衡状态；加载末期(图11d)，力链数量增至526条，形成多个网状结构体系，作用区两侧颗粒已脱离了试件，出现了分散现象。

由此得出：整个数值模拟分析与“场作用模型”理论形成了相互印证。

5 结束语

基于静力学、矢量场和系统自由度等经典物理原理，初步形成了沥青路面力学之场作用模型理论体系，并通过逻辑推演与应用解析，初步验证了该体系的理论普适性和逻辑缜密性。

(1)“粒料力学行为与响应模型”、“重力场通量与场势能模型”和“自由度与稳定度模型”等三大模型构建起“场作用模型”理论体系。

(2)基本廓清了影响沥青路面稳定性的四大效应：尺寸效应、形貌效应、介质效应及界面效应。

(3)由场作用模型及其应用解析，得出重要结论：级配型沥青混合料属于“失稳型沥青混合料”。

(4)研究设想：引入振动动力学、摩擦力学、路面纵横坡度几何参量、环境作用诸因子以及材料性能与组成等，进一步研究完善场作用模型理论体系，并同时开展技术应用体系研究。