高压捕获翼构型亚跨超流动特性数值研究1)

王浩祥 李广利 杨 靖 肖 尧 王小永 *徐应洲 许先贵 崔 凯

* (中国科学院力学研究所高温气动国家重点实验室，北京 100190)

† (中国科学院大学工程科学学院，北京 100049)

引言

高超声速飞行器近年来已成为国际研究热点，以美国为代表的发达国家先后开展了大量研究[1]-[3]，其中高超声速飞机[2]因具有水平起降和宽速域飞行等优势，在军事和民用方面均具有巨大潜力.2013 年，美国洛克希德-马丁公司公布了SR-72 高超声速无人侦察飞机概念[4]，以此作为SR-71 的后继机.2018 年，波音公司在美国航空航天学会科技大会上，公开展示了一个侦察/打击型高超声速飞机模型和初始概念方案以及相关技术细节，这是美国首次公开高超声速民用飞机领域进展动向[5].2019年5 月，美国的Hermeus 公司披露要研制最大巡航速度马赫5、载客20 人左右、航程4000 海里的高超声速民用飞机，并计划在21 世纪20 年代末投入商业运营.欧洲联合俄罗斯、澳大利亚和巴西等国，以高超声速民用飞机为方向，开展了Hexafly-Int 研究计划[6].日本学者Lobbia 等以乘波体为基础提出了一种高超声速商用飞机等概念[7].同时，国内学者针对高超声速气动外形也展开了相关研究，分别提出了旁侧进气[8]和背部进气[9]等先进气动布局方案.从现有研究结果来看，关于高超声速飞机的研制仍处于概念探索阶段，距离真正的实际飞行和商业运营还有着较长的发展道路.

从气动布局设计角度来看，高超声速飞机主要追求的性能指标包括高升阻比、高升力系数和高容积率.然而上述性能指标之间存在着强烈的矛盾关系，对于常规构型而言，容积的增大通常会导致升力系数和升阻比的降低，而且在高超条件下还存在“升阻比屏障”[10]问题，使常规构型很难同时满足“三高”需求.针对上述问题，崔凯等[11-12]提出了一种高压捕获翼新型气动布局概念，其基本原理是通过在机体上方引入捕获翼的方式，来改变机体激波的传播方向，利用机体与捕获翼之间的气动干扰来产生高压区，进而提升整机的升力与升阻比.目前针对高压捕获翼新概念构型的研究主要集中在高超声速条件下的性能评估与设计方法研究，如捕获翼位置的确定方法[13]、捕获翼前缘线外形优化[14]和高升阻比外型设计[15-16]，研究结果表明高压捕获翼气动布局可在高超声速条件下有效缓解升阻比与容积率、升阻比与升力系数间的矛盾关系，具有较好的应用前景，为未来高超声速飞机气动布局设计提供了新的思路.

对于水平起降的高超声速飞机而言，不仅要关注巡航状态下的高速性能，还需关注飞行过程中其他速域的气动性能.在亚、跨、超、高超声速飞行条件下，飞行器的流场结构会发生明显改变，导致其气动性能出现较大差异[17].针对上述问题，Zhao 等[18]总结了几种宽速域乘波体设计方法以提升其在非设计点状态下的气动性能;罗浩等[19-20]和焦子涵等[21]提出了几种宽速域变构型高超声速飞行器，通过连接装置的收放改变飞行器的展弦比和后掠角，以此来兼顾高低速的气动性能;孙祥程等[22]和张阳等[23]通过优化算法得到新翼型，研究结果表明，该翼型相比于常规的高超声速翼型，在跨声速和高超声速下具有更加优良的气动特性，配置新翼型的机翼在宽速域范围内整体气动性能更优;Zhao 等[24]中对几种乘波体在亚跨超飞行条件的气动性能进行了综合比较，结果表明在亚跨超飞行条件下尖前缘乘波体升阻比要优于通常的密切锥乘波体，三角翼乘波体除小攻角和负攻角外升阻比也优于普通的密切锥乘波体，此外通过比较尖前缘乘波体在亚跨超飞行条件下能够产生更大的涡升力.综上所述，对于水平起降和宽速域飞行的高超声速飞机，开展亚、跨、超飞行条件的气动性能研究是十分必要的.

由高压捕获翼的设计原理[13]可知，捕获翼置于机体上方，在机体与捕获翼之间会形成一个开放的等效通道，在高超声速设计点状态下，机体激波经过捕获翼后所形成的反射激波刚好掠过机体尾部，此时机体基本不受捕获翼干扰.但在亚跨超条件下，流场结构会发生本质改变，随着马赫数的增大，通道内气动干扰会逐渐增强，会出现类似于Busemann 双翼构型在低速下的壅塞现象[25-26].为研究高压捕获翼构型在宽速域内的流动特征，王浩祥等[27]基于高压捕获翼概念构型对马赫0.92 条件下的流场结构进行了细致分析，结果表明通道的压缩-扩张会造成机体转折点与尾部之间产生较大的压差，导致圆台上表面产生分离区，机体后半段处产生的激波与分离区作用会产生二次激波，机体与捕获翼的流场会耦合在一起，使整机的流场结构变的复杂，并且激波串会导致捕获翼下表面的物面压力出现明显的波动现象，初步证实了跨声速条件下，高压捕获翼构型存在复杂的流场结构和较为强烈的气动干扰特性，因此有必要对高压捕获翼构型亚跨超速域流动特性展开更加深入的研究.

基于上述研究背景，本文在文献[27]的基础上，基于一种简化的高压捕获翼概念构型，对高压捕获翼气动布局在亚跨超典型来流条件下的流动特性展开细致研究，重点关注机体与捕获翼之间开放通道内流场结构随马赫数的演化机理，以及其对飞行器壁面的压力分布影响特性.以期为后续宽速域飞行器气动构型设计与优化奠定坚实基础.

1 高压捕获翼原理和计算模型简介[27]

高压捕获翼在高超声速流动条件下的设计原理如图1 所示，图中区域①为自由来流，高速来流经过机体上表面压缩，产生第一道斜激波S1，在激波S1后压力增加，流动方向与机体上表面平行，之后在捕获翼的压缩作用下形成第二道激波S2，使压力获得进一步提升，随来流继续前进，在机体尾部产生膨胀波，经前马赫线(FML)后压力逐渐减小，然后流向下游，由于捕获翼平行于来流，区域⑤的压力基本与自由来流压力相等.由上述描述可知区域③经两次压缩，捕获翼下表面的压力明显高于上表面，因此捕获翼可为飞行器提供较大的升力，当采用薄翼设计时，其阻力增加较小，飞行器的升阻比也可获得大幅提升.

图1 高压捕获翼设计原理Fig.1 Design principle of the HCW

为突出重点，本文依据上述设计原理采用了一种简化外形，使用一个圆锥-圆台组合体作为概念机体，在其上方设置高压捕获翼，其外形为具有一定厚度的平板，前缘进行钝化.外形主要参数如下:机体长L为1.5 m，以机体长度为参考量，无量纲化的捕获翼相对长度为0.431;相对宽度为0.333;相对厚度为2.667 × 10-3.捕获翼与机体间的相对位置依据文献[13]中的捕获翼位置设计方法给定.按上述方法生成的计算模型如图2 所示.

图2 构型三维视图和三视图Fig.2 Three-dimensional and three view of the configuration

为验证该构型的效果，在设计条件下对其流场进行了计算，条件如下:来流马赫数为6，单位长度雷诺数为2.258 × 106m-1，飞行攻角为0°.图3 给出了该构型在设计条件下的物面和纵向对称面压力云图，从图中可以看到，机体压缩产生的激波打在捕获翼前缘附近，并且反射激波刚好掠过机体最高点，符合高压捕获翼构型的基本设计原则.

图3 纵向对称面的压力分布云图Fig.3 Pressure contour in the symmetrical plane

2 CFD 可靠性验证与计算外形数值求解

本文数值模拟基于可压缩流动N-S 方程，数值方法采用TVD (total variation diminishing)格式，时间推进选用隐式格式，湍流模型为SST 模型.为验证CFD 数值方法的可靠性，分别计算了跨声速翼身组合体标模、超声速航天飞机标模和超声速激波边界层干扰典型案例.

图4 为翼身组合体的结构网格示意图，其中壁面法向第一层网格厚度为S(× 10-5)，其中S为翼身组合体总长度，总网格量约1100 万.计算马赫数为0.75，单位长度雷诺数为2.125 × 107m-1，攻角为0.49°.图5 给出了机翼不同展向截面的压力系数Cp随x/c的变化曲线，其中x和y分别代表流向距离和展向距离，c为弦长，b为机体半模展长，下同.计算结果表明，CFD 计算结果与风洞试验数据[28]基本保持一致，且能够比较精确的预测出激波出现的位置.

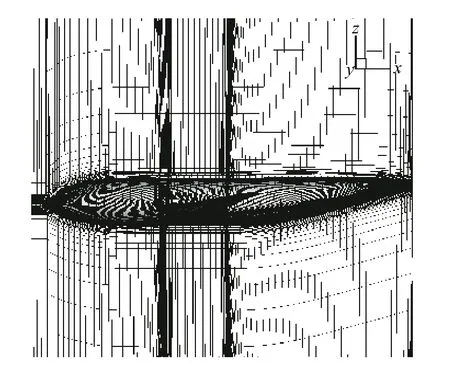
图4 翼身组合体结构网格示意图Fig.4 Illustration of structure grid of wing-body combination

图5 机翼不同展向位置压力系数Cp 变化曲线Fig.5 Curve of Cp at different spanwise section of wing

图6 给出了航天飞机结构网格示意图，其中壁面法向第一层网格厚度为H(× 10-5)，其中H为航天飞机总长度，总网格量约1024 万.计算马赫数为4.94，单位长度雷诺数为3.15 × 107m-1，攻角为0°.图7 给出了典型截面物面压力系数对比结果，其中c表示y/H=0.13 处截面机翼弦长，计算结果表明，CFD 计算结果与风洞试验数据[29]吻合良好.

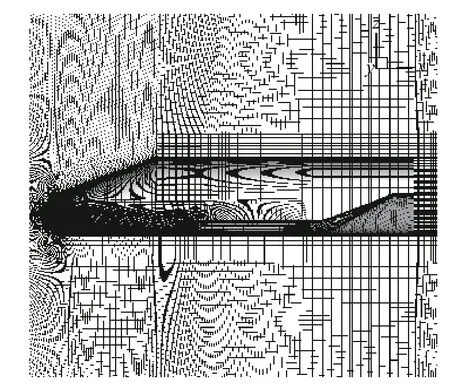
图6 航天飞机结构网格示意图Fig.6 Illustration of structure grid of space shuttle

图7 航天飞机机身物面压力系数Cp 变化曲线Fig.7 Curve of Cp at different spanwise section of space shuttle

此外为验证当前所使用的CFD 求解器对于激波的模拟精度，计算了典型的激波边界层干扰构型.该构型由两部分组成，分别是上方的楔形平板和下方的圆锥-圆柱组合体.图8 给出了结构网格示意图.其中壁面法向第一层网格厚度为W(× 10-5)，其中W为圆锥-圆柱组合体长度，总网格量约2543 万.计算马赫数为3，单位长度雷诺数为3.67 × 107m-1，攻角为0°.图9 给出了典型截面物面压力系数对比结果，其中D表示圆柱直径，θ表示圆柱轴向截面周向角度，计算结果表明，CFD 计算结果与文献[30]中给出的数值仿真结果和风洞试验数据吻合良好.此外图10 给出的计算云图和风洞试验纹影图高度一致，能够准确的捕捉到流场中主要波系结构.

图8 激波边界层构型结构网格示意图Fig.8 Illustration of structure grid of shock-wave boundary-layer interactions

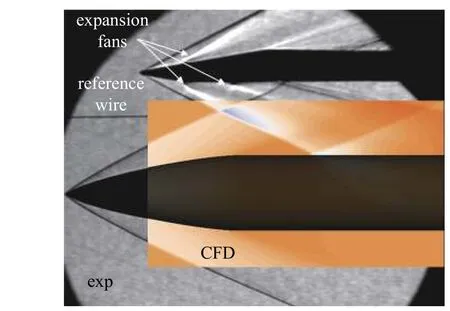
图10 CFD 结果与风洞试验对比Fig.10 Comparison of CFD with wind tunnel test

综上所述，本文采用的CFD 数值方法具有较高的可信度.

采用上述数值方法对圆锥-圆台体组合捕获翼概念构型进行求解，图11 为计算构型结构网格示意图，近壁面边界层区域网格进行加密，总网格量约为2900 万，壁面法向第一层网格厚度为L(× 10-5m)，其中L是机体总长度1.5 m.选取马赫0.3 至3 范围内的典型状态点进行计算，来流马赫数分别为0.3，0.5，0.7，0.92，1.1，1.3，1.5，2 和3，来流单位长度雷诺数均取为1.334 × 107m-1，计算攻角均为0°.

图11 计算构型结构网格示意图Fig.11 Illustration of computational grid of calculation configuration

针对不同的来流马赫数，流场结构大致分为亚声速流场、跨声速流场和超声速流场.下面对不同来流马赫数下的流场结构分别进行分析与讨论，重点关注捕获翼与机体之间的气动干扰以及捕获翼下表面与机体上表面的物面压力变化规律.

3 亚声速条件下流动特性分析

3.1 流场结构分析

当Ma＜0.7 时，流场中最大马赫数小于1，整个流场为亚声速流动.图12 给出了Ma=0.3，0.5 和0.7来流条件下纵向对称面和轴向截面的马赫数等值线分布，来流受到机体圆锥段的压缩加速，靠近捕获翼前缘时，受到捕获翼前缘干扰而减速，随后进入机体与捕获翼之间的流场区域.经过圆锥-圆台交界点之前，因为机体与捕获翼之间垂向距离不断减小，来流受到压缩而加速，在垂向距离最小处附近马赫数达到最大值.通过圆锥-圆台交界点后，随着机体与捕获翼之间垂向距离增大，来流受到膨胀不断减速，直至达到机体尾部并且与外部流场相匹配.

图12 纵向对称面和圆台中点处轴向截面马赫数等值线分布图Fig.12 Contour of Mach number of symmetric plane and axial cross section

捕获翼的存在对圆台上表面附近的流动产生明显的干扰.图12 给出了x/L=0.833 处截面马赫数等值线图，由图可知Ma=0.3 时，机体附近的流场基本保持了二维轴对称流动特性，仅在机体上表面对称面附近受到捕获翼干扰，干扰区范围相对较小;Ma=0.5 时，二者之间的气动干扰增强，干扰区范围沿着垂向和展向发展扩大，并且主要集中在机体上表面;Ma=0.7 时，干扰区的范围进一步扩大，机体与捕获翼的流场逐渐耦合在一起，二者的气动干扰更加强烈.综上所述，随着来流马赫数的增大机体与捕获翼之间的气动干扰逐渐增强，干扰区范围逐渐扩大，导致圆台上表面分离区的出现和发展.

来流经过机体与捕获翼之间的流场先加速后减速，会导致来流压力先减小后增大，因此流场中机体尾端出口处压力高于上游圆锥-圆台交界点处的压力，机体上表面尾部出口处与圆锥-圆台交界点之间存在逆压梯度，并且随着来流马赫数的增大逆压梯度增大，机体圆台段上表面附近出现流动分离现象.图13中给出了机体尾段不同位置轴向截面的流线分布，如图所示Ma=0.3 时，机体轴向截面流线分布均近似于二维轴对称分布，捕获翼对机体干扰相对较弱，圆台附近流场没有分离现象;Ma=0.5 时，圆台上表面分离区开始出现，圆台上表面左右两侧各产生一个分离涡，并且沿流向涡核逐渐向对称面附近运动，同时沿垂向发展逐渐脱离机体上表面;Ma=0.7 时，分离涡产生的位置更加远离对称面，由于逆压梯度的增大，在相同截面下分离涡范围扩大，涡核的运动规律与Ma=0.5 情况类似.

图13 轴向不同位置流线分布Fig.13 Streamline distribute at different axial cross section

3.2 物面压力分布

图14 分别给出了机体上表面和捕获翼下表面不同展向位置压力系数Cp分布曲线，图中横坐标给定的范围为高压捕获翼的前缘至后缘，下同.由图可知，由于机体与捕获翼之间流场对来流的压缩-扩张作用，捕获翼下表面与机体上表面压力系数沿流向均先减小后增大，在机体圆锥-圆台交界点附近达到极小值.

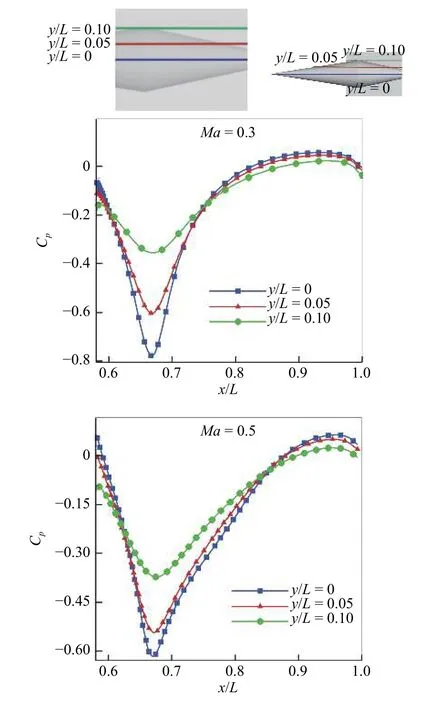
图14 捕获翼下表面和机体上表面Cp 分布曲线Fig.14 Curve of Cp at different spans of HCW lower surface and fuselage upper surface

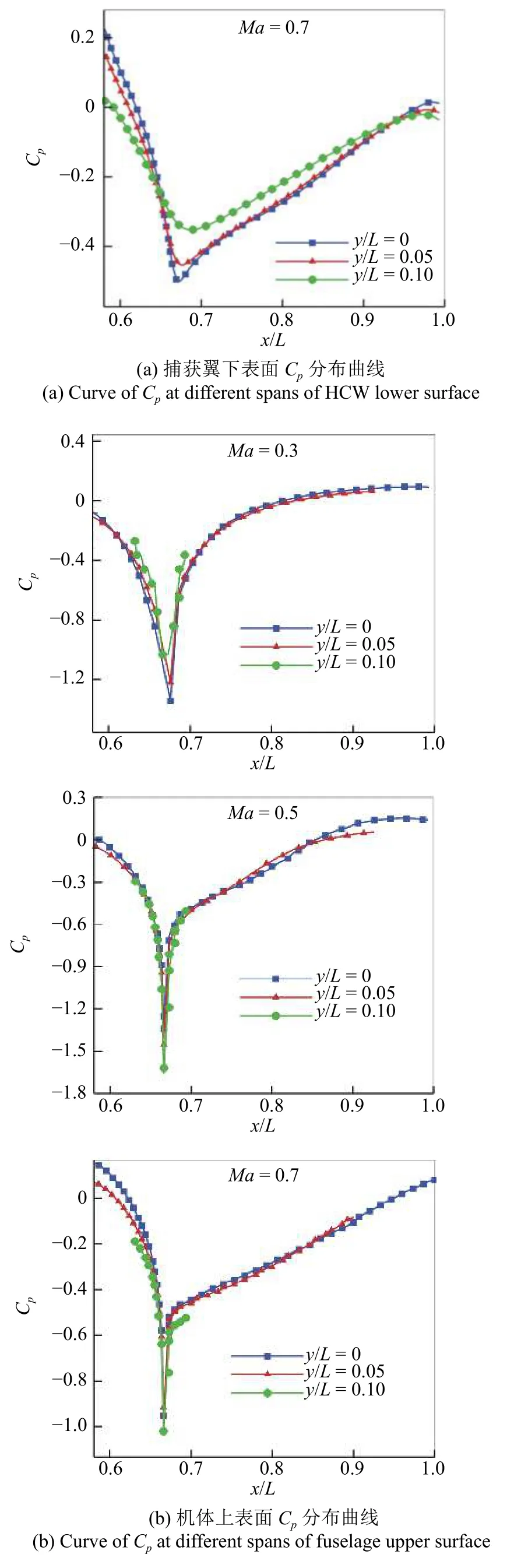
图14 捕获翼下表面和机体上表面Cp 分布曲线 (续)Fig.14 Curve of Cp at different spans of HCW lower surface and fuselage upper surface (continued)

捕获翼下表面压力系数分布具有明显的三维效应，具体表现为沿展向位置机体与捕获翼之间垂向距离增大，二者之间的气动干扰逐渐减弱，捕获翼下表面压力系数最小值逐渐增大.随着马赫数的增大，机体与捕获翼之间的气动干扰逐渐增强，机体与捕获翼之间的干扰区沿展向扩大，捕获翼下表面不同展向截面物面压力曲线逐渐趋于一致.

圆台上表面物面压力分布与捕获翼下表面分布规律相似，即沿流向先减小后增大，但由于圆台段受到分离区的影响，机体拐点处压力系数极小值沿展向的变化规律略有不同.具体表现为，Ma=0.3 时流场中无分离现象，圆台上表面干扰区主要集中在对称面附近，因此不同截面压力系数极小值沿展向逐渐回升;Ma=0.5 与0.7 时，由于圆台上表面出现流动分离现象，不同展向截面处压力系数分布趋于一致，但由于分离涡产生的位置在机体两侧，受此影响远离对称面的x/L=0.10 截面的压力系数极小值与两外两个截面相比要更小.

4 跨声速条件下流动特性分析

4.1 流场结构分析

来流马赫数继续增大，流场中开始出现激波逐渐演化为跨声速流场，图15 依次给出了Ma=0.92，1.1，1.3 和1.5 条件下纵向对称面和轴向截面马赫数等值线分布图.Ma=0.92 时，来流经过机体前段的压缩开始加速，随后进入到机体与捕获翼之间的流场区域，在达到机体圆锥-圆台分界点之前一直加速，在机体拐点附近马赫数达到1，当来流经过机体拐点后受到扩张段的膨胀作用继续加速直至产生激波，激波与圆台上表面的分离区相互作用，使分离区范围增大，并且在激波后产生若干的二次激波[30];Ma=1.1，1.3 和1.5 时，来流经过机体圆锥段和捕获翼前缘产生的两道弱激波作用后减速至亚声速流动，随后进入到捕获翼与机体之间的流场区域，来流在到达机体圆锥-圆台分界点之前再次加速至声速，经过分界点之后受到膨胀继续加速直至产生激波.

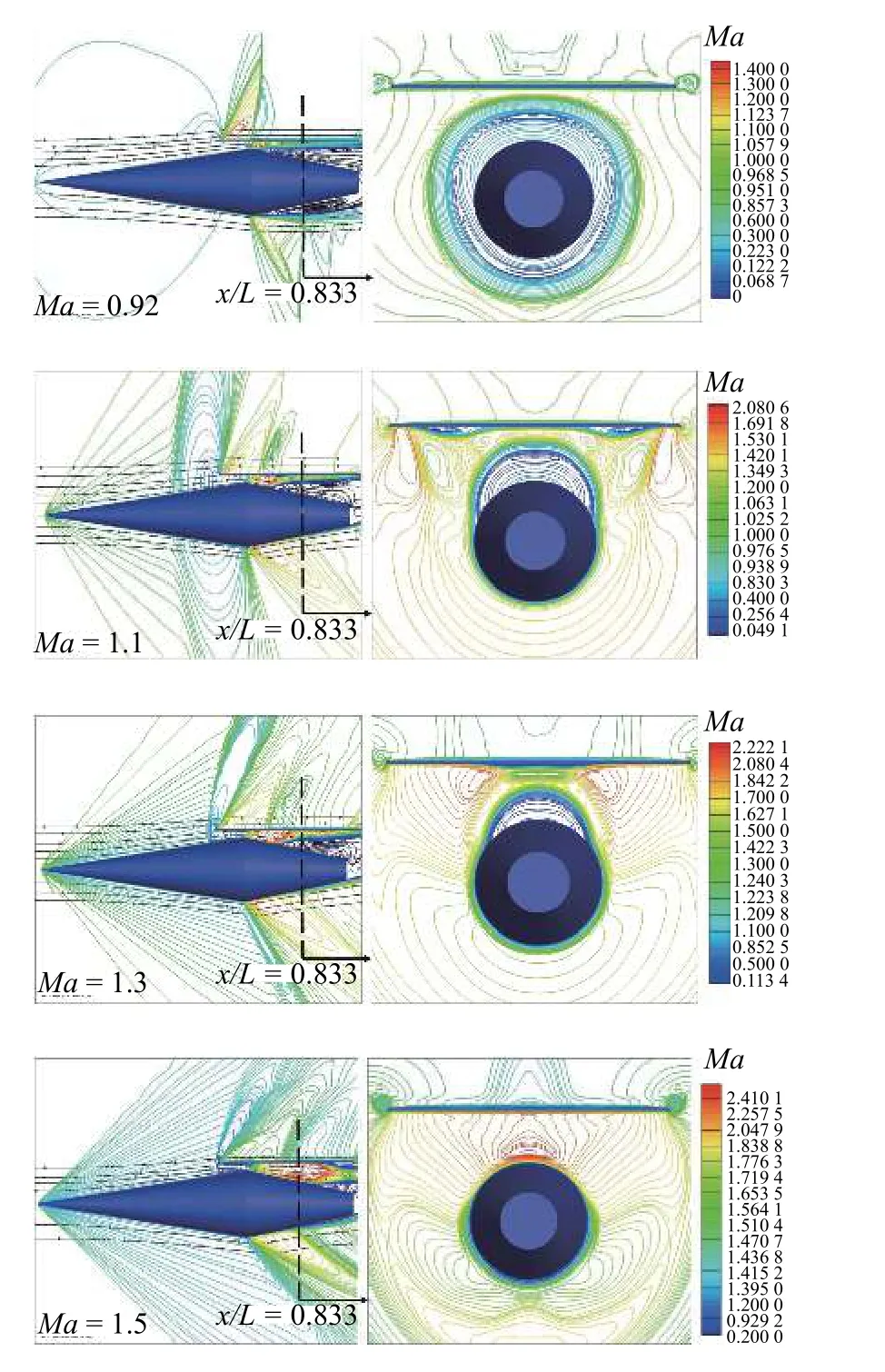
图15 纵向对称面和圆台中点处轴向截面马赫数等值线分布图Fig.15 Contour of Mach number of symmetric plane and axial cross section

激波的出现并且与分离区相互作用使得机体与捕获翼之间的流场结构变的更加复杂，也加剧了机体与捕获翼之间的气动干扰强度，由图15 中给出的x/L=0.833 处轴向截面马赫数分布等值线图可知，受到激波的干扰，Ma=0.92 时机体上下表面均出现了流动分离现象，此时圆台上下表面的分离区相互连通，分离区的范围进一步增大;Ma=1.1，1.3 和1.5时，马赫数的增大通道内超声速区域逐渐扩大激波出现的位置后移，激波后的分离区范围逐渐缩小，由马赫数等值线图可知，机体与捕获翼之间的干扰区主要集中在机体与捕获翼之间开放通道对称面附近.

由上述分析可知，跨声速来流下机体与捕获翼之间流场内激波出现的位置及其空间分布直接影响激波后的流场结构，尤其是分离区的范围和主激波后的二次激波位置.图16(a)给出了3 组Ma=0.92 来流条件下不同展向截面高压捕获翼附近的马赫数分布，由于捕获翼的影响，机体尾部分离区范围上表面相较于下表面明显增大，由此导致高压捕获翼和机体之间一直呈现出等效的收缩形状.在跨声速来流条件下，收缩通道内出现了激波串现象，进而形成了多个超声速区和亚声速区[30].

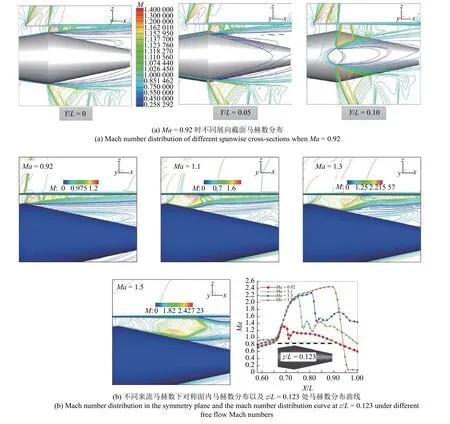
图16 机体与捕获翼之间流场内的马赫数分布Fig.16 Contour of Mach number between fuselage and HCW

图16(b)中给出了不同来流马赫数下机体与捕获翼之间流场区域对称面内马赫数分布，随着来流马赫数的增大，机体与捕获翼之间超声速区域范围增大，激波出现的位置逐渐后移，激波后分离区的范围相应减小.同时由对称面内z/L=0.123 处马赫数分布曲线可知，随着来流马赫数的增大，激波强度增强、激波首次出现位置后移并且二次激波现象逐渐消失.

4.2 物面压力分布

图17 给出了捕获翼下表面和机体上表面不同展向截面位置的压力系数分布曲线，受到激波及其诱导的二次激波影响，Ma=0.92 和1.1 时捕获翼下表面出现明显的压力波动现象;Ma=1.3 时，超声速区域扩大，激波位置后移二次激波现象基本消失，压力波动现象逐渐减弱;Ma=1.5 时捕获翼前缘激波反射导致前缘下表面附近产生高压区，随后来流不断加速导致捕获翼下表面压力逐渐减小，在靠近机体尾部受到激波作用导致压力有小幅增大.另外沿展向发展可知，跨声速流动状态下激波位置逐渐后移且二次激波现象逐渐消失，压力波动现象逐渐减弱.

图17 捕获翼下表面和机体上表面不同展向位置Cp 分布曲线Fig.17 Curve of Cp at different spans of HCW lower surface and fuselage upper surface

图17 捕获翼下表面和机体上表面不同展向位置Cp 分布曲线 (续)Fig.17 Curve of Cp at different spans of HCW lower surface and fuselage upper surface (continued)

机体上表面由于受到分离区的影响压力系数变化较为平缓，Ma=0.92 时，来流经过捕获翼与圆锥之间的收缩通道时受到压缩的作用，来流速度增大，物面压力逐渐减小，在拐点附近来流加速至声速，同时由于机体的转折形成膨胀波，受其作用来流速度迅速增加，导致物面压力急剧减小，随后在圆台上表面回流区的作用下流速逐渐减小，物面压力逐渐回升[30];Ma=1.1 时，机体与捕获翼之间的超声速区域范围逐渐增大，激波位置后移，因此在机体交界点和激波位置之间产生了一个低压区间，经过激波的作用压力剧增，随后在分离区的影响下压力缓慢增大;Ma=1.3 时，物面压力变化规律与Ma=1.1 大体一致，机体与捕获翼之间的区域内超声速范围进一步扩大，激波出现的位置更加靠后，因此低压区间范围更大，随后经过激波的作用压力增大，最后在分离区的影响下压力逐渐回升;Ma=1.5 时，捕获翼前缘激波打在机体上表面导致机体上表面物面压力有明显的升高现象，随后来流不断加速，机体物面压力逐渐减小，直至机体尾段产生激波，受到激波作用物面压力有小幅的增大.

5 超声速条件下流动特性分析

5.1 流场结构分析

随着来流马赫数继续增大，整个流场呈现以激波为主导的结构形式，图18 中给出了Ma=2 和3 来流下的纵向对称面和轴向截面马赫数等值线分布图.如图所示，Ma=2 时来流经过机体激波和捕获翼前缘激波减速后，进入到机体与捕获翼之间的通道内，随后经过机体拐点处的膨胀波加速直至机体尾部，Ma=3 情况与之类似.

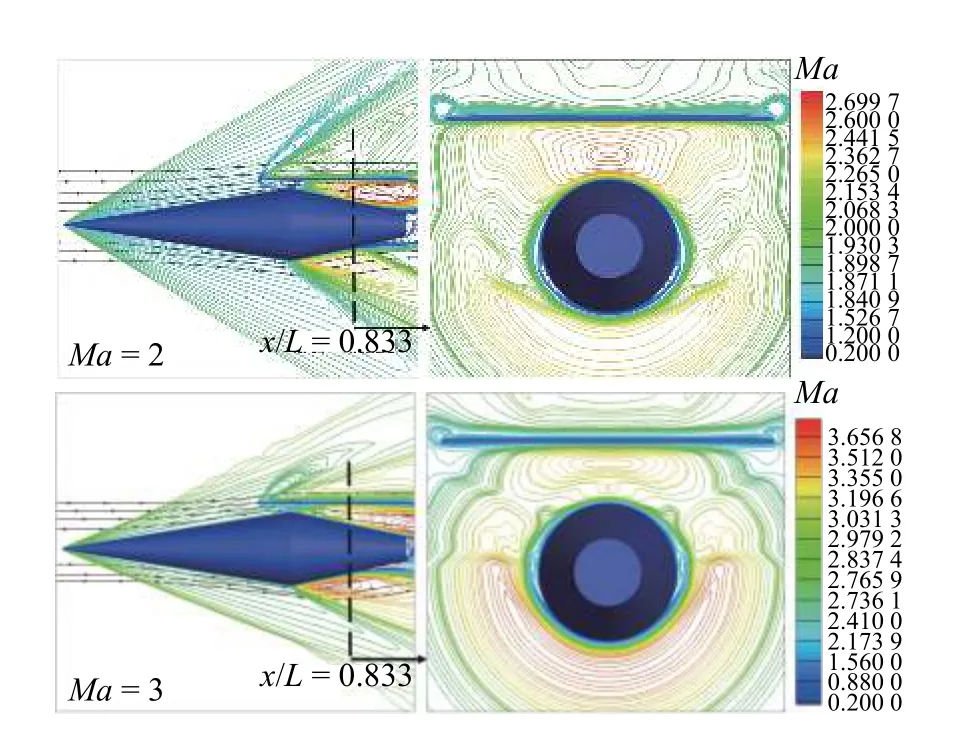
图18 纵向对称面和圆台中点处轴向截面马赫数等值线分布图Fig.18 Contour of Mach number of symmetric plane and axial cross section

机体与捕获翼之间的通道内气动干扰仍然主要存在机体上表面附近，图18 中给出了x/L=0.833 处轴向截面马赫数分布图，超声速来流条件下，由于捕获翼的存在限制了机体上表面来流的膨胀，进而使机体上表面产生的激波位置较机体下表面更加靠后，而且捕获翼对机体上表面来流膨胀的限制在对称面附近最为强烈，沿展向发展这种限制作用逐渐减弱.

超声速来流条件下，捕获翼前缘会产生弓形激波，激波会作用在机体压缩段上表面，导致捕获翼前缘与机体附近流场产生激波边界层干扰和机体反射等现象.如图19 所示，Ma=2 时，捕获翼前缘激波S1 打在机体上表面，反射激波S2 打在捕获翼下表面，随后反射激波S3 作用在机体拐点附近，S3 的反射激波受到机体拐点附近的膨胀波E1 作用而弱化消失.Ma=3 时捕获翼前缘激波S1 强度增大，S1 打在机体上表面后反射激波S2 作用在捕获翼下表面，随后反射激波S3 穿过机体拐点膨胀波E1 打在机体上表面，最后反射激波S4 打到通道外.

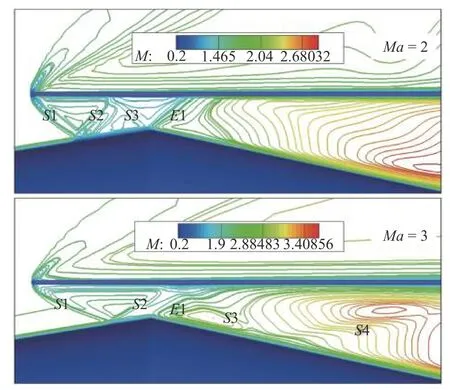
图19 捕获翼前缘与机体上表面附近的激波干扰波系结构Fig.19 Shock interference between the leading edge of HCW and fuselage upper surface

5.2 物面压力分布

图20 给出了Ma=2 和3 捕获翼下表面和机体上表面压力系数分布曲线，Ma=2 时捕获翼前缘激波经过机体反射重新作用在捕获翼下表面，捕获翼下表面在拐点前压力会出现明显增大现象，随后经过机体拐点来流受到膨胀加速，捕获翼下表面压力逐渐减小，而且膨胀段已经没有明显的激波现象;Ma=3 时与Ma=2 情况类似，但激波反射点更靠后，导致压力峰值也更加靠后.分别是此外不同展向位置压力系数分布也说明了捕获翼前缘激波面的三维效应，沿展向激波强度逐渐减弱且出现的位置逐渐后移.

图20 捕获翼下表面和机体上表面不同展向位置Cp 分布曲线Fig.20 Curve of Cp at different spans of HCW lower surface and fuselage upper surface

图20 捕获翼下表面和机体上表面不同展向位置Cp 分布曲线 (续)Fig.20 Curve of Cp at different spans of HCW lower surface and fuselage upper surface (continued)

捕获翼前缘激波作用在机体上表面也会对其物面压力分布产生显著影响，由图20 可知Ma=2 时，捕获翼前缘激波增强，机体上表面受此干扰物面压力急剧增大，随后经过机体拐点，来流受到膨胀，物面压力持续减小直至机体尾部;Ma=3 时机体上表面会有两个压力峰值，分别是两次激波反射导致的.

6 气动力特性分析

为分析圆锥-圆台组合平板构型在宽速域内的气动力特性，图21 给出了升力系数(Cl)、阻力系数(Cd)和俯仰力矩系数(Cmy)随马赫数(Ma)变化曲线，其中参考面积为整机俯视投影面积0.318 m2，参考长度为整机全长1.5 m，力矩参考点选在原点即机体前缘点.图中all 代表整机，HCW 代表高压捕获翼部件，body 代表圆锥-圆台机体.

如图21 所示，在宽速域内整机的阻力系数主要由机体提供，由于在0°攻角下捕获翼与来流方向平行，捕获翼的阻力系数相对较小.随来流马赫数增加，整机阻力系数先增大后减小，在Ma=1.1 附近达到最大值.当Ma＜1.1 时，随来流马赫数增大机体与捕获翼之间的通道内会逐渐出现流动分离且分离区范围逐渐扩大，整机阻力系数随之增大;当Ma＞1.1 后，随马赫数增大通道内激波出现的位置逐渐后移，分离区的范围逐渐缩小直至消失，整机阻力系数随之减小.

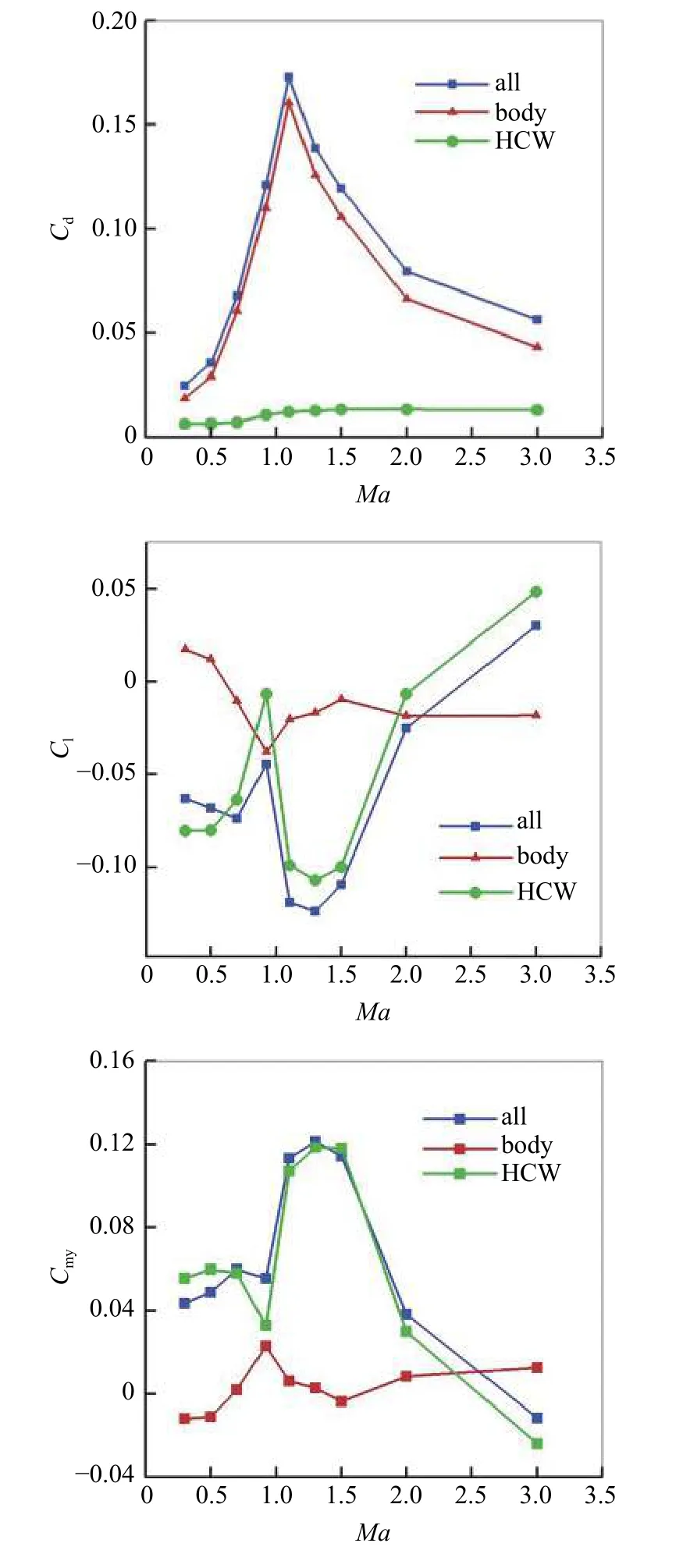
图21 气动力参数随马赫数变化曲线Fig.21 Variation of aerodynamic parameters with Mach number

整机升力系数主要由捕获翼提供，机体贡献的升力系数占比较小，由于当前计算状态仅考虑了0°攻角，因此在亚跨超来流条件下整机基本处于负升力状态.当Ma=0.3 至0.7 时，整机升力系数随马赫数增大逐渐减小，这是由于机体与捕获翼之间通道内逐渐出现分离区并且范围逐渐增大，分离区的出现会导致捕获翼下表面附近的来流被压缩加速，进而使捕获翼下表面产生的低压区范围逐渐增大，导致升力系数逐渐减小;Ma=0.92 至1.3 时，整机的升力系数会急剧减小，这主要是因为通道内激波位置逐渐后移，通道内激波前的超声速区域产生的低压范围逐渐扩大，同时捕获翼上表面也会出现激波，使得整机产生的升力急剧减小;Ma＞1.3 之后，捕获翼前缘激波打在机体上并且发生反射，反射激波会作用在捕获翼下表面进而产生额外的升力，此时整机升力系数逐渐增大.

俯仰力矩系数受压力分布特性和升力系数影响，整机俯仰力矩系数主要由捕获翼提供，机体的贡献较小.由于整机升力主要由捕获翼提供，且捕获翼相对力矩参考点距离较大，因此整机俯仰力矩系数随马赫数变化规律基本与升力系数变化规律呈镜像对称.

7 结论和展望

本文基于一种圆锥-圆台组合平板原理性构型，重点关注机体与捕获翼之间的气动干扰，对高压捕获翼新型气动布局在亚跨超速域下的典型流动特性进行了研究.结果表明，二者之间的气动干扰存在明显的三维效应，从对称面向展向逐渐减弱，其流动特性随马赫数的增加发生明显改变，具体如下:

(1)亚声速来流在经过机体与捕获翼之间通道时先加速后减速，产生逆压梯度.在Ma=0.5 时开始出现分离，且分离区随马赫数的增加而逐渐向展向扩展;

(2)跨声速来流在机体拐点膨胀波的作用下沿流向加速至超声速，随后受到分离区的影响产生激波以及二次激波，在捕获翼下表面产生明显的压力波动.随着马赫数的增加，激波后移，分离区缩小;当Ma=1.5 时，二次激波基本消失，分离区退至机体尾部;

(3)超声速来流时，捕获翼前缘激波在通道内发生多次正规反射，并与机体拐点膨胀波相互干扰.受来流马赫数的影响，呈现不同的波系结构.

总体来看，捕获翼与机体之间在不同速域下呈现出明显不同的典型流场结构.在亚声速时，有分离区产生;跨声速时，出现了激波-分离区干扰结构;超声速时，以激波-膨胀波波系干扰为主.上述流场结构均会对气动力特性产生显著影响，在宽速域来流条件下，整机阻力系数主要由机体贡献，并且随马赫数先增大后减小;整机升力系数与俯仰力矩系数主要由捕获翼贡献.

为初步摸清高压捕获翼布局在亚跨超条件下的流动特性，本文仅对简化原理构型定攻角状态进行了分析，暂未考虑下翼面、外形优化以及攻角的影响.下一步拟在本文研究基础上，重点考虑在亚声速时如何有效抑制分离、在跨声速时如何改善激波-分离干扰、以及在超声速时如何优化波系结构等问题，综合考虑气动力和力矩特性，开展构型设计与优化，进一步探究相关流动特性和机理.