低年级运算教学中渗透运算能力的培养——以一上《8、7加几》一课的教学为例

孙云卓

《8、7加几》是苏教版一上的教学内容，它是在学生学过“9加几”之后进行教学的，是培养学生数学思维能力的重要一课。笔者认为，在教学中，教师不仅要让儿童把握运算的结构模型，还要让他们经历运算的推理过程，初步培养其运算能力。

一、推动儿童把握运算的结构模型

运算作为数学学科的子系统，蕴含着诸多数学关系，具有很强的结构性和关联性。低年级的运算学习，就应该蕴含着结构思维与模型思想。教学时，教师应注意根据运算之间的本质关系和学生的认知经验储备，从纷繁复杂的关系中精心识别、选择运算关系，作为运算推理的引擎，让运算的结构锚桩从小就在学生心里埋下模型。

1.在数与事的关系中引入生活原型。

今天，喜羊羊给大家带来了2个宝箱，里面藏着什么呢？想知道吗？你要闯过关卡，才能拿到钥匙。（课件出示钥匙）

第一关：9+2、9+5、9+7、9+9，这些都是9加几的算式。那9+7你是怎么计算的？我们在计算“9加几”时都用到了这样的“凑十法”，请你再说一题给同桌听。

打开第一个宝箱，里面有什么呀？（出示8个喇叭，让学生数一数）

第二关：三个气球上的数字合起来是多少？请你迅速计算出结果。（4、2、8；7、8、3；9、1、8；3、9、7）

你们怎么这么快就算出来了?（先想办法凑成10，再用10加几）

恭喜你们闯过第二关，打开第二个宝箱，（出示7个喇叭）里面是什么呀？（再次出示8个喇叭）你想问什么问题呢？

数学运算与生活事件之间有着流与源的关系。上述教学，教师精选儿童熟悉而又喜欢的生活原型，让他们自主探究，积累数学活动经验，为其理解数学算理提供坚实而鲜活的事理依据。

2.根据数与数的关系建构分合模型。

师：小朋友们太厉害了，喜羊羊要继续考考大家，看！（出示7+9）

师：你会算吗？想一想，自己写一写。

（1）出示图1。

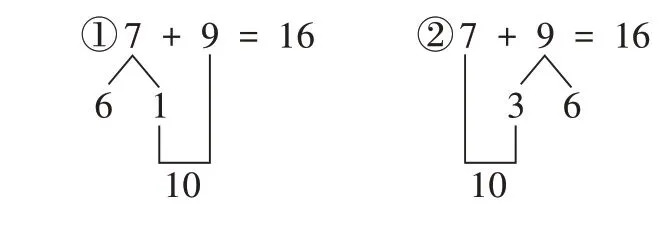
（图1）

师：你能看懂吗？你是怎么想的？

师：仔细看一看这两种方法，你更喜欢哪一种？能说说为什么吗？

师：老师看到大多数小朋友都习惯把大数凑成10，把小数拆一拆，这叫作“凑大数，拆小数”。

（2）出示：9+7=16；7+9=16。

师：还有小朋友是这样做的，你能看懂吗？是怎么想的？是呀！可以用“好朋友”的方法。

无论是“9加几”还是“8、7加几”，内在都有着“凑十法”这一数理模型。对“8、7加几”而言，“9加几”就是源，数与数之间的关联是数学学科最本质的关系。教师应跳出课时教材内容编排的束缚，沿着运算知识的发展脉络寻求运算的关系“源”，让运算推理活动成为有源之水。

二、让儿童经历运算的推理过程

在数学运算中，算理理解、算法运用、问题解决等其实都是运算关系再推理的思维过程。运算教学不仅要让学生掌握算法、理解算理、合理简算，还要注意培养其数学推理能力。

1.从多样到优化，让儿童经历比较与分析。

师（出示图2）：看了图，你能提出什么数学问题？

（图2）

生：一共有多少把小号?

师：8+7可以怎样算呢?请大家用小棒摆一摆，并说说你是怎样算的。

生操作探究后全班交流。

生1：我先把8根凑成10，再加上5就是15根。

生2：我先把7根凑成10，再加上5就是15根。

生3：我是想9+7=16，所以8+7=15。

生4：我先把左边看成10，10+7=17，17-2=15。

师：大家想出了这么多种方法来计算8+7，你比较喜欢哪种方法呢?用你喜欢的方法计算7+9，说说你是怎样想的，比较不同的方法，你想说什么?

教师没有急于指出“凑十法”的优越性，而是让学生自己动手操作探究，培养他们的探究能力。学生通过摆小棒、画圈、摆圆片等方式，逐步体会到计算“8加几”时，可以先借2个与8凑十，然后计算10加几是十几；也体会到了“7加几”的特点，可以先借3个与7凑十，然后计算10加几是十几。

2.从个到群，让儿童学会类比与迁移。

师：今天，你学到了什么?

生：用“凑十法”计算“8、7加几”。

师：见8想几凑成10？见7想几凑成10？

…………

师：今天学习的“8、7加几”与上节课学习的“9加几”相比，有什么相同的地方？用这样的方法还可以学习哪些加法的计算呢？

通过对比“8、7加几”与“9加几”，教师引导学生掌握“凑十法”，并优化算法；一般情况下看大数、分小数，得出相似模块与结构模型，并以此类比同化，迁移到其他加法的学习中。

运算能力是儿童数学学习中的关键能力之一。教师在低年级运算启蒙学习中播下运算的良种，将有助于儿童数学运算能力的生长。