基于地震波频谱分析与线性叠加的电子雷管延时优选

何 理 谢先启 韩传伟 钟冬望 王洪刚 黄小武 黄炳林

（1.武汉科技大学冶金工业过程系统科学湖北省重点实验室，湖北 武汉 430065；2.爆破工程湖北省重点实验室，湖北 武汉 430056；3.武汉爆破有限公司，湖北 武汉 430056）

钻爆法施工是现今最为经济、高效的破岩手段之一，被广泛应用于交通隧道建设、矿产资源开采与水利水电工程建设中。研究和应用实践均表明，使用电子雷管精确延时可以降低爆破振动，改善爆破效果，在城镇爆破开挖及隧道爆破掘进中优势明显［1-3］。钟冬望等［4-5］研究指出，电子雷管合理延期时间往往是一个或多个时间区间，并且随着爆心距的变化合理延期时间并非定值。傅洪贤等［6］结合隧道穿孔爆破实践给出了不同隧道围岩级别情况下掏槽孔、周边孔及辅助孔的建议延期时间。田振农等［7］采用时—频分析揭示了隧道爆破振动的一般特征，提出了电子雷管错相减震机理。李清等［8］结合隧道爆破实践，研究指出延期时间应不小于新自由面形成所需要的时间。凌同华等［9］基于小波变换从实测微差爆破振动信号中分离出分段振波，通过不同延期时间叠加各分段振波达到优选孔间延期时间的目的。赵明生等［10］、杨年华等［11］基于实测单段波形线性叠加分析，优选孔间延期时间，实现了地震波的干扰相消。然而迄今为止，对孔间延期时间的设置尚未形成统一的认识，各种延期时间的优选方法普适性均有所不足，施工现场更多依赖经验和多次试验来确定电子雷管延期时间［12-13］。并且，往往爆区待保护对象有多个，但是电子雷管延期时间设置需要考虑爆心距因素，现有研究成果多是针对特定建（构）筑物提出，因此，亟需解决不同爆心距处被保护对象延期时间的优选问题。

结合国内某红砂岩石方开挖爆破工程，本研究设计开展电子雷管爆破振动监测试验，通过频谱分析讨论地震波主振频率演变规律；基于地震波线性叠加原理，运用MATLAB编制计算程序，研究叠加波列数与孔间延期时间对合成波形峰值振动速度的影响机制，建立电子雷管延期时间的确定方法。研究成果可为城市复杂环境下岩石开挖爆破电子雷管延期时间设置提供参考。

1 爆破振动测试试验与分析

1.1 场地概况

爆破振动测试试验在国内某红砂岩石方开挖爆破工程一平整场地进行，由于该工程部分工作面紧邻村庄、学校等建（构）筑物，因此需要重点关注爆破有害效应，尤其是实现爆破振动的精细控制极为必要。试验前，在工程现场钻孔取芯选用密实均匀和完整性良好的红砂岩制备试件，按照岩石力学的试验测试要求，试件尺寸为50 mm×50 mm（直径×高度），并且对试样端面进行打磨，确保端面法线偏差小于0.25°，试样端面不平整度小于0.02 mm。室内试验测得红砂岩试件的密度为2.55 g/cm3，纵波波速为2 121 m/s，单轴抗压强度为60 MPa。

1.2 爆破参数与测振方案

根据实际生产爆破情况，单孔爆破试验时垂直下向钻孔，选用连续装药结构，通过单发电子雷管孔底反向起爆。炮孔直径为90 mm，炮孔深度为2.5 m，单孔装药量4 kg，堵塞长度为1.5 m。炮孔装药结构如图1所示。

为获取可真实反映红砂岩地质条件属性的单孔爆破振动信号，选取较为平齐、完整的工程区域范围，在爆心距分别为10、15、20、25 m处共布置了4个振动监测点，每个振动监测点放置2台振动测试仪器，且4个振动监测点均布置在同一条测线上，目的是尽可能减小传播路径差异（传播介质属性）对振动测试波形的影响。试验完成后分别相互对比分析4个振动监测点处2台振动测试仪的监测指标（峰值振动速度、振动持续时间、振动主频），如果任一指标间的相对误差超过5%，则重复进行爆破振动监测试验，直到监测指标趋于稳定。

1.3 测试结果与分析

试验测得的单孔爆破振动波形如图2所示。

由于爆破试验在平整场地开展，无需考虑高程差因素对爆破振动传播的影响，故选取如下形式的PPV预测模型：

式中，PPV为质点峰值振动速度，cm/s；R为爆心距，m；Q为最大单响药量，kg；k、α是场地条件相关系数，与爆破方式、装药结构、爆破点至监测点间的地形、地质条件密切相关［14］；SD为比例距离［15］，m/kg1/3。

同时，利用MATLAB编制计算程序，对振动信号进行频谱分析，得到不同爆心距处振动信号的主振频率，如图3所示。

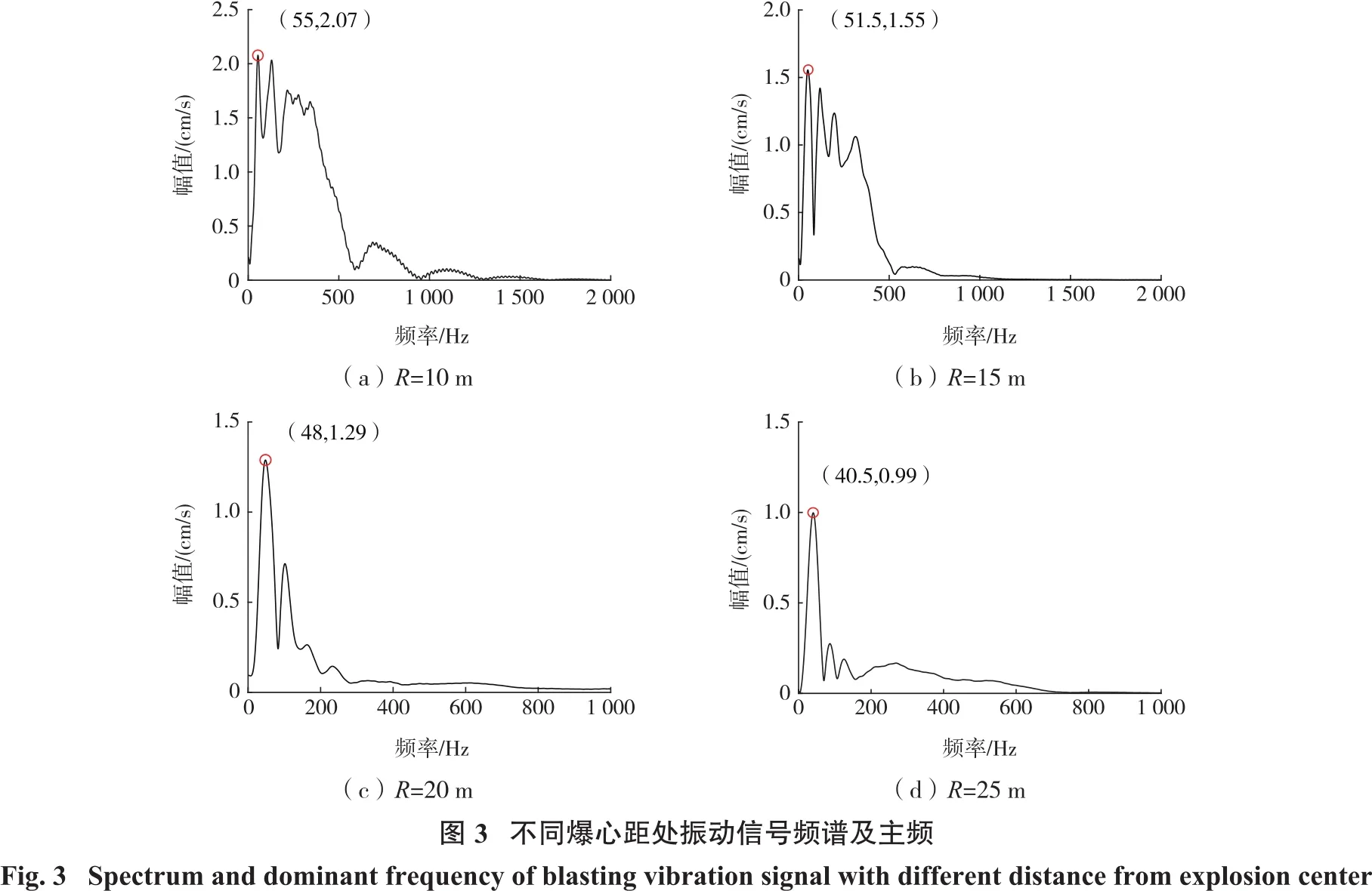
爆破地震波峰值振动速度PPV与振动主频F随比例距离的变化关系如图4所示。

根据图4，可拟合得到红砂岩场地爆破振动速度的预测模型为

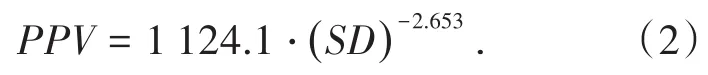
数据拟合相关系数达到0.951 4，表明该模型回归拟合效果良好，式（2）中的场地条件相关系数可真实表征施工现场的地质条件属性。

并且，可得到爆破振动主频随比例距离增加近似呈幂函数形式衰减，振动主频F衰减公式为

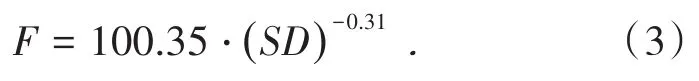
2 单孔爆破振动曲线拟合及其线性叠加原理

单孔爆破获得的不同爆心距处爆破地震波形中包含了爆源到振动监测点传播介质的地质属性。假设单孔爆破地震波形是由无数个正弦谐波组成，谐波间相互干扰叠加，正、正相位间波形幅值叠加相长，致使地震波幅值增加，正、负相位间波形幅值干扰相消，致使地震波幅值降低［16-19］。群孔爆破地震波可视为由特定数目的单孔地震波形线性叠加组成［20］，叠加方法如下式：

式中，V(t)为线性叠加原理预测得到的群孔爆破地震波形；t为时间；n为爆破地震波列数；vi(t)为单孔爆破地震波形；i为地震波形段号，i=1,2,3,…,n；Δt为段间延期时间。

利用MATLAB编程计算程序，基于Fourier级数拟合得到单孔地震波形的拟合函数ϕ(t)［21］，函数形式为

式中，ϕ(t) 为单孔地震波形拟合函数；a0、aj、bj为Fourier拟合系数；ω为基频；l为Fourier拟合级数。

式（5）中，a0、aj、bj以及基频ω的计算公式为

式中，T为波形截断时间；M为总采样点数；ym为第m个采样值。

将拟合函数ϕ()t扩展至时间全域，得到最终单孔地震波形函数v()t为

3 波列数与延期时间对合成波形峰值振动速度的影响机制

3.1 波列数对合成波形峰值振动速度的影响规律

生产爆破实践中，现场实测波形往往是多个炮孔爆炸后各波形的叠加结果。假设每段产生的单孔波形相同，当段数不同时，相同延期时间下合成（叠加）波形的峰值振动速度也可能存在差异［17］。因此，利用地震波线性叠加法分析延期时间和合成波形峰值振动速度间的关系时，首先消除叠加波列数对合成波形峰值振动速度的影响极为必要。本研究基于地震波线性叠加原理，利用MATLAB编制计算程序，叠加波列数取为n∈[ ]2,40，且为整数；各波列间延期时间取为Δt∈[ ]1,80ms，且为整数。

以图2中10 m监测点处单孔地震波形为例，当叠加波列数为25时，合成波形峰值振动速度随延期时间的变化关系如图5所示。

根据图5可知，单孔爆破地震波形在一定波列数叠加情况下，不同延期时间叠加产生的合成波形具有不同的峰值振动速度。延期时间为1 ms或2 ms时，合成波形峰值振动速度小于单孔振波峰值振动速度；当延期时间超过特定值后，合成波形的峰值振动速度逐渐趋近并最终等于单孔爆破峰值振动速度。合成波形的峰值振动速度最小值与最大值分别出现在延期时间Δt=1 ms和Δt=19 ms时，此时的合成波形如图6所示。

通过前述分析计算方法，依次计算并统计出任意延期时间下合成波形的峰值振动速度最大值及最小值，得到合成波形峰值振动速度随波列数的变化关系，如图7所示。

依据图7可以得到，延时1～80 ms范围内，各监测点合成波形峰值振动速度最大值随波列数增加，呈现出先增大后减小，并最终趋于稳定值的变化规律。对于合成波形峰值振动速度的最小值，除了10 m爆心距处出现最小值随波列数上下波动，而后逐渐趋近单孔振波峰值振动速度外，其它监测点处最小值始终维持在单孔振波的峰值振动速度水平。进一步分析发现，最小值小于单孔振波峰值的情况仅仅出现在Δt=1 ms和Δt=2 ms处。然而在工程实践中，为取得良好的岩石破碎效果，通常设置段间延时不小于7 ms［16］，故本研究在分析波列数对合成波形峰值振动速度影响时，可忽略其对合成波形峰值振动速度最小值的影响。

根据图7统计出的合成波形峰值振动速度最大值趋于稳定的最小临界波列数，见表1。

?

由图7和表1可知：合成波形峰值振动速度最大值趋于稳定的临界波列数随监测点爆心距的增大逐渐增加，试验条件下当波列数n≥23时，在监测范围内可忽略其对合成波形峰值振动速度的影响，此时可仅考虑延期时间对合成波形峰值振动速度的影响。临界波列数随比例距离的变化关系如图8所示。

由图8可拟合得到合成波形峰值振动速度趋于稳定的临界波列数N的趋势线方程为

式中，N≥2且取整数。

利用式（8）可计算不同监测点处的临界波列数，研究结果可为红砂岩地质情况下，采用地震波线性叠加法预测爆破振动速度峰值及优选合理延期时间提供理论参考。

3.2 延期时间对合成波形峰值振动速度的影响规律

以15 m监测点处的单孔地震波形为例，以不同延期时间叠加23个波列，可得到合成波形峰值振动速度随延期时间的变化关系如图9所示。

由图9可知：针对露天台阶爆破工程实践，忽略段间延时小于7 ms的情况［16］，当孔间延时为12 ms时，合成波形峰值振动速度首次达到最小值3.739 cm/s；当孔间延时为9 ms和18 ms时，合成波形峰值振动速度达到较小值分别为4.027 cm/s、3.96 cm/s；当孔间延期时间为15 ms时，合成波形峰值振动速度达到最大值4.767 cm/s。

当孔间延期时间分别为12 ms和15 ms时，合成波形如图10所示。

由图10可知：当孔间延时为12 ms时，合成波形峰值振动速度出现在25.5 ms处，即第1和第2个波形产生了较弱的干扰叠加，峰值振动速度基本与单孔振波峰值振动速度相当，而后续波形产生了干扰相消。当孔间延期时间为15 ms时，合成波形峰值振动速度出现在28.5 ms处，表明第1和第2个波形产生了较强程度的干扰叠加，此时峰值振动速度达到单孔振波峰值的1.28倍，后期波形干扰叠加程度略微降低。

利用上述方法进行分析计算，依次统计出各监测点处合成波形峰值振动速度出现时刻，结果见表2。

?

由表2可知：各监测点处合成波形峰值振动速度最小值和较小值所对应的延期时间值多为相应测点单孔地震波形主振周期的0.4～0.6倍（0.5倍左右），说明通过设置合理的延期时间，利用电子雷管错相降振是可行的。然而，合成波形峰值振动速度最小值通常仅为单孔波形的峰值振动速度。当合成波形峰值振动速度出现最大值时，对应的延期时间值约为单孔振波主振周期的0.9～1.1倍（1倍左右），此时分段振波间存在振速叠加增强现象。

另外，当孔间延时达到主振周期约2.6倍以上时，合成波形峰值振动速度逐渐趋于稳定值（单孔振波峰值振动速度），各分段振波主震相之间的叠加干扰效应微乎其微，不会对合成波形峰值振动速度造成影响，工程实践中可借助这一原则对地震波主震相持续时间进行估算。进一步可得到确保合成波形峰值振动速度趋于稳定的主振周期倍数β随比例距离的变化关系如图11所示。

4 电子雷管延期时间优选方法

根据单孔爆破地震波形主振频率随比例距离的衰减公式，可以推导出孔间延期时间Δt的计算公式：

可以明确的是，当孔间延期时间为0.5倍的主振周期时，并不能完全确保合成波形峰值振动速度最小，只能说延期时间为主振周期的0.4～0.6倍时，合成波形峰值振动速度可能会出现最小值或较小值。然而，当延期时间为单孔振波主振周期的1倍左右时，合成波形必然会由于干扰叠加产生振速增强现象［17］。为了增强分段振波干扰降振的可靠性，使合成波形峰值振动速度尽可能降低，本研究提出了一种不同监测点处孔间最优延时确定方法，计算流程如图12所示。

计算步骤为：首先通过单孔爆破试验获取可表征现场地质条件与震动属性的单孔爆破地震波形，基于Fourier级数拟合得到单孔爆破地震波形的拟合函数v(t)，通过地震波线性叠加原理计算不同延期时间下的合成波形，从而初步选取孔间延期时间值Δt；然后，根据判断准则1（孔间延期时间Δt若满足确定该值为孔间最优延期时间Δt优；否则，根据判断准则2（孔间延期时间值Δt若满足确定该值为孔间最优延期时间Δt优。如果判断准则1和判断准则2均不满足，则返回前述步骤，直至得到孔间最优延期时间值Δt优为止。

5 结论

（1）试验研究得到合成波形峰值振动速度趋于稳定值的最小临界波列数N为23，并建立了临界波列数N的趋势线方程，其随比例距离近似呈对数形式增加，可为红砂岩地质情况下爆破振动速度峰值预测及合理延期时间优选提供理论依据。

（2）当孔间延时为主振周期的0.4～0.6倍时，合成波形峰值振动速度可能会出现最小值或较小值；当孔间延时为单孔振波主振周期的1倍左右时，合成波形必然会由于干扰叠加产生振速增强现象。当孔间延时达到单孔振波主振周期的2.6倍以上时，各分段振波主震相间叠加干扰效应减弱，合成波形峰值振动速度接近单孔爆破峰值振动速度，实践中可据此对地震波主震相持续时间进行估算。

（3）考虑爆心距因素对孔（段）间延时优选的影响，提出了一种不同监测点处孔（段）间最优延期时间确定方法，摆脱了传统方法仅能估算特定监测点处最优延时的限制，工程适用性更强。