基于分数倍内插的多相滤波器的设计与改进

魏汇赞,翟恒峰,王铭伟,杨自豪

（上海航天电子技术研究所，上海,201109）

0 引言

数字信号处理中，时钟域的转换非常常见，当两个时钟域完全异步时通常不可能通过整数倍的采样率变换来实现，只能通过分数倍采样来实现重采样[1-3]。实际大多数情况下重采样的采样率和原采样率相差非常小，因为采样率之间的差异主要是由于不同时钟源之间的频率误差造成的[4]。数字重采样的过程实际上可以看成是信号先通过一个零阶保持环节，回到模拟域，然后再根据新的采样时钟进行重新采样的过程。根据文献[5]可知，零阶保持过程会使原有信号产生一个镜像频率分量，这个镜像分量倍sinc函数加权，采样率越高这个分量越小。为了保证重采样后的误差足够小，这个分量必须抑制到足够小。因此针对不同的精度要求，在进行零阶保持之前必须将信号内插到足够大的采样率。

当重采样时钟频率和原采样时钟频率差别不大时，实际上零阶保持后的重采样过程可以看做是P/(P+1)倍或(P+1)/P倍的分数倍采样过程，其中P是一个非常大的正整数。实际上有的时候重采样时钟的与原采样时钟的比值并不一定严格等于P/(P+1)或者(P+1)/P，这时候可以通过不断改变采样倍数，如某些P/(P+1)倍重采样和P/P倍重采样相结合，平均采样率就可以达到介于P/(P+1)倍和1倍之间的某个倍数。而这种处理方式在P很大的时候所引入的误差是极小的。

1 分数倍内插多相滤波器的改进

由于内插和抽取只能应用于整数倍的速率变换系统中，具有一定的局限性。在实际的信号处理中，往往需要对信号的采样率进行分数倍变化，即传统的内抽和抽取就无法解决这个问题了。现假设需要对信号的采样率进行L/M倍变化，其中L、M都为整数。根据文献[6]可知，可以采用先对其进行L倍内插再通过M倍抽取的方式来实现；也可以通过先进行M倍抽取再进行L倍内插来实现。但是为了保证信号满足奈奎斯特采样定理，第二种方法具有一定的局限性。因此，目前的主流的实现方法如图1所示。先对输入信号进行L倍内插，再对信号进行M倍抽取，而中间的低通滤波器(low pass filter, LPF)为抗混叠滤波器。

图1 信号采样率的分数倍变换框图

在分数倍内插的实现中，低通滤波器的性能显得极为重要。其设计需要满足：(1)为了保证基带内的信号不失真，通带波纹要足够小；(2)为了有效滤除镜像成分，阻带衰减要足够小。

通过文献[7-8]可知，可以将低通滤波器的传递函数h(n)分成M相，且N为M的整数倍，即有

式(1)中，Ek(zM)为多相分量，其值为：

从上式(1)和式(2)中可以看出，可以将原滤波器分成M相不同的滤波器,且每一相滤波器的系数是通过对原滤波器系数的抽取获得的。其中第一组滤波器的系数为原滤波器系数的M整数倍的系数，第二组滤波器的系数为原滤波器系数的M整数倍加1的系数，以此类推。同理，当Q=N/L的时候，整数倍内插的多相滤波器的表达式为：

针对P/(P+1)倍内插而言，需要将滤波器分成P相，然后对每一相的输出数据进行选择；对于(P+1)/P倍内插而言，需要将滤波器分成(P+1)相，然后对每一相的输出数据进行选择。图2给出了现有内插滤波器的基本结构图。利用多相分解技术可知，原滤波器被分成了L个不同相，每相滤波器的阶数为原来的1/L。这样就使得原来复杂的滤波器结构得到了简化，简化了滤波器的实现。并且现在的卷积运算是在内插之前进行的，也就是在低采样速率下进行的，因此整个运算量也大大降低。

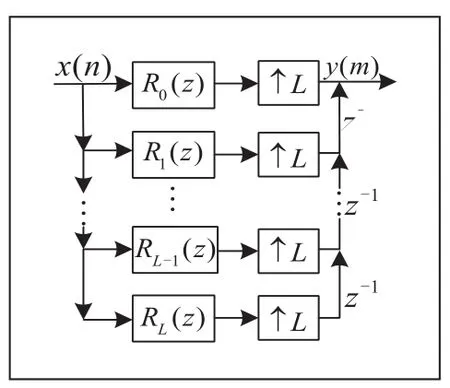
图2 内插滤波器的基本结构图

但实际上虽然每一相的滤波器都在工作，但是实际上在某一时刻，输出的数据只是某一相滤波器的输出数据[5]。这也意味着，在某一时刻，只需要其中的某一相滤波器进行工作，其它相的滤波器可以不工作，那么可以去掉不必要的一些相的滤波器，通过重载滤波器系数的方法来降低来由于P过大导致的硬件资源消耗过多的问题。

图3为本文设计的内插滤波器的改进结构图。在图3中，Ei(z)是经过多相分解后的L相滤波器组，其中i=0 ,1,...,L,这些滤波器系数是被存放在寄存器中的。为了避免出现得到暂态数据的问题，在图2中使用了两相滤波器解决。例如，ER1(z)滤波器中装载的是E0(z)滤波器的系数，ER2(z)滤波器中装载的是E1(z)滤波器的系数，两者是在同时工作，此时，y(m)选择的数据是ER1(z)滤波后的输出数据，在下一时刻，ER1(z)中系数被E2(z)中的系数重载，y(m)选择的数据是ER2(z)滤波后的输出数据。这样就保证最后得到的数据准确的数据。现以一例来验证改进后的内插滤波器的结构较为节省硬件资源。例如，现在需要对一个采样频率为44kHz的信号进行199/200倍升频。通过Matlab中的FDATool工具滤波器参数设计出来的滤波器系数为6869个，在这组系数的后面添加96个零，以便将其分成199相。将滤波器系数进行18位量化后，导入至Quartus Ⅱ中的FIR Complier Ⅱ v13.1核中，最后两种结构的硬件资源消耗对比如表1所示。

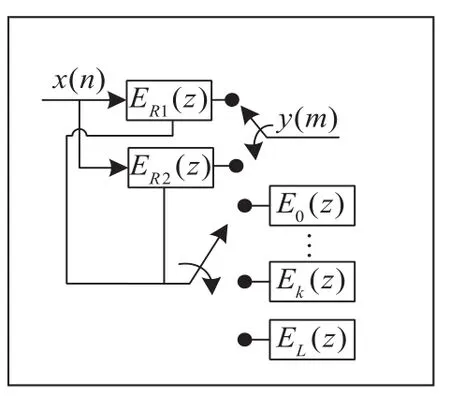
图3 内插滤波器的改进结构图

表1 硬件消耗资源的对比

从表1中可以得到，改进后的内插滤波器的乘法器硬件资源降低至于原来的2/35，而其它资源并没有增加多少，对于FPGA而言，其乘法器资源是非常为珍贵的。因此本文设计的结构可以有效降低硬件资源的消耗。

2 结束语

本文针对P/(P+1)倍和(P+1)/P倍内插多相滤波器的结构进行了改进，主要是通过将多组滤波器系数预先存储在寄存器上，从而避免由于多组滤波器在某时刻的不工作而导致的硬件资源浪费，并通过实际的硬件电路进行了验证，结果表明，改进后的结构相比现有的结构在硬件资源的消耗上有明显的下降，并且性能没有降低，因此该结构可以被广泛应用于数字信号处理中的信号的速率变换中。